相似の利用の解法
Point:相似の利用
商品の値段の比=面積比となるので、
直径の比が \(12:18=2:3\)
これより、面積比が \(2^2:3^2=4:9\)
直径 \(18~{\rm cm}\) のピザの値段 \(x\) 円は、
\(\begin{eqnarray}~~~4:9&=&1000:x
\\[2pt]~~~x&=&2250
\end{eqnarray}\)
よって、\(2250\) 円となる。
あるピザの値段はピザの面積に比例して、直径 \(12~{\rm cm}\) のピザが \(1000\) 円のとき、直径 \(18~{\rm cm}\) のピザの値段の求め方は、
商品の値段の比=面積比となるので、
直径の比が \(12:18=2:3\)
これより、面積比が \(2^2:3^2=4:9\)
直径 \(18~{\rm cm}\) のピザの値段 \(x\) 円は、
\(\begin{eqnarray}~~~4:9&=&1000:x
\\[2pt]~~~x&=&2250
\end{eqnarray}\)
よって、\(2250\) 円となる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:相似の利用
問題解説(1)
問題
\({\small (1)}~\)あるピザの値段は、ピザの面積に比例する。
直径 \(16~{\rm cm}\) のSサイズのピザが \(1200\) 円のとき、
① 直径 \(24~{\rm cm}\) のMサイズのピザの値段を求めよ。
② 直径 \(28~{\rm cm}\) のLサイズのピザの値段を求めよ。
次の問いに答えよ。
\({\small (1)}~\)あるピザの値段は、ピザの面積に比例する。
直径 \(16~{\rm cm}\) のSサイズのピザが \(1200\) 円のとき、
① 直径 \(24~{\rm cm}\) のMサイズのピザの値段を求めよ。
② 直径 \(28~{\rm cm}\) のLサイズのピザの値段を求めよ。
① SサイズとMサイズの直径の比が相似比となるので、
\(~~~16:24=2:3\)
面積比は、相似比の2乗に等しいので、
\(~~~2^2:3^2=4:9\)
ピザの値段の比と面積比が等しくなるので、Mサイズのピザの値段を \(a\) 円とすると、
\(\begin{eqnarray}~~~4:9&=&1200:a\\[2pt]~~~4{\, \small \times \,} a&=&9{\, \small \times \,} 1200\\[3pt]~~~\frac{\,4a\,}{\,4\,}&=&\frac{\,9{\, \small \times \,} 1200\,}{\,4\,}\\[3pt]~~~a&=&9{\, \small \times \,} 300\\[2pt]~~~a&=&2700\end{eqnarray}\)
したがって、Mサイズのピザは \(2700\) 円となる
② SサイズとLサイズの直径の比が相似比となるので、
\(~~~16:28=4:7\)
面積比は、相似比の2乗に等しいので、
\(~~~4^2:7^2=16:49\)
ピザの値段の比と面積比が等しくなるので、Lサイズのピザの値段を \(b\) 円とすると、
\(\begin{eqnarray}~~~16:49&=&1200:b\\[2pt]~~~16{\, \small \times \,} b&=&49{\, \small \times \,} 1200\\[3pt]~~~\frac{\,16b\,}{\,16\,}&=&\frac{\,49{\, \small \times \,} 1200\,}{\,16\,}\\[3pt]~~~b&=&49{\, \small \times \,} 75\\[2pt]~~~b&=&3675\end{eqnarray}\)
したがって、Lサイズのピザは \(3675\) 円となる
問題解説(2)
問題
\({\small (2)}~\)次の図のように、高さ \(10~{\rm cm}\) の円すいの容器に、高さ \(6~{\rm cm}\) まで水が入っている。容器と水の入った部分は相似である。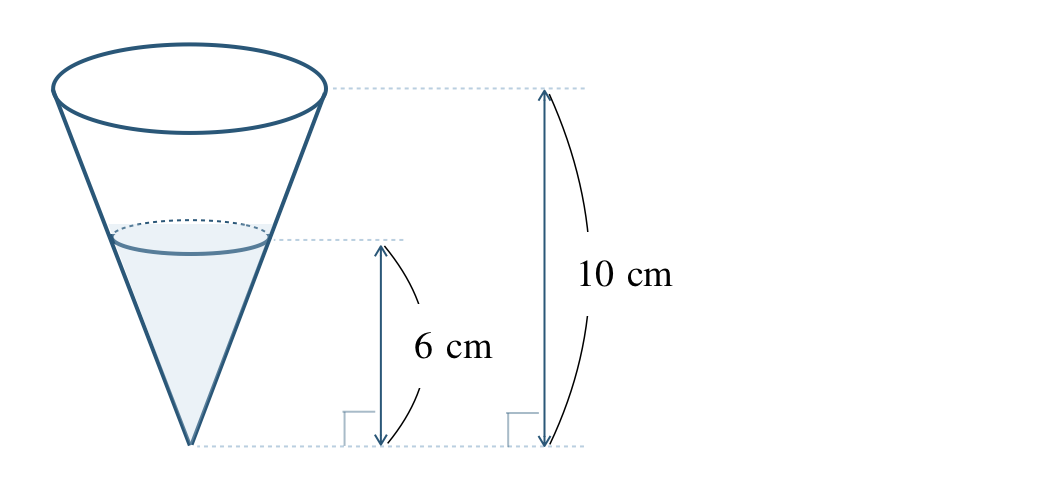
次の問いに答えよ。
\({\small (2)}~\)次の図のように、高さ \(10~{\rm cm}\) の円すいの容器に、高さ \(6~{\rm cm}\) まで水が入っている。容器と水の入った部分は相似である。

① 容器と水の入った部分の相似比を求めよ。
② 容器が容積 \(1000~{\rm cm}^3\) のとき、入っている水の体積を求めよ。
① 容器と水の入った部分の高さの比が相似比となるので、
\(~~~10:6=5:3\)
したがって、相似比は \(5:3\) となる
②
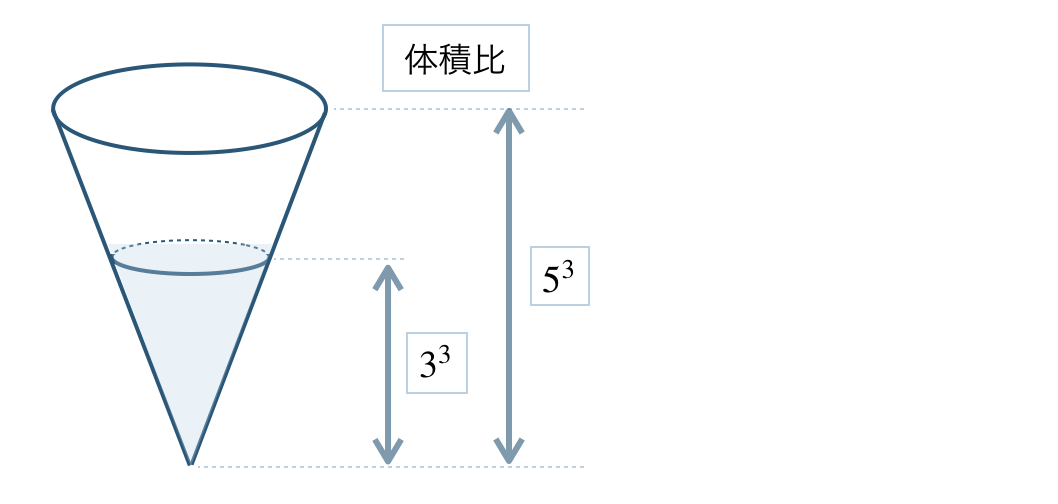
体積比は、相似比の3乗に等しいので、
\(~~~5^3:3^3=125:27\)
容器の容積が \(1000~{\rm cm}^3\) で水の体積を \(x~{\rm cm}^3\) とすると、
\(\begin{eqnarray}~~~125:27&=&1000:x\\[2pt]~~~125{\, \small \times \,} x&=&27{\, \small \times \,}1000\\[3pt]~~~\frac{\,125x\,}{\,125\,}&=&\frac{\,27{\, \small \times \,}1000\,}{\,125\,}\\[3pt]~~~x&=&27{\, \small \times \,}8\\[2pt]~~~x&=&216\end{eqnarray}\)
したがって、水の体積は \(216~{\rm cm}^2\) となる

【問題一覧】中3|相似な図形
このページは「中学数学3 相似な図形」の問題一覧ページとなります。解説の見たい単元名がわからないとき...


