縮図の利用

Point：縮図の利用

■ 縮図の利用

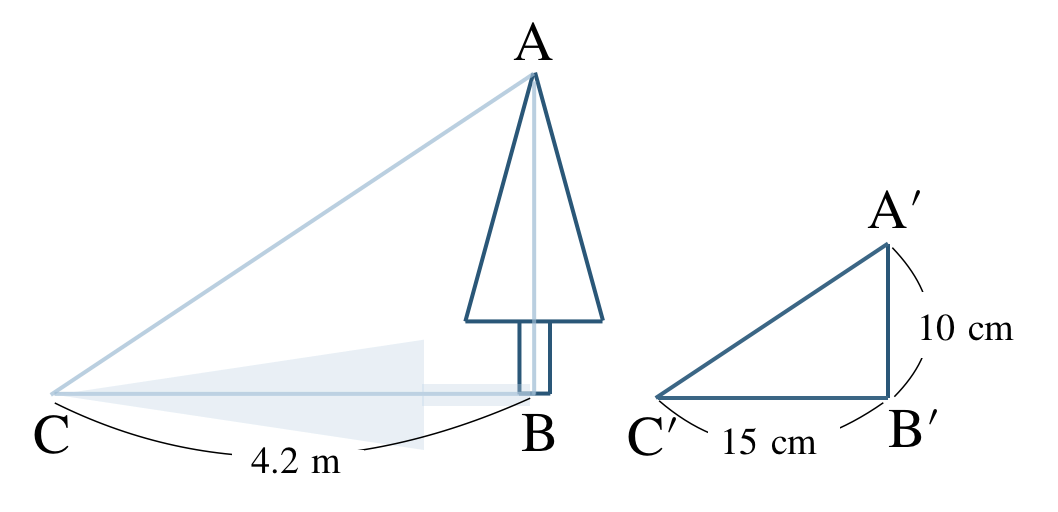
高さ \({\rm AB}~{\rm m}\) の木と、長さが \({\rm BC}=4.2~{\rm m}\) の木の影について、
\(\triangle {\rm ABC}\) の縮図が \(\triangle {\rm A’B’C’}\) となるとき、
\(\triangle {\rm ABC}\) と \(\triangle {\rm A’B’C’}\) は相似であるので、

---

　\(\begin{eqnarray}~~~{\rm AB:BC}&=&{\rm A’B’:B’C’}\\[2pt]~~~{\rm AB}:4.2&=&10:15\\[2pt]~~~{\rm AB}&=&2.8~{\rm m}\end{eqnarray}\)

---

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

問題

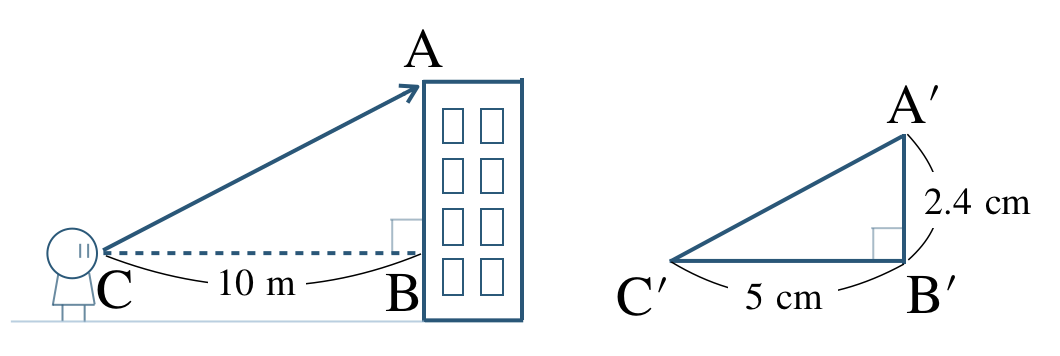
次の問いに答えよ。

---

\({\small (1)}~\)図１はビルから \(10~{\rm m}\) 離れた地点 \({\rm A}\) からビルの上を見上げたもので、図２は図１の \({\large \frac{\,1\,}{\,500\,}}\) の縮図である。目の高さが \(1.5~{\rm m}\) であるとき、ビルの高さを求めよ。

\(\triangle {\rm ABC}\) と \(\triangle {\rm A’B’C’}\) は相似であるので、

---

\(\begin{eqnarray}~~~{\rm AC:BC}&=&{\rm A’C’:B’C’}\\[2pt]~~~{\rm AC}:10&=&2.4:5\\[2pt]~~~{\rm AC}\times5&=&10 \times 2.4\\[2pt]~~~5{\rm AC}&=&24\\[3pt]~~~\frac{\,5{\rm AC}\,}{\,5\,}&=&\frac{\,24\,}{\,5\,}\\[3pt]~~~{\rm AC}&=&4.8\end{eqnarray}\)

---

目の高さが \(1.5~{\rm m}\) であるので、ビルの高さは、

---

\(~~~1.5+4.8=6.3~{\rm m}\)

---

したがって、ビルの高さ \(6.3~{\rm m}\) となる

問題

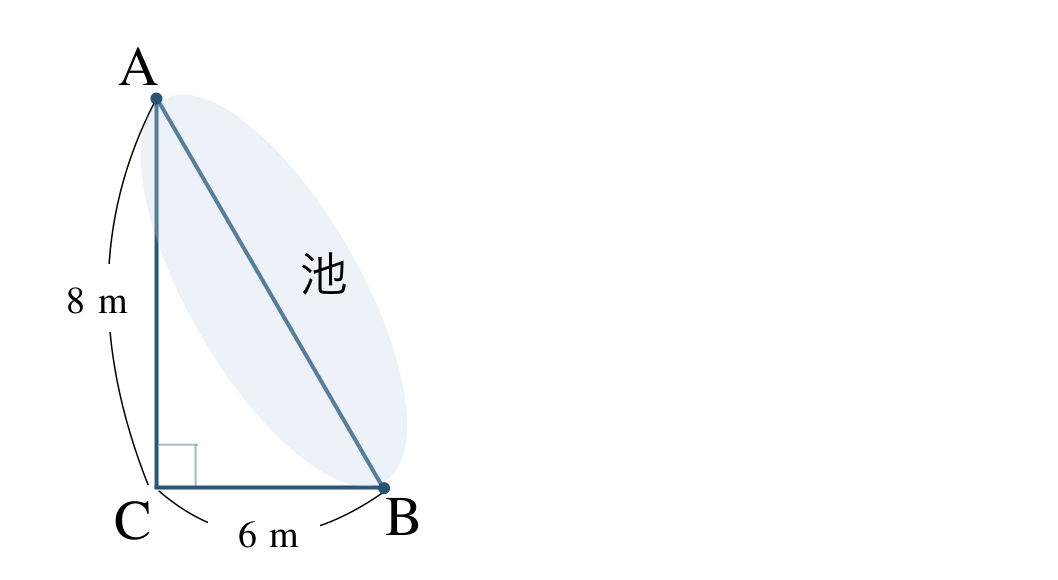
次の問いに答えよ。

---

\({\small (2)}~\)次の図のような池がある。この \(\triangle {\rm ABC}\) の \({\large \frac{\,1\,}{\,200\,}}\) の縮図をかくことで、２点 \({\rm A~,~B}\) の距離を求めよ。

\(\triangle {\rm ABC}\) の \(\begin{split}{ \frac{\,1\,}{\,200\,}}\end{split}\) の縮図を \(\triangle {\rm A’B’C’}\) とすると、
\({\rm AC}=8~{\rm m}=800~{\rm cm}\) より、

---

\(\begin{split}~~~{\rm A’C’}=800\times\frac{\,1\,}{\,200\,}=4~{\rm cm}\end{split}\)

---

\({\rm BC}=6~{\rm m}=600~{\rm cm}\) より、

---

\(\begin{split}~~~{\rm B’C’}=600\times\frac{\,1\,}{\,200\,}=3~{\rm cm}\end{split}\)

---

よって、図をかくと、

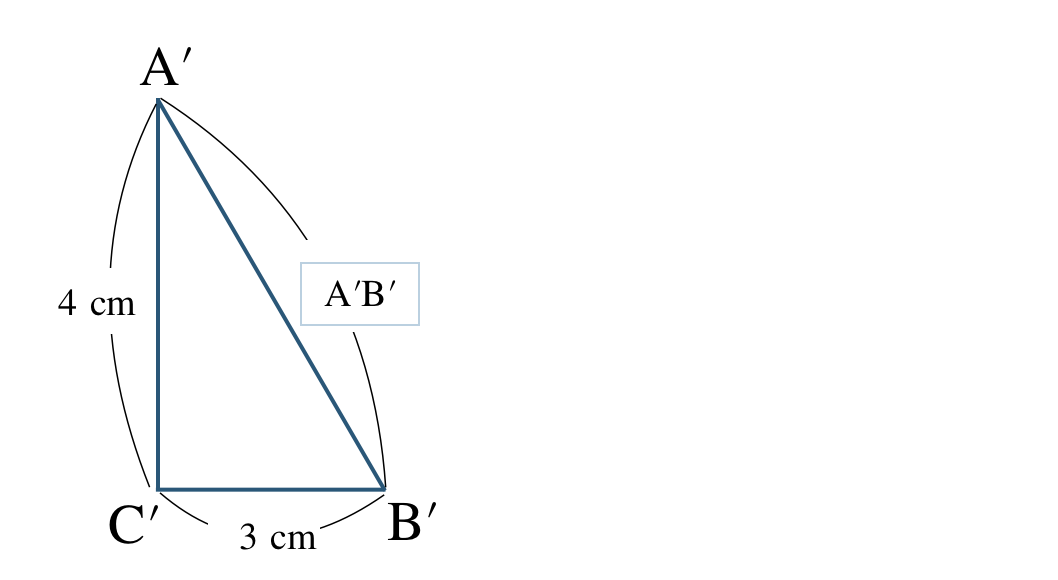
\({\rm A’B’}\) をはかると、

---

\(~~~{\rm A’B’}=5~{\rm cm}\)

---

となる
これより、\({\rm AB}\) の長さは、

---

\(~~~{\rm AB}=5\times200=1000~{\rm cm}=10~{\rm m}\)

---

したがって、２点 \({\rm A~,~B}\) の距離は \(10~{\rm m}\) となる