問題:円周角の定理
次の問いに答えよ。
\({\small (1)}~\)次の角の大きさを求めよ。
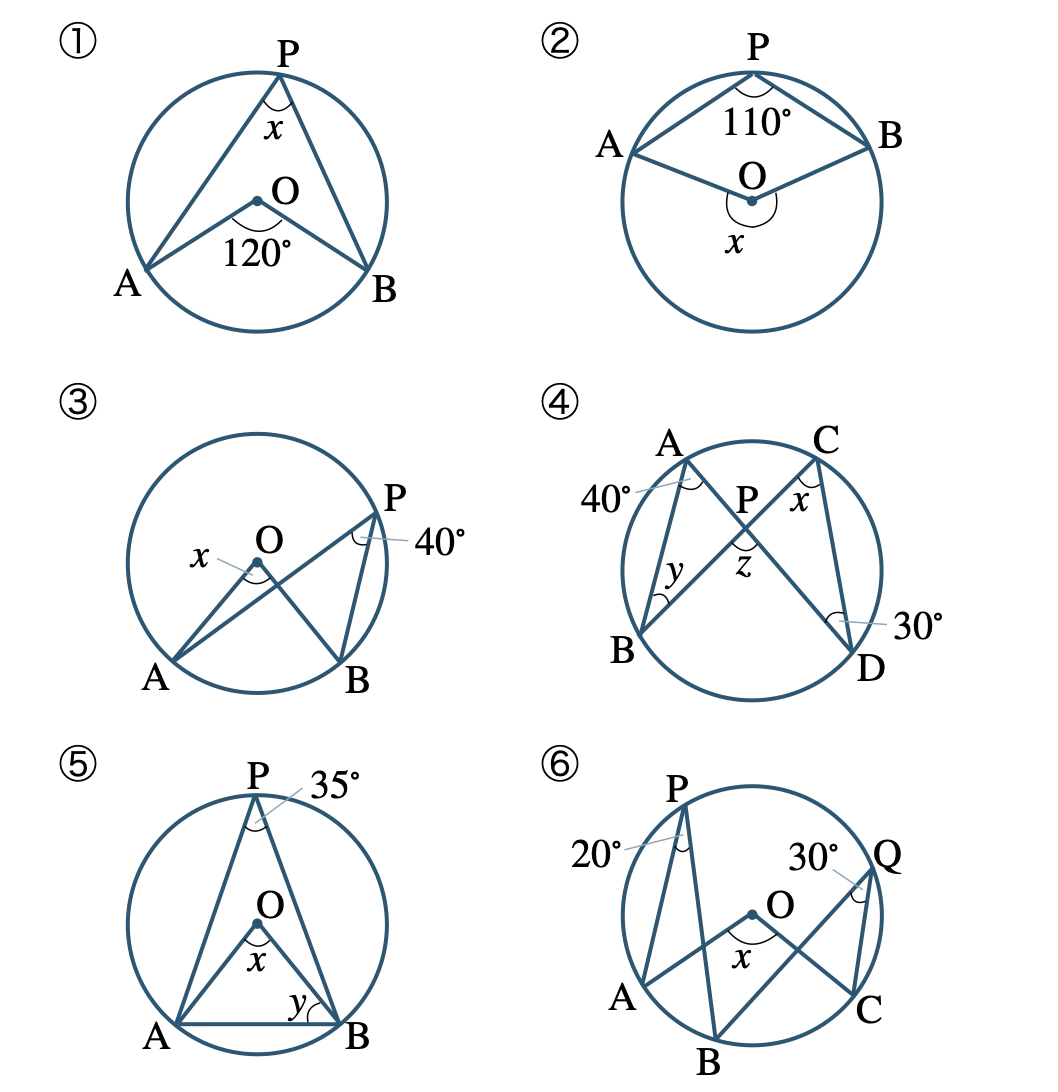
\({\small (2)}~\)次の角の大きさを求めよ。
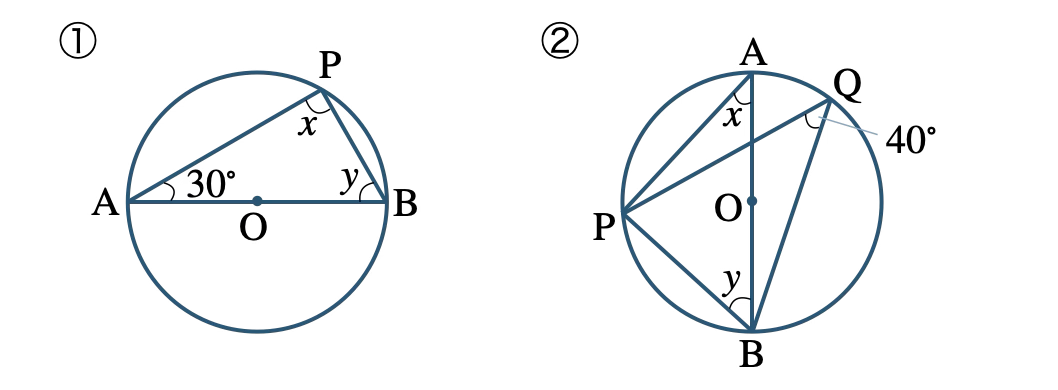
追加の練習問題のページはこちら→
円周角の定理|練習問題100問
解法のPoint
弧 \({\rm AB}\) を \(\overset{\frown}{{\rm AB}}\) で表し、
\(\angle{\rm APB}\)を \(\overset{\frown}{{\rm AB}}\) に対する円周角、
\(\angle{\rm AOB}\)を \(\overset{\frown}{{\rm AB}}\) に対する中心角という。
■ 円周角の定理

【定理1】1つの弧に対する円周角の大きさは、その弧に対する中心角の大きさの半分である。
\(\angle{\rm APB}=\displaystyle \frac{\,1\,}{\,2\,}\angle{\rm AOB}\)
【定理2】同じ弧に対する円周角の大きさは等しい。
\(\angle{\rm APB}=\angle{\rm AP^{\prime}B}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

円周角の定理より、\(\angle{\rm APB}=\displaystyle \frac{\,1\,}{\,2\,}\angle{\rm AOB}\)
また、\(\triangle {\rm OAB}\) は円の半径が等しいので、\({\rm OA=OB}\) の二等辺三角形となる。
よって、底角が等しいので、
\(\angle{\rm OAB}=\angle{\rm OBA}\)
©︎ 2025 教科書より詳しい中学数学 jhs.yorikuwa.com

\({\rm AB}\) が直径のとき、中心角が \(180^\circ\) となるので、
\(\angle{\rm APB}=90^\circ\)
これより、半円の弧に対する円周角は直角となる。
©︎ 2025 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:円周角の定理
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)次の角の大きさを求めよ。
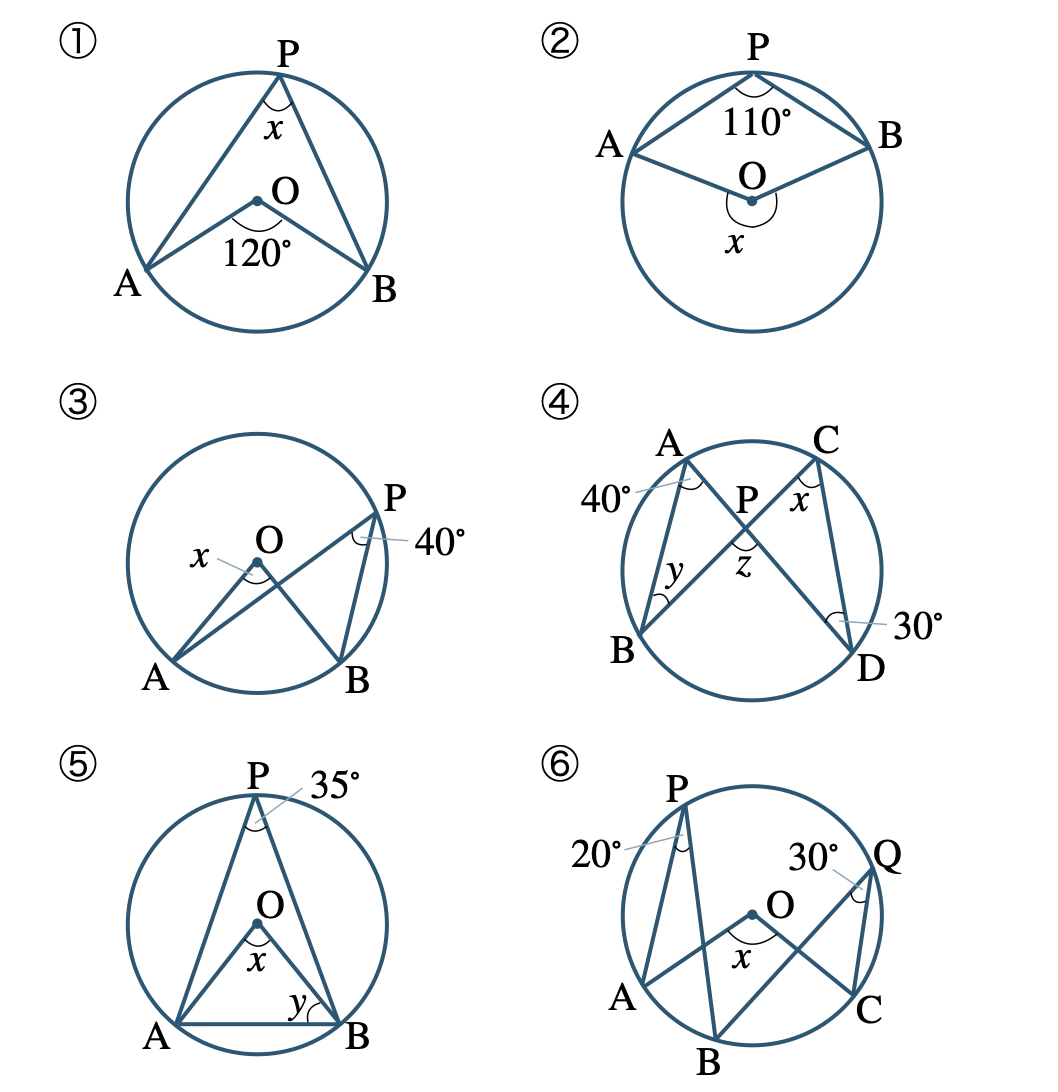

定理1より、\(\overset{\frown}{{\rm AB}}\) に対する円周角は、中心角の半分であるので、
\(x={ \displaystyle \frac{\,1\,}{\,2\,}}{\, \small \times \,}120^\circ=60^\circ\)
したがって、\(x=60^\circ\)

\(\overset{\frown}{{\rm AB}}\) に対する中心角 \(x\) は、円周角 \(110^\circ\) の2倍となるので、
\(x=110^\circ{\, \small \times \,}2=220^\circ\)
したがって、\(x=220^\circ\)

\(\overset{\frown}{{\rm AB}}\) に対する中心角 \(x\) は、円周角 \(40^\circ\) の2倍となるので、
\(x=40^\circ{\, \small \times \,}2=80^\circ\)
したがって、\(x=80^\circ\)
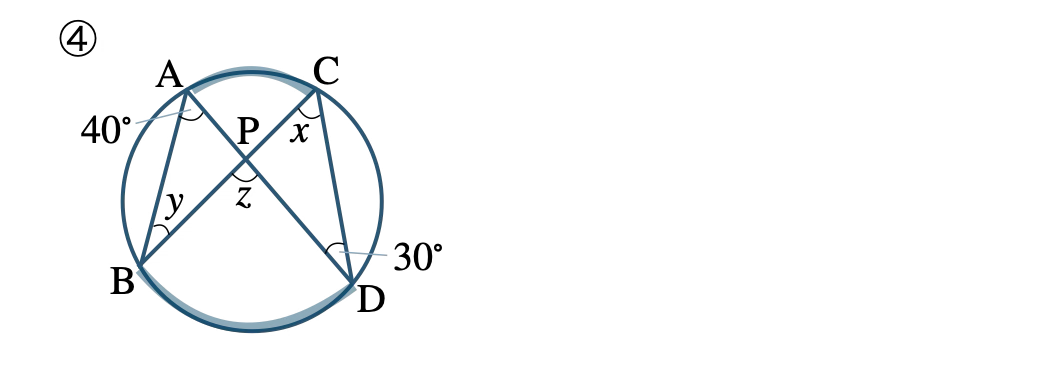
\(\overset{\frown}{{\rm BC}}\) に対する円周角の \(\angle{\rm BAC}~,~\angle{\rm BDC}\) は等しいので、
\(x=40^\circ\)
\(\overset{\frown}{{\rm AD}}\) に対する円周角の \(\angle{\rm ABD}~,~\angle{\rm ACD}\) は等しいので、
\(y=30^\circ\)
\(\angle{\rm BPC}\) は \(\triangle {\rm ABP}\) の外角であるので、隣り合わない2つの内角の和に等しいので、
\(z=40^\circ+30^\circ=70^\circ\)
したがって、\(x=40^\circ~,~y=30^\circ~,~z=70^\circ\)

\(\overset{\frown}{{\rm AB}}\) に対する中心角 \(x\) は、円周角 \(35^\circ\) の2倍となるので、
\(x=35^\circ{\, \small \times \,}2=70^\circ\)
また、\(\triangle {\rm OAB}\) は円の半径が等しいので、\({\rm OA=OB}\) の二等辺三角形となる
よって、底角が等しいので、
\(\angle{\rm OAB}=\angle{\rm OBA}=y\)
三角形の内角の和が \(180^\circ\) より、
\(\begin{eqnarray}~~~70^\circ+y+y&=&180^\circ\\[2pt]~~~2y&=&110^\circ\\[2pt]~~~y&=&55^\circ\end{eqnarray}\)
したがって、\(x=70^\circ~,~y=55^\circ\)

線分 \({\rm OB}\) を引くと、
\(\overset{\frown}{{\rm AB}}\) に対する円周角の定理より、
\(\angle{\rm AOB}=20^\circ{\, \small \times \,}2=40^\circ\)
\(\overset{\frown}{{\rm BC}}\) に対する円周角の定理より、
\(\angle{\rm BOC}=30^\circ{\, \small \times \,}2=60^\circ\)
ここで、\(x=\angle{\rm AOC}=\angle{\rm AOB}+\angle{\rm BOC}\) より、
\(x=40^\circ+60^\circ=100^\circ\)
したがって、\(x=100^\circ\)
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の角の大きさを求めよ。


線分 \({\rm AB}\) が直径より、\(\overset{\frown}{{\rm AB}}\) に対する円周角は直角であるので、
\(x=90^\circ\)
また、三角形の内角の和が \(180^\circ\) より、
\(\begin{eqnarray}~~~90^\circ+30^\circ+y&=&180^\circ\\[2pt]~~~y&=&60^\circ\end{eqnarray}\)
したがって、\(x=90^\circ~,~y=60^\circ\)

\(\overset{\frown}{{\rm PB}}\) に対する円周角の定理より、
\(x=40^\circ\)
線分 \({\rm AB}\) が直径より、\(\overset{\frown}{{\rm AB}}\) に対する円周角は直角であるので、
\(\angle {\rm APB}=90^\circ\)
\(\triangle {\rm APB}\) の内角の和が \(180^\circ\) より、
\(\begin{eqnarray}~~~90^\circ+40^\circ+y&=&180^\circ\\[2pt]~~~y&=&50^\circ\end{eqnarray}\)
したがって、\(x=40^\circ~,~y=50^\circ\)
追加の練習問題のページはこちら→
円周角の定理|練習問題100問



