円周角の定理の逆の解法
■ 円周角の定理の逆
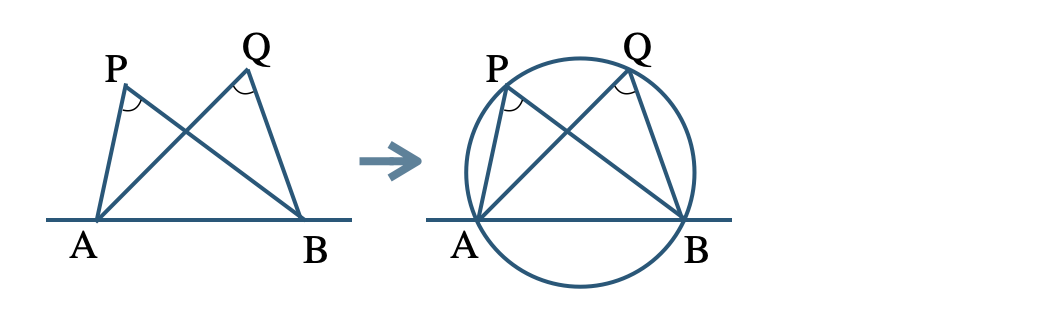
【定理】４点 \({\rm A~,~B~,~P~,~Q}\) について、
２点 \({\rm P~,~Q}\) が直線 \({\rm AB}\) について同じ側にあって、\(\angle{\rm APB}=\angle{\rm AQB}\) ならば、この４点は１つの円周上にある
たとえば、４点 \({\rm A~,~B~,~C~,~D}\) において、
\(\angle{\rm BAC}=\angle{\rm BDC}=30^\circ\) となるとき、
円周角の定理の逆より、４点 \({\rm A~,~B~,~C~,~D}\) が１つの円周上にある
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説：円周角の定理の逆
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)次の①〜④の中で、４点 \({\rm A~,~B~,~C~,~D}\) が１つの円周上にあるものを選べ。
\(\angle{\rm BAC}=\angle{\rm BDC}=35^\circ\) となるので、
円周角の定理の逆より、４点 \({\rm A~,~B~,~C~,~D}\) は１つの円周上にある
※ \(\overset{\frown}{{\rm BC}}\) に対する円周角が等しい
\(\angle{\rm ADB}\neq\angle{\rm ACB}\) であり、
\(\angle{\rm CAD}\neq\angle{\rm CBD}\) であるので、
４点 \({\rm A~,~B~,~C~,~D}\) は１つの円周上にない
\(\triangle {\rm ABC}\) において、内角の和が \(180^\circ\) より、
\(~~~\angle{\rm CBD}=180^\circ-(60^\circ+30^\circ+40^\circ)=50^\circ\)
よって、\(\angle{\rm CAD}=\angle{\rm CBD}=50^\circ\) となるので、
円周角の定理の逆より、４点 \({\rm A~,~B~,~C~,~D}\) は１つの円周上にある
※ \(\overset{\frown}{{\rm CD}}\) に対する円周角が等しい
\(\angle{\rm ABD}=\angle{\rm ACD}=90^\circ\) となるので、
円周角の定理の逆より、４点 \({\rm A~,~B~,~C~,~D}\) は１つの円周上にある
※ \(\overset{\frown}{{\rm AD}}\) に対する円周角が等しい
したがって、答えは ①、③、④ となる
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の図で、角の大きさを求めよ。
① \(\angle{\rm BAC}=\angle{\rm BDC}=50^\circ\) となるので、
円周角の定理の逆より、４点 \({\rm A~,~B~,~C~,~D}\) は１つの円周上にある
これより、\(\overset{\frown}{{\rm AD}}\) に対する円周角の定理より、
\(\begin{eqnarray}~~~\angle{\rm ABD}&=&\angle{\rm ACD}\\[2pt]~~~x&=&30^\circ\end{eqnarray}\)
したがって、\(x=30^\circ\) となる
② \(\angle{\rm ADB}=\angle{\rm ACB}=30^\circ\) となるので、
円周角の定理の逆より、４点 \({\rm A~,~B~,~C~,~D}\) は１つの円周上にある
これより、\(\overset{\frown}{{\rm AD}}\) に対する円周角の定理より、
\(~~~\angle{\rm ABD}=\angle{\rm ACD}=40^\circ\)
\(\overset{\frown}{{\rm CD}}\) に対する円周角の定理より、
\(~~~\angle{\rm CBD}=\angle{\rm CAD}=35^\circ\)
\(x=\angle{\rm ABD}+\angle{\rm CBD}\) より、
\(~~~x=40^\circ+35^\circ=75^\circ\)
したがって、\(x=75^\circ\) となる
問題解説(3)
次の問いに答えよ。
\({\small (3)}~\)次の図で、円 \({\rm O}\) の直径 \({\rm AB}\) と円上の２点 \({\rm C~,~D}\) において、直線 \({\rm AC~,~DB}\) の交点を \({\rm E}\)、直線 \({\rm AD~,~CB}\) の交点を \({\rm F}\) とするとき、４点 \({\rm C~,~D~,~E~,~F}\) は１つの円周上にあることを証明せよ。
・１つの円周上にあることを示すために、\(\overset{\frown}{{\rm FE}}\) に対する円周角が等しいことを示す
・直径 \({\rm AB}\) に対する円周角は \(90^\circ\)
[証明] 直径 \({\rm AB}\) に対する円周角は \(90^\circ\) より、
\(\angle{\rm ACB}=\angle{\rm ADB}=90^\circ\)
これより、外角も \(90^\circ\) となるので、
\(\angle{\rm FCE}=\angle{\rm FDE}=90^\circ\)
したがって、円周角の定理の逆より、４点 \({\rm C~,~D~,~E~,~F}\) は１つの円周上にある [終]
