問題:標本の平均値
問題
\({\small (1)}~\)いちご \(500\) 個から無作為に抽出した \(10\) 個の重さ(g)が次のようになる。
このとき、標本の平均値を答えよ。
\(\begin{eqnarray}~~~&7.1~,~8.3~,~7.8~,~7.8~,~8.9\\[2pt]~~~&7.0~,~7.7~,~8.1~,~6.8~,~8.5\end{eqnarray}\)
\({\small (2)}~\)次の図は、標本の大きさを \(10~,~50\) にして、それぞれ \(30\) 回ずつ無作為に抽出した平均値を箱ひげ図で表したものである。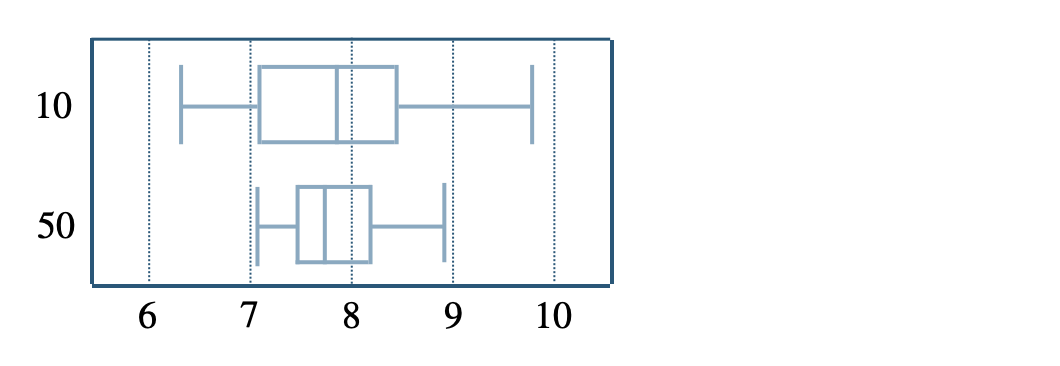
次の問いに答えよ。
\({\small (1)}~\)いちご \(500\) 個から無作為に抽出した \(10\) 個の重さ(g)が次のようになる。
このとき、標本の平均値を答えよ。
\(\begin{eqnarray}~~~&7.1~,~8.3~,~7.8~,~7.8~,~8.9\\[2pt]~~~&7.0~,~7.7~,~8.1~,~6.8~,~8.5\end{eqnarray}\)
\({\small (2)}~\)次の図は、標本の大きさを \(10~,~50\) にして、それぞれ \(30\) 回ずつ無作為に抽出した平均値を箱ひげ図で表したものである。

どのようことが読み取れるか答えよ。
解法のPoint
Point:標本の平均値
また、くり返し標本の平均値を求めたときの値のばらつきは、標本の大きさを大きくすると小さくなり、母集団の平均値に近くなる。
■ 標本の平均値
標本の大きさを決めて、無作為に抽出した値の平均値を「標本の平均値」という。
また、くり返し標本の平均値を求めたときの値のばらつきは、標本の大きさを大きくすると小さくなり、母集団の平均値に近くなる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:標本の平均値
問題解説(1)
問題
\({\small (1)}~\)いちご \(500\) 個から無作為に抽出した \(10\) 個の重さ(g)が次のようになる。
このとき、標本の平均値を答えよ。
\(\begin{eqnarray}~~~&7.1~,~8.3~,~7.8~,~7.8~,~8.9\\[2pt]~~~&7.0~,~7.7~,~8.1~,~6.8~,~8.5\end{eqnarray}\)
次の問いに答えよ。
\({\small (1)}~\)いちご \(500\) 個から無作為に抽出した \(10\) 個の重さ(g)が次のようになる。
このとき、標本の平均値を答えよ。
\(\begin{eqnarray}~~~&7.1~,~8.3~,~7.8~,~7.8~,~8.9\\[2pt]~~~&7.0~,~7.7~,~8.1~,~6.8~,~8.5\end{eqnarray}\)
\(10\) 個の重さの合計は、
\(\begin{eqnarray}&7.1+8.3+7.8+7.8+8.9\\[2pt]&~~~+7.0+7.7+8.1+6.8+8.5=78\end{eqnarray}\)
これより、平均値は、
\(~~~78{\, \small \div \,}10=7.8\)
したがって、答えは \(7.8~{\rm g}\) となる
問題解説(2)
問題
\({\small (2)}~\)次の図は、標本の大きさを \(10~,~50\) にして、それぞれ \(30\) 回ずつ無作為に抽出した平均値を箱ひげ図で表したものである。
次の問いに答えよ。
\({\small (2)}~\)次の図は、標本の大きさを \(10~,~50\) にして、それぞれ \(30\) 回ずつ無作為に抽出した平均値を箱ひげ図で表したものである。

どのようことが読み取れるか答えよ。
標本の大きさ \(10\) の範囲に比べて、標本の大きさ \(50\) の範囲がせまく散らばりが小さい
したがって、標本の大きさを大きくするとばらつきが小さくなり、母集団の平均値に近くなる

【問題一覧】中3|標本調査
このページは「中学数学3 標本調査」の問題一覧ページとなります。解説の見たい単元名がわからないときは...


