度数分布表とヒストグラム

Point：度数分布表

データを整理する区間を「階級」といい、
その区間の幅を「階級の幅」という。

---

それぞれの階級にふくまれるデータの個数を「度数」といい、この階級と度数を表にまとめたものを「度数分布表」という。

また、階級の真ん中の値を「階級値」という。

---

たとえば、上の度数分布表で、
　\(3\) 以上 \(6\) 未満の階級の階級値は、

---

\(\begin{split}~~~\frac{\,3+6\,}{\,2\,}=\frac{\,9\,}{\,2\,}=4.5\end{split}\)

---

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

Point：ヒストグラム

度数分布表の階級の幅を横軸に、度数を縦軸にとったグラフを「ヒストグラム」または「柱状グラフ」という。

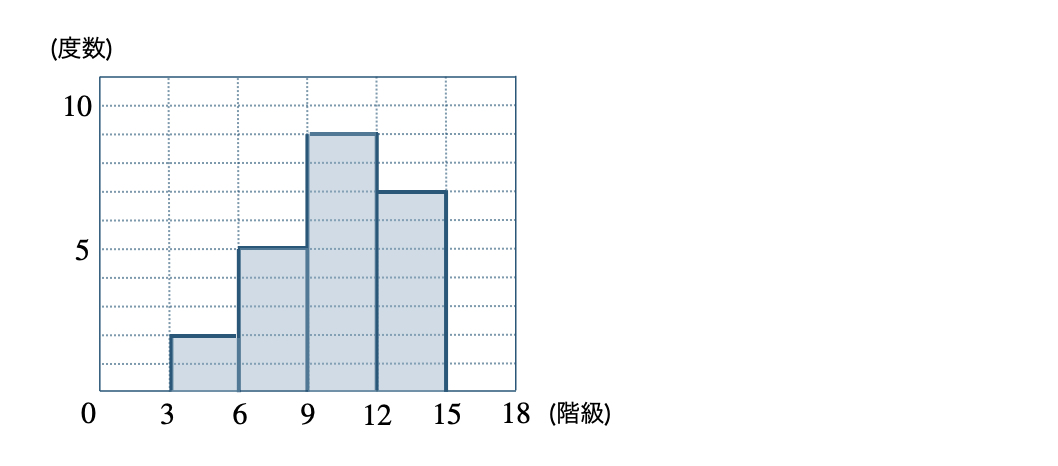
また、ヒストグラムの長方形の上の辺の中点を結んだグラフを「度数折れ線」または「度数分布多角形」という。

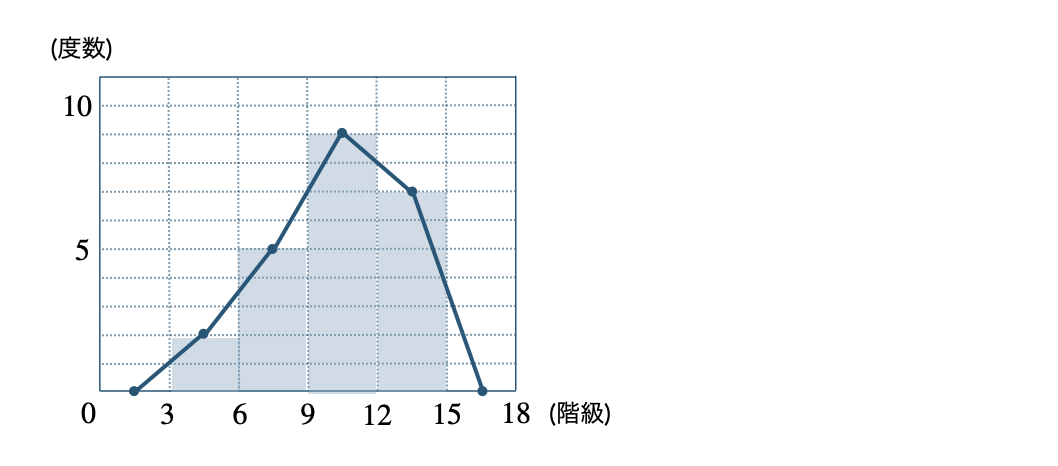
※ 両端では度数が \(0\) となる階級があると考える。

---

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

問題

次のデータは、Ａ市とＢ市の日ごとの最高気温を値の順に並べたものである。次の問いに答えよ。

\({\small (1)}~\)階級を \(20\) ℃から始めて、階級の幅を \(2\) ℃として、それぞれの市の度数分布表を完成させよ。

階級は \(20\) ℃から始めて、階級の幅を \(2\) ℃とするので、
　\(20\) ℃以上〜 \(22\) ℃未満
　\(22\) ℃以上〜 \(24\) ℃未満
　\(24\) ℃以上〜 \(26\) ℃未満
　\(26\) ℃以上〜 \(28\) ℃未満
　\(28\) ℃以上〜 \(30\) ℃未満
　\(30\) ℃以上〜 \(32\) ℃未満
　\(32\) ℃以上〜 \(34\) ℃未満
に分ける
これより、Ａ市のデータを階級で区切ると、

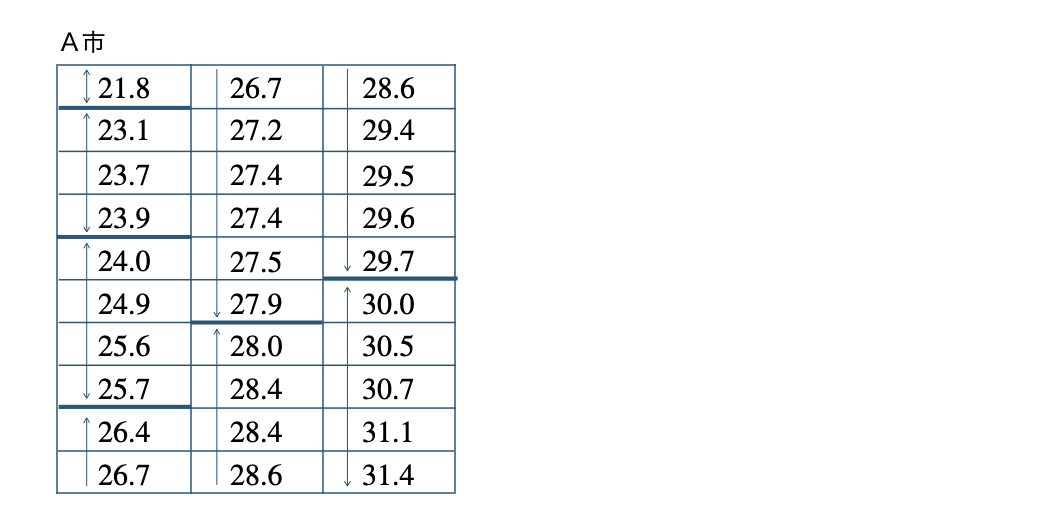
それぞれの階級の度数を求めて、度数分布表を完成させると、

また、Ｂ市のデータを階級で区切ると、

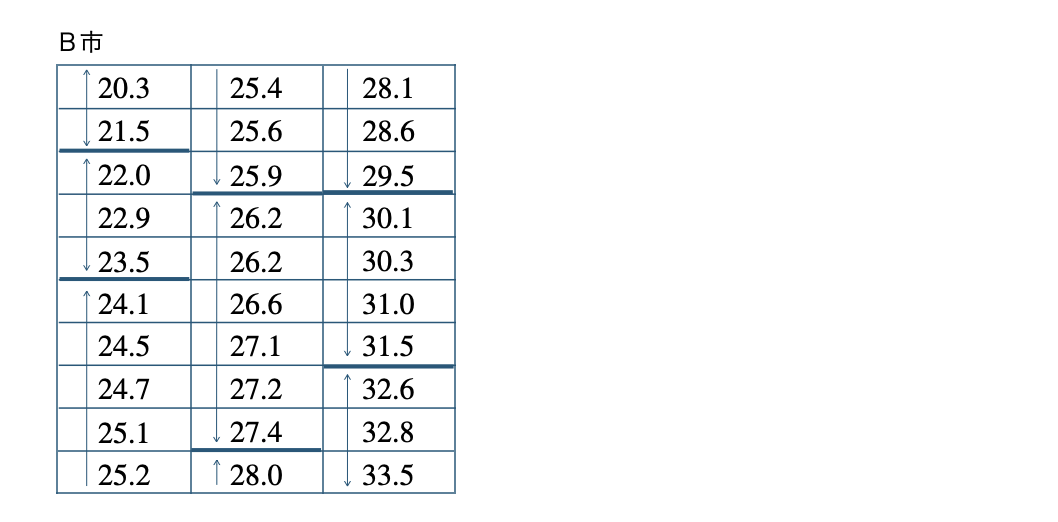
それぞれの階級の度数を求めて、度数分布表を完成させると、

問題

次のデータは、Ａ市とＢ市の日ごとの最高気温を値の順に並べたものである。次の問いに答えよ。

\({\small (2)}~\)それぞれの市のヒストグラムをかけ。

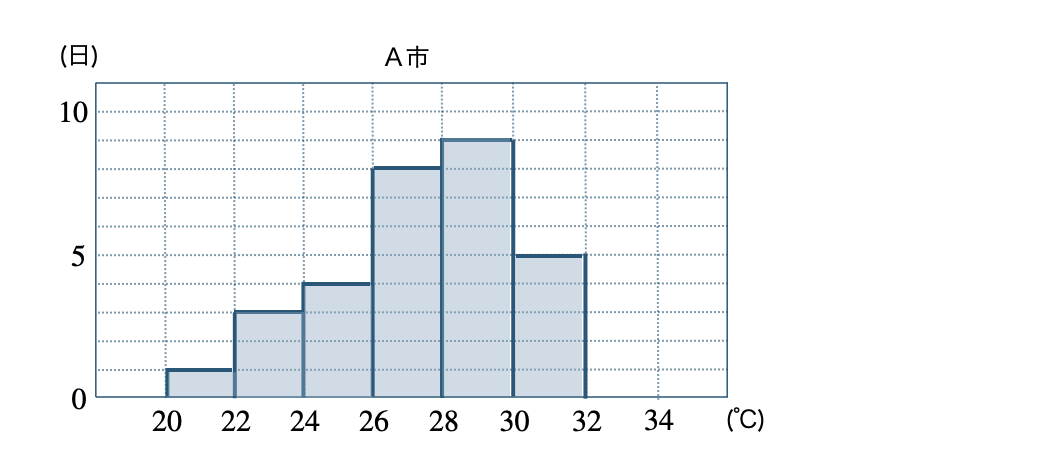
Ａ市の度数分布表は、

これより、ヒストグラムをかくと、

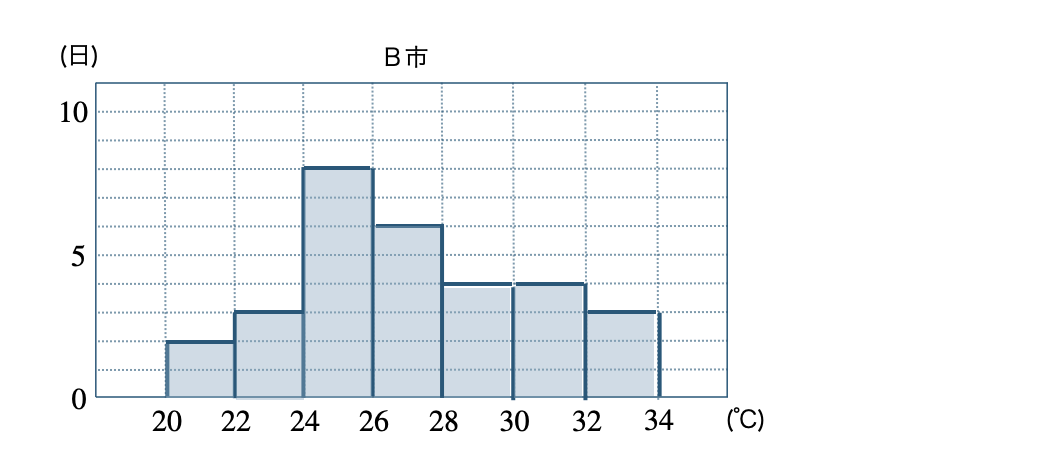
また、Ｂ市の度数分布表は、

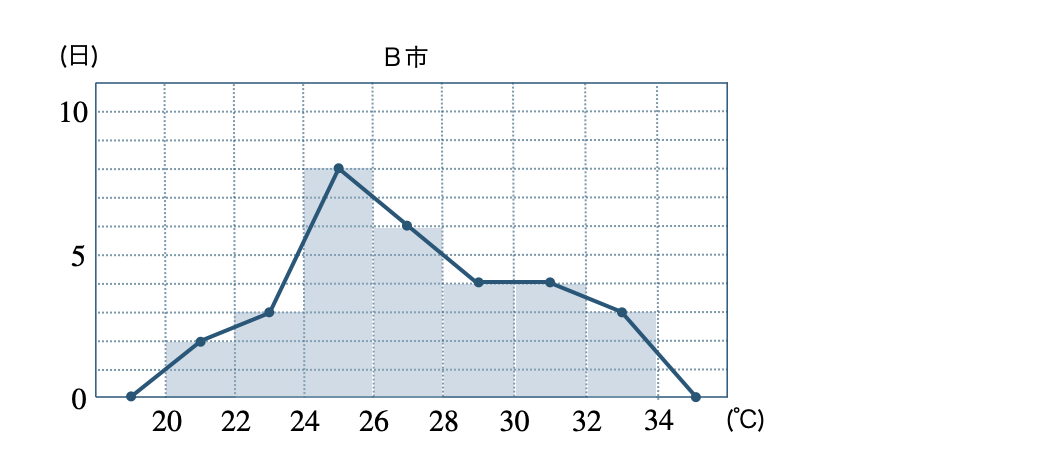
これより、ヒストグラムをかくと、

問題

次のデータは、Ａ市とＢ市の日ごとの最高気温を値の順に並べたものである。次の問いに答えよ。

\({\small (3)}~\)それぞれの市の度数折れ線をかけ。

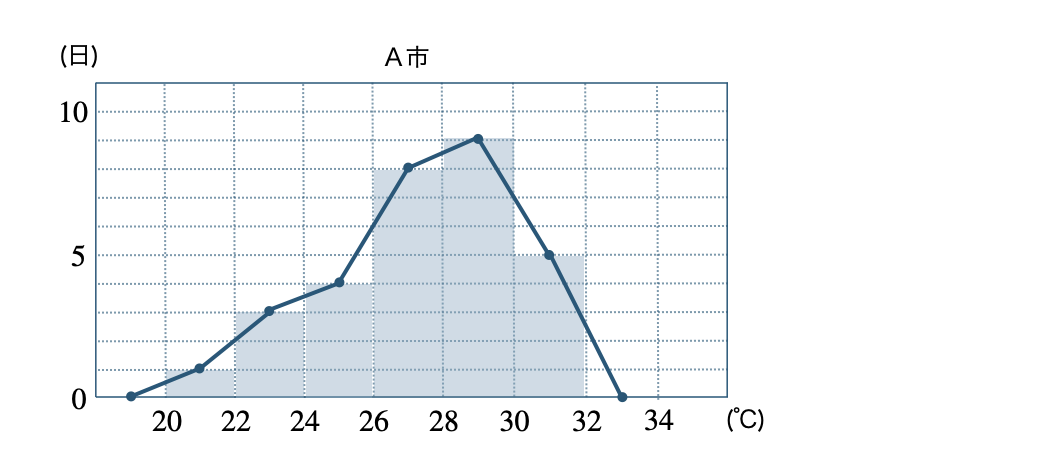
Ａ市のヒストグラムは、

これより、度数折れ線をかくと、

また、Ｂ市のヒストグラムは、

これより、度数折れ線をかくと、