問題:度数分布表と代表値
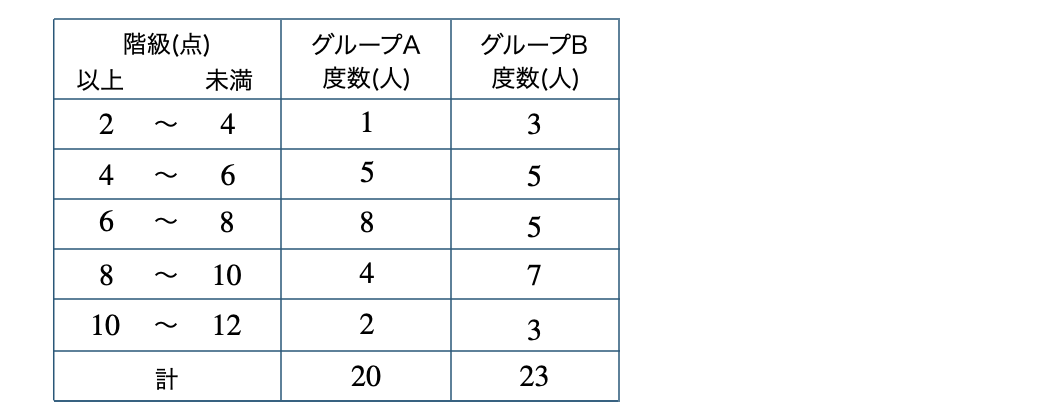
次の表は、\(20\) 人のグループAと \(23\) 人のグループBのあるゲームの得点の度数分布表である。次の問いに答えよ。
\({\small (1)}~\)それぞれのグループの最頻値を求めよ。
\({\small (2)}~\)それぞれのグループの中央値を求めよ。
\({\small (3)}~\)それぞれのグループの平均値を求めよ。
解法のPoint

度数分布表での最頻値は、度数がもっとも多い階級の階級値となる。グループAでは、\(9\) 以上 \(12\) 未満の階級であるので、
\(\begin{split}~~~\frac{\,9+12\,}{\,2\,}=\frac{\,21\,}{\,2\,}=10.5\end{split}\)
度数分布表での中央値は、
グループAでは、奇数個あるので真ん中の値は小さい方から \(12\) 番目の階級値となる。
\(12\) 番目は \(9\) 以上 \(12\) 未満の階級にあるので、
\(\begin{split}~~~\frac{\,9+12\,}{\,2\,}=\frac{\,21\,}{\,2\,}=10.5\end{split}\)
グループBでは、偶数個あるので真ん中2つの \(12\) 番目と \(13\) 番目の平均値となる。
\(12\) 番目と \(13\) 番目はともに \(6\) 以上 \(9\) 未満の階級にあるので、
\(\begin{split}~~~\frac{\,6+9\,}{\,2\,}=\frac{\,15\,}{\,2\,}=7.5\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
度数分布表から平均値を求める方法は、
それぞれのデータの値がわからないので、階級値と度数を使って平均値を求める。

(階級値)×(度数)の和をデータの個数で割ると、
\(\begin{split}~~~\frac{\,9+37.5+94.5+94.5\,}{\,23\,}=10.2\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:度数分布表と代表値
問題解説(1)
次の表は、\(20\) 人のグループAと \(23\) 人のグループBのあるゲームの得点の度数分布表である。次の問いに答えよ。

\({\small (1)}~\)それぞれのグループの最頻値を求めよ。
Aの最頻値は、度数が \(8\) の \(6\) 点以上 \(8\) 点未満の階級である
よって、階級値は、
\(\begin{split}~~~\frac{\,6+8\,}{\,2\,}=\frac{\,14\,}{\,2\,}=7\end{split}\)
Bの最頻値は、度数が \(7\) の \(8\) 点以上 \(10\) 点未満の階級である
よって、階級値は、
\(\begin{split}~~~\frac{\,8+10\,}{\,2\,}=\frac{\,18\,}{\,2\,}=9\end{split}\)
したがって、答えは
Aの最頻値は \(7\) 点
Bの最頻値は \(9\) 点
となる
問題解説(2)
次の表は、\(20\) 人のグループAと \(23\) 人のグループBのあるゲームの得点の度数分布表である。次の問いに答えよ。

\({\small (2)}~\)それぞれのグループの中央値を求めよ。
グループAは偶数個あるので、中央値は \(10\) 人目と \(11\) 人目の真ん中である
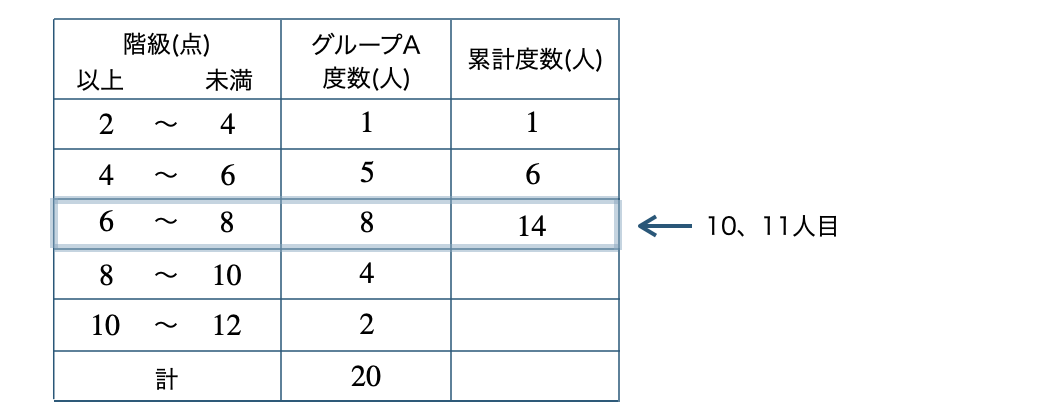
これより、\(10\) 人目も \(11\) 人目も \(6\) 点以上 \(8\) 点未満の階級にいるので、
階級値は、
\(\begin{split}~~~\frac{\,6+8\,}{\,2\,}=\frac{\,14\,}{\,2\,}=7\end{split}\)
グループBは奇数個あるので、中央値は \(12\) 人目である
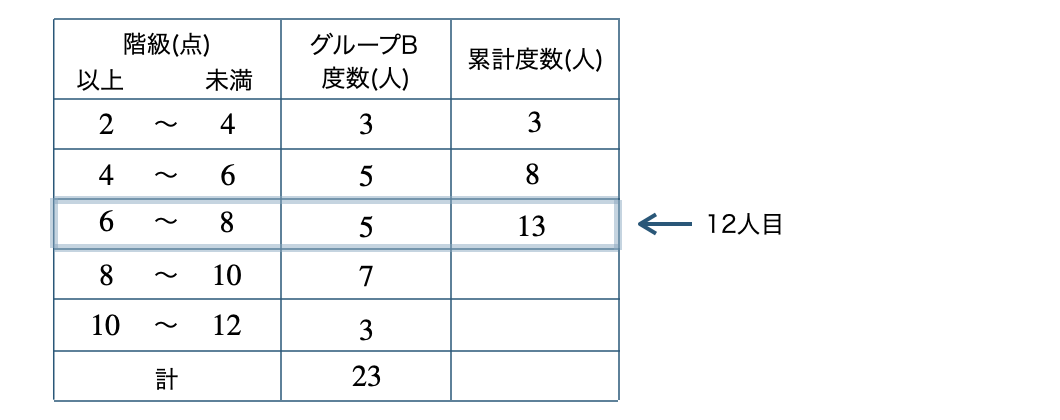
これより、 \(12\) 人目は \(6\) 点以上 \(8\) 点未満の階級にいるので、
階級値は、
\(\begin{split}~~~\frac{\,6+8\,}{\,2\,}=\frac{\,14\,}{\,2\,}=7\end{split}\)
したがって、答えは
Aの中央値は \(7\) 点
Bの中央値は \(7\) 点
となる
問題解説(3)
次の表は、\(20\) 人のグループAと \(23\) 人のグループBのあるゲームの得点の度数分布表である。次の問いに答えよ。

\({\small (3)}~\)それぞれのグループの平均値を求めよ。
グループAの階級値と階級値×度数の値を表にまとめると、

これより、階級値×度数の和を総数 \(20\) で割った値が平均値となるので、
\(\begin{split}&\frac{\,3+25+56+36+22\,}{\,20\,}
\\[3pt]~~=~&\frac{\,142\,}{\,20\,}=7.1
\end{split}\)
グループBの階級値と階級値×度数の値を表にまとめると、

これより、階級値×度数の和を総数 \(23\) で割った値が平均値となるので、
\(\begin{split}&\frac{\,9+25+35+63+33\,}{\,23\,}
\\[2pt]~~=~&\frac{\,165\,}{\,23\,}=7.17\cdots
\end{split}\)
したがって、答えは
Aの平均値は \(7.1\) 点
Bの平均値は約 \(7.2\) 点
となる



