このページでは、「相対度数と累積相対度数」をテストに直結する形で練習できます。各問は[解答を見る]からすぐに答えを確認できます。
- 対象:中学数学(教科書レベル)/授業の復習やテスト前の確認にぴったり
- レベル:基本問題を中心にそろえてあるので、安心して取り組めます
- 使い方:全部を解く必要はなく、理解できたと思えるところまで進めれば大丈夫です
- 利用方法:学校や塾での小テスト、家庭学習のプリントなどにも自由にお使いいただけます
【中学数学】相対度数と累積相対度数の練習問題100問
この問題の解き方の詳細は↓
相対度数と累積相対度数の解法まとめ で確認できます。
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(9\) 未満の割合を求めよ。
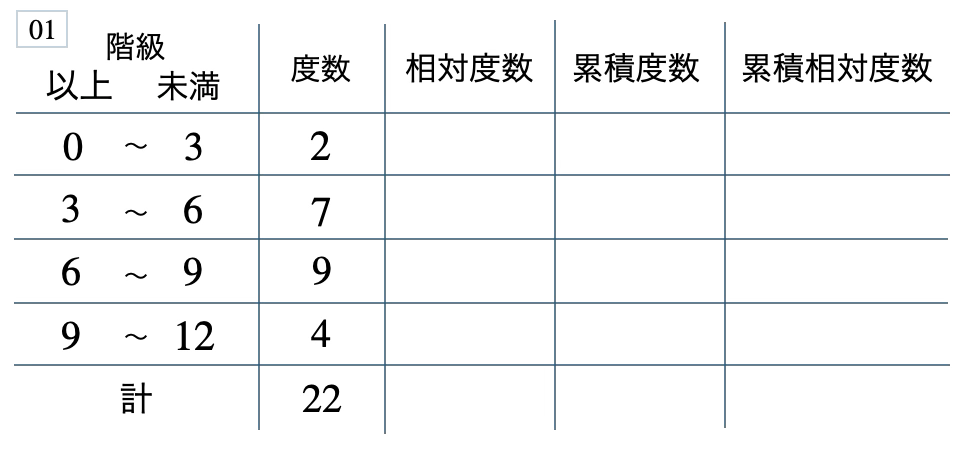
[ 解答を見る ]
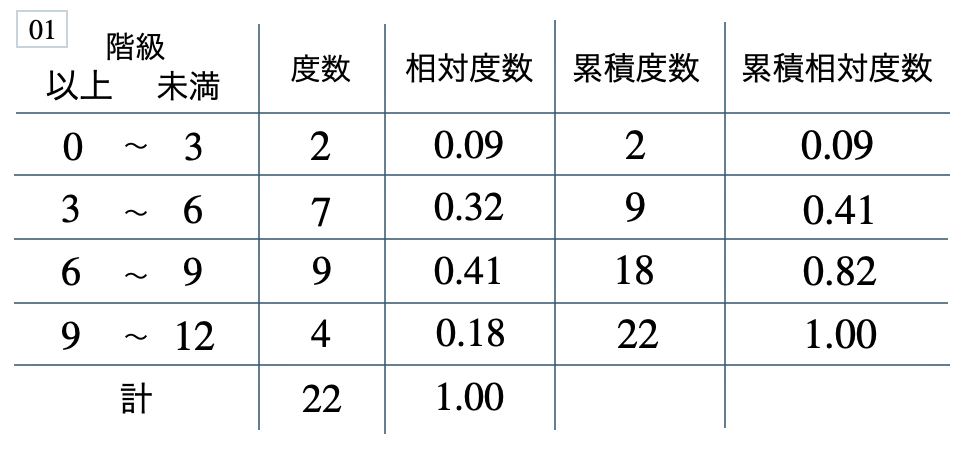
\(41\) %、\(0.82\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(12\) 以上の割合を求めよ。
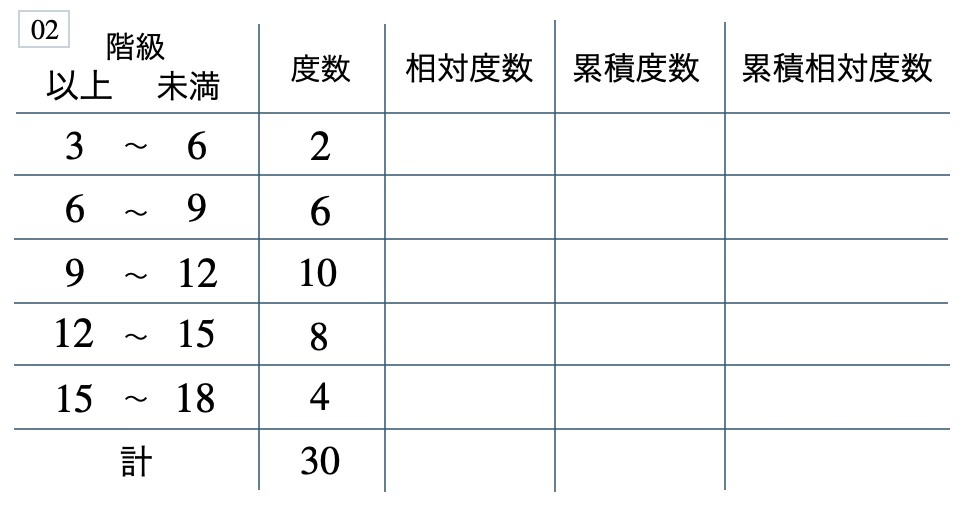
[ 解答を見る ]
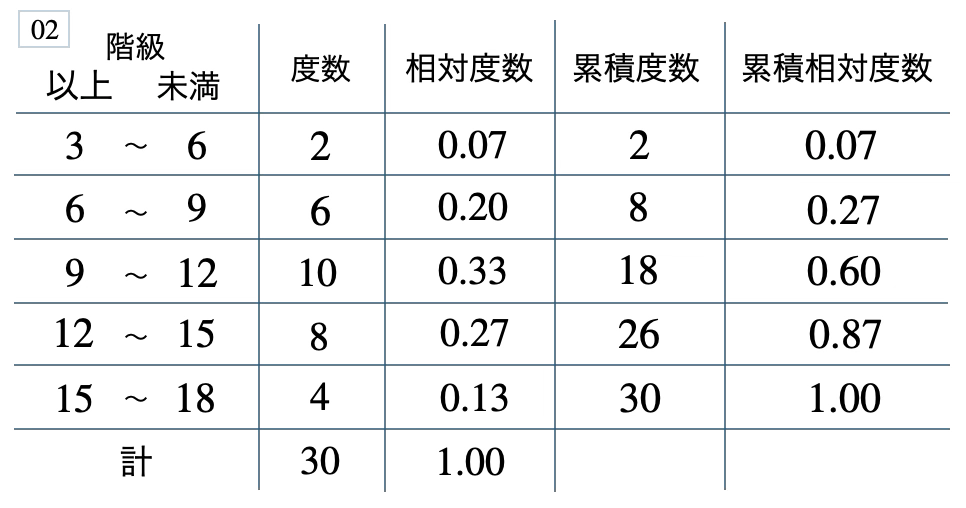
\(33\) %、\(0.40\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(12\) 以上の割合を求めよ。
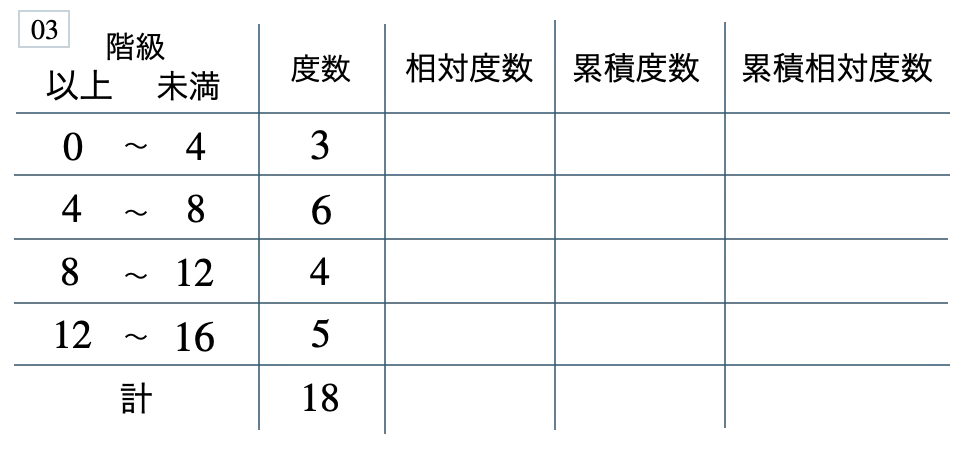
[ 解答を見る ]
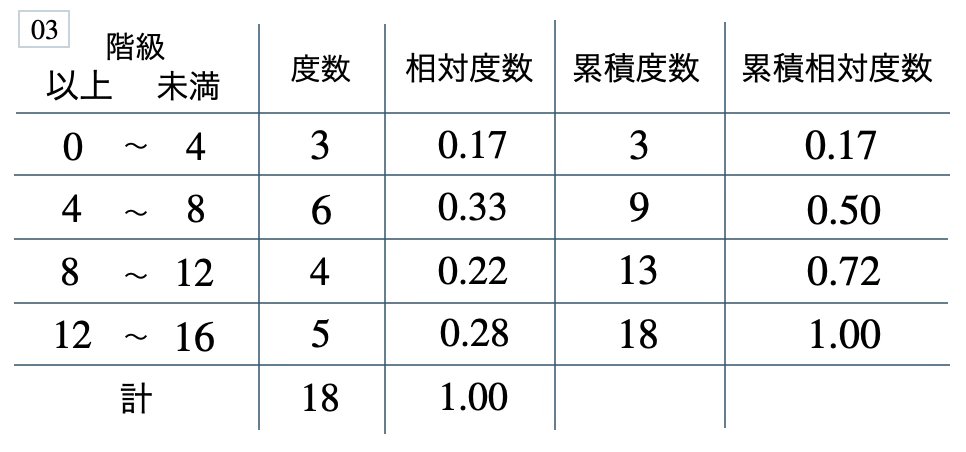
\(33\) %、\(0.28\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(9\) 以上の割合を求めよ。
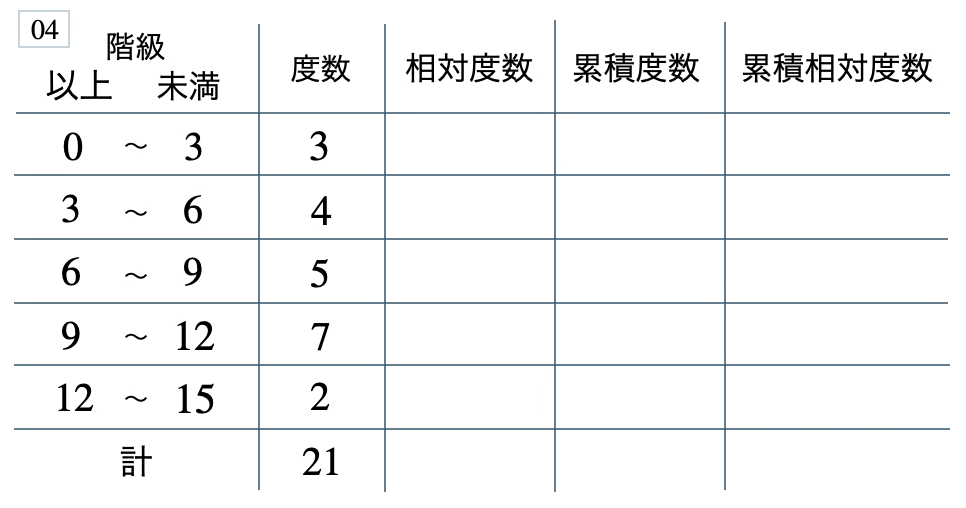
[ 解答を見る ]
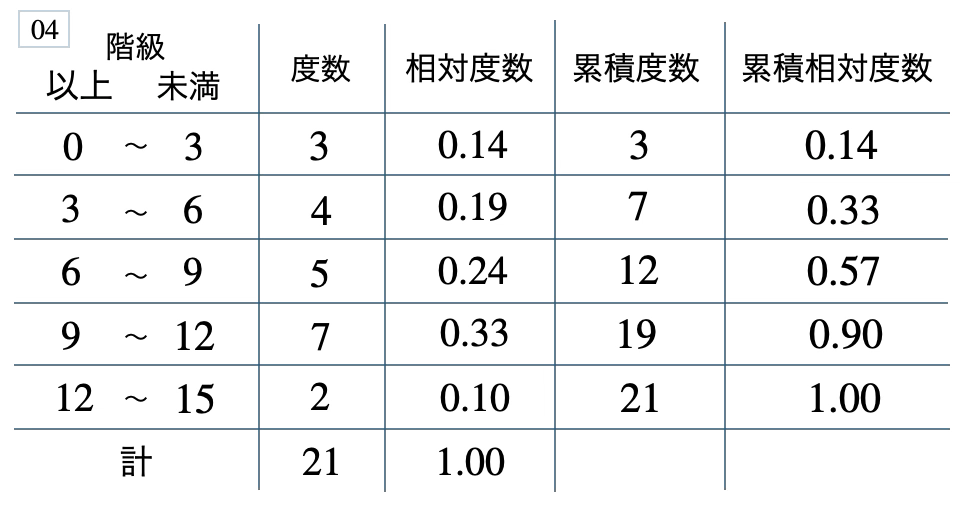
\(33\) %、\(0.43\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(9\) 未満の割合を求めよ。
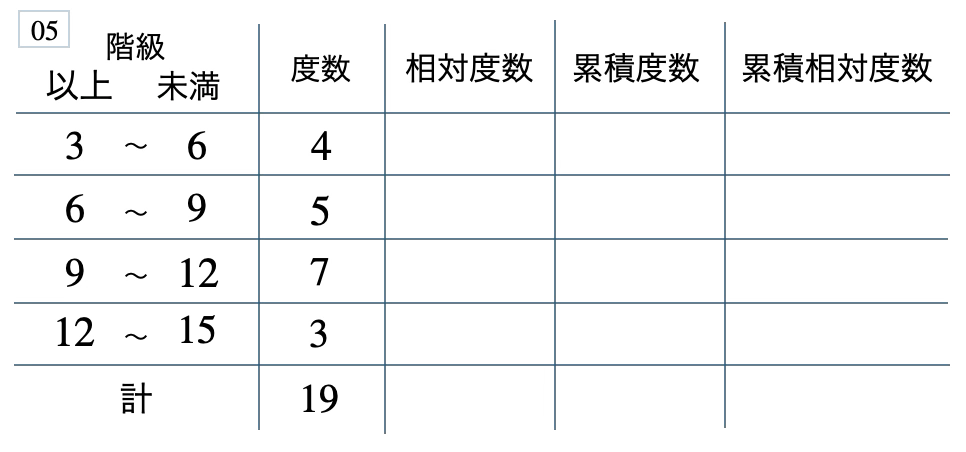
[ 解答を見る ]
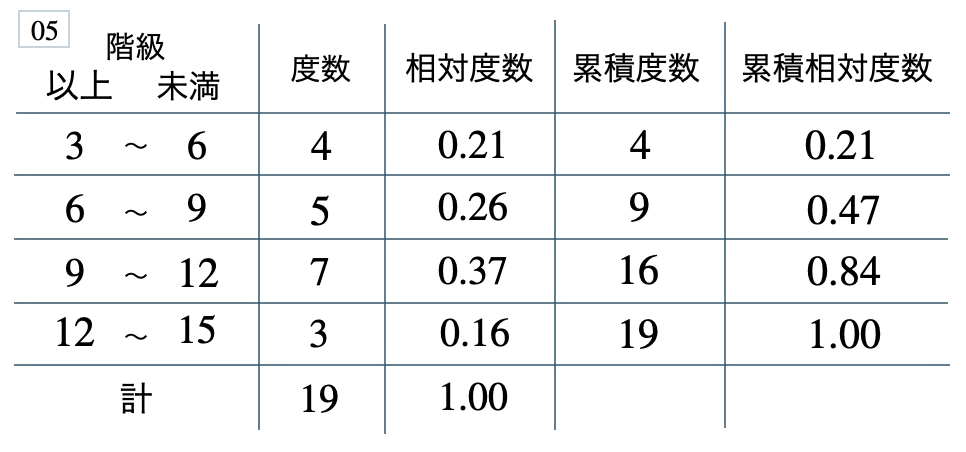
\(37\) %、\(0.47\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(12\) 以上の割合を求めよ。
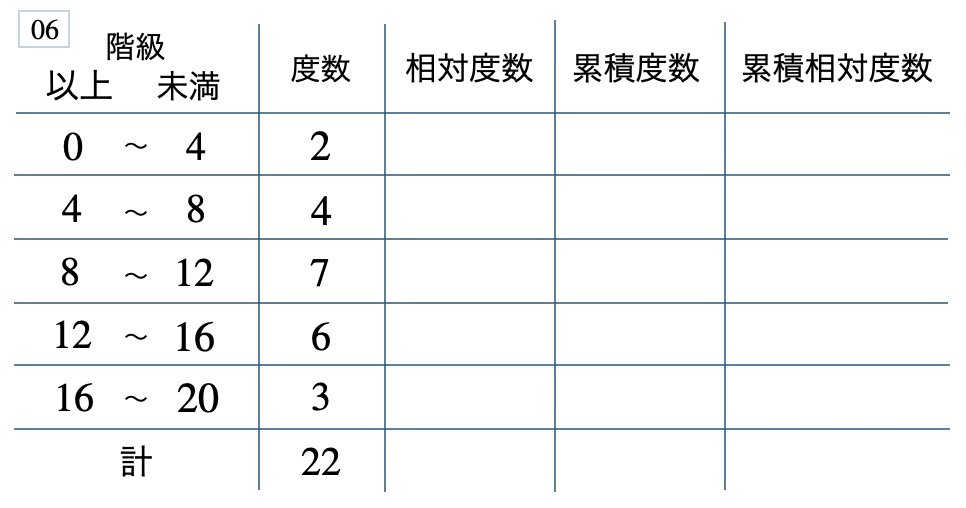
[ 解答を見る ]
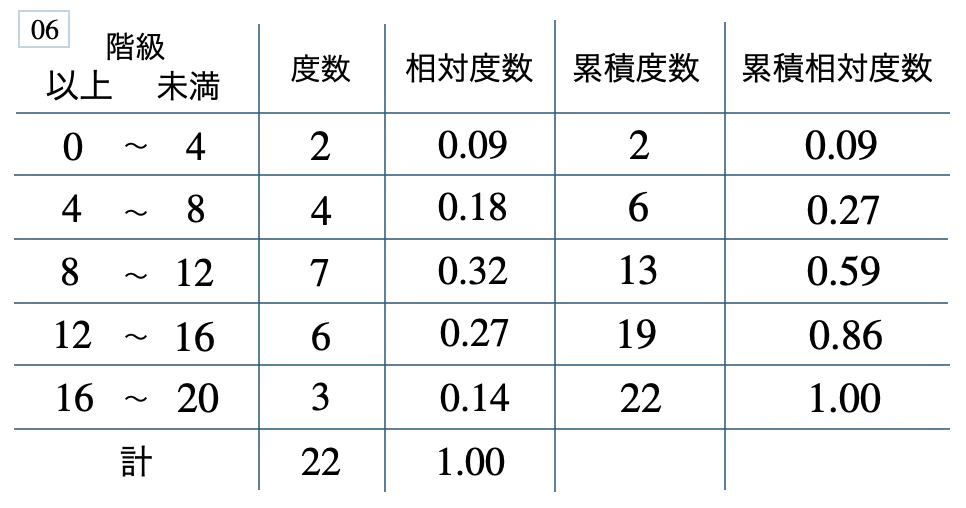
\(32\) %、\(0.41\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(8\) 未満の割合を求めよ。
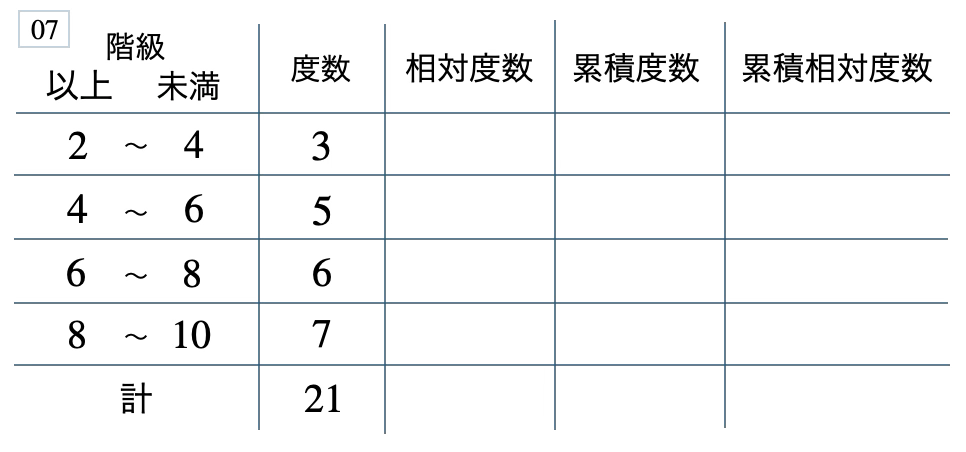
[ 解答を見る ]
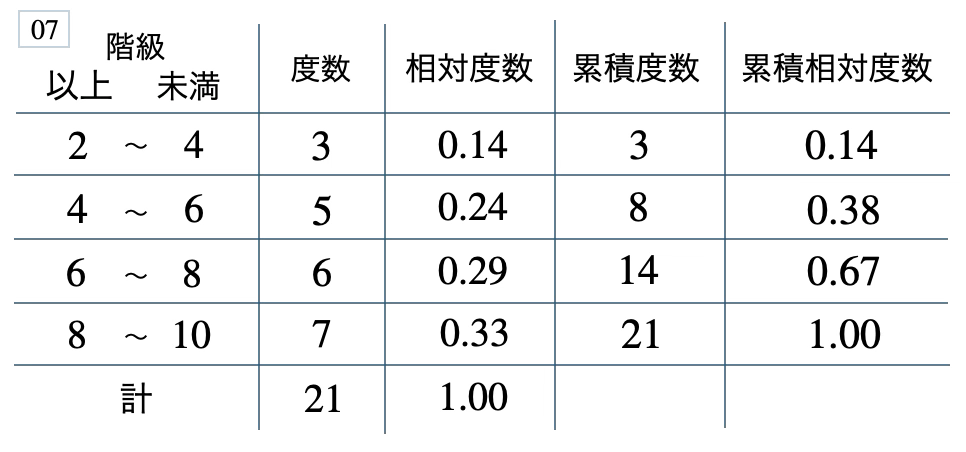
\(33\) %、\(0.67\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(10\) 以上の割合を求めよ。
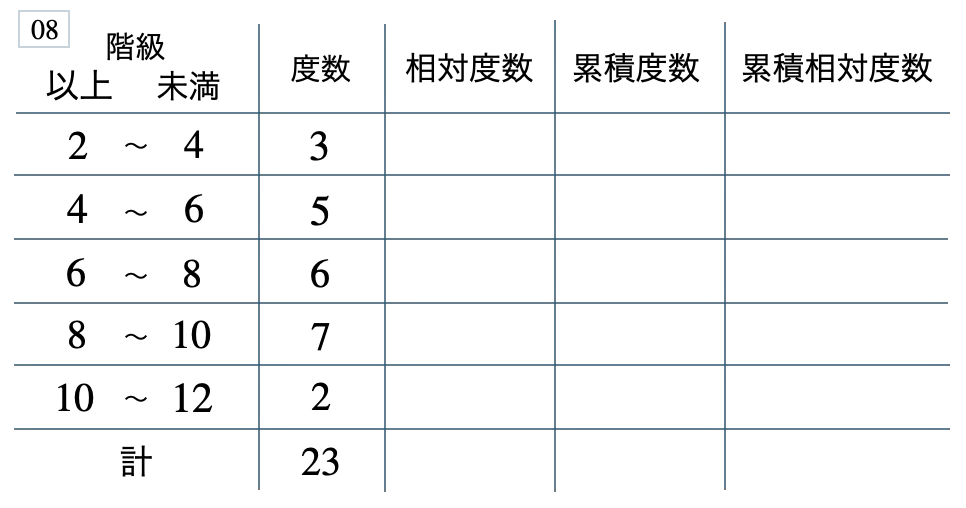
[ 解答を見る ]
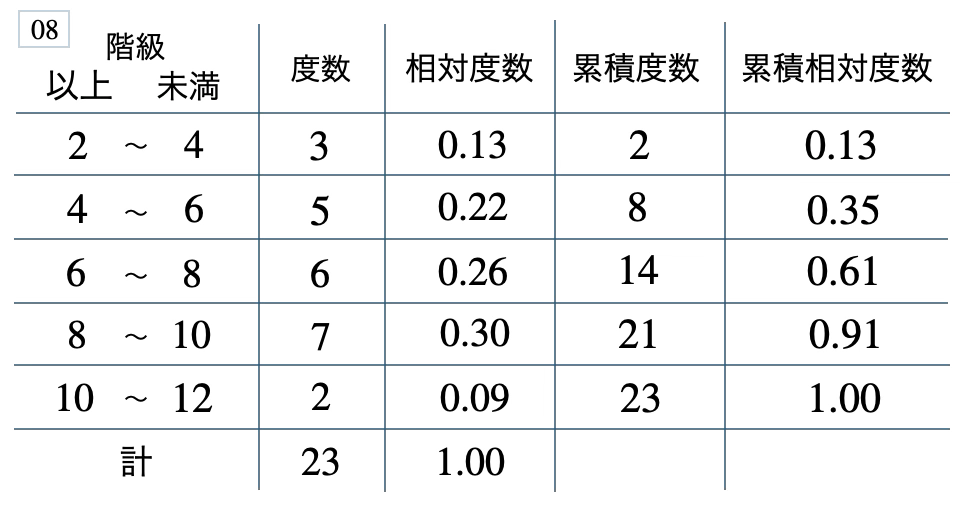
\(30\) %、\(0.09\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(7\) 未満の割合を求めよ。
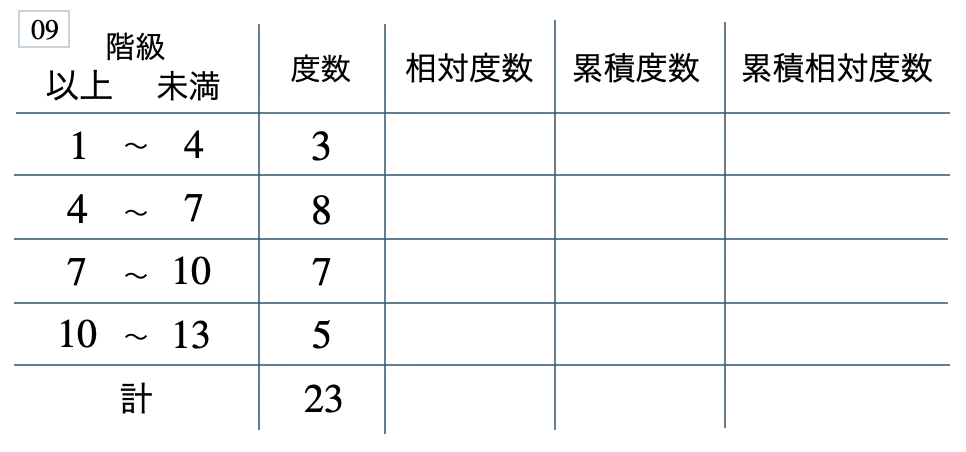
[ 解答を見る ]
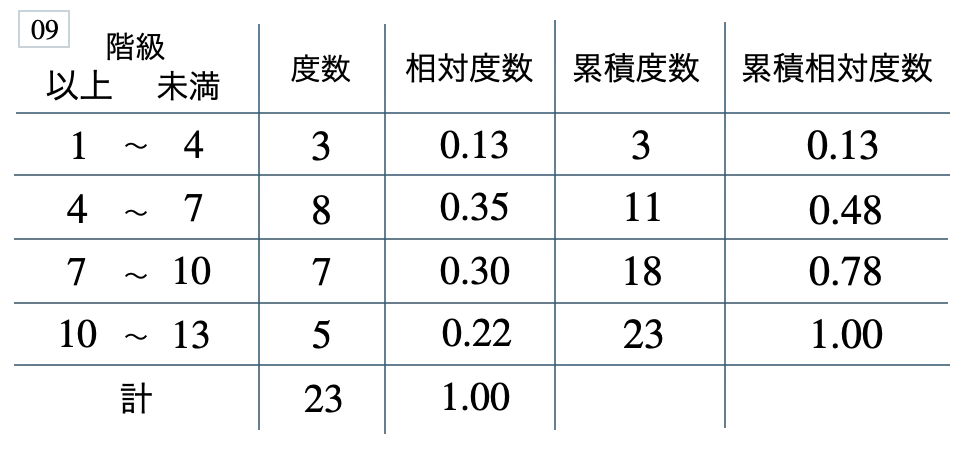
\(35\) %、\(0.48\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(7\) 以上の割合を求めよ。
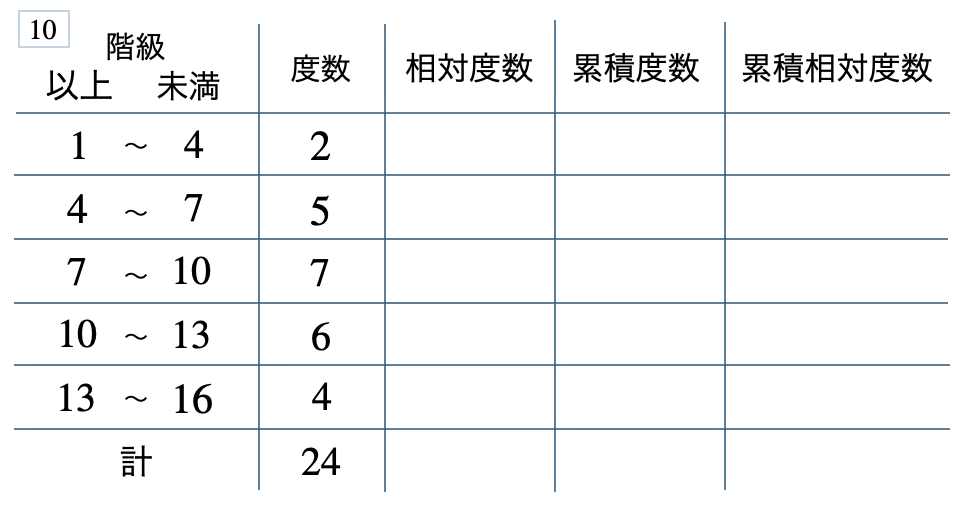
[ 解答を見る ]
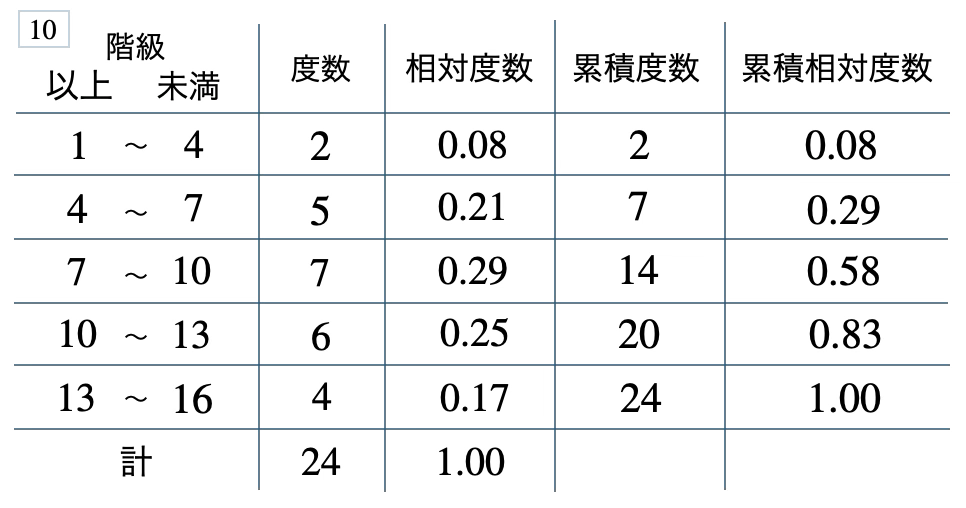
\(29\) %、\(0.71\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(6\) 未満の割合を求めよ。
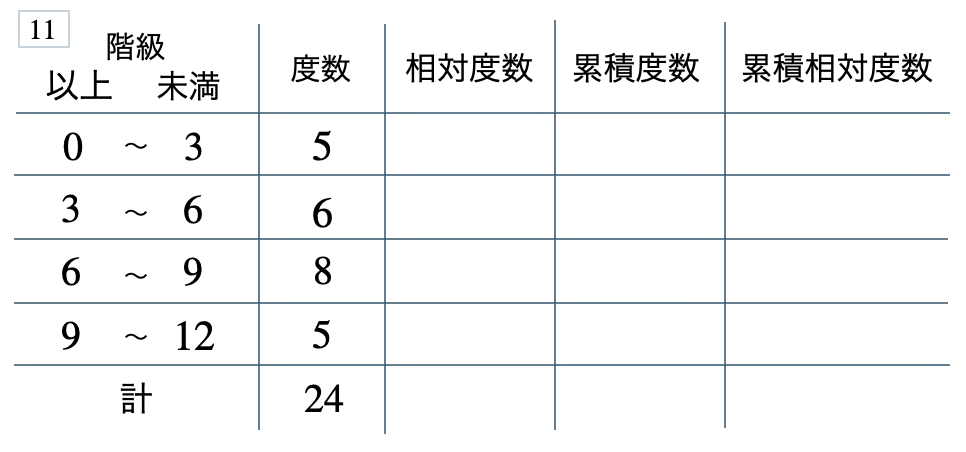
[ 解答を見る ]
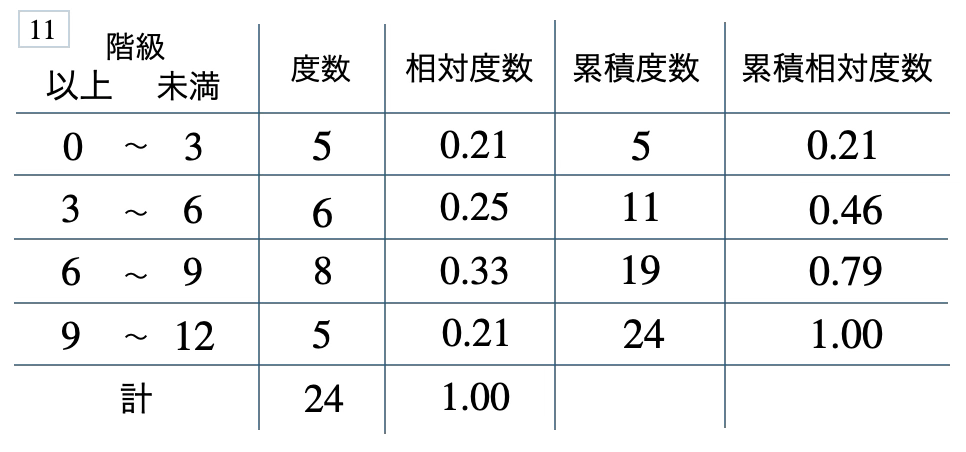
\(33\) %、\(0.46\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(12\) 以上の割合を求めよ。
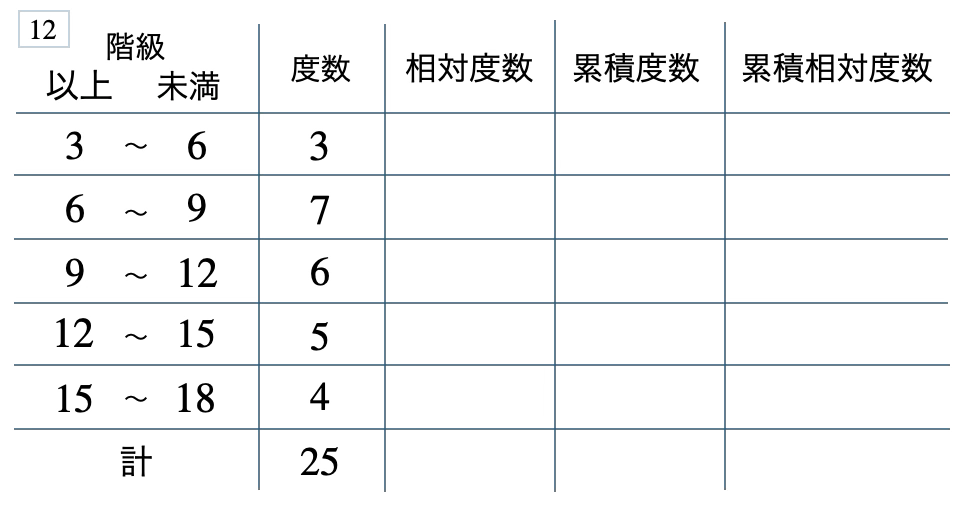
[ 解答を見る ]
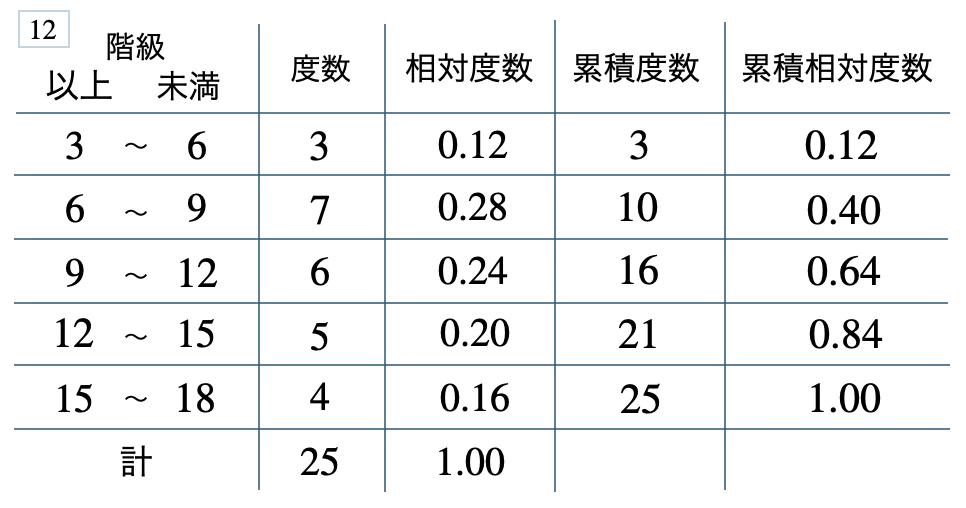
\(28\) %、\(0.36\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(12\) 以上の割合を求めよ。
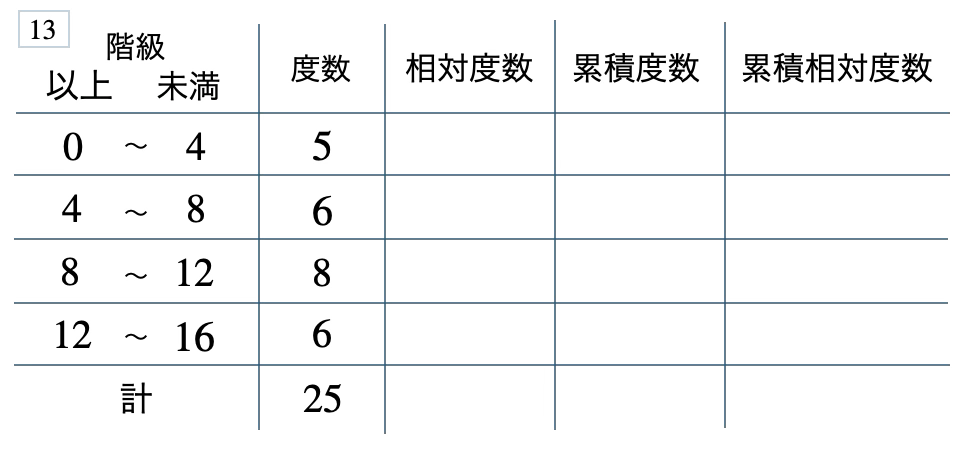
[ 解答を見る ]
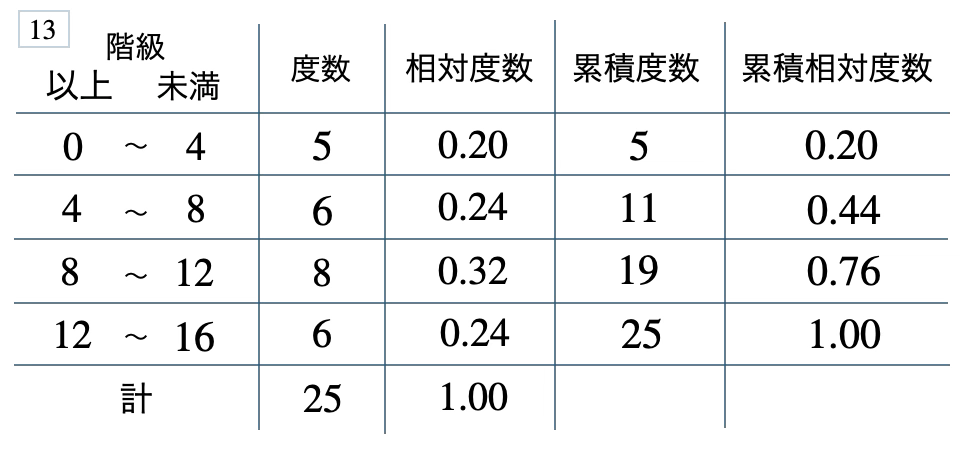
\(32\) %、\(0.24\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(9\) 以上の割合を求めよ。
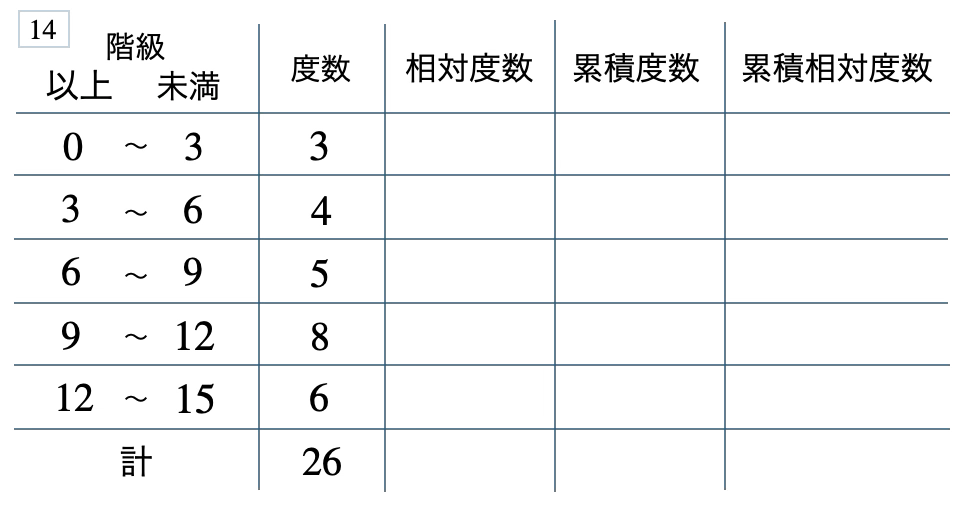
[ 解答を見る ]
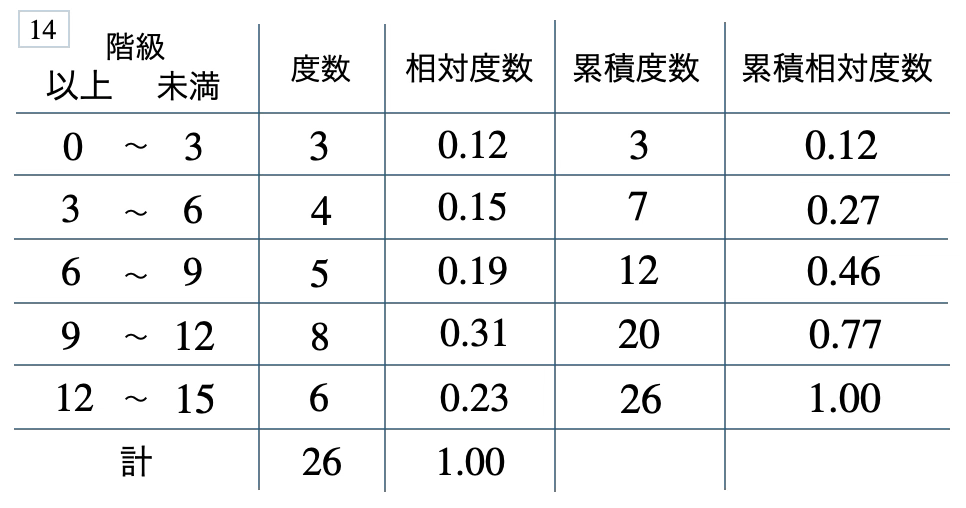
\(31\) %、\(0.54\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(9\) 未満の割合を求めよ。
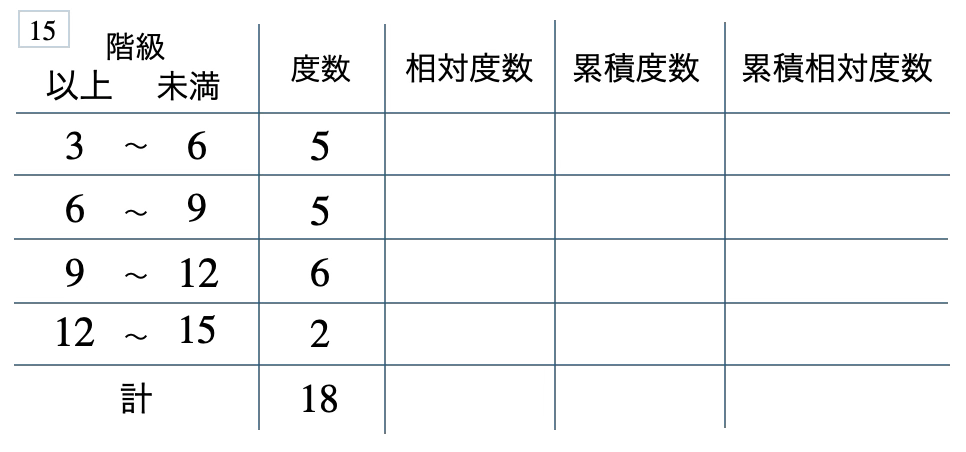
[ 解答を見る ]
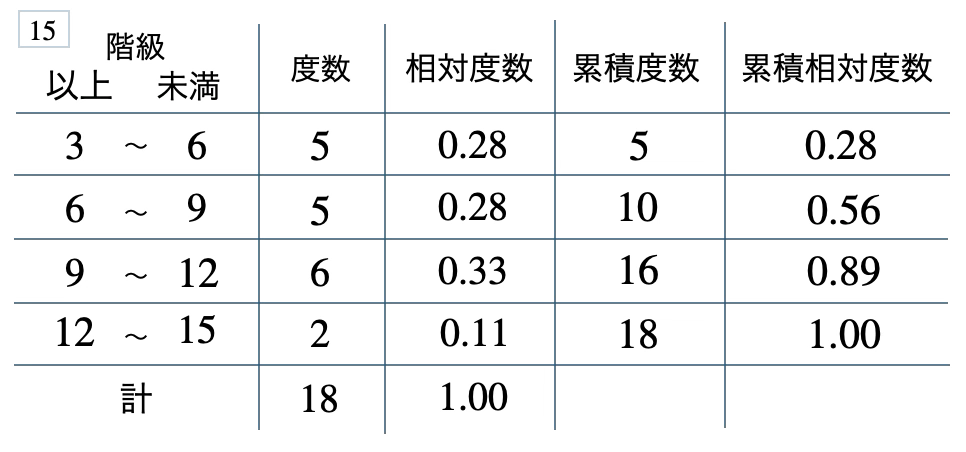
\(33\) %、\(0.56\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(12\) 以上の割合を求めよ。
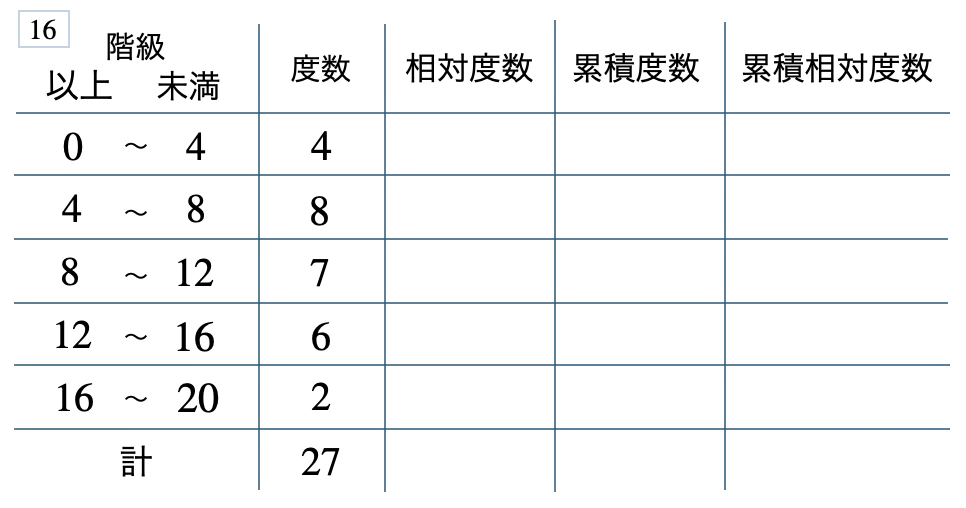
[ 解答を見る ]
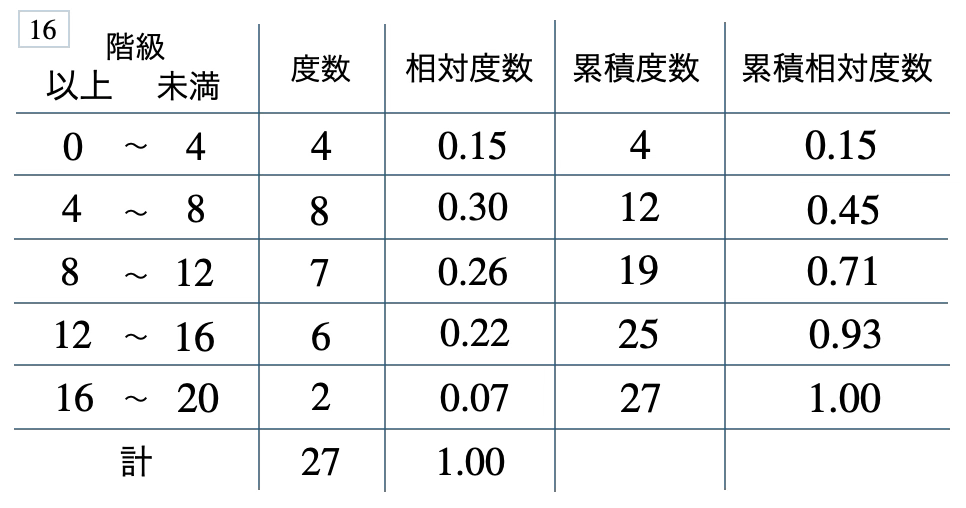
\(30\) %、\(0.29\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(8\) 未満の割合を求めよ。
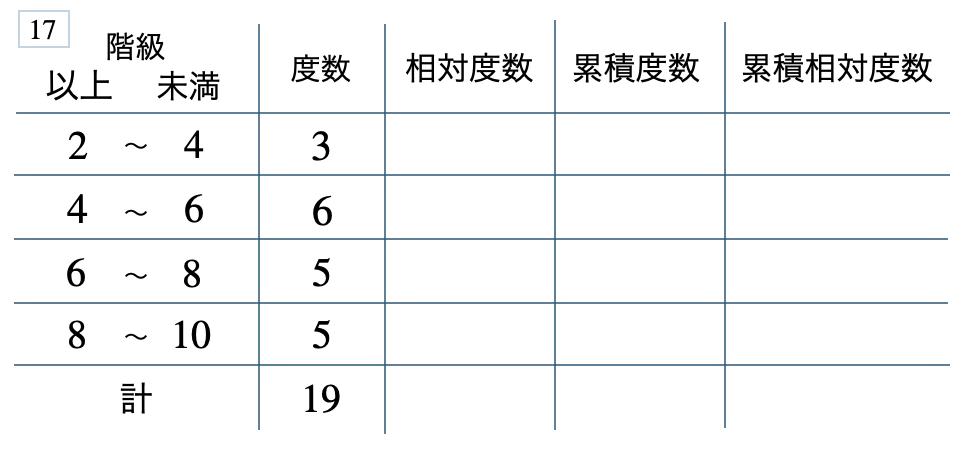
[ 解答を見る ]
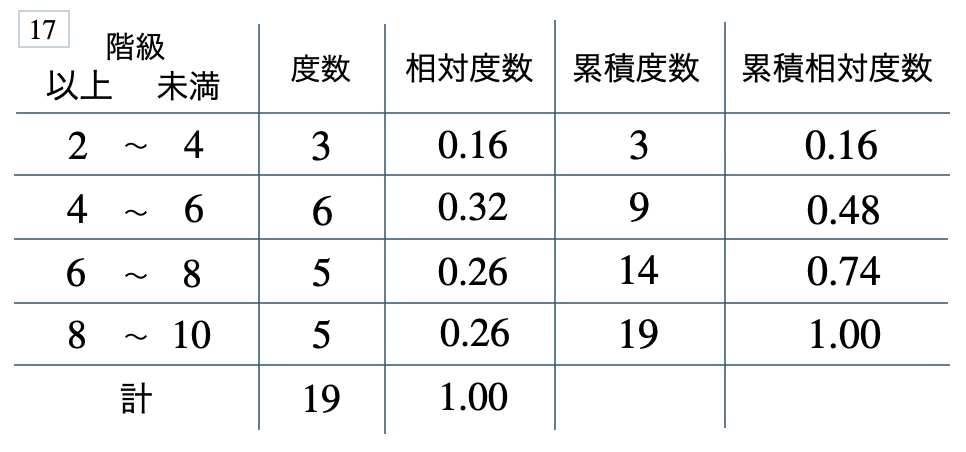
\(32\) %、\(0.74\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(10\) 以上の割合を求めよ。
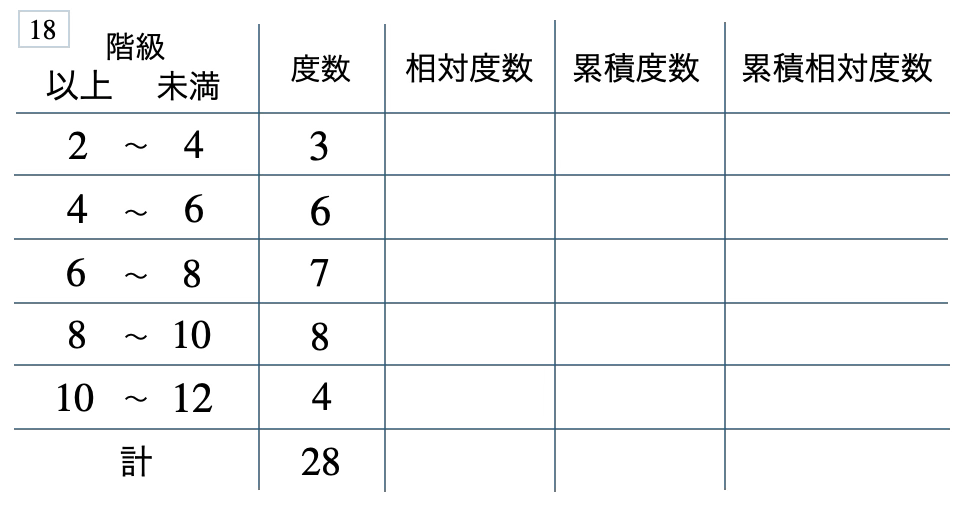
[ 解答を見る ]
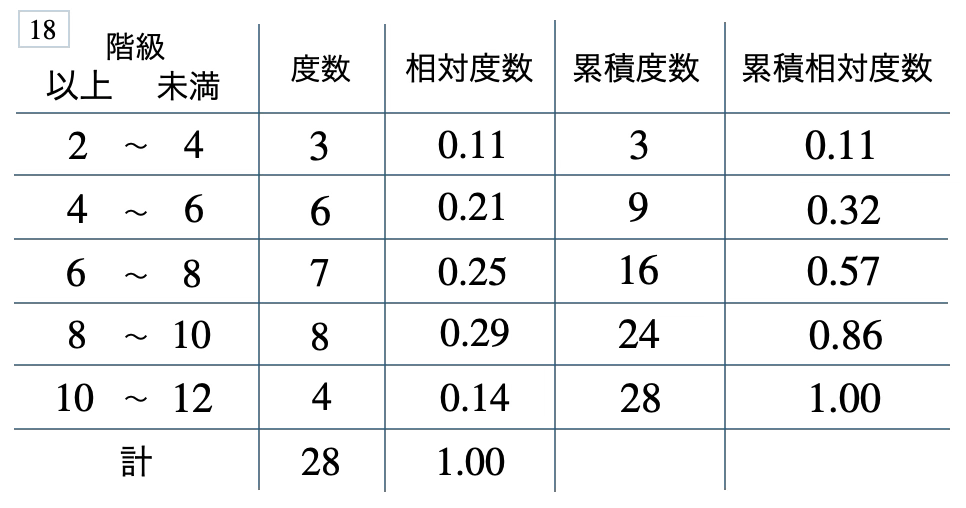
\(29\) %、\(0.14\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(7\) 未満の割合を求めよ。
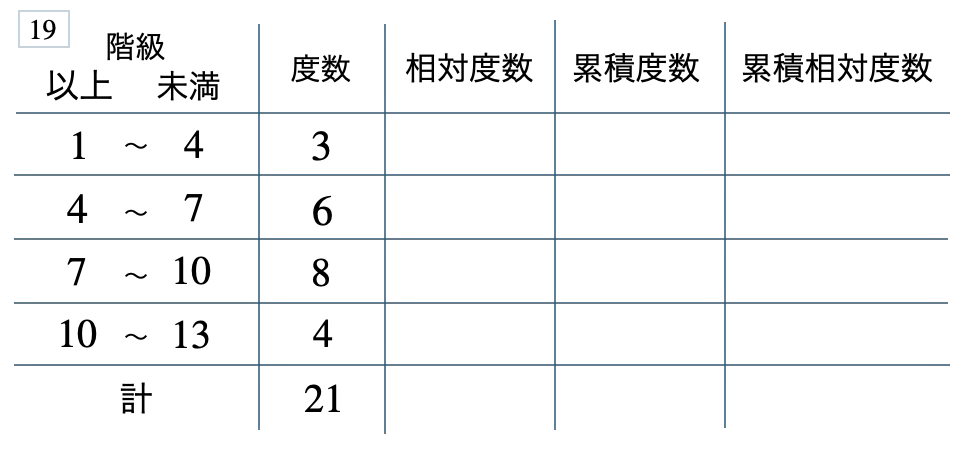
[ 解答を見る ]
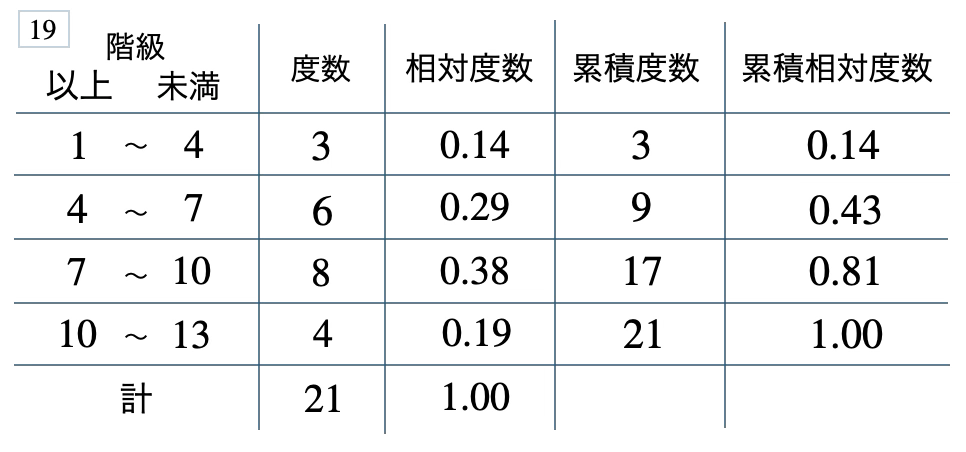
\(38\) %、\(0.43\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(7\) 以上の割合を求めよ。
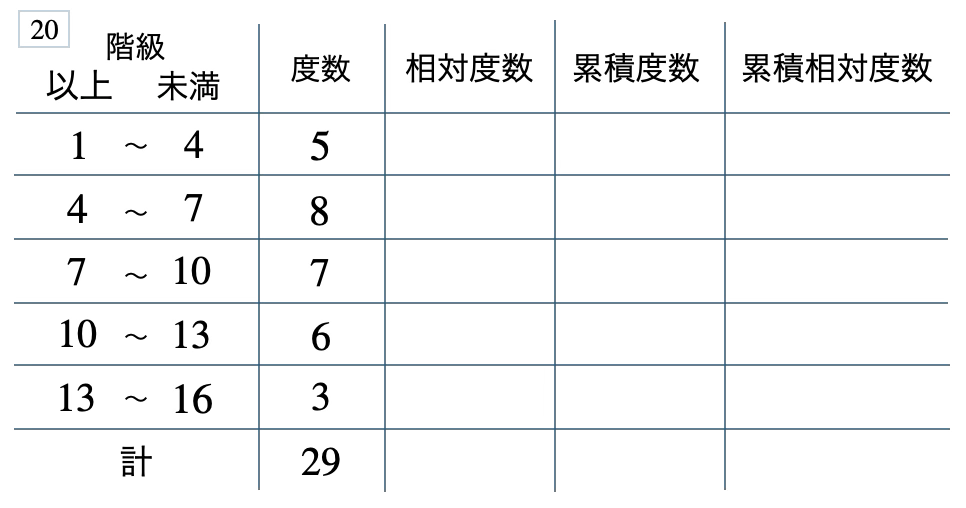
[ 解答を見る ]
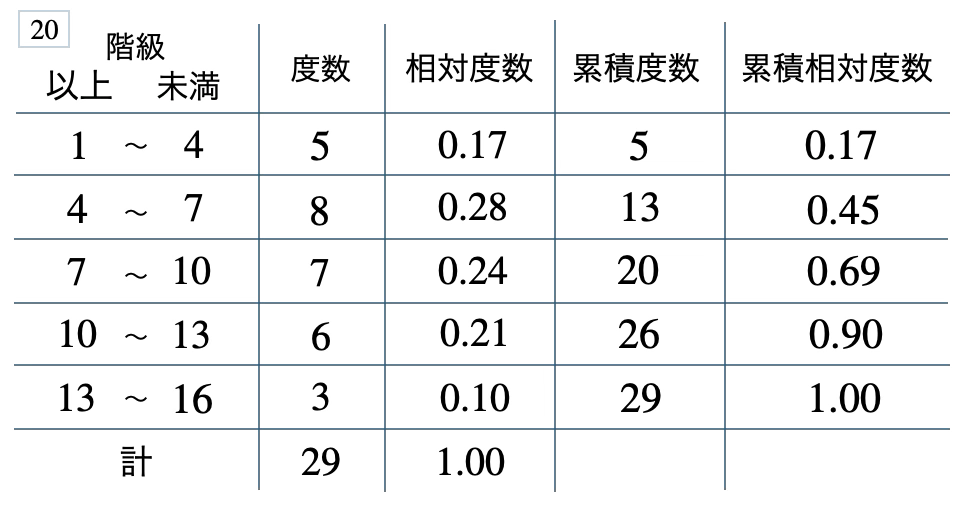
\(28\) %、\(0.55\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(6\) 未満の割合を求めよ。
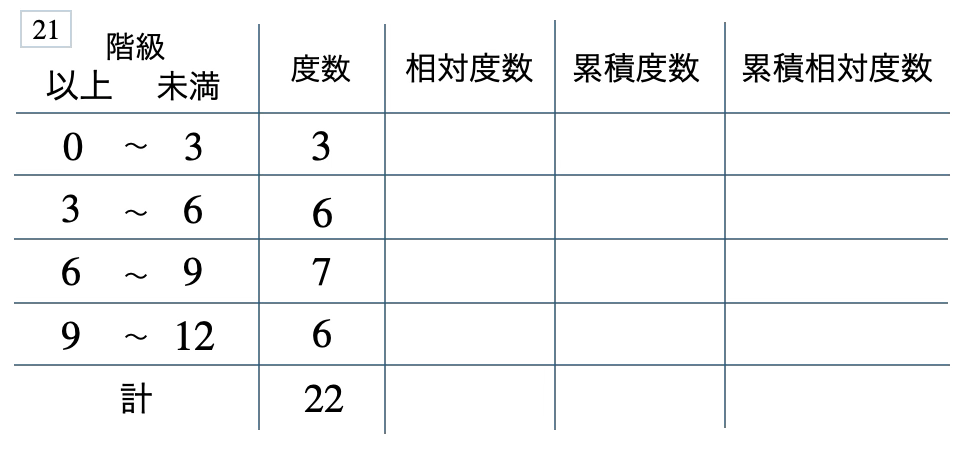
[ 解答を見る ]
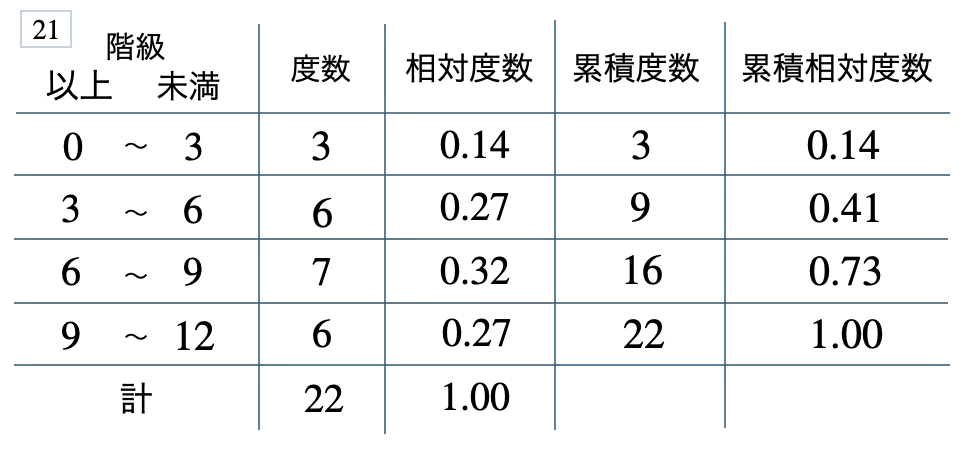
\(32\) %、\(0.41\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(12\) 以上の割合を求めよ。
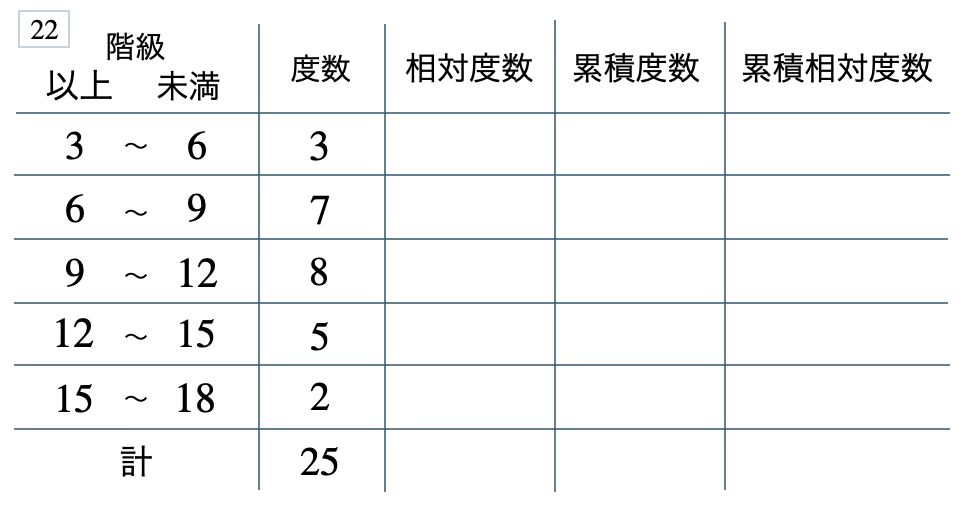
[ 解答を見る ]
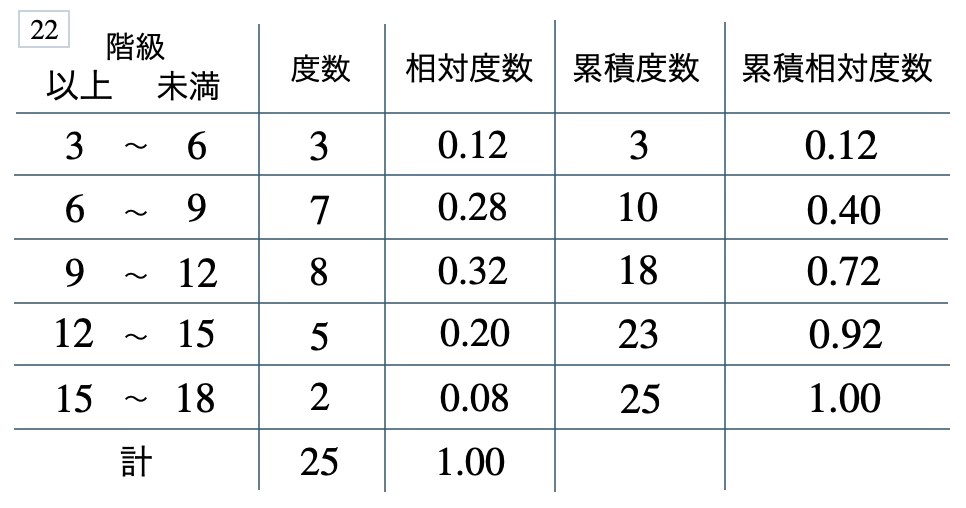
\(32\) %、\(0.28\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(8\) 未満の割合を求めよ。
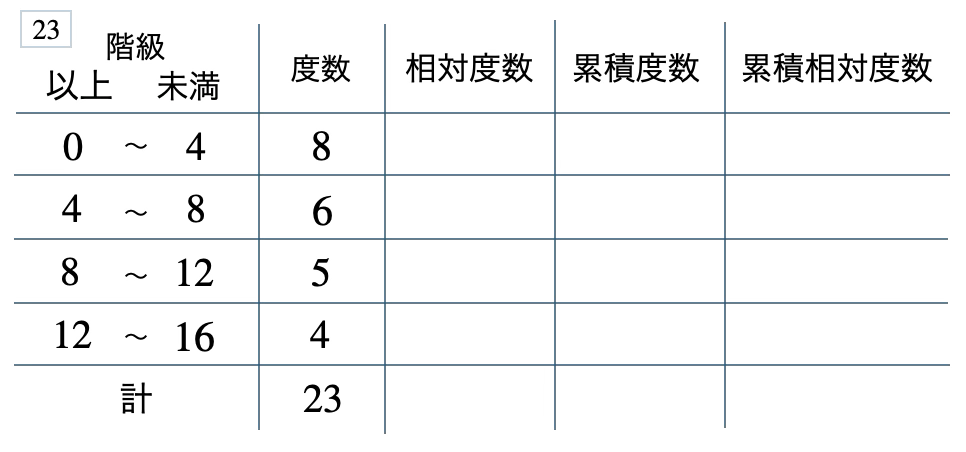
[ 解答を見る ]
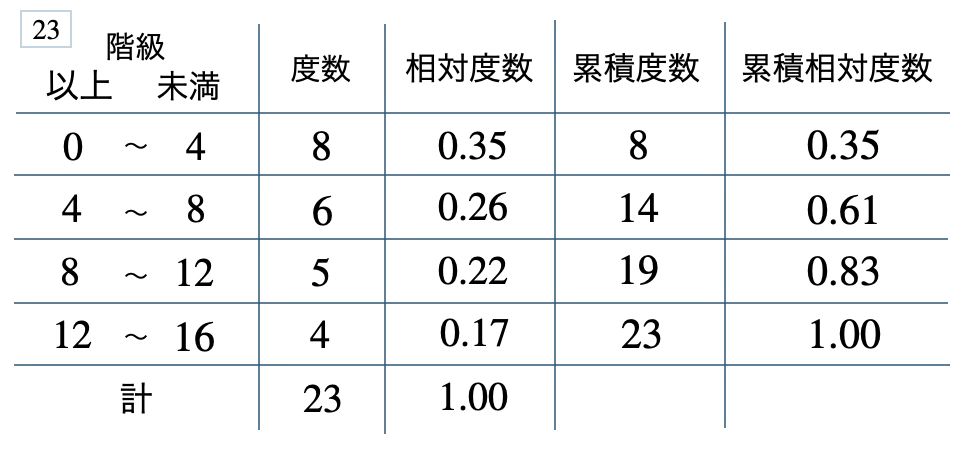
\(35\) %、\(0.61\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(9\) 以上の割合を求めよ。
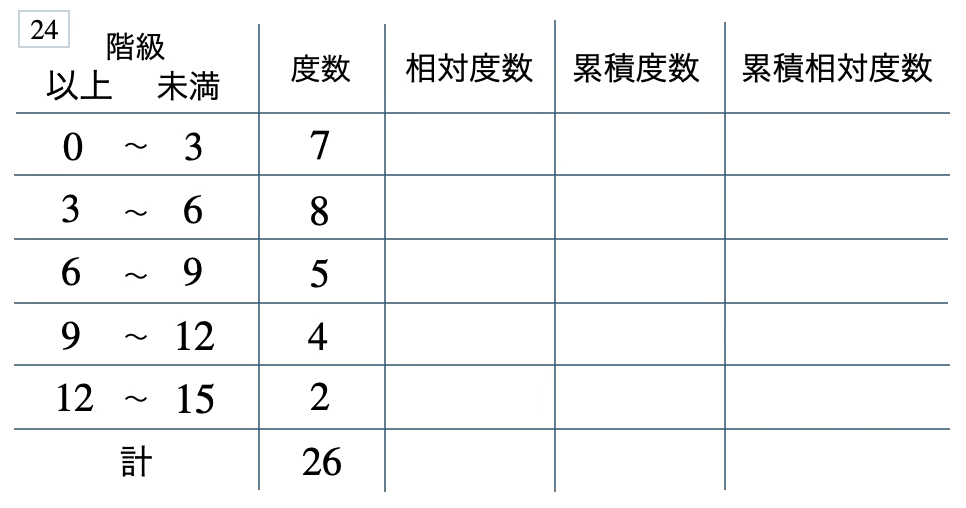
[ 解答を見る ]
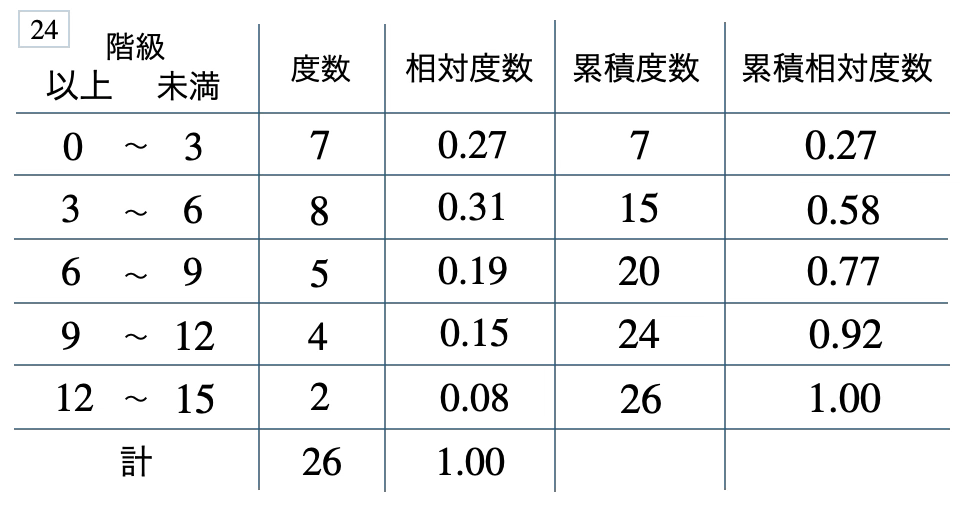
\(31\) %、\(0.23\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(12\) 以上の割合を求めよ。
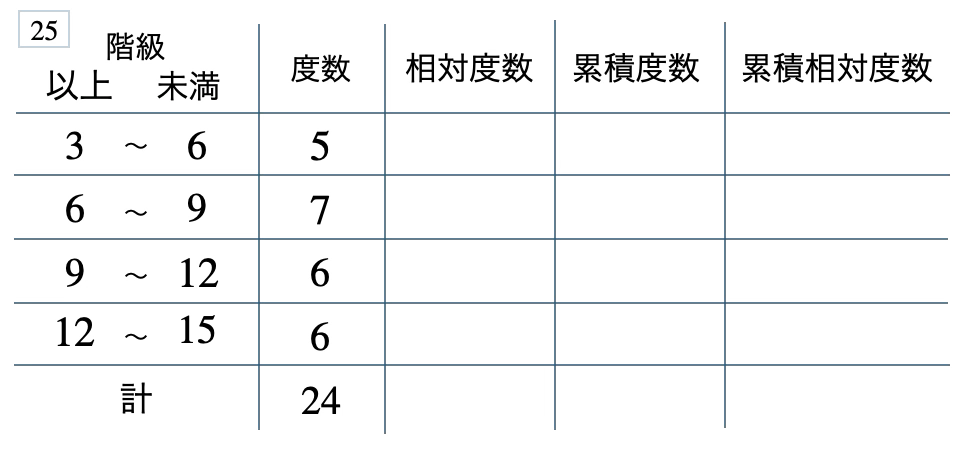
[ 解答を見る ]
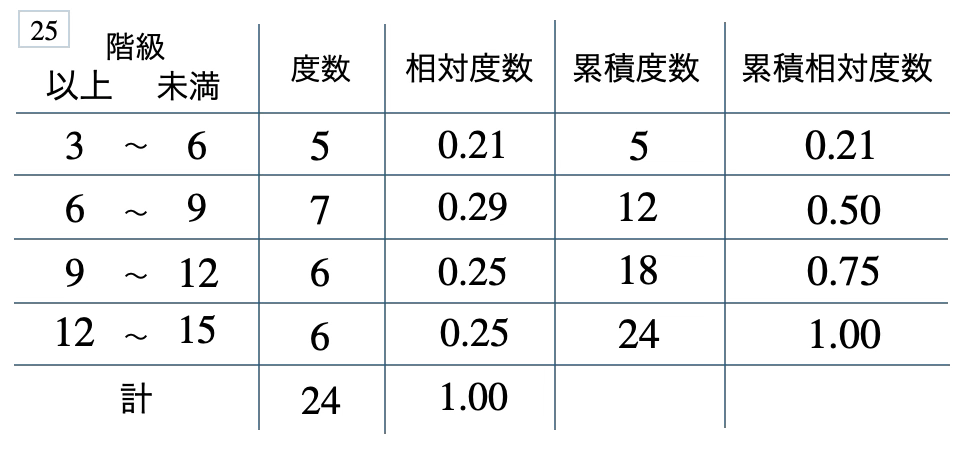
\(29\) %、\(0.25\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(12\) 以上の割合を求めよ。
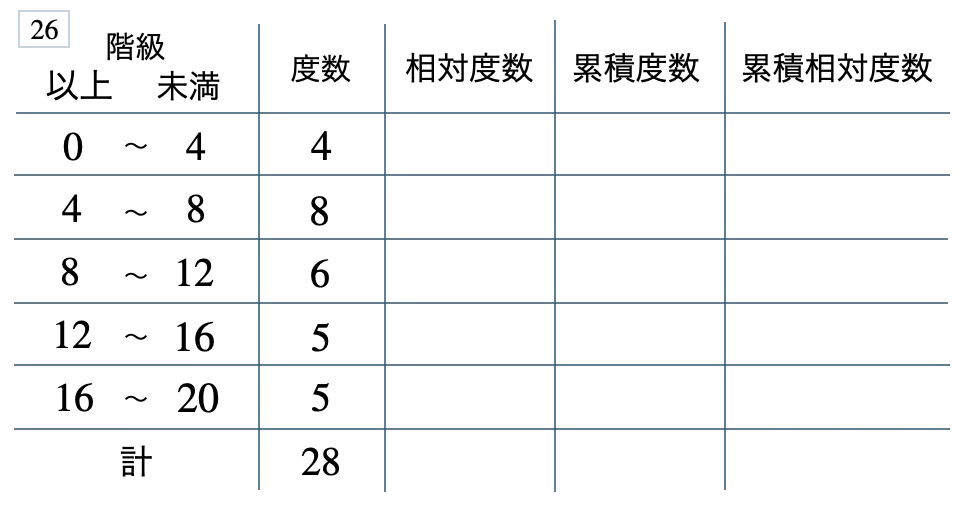
[ 解答を見る ]
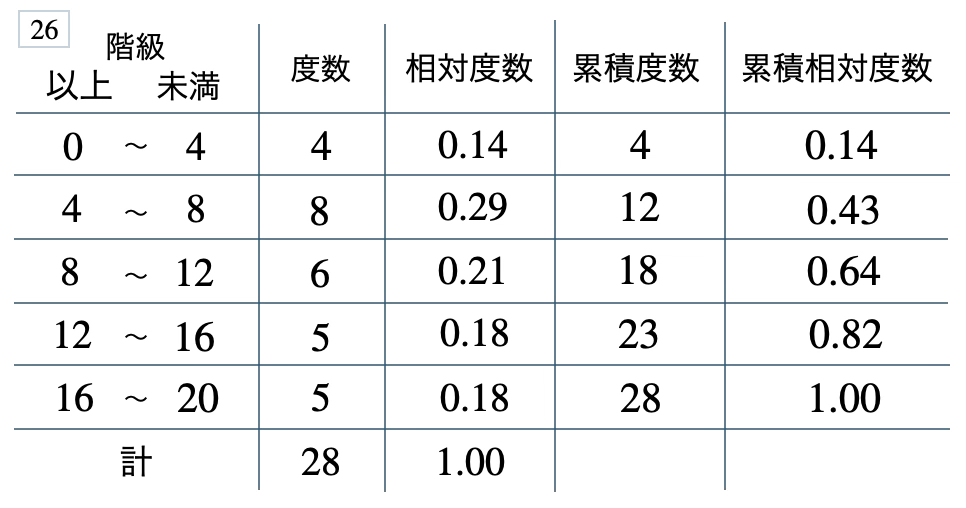
\(29\) %、\(0.36\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(6\) 未満の割合を求めよ。
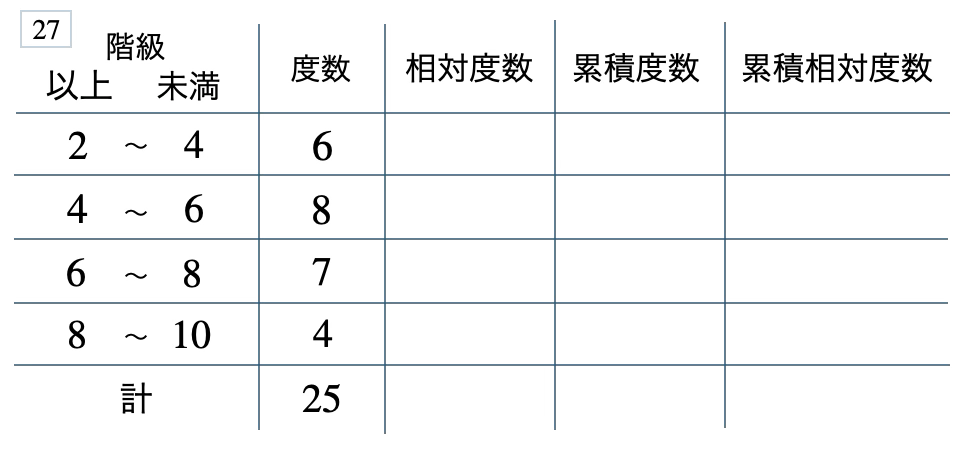
[ 解答を見る ]
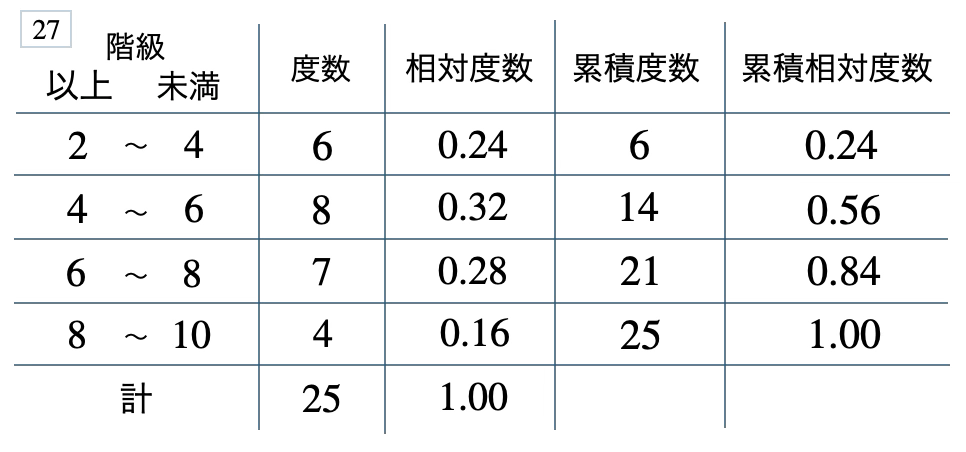
\(32\) %、\(0.56\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(10\) 以上の割合を求めよ。
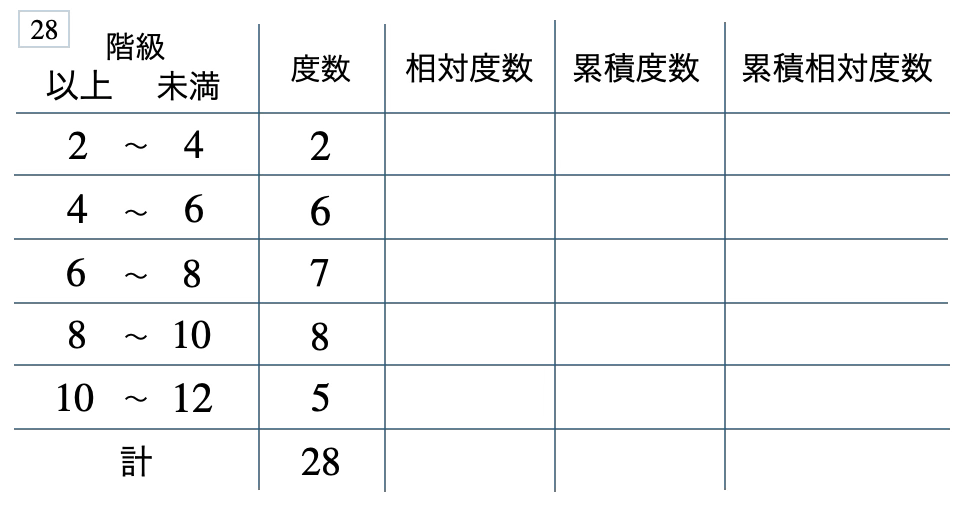
[ 解答を見る ]
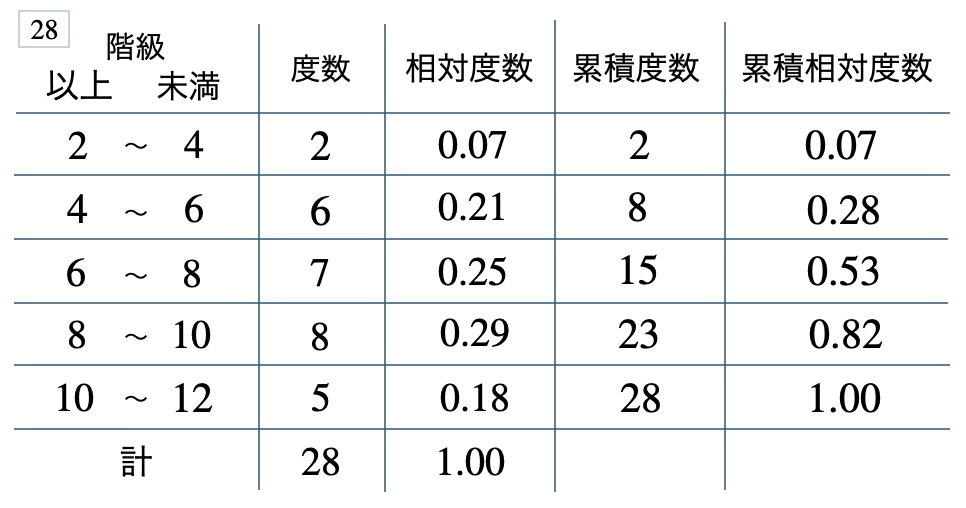
\(29\) %、\(0.18\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(10\) 以上の割合を求めよ。
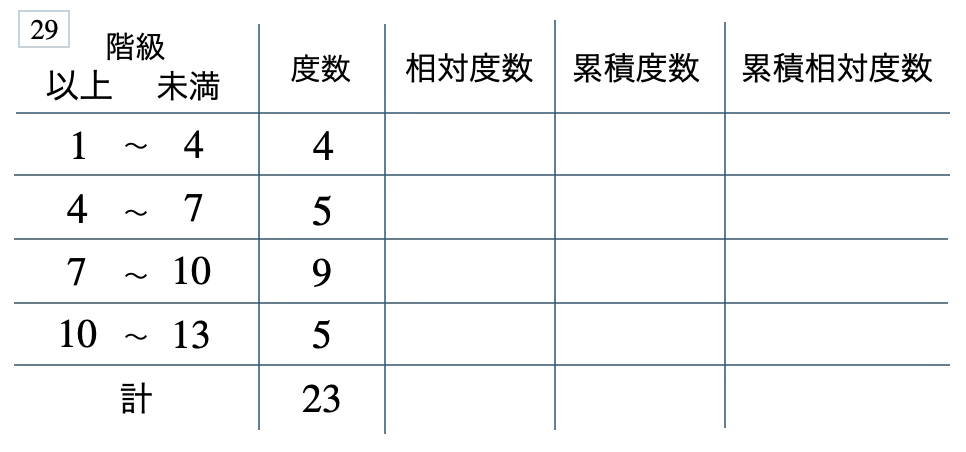
[ 解答を見る ]
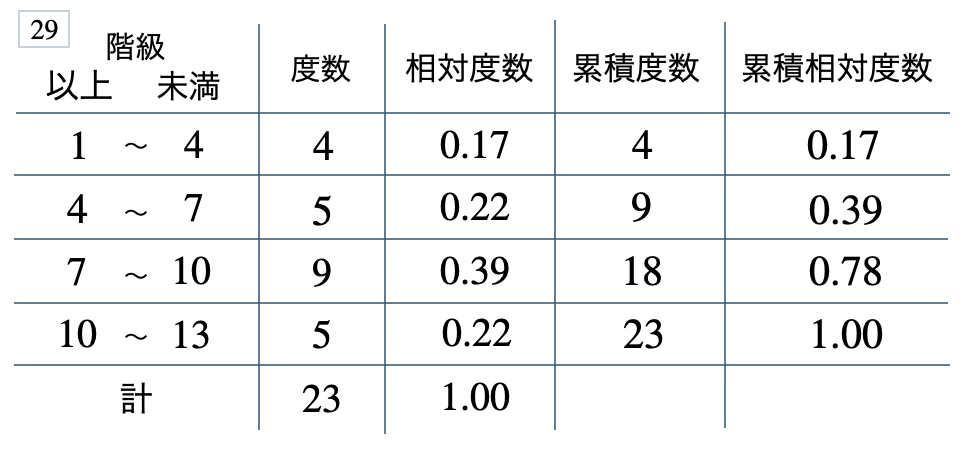
\(39\) %、\(0.22\)
次の度数分布表から相対度数、累積度数、累積相対度数の表を完成させよ。また、最頻値をとる階級は全体の何%かを求め、値が \(7\) 未満の割合を求めよ。
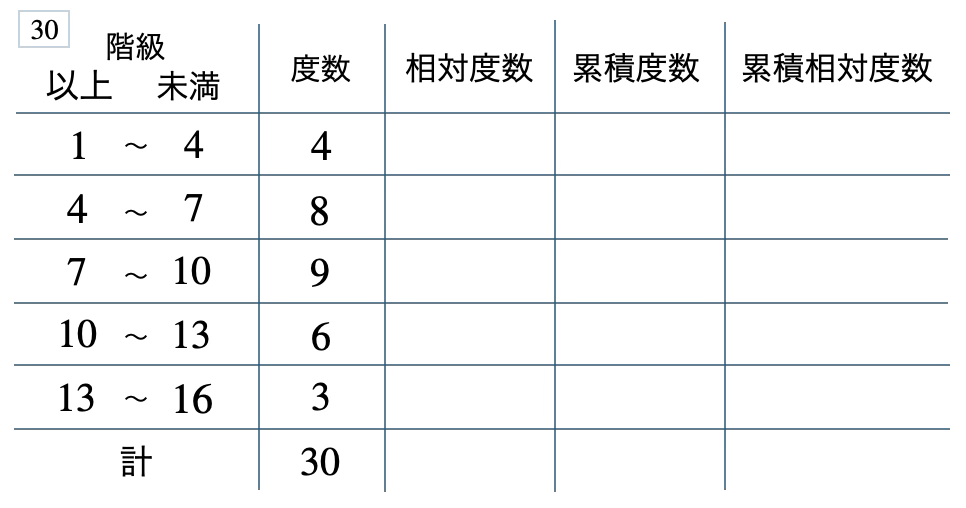
[ 解答を見る ]
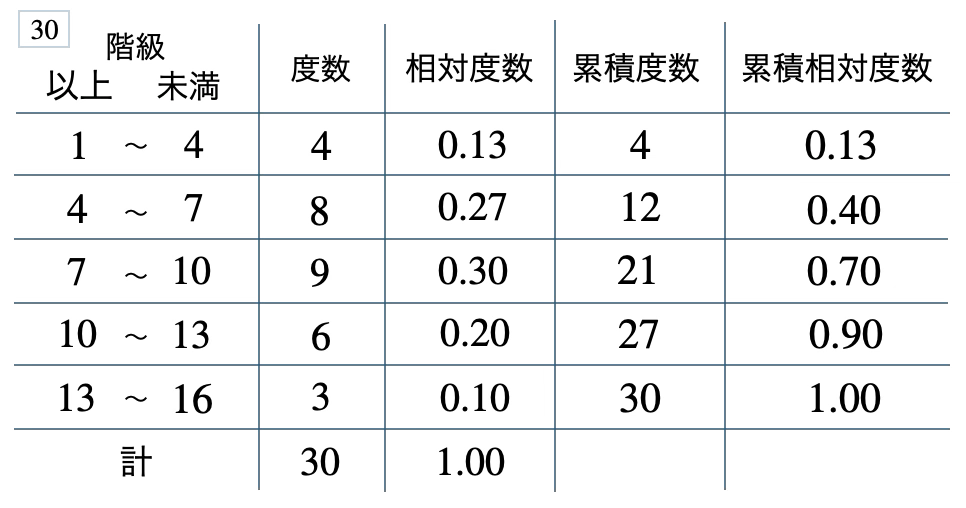
\(30\) %、\(0.40\)



