問題:平行四辺形の性質
次の問いに答えよ。
\({\small (1)}~\)平行四辺形について、次のことを答えよ。
① 平行四辺形の定義を答えよ。
② 2組の対辺についての定理を答えよ。
③ 2組の対角についての定理を答えよ。
④ 対角線についての定理を答えよ。
\({\small (2)}~\)次の図の ▱ \({\rm ABCD}\) において、次の値を求めよ。
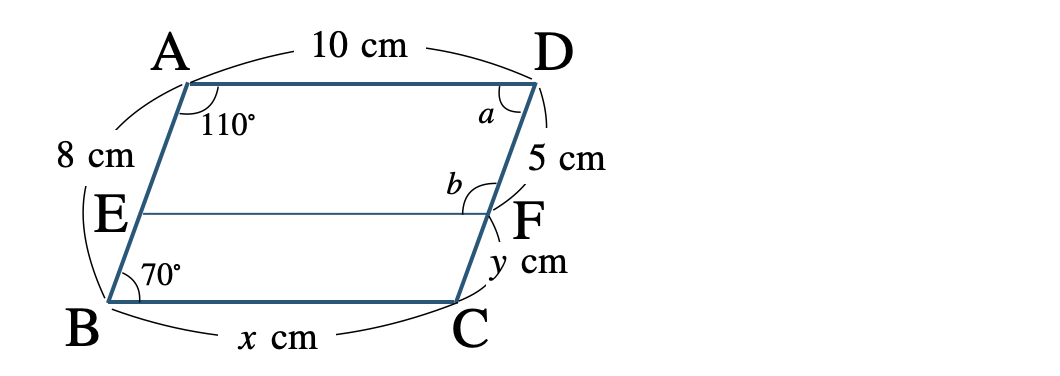
① \({\rm EF\,//\,BC}\) のとき、\(x~,~y\) の値と \(\angle a~,~\angle b\) の大きさを求めよ。
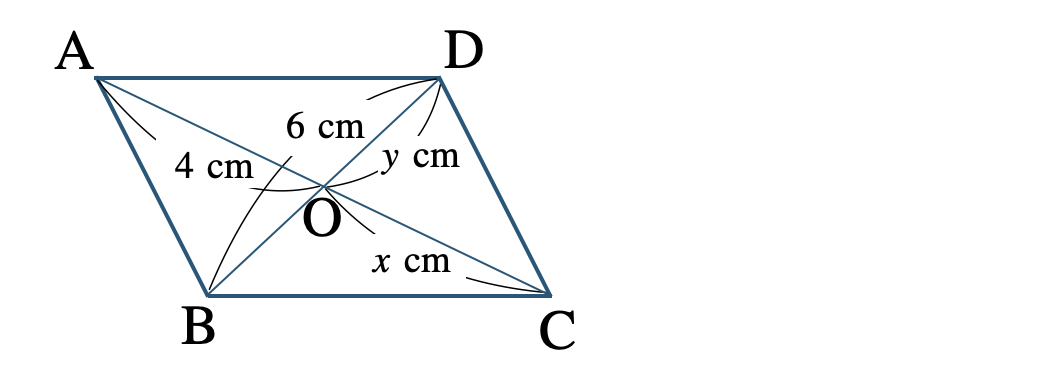
② 対角線 \({\rm AC~,~BD}\) の交点を \({\rm O}\) とするとき、\(x~,~y\) の値を求めよ。
解法のPoint
四角形の向かい合う辺を「対辺」、向かい合う角を「対角」という。
■ 平行四辺形の定義
【定義】2組の対辺がそれぞれ平行な四角形を平行四辺形という。
■ 平行四辺形の定理
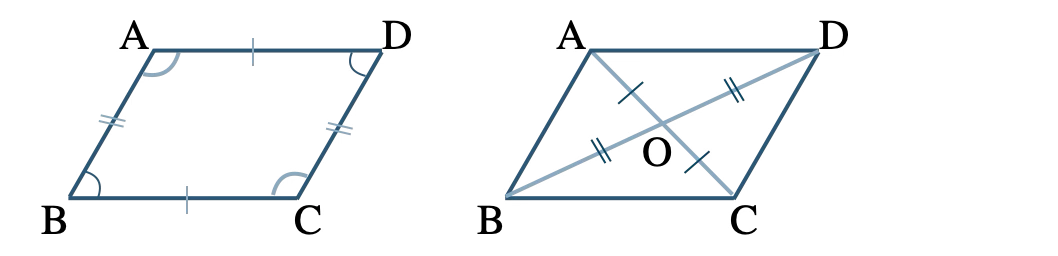
【定理】平行四辺形の対辺はそれぞれ等しい。
→ \({\rm AB=CD~,~AD=BC}\)
【定理】平行四辺形の対角はそれぞれ等しい。
→ \(\angle{\rm A}=\angle{\rm C}~,~\angle{\rm B}=\angle{\rm D}\)
【定理】平行四辺形の対角線はそれぞれの中点で交わる。
→ \({\rm AO=CO~,~BO=DO}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:平行四辺形の性質
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)平行四辺形について、次のことを答えよ。
① 平行四辺形の定義を答えよ。
② 2組の対辺についての定理を答えよ。
③ 2組の対角についての定理を答えよ。
④ 対角線についての定理を答えよ。
① 平行四辺形の定義より、
2組の対辺がそれぞれ平行な四角形を平行四辺形という
② 2組の対辺についての定理より、
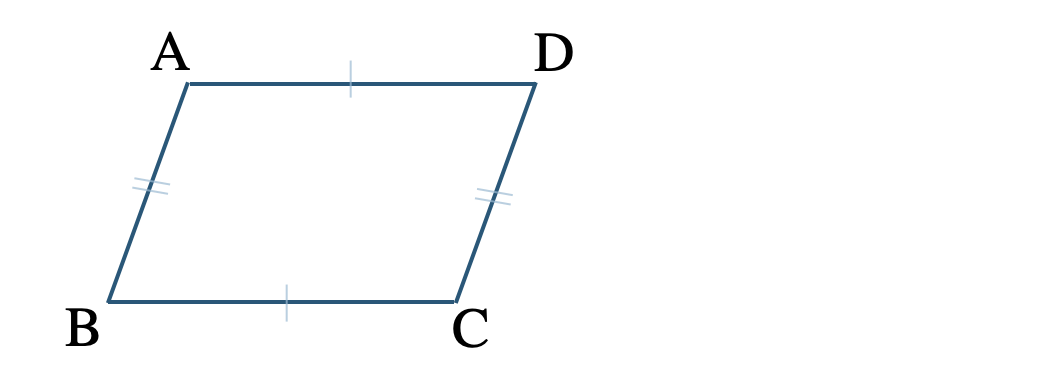
平行四辺形の対辺はそれぞれ等しい
③ 2組の対角についての定理より、
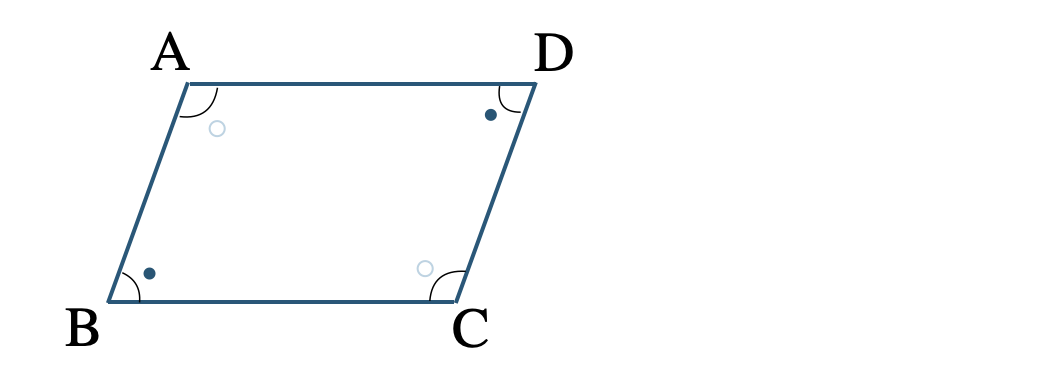
平行四辺形の対角はそれぞれ等しい
④ 対角線についての定理より、
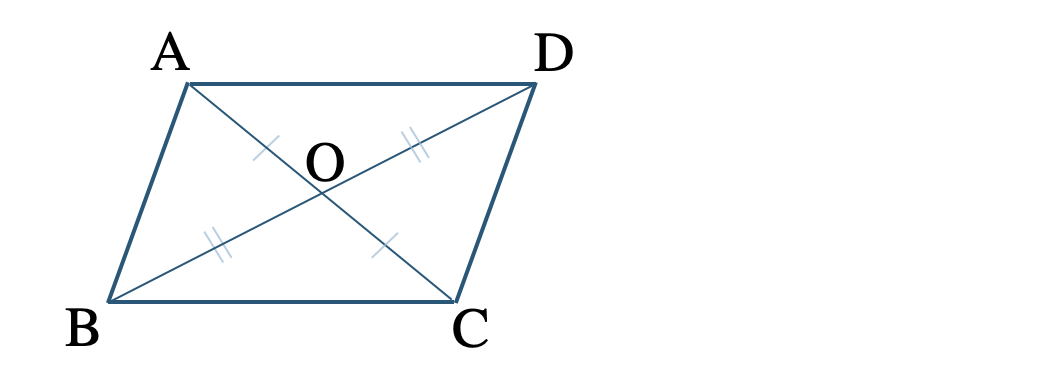
平行四辺形の対角線はそれぞれの中点で交わる
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の図の ▱ \({\rm ABCD}\) において、次の値を求めよ。
① \({\rm EF\,//\,BC}\) のとき、\(x~,~y\) の値と \(\angle a~,~\angle b\) の大きさを求めよ。

② 対角線 \({\rm AC~,~BD}\) の交点を \({\rm O}\) とするとき、\(x~,~y\) の値を求めよ。

① 平行四辺形の対辺は等しいので、
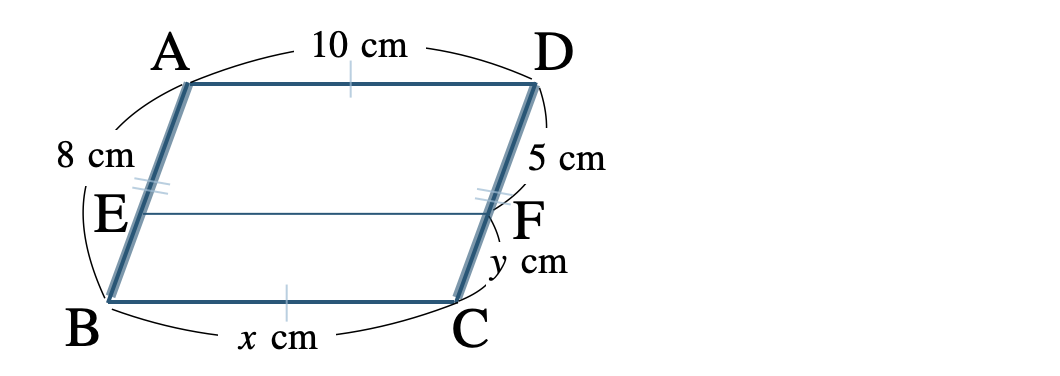
\({\rm AD=BC}\) より、\(x=10~{\rm cm}\)
また、\({\rm AB=DC}\) より、
\(\begin{eqnarray}~~~8&=&5+y\\[2pt]~~~5+y&=&8\\[2pt]~~~y&=&8-5\\[2pt]~~~y&=&3~{\rm cm}\end{eqnarray}\)
次に、平行四辺形の対角は等しいので、
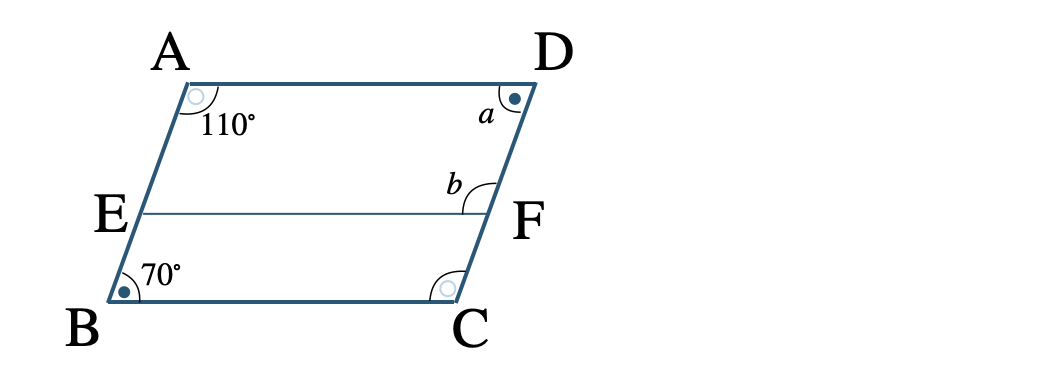
\(\angle{\rm B}=\angle{\rm D}\) より、\(a=70^\circ\)
また、\(\angle{\rm A}=\angle{\rm C}\) より、\(\angle{\rm C}=110^\circ\)
\({\rm EF\,//\,BC}\) より、同位角が等しいので、
\(\angle{\rm DFE}=\angle{\rm C}\) となり、
\(\begin{split}~~~b=110^\circ\end{split}\)
したがって、
\(\begin{split}~~~x=10~{\rm cm}~,~y=3~{\rm cm}~,~a=70^\circ~,~b=110^\circ\end{split}\)
となる
② 平行四辺形の対角線はそれぞれの中点で交わるので、
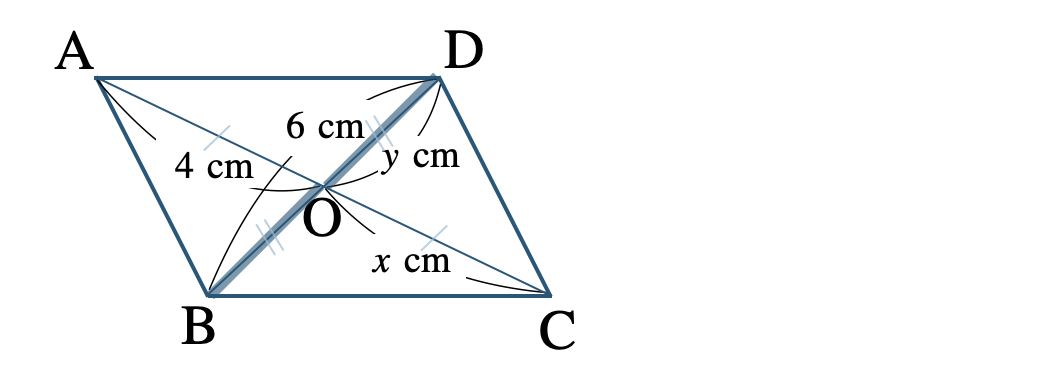
\({\rm AO=CO}\) より、\(x=4~{\rm cm}\)
また、\({\rm BO=DO}\) より \(\begin{split}{\rm DO={ \frac{\,1\,}{\,2\,}}BD}\end{split}\) となるので、
\(\begin{split}~~~y=\frac{\,1\,}{\,2\,}\times6=3~{\rm cm}\end{split}\)
したがって、
\(\begin{split}~~~x=4~{\rm cm}~,~y=3~{\rm cm}\end{split}\)
となる



