数え方の樹形図

Point：数え方の樹形図

■ 選ぶだけのパターン

---

Ａ、Ｂ、Ｃの \(3\) 文字から \(2\) 文字を選ぶときは、

これら \(3\) 通りとなる

---

※ Ｂ-ＡなどはＡ-Ｂと同じになるのでかかない

---

■ 選んで並べるパターン

---

Ａ、Ｂ、Ｃの \(3\) 文字から \(2\) 文字を選んで並べるときは、

これら \(6\) 通りとなる

---

※ Ａ-ＢとＢ-Ａは並べ方が違うので別の場合の数となる

---

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

問題

次の問いに答えよ。

---

\({\small (1)}~\)\(5\) 人の生徒の中から \(2\) 人の委員を選ぶとき、選び方は全部で何通りあるか答えよ。

\(5\) 人をＡ、Ｂ、Ｃ、Ｄ、Ｅと区別すると、この中から \(2\) 人の委員を選ぶので、
選ぶだけのパターンとなる

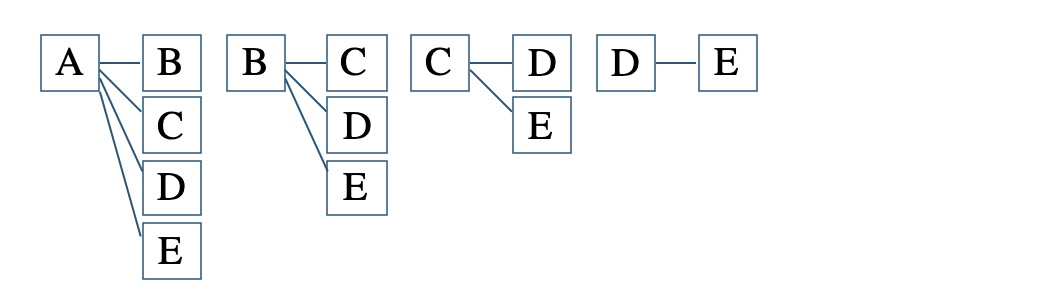
※ Ｂ-ＡなどはＡ-Ｂと同じになるのでかかない

---

これより、

---

\(\begin{split}~~~4+3+2+1=10\end{split}\)

---

したがって、答えは、\(10\) 通りとなる

問題

次の問いに答えよ。

---

\({\small (2)}~\)\(5\) 人の生徒の中から委員長と副委員長を選ぶとき、選び方は全部で何通りあるか答えよ。

\(5\) 人をＡ、Ｂ、Ｃ、Ｄ、Ｅと区別すると、委員長と副委員長を選ぶので、
選んで並べるパターンとなる

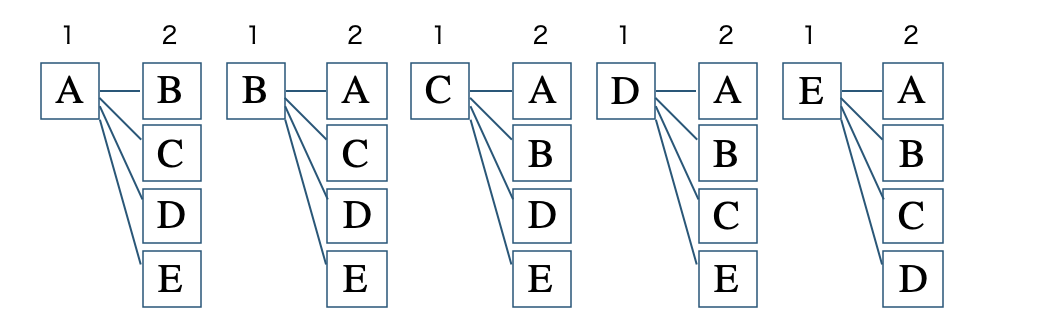
※ Ａ-ＢとＢ-Ａは並べ方が違うので別の場合の数となる

---

これより、

---

\(\begin{split}~~~4\times5=20\end{split}\)

---

したがって、答えは、\(20\) 通りとなる

問題

次の問いに答えよ。

---

\({\small (3)}~\)\(5\) 人の生徒の中から \(3\) 人の委員を選ぶとき、選び方は全部で何通りあるか答えよ。

\(5\) 人をＡ、Ｂ、Ｃ、Ｄ、Ｅと区別すると、この中から \(3\) 人の委員を選ぶので、
選ぶだけのパターンとなる

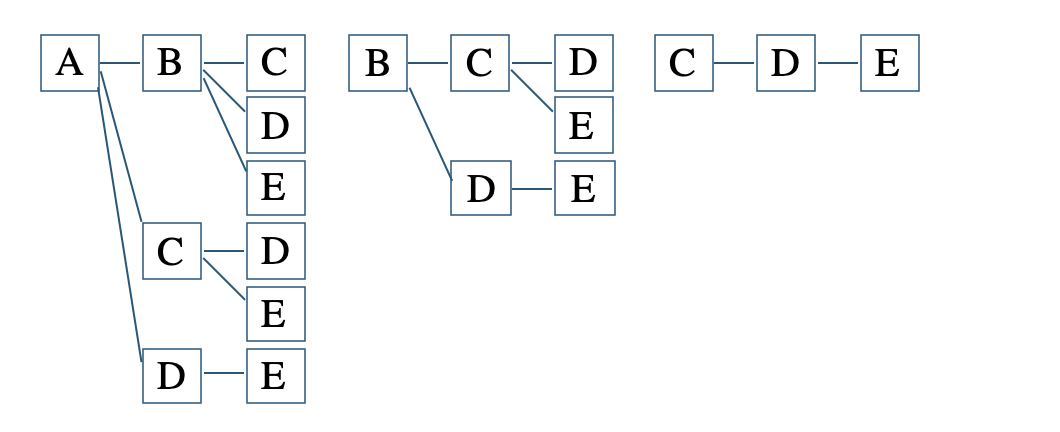
これより、

---

\(\begin{split}~~~6+3+1=10\end{split}\)

---

したがって、答えは、\(10\) 通りとなる

問題

次の問いに答えよ。

---

\({\small (4)}~\)\(3\) 人の選手のリレーの順番を決めるとき、選び方は全部で何通りあるか答えよ。

\(3\) 人をＡ、Ｂ、Ｃと区別すると、１番目、２番目、３番目を選ぶので、
選んで並べるパターンとなる

これより、

---

\(\begin{split}~~~2\times3=6\end{split}\)

---

したがって、答えは、\(6\) 通りとなる

問題

次の問いに答えよ。

---

\({\small (5)}~\)\(6\) 人で一対一の対戦ゲームをする。それぞれ１回ずつ対戦するとき、全部で何試合することになるか答えよ。

\(6\) 人をＡ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆと区別すると、この中から対戦する \(2\) 人を選ぶので、
選ぶだけのパターンとなる

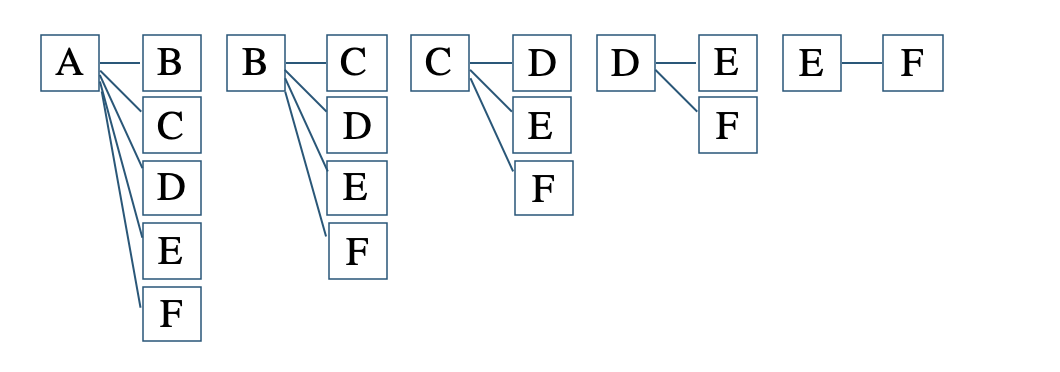
これより、

---

\(\begin{split}~~~5+4+3+2+1=15\end{split}\)

---

したがって、答えは、\(15\) 試合となる