さいころを投げる確率

Point：さいころを投げる確率

２個のさいころを投げる確率の求め方は、

---

① ２個のさいころをＡ、Ｂと区別をして、出た目の表を作る。

　この表で、
　\(({\rm A~,~B})=(1~,~2)\) と \(({\rm A~,~B})=(2~,~1)\)
　は別の場合の数となる。

---

　よって、起こりうる場合の数は全部で、
　\(6\times6=36\) 通りとなり、同様に確からしい。

---

② 条件に合う場合の数を表より数えて、確率を求める。

---

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

問題

２個のさいころを同時に投げるとき、次の確率を求めよ。

---

\({\small (1)}~\)同じ目が出る確率

２個のさいころをＡ、Ｂと区別をして、出た目の表を作ると、

これより、起こりうる場合の数は全部で、
\(6\times6=36\) 通りとなる

---

また、同じ目となる場合は、

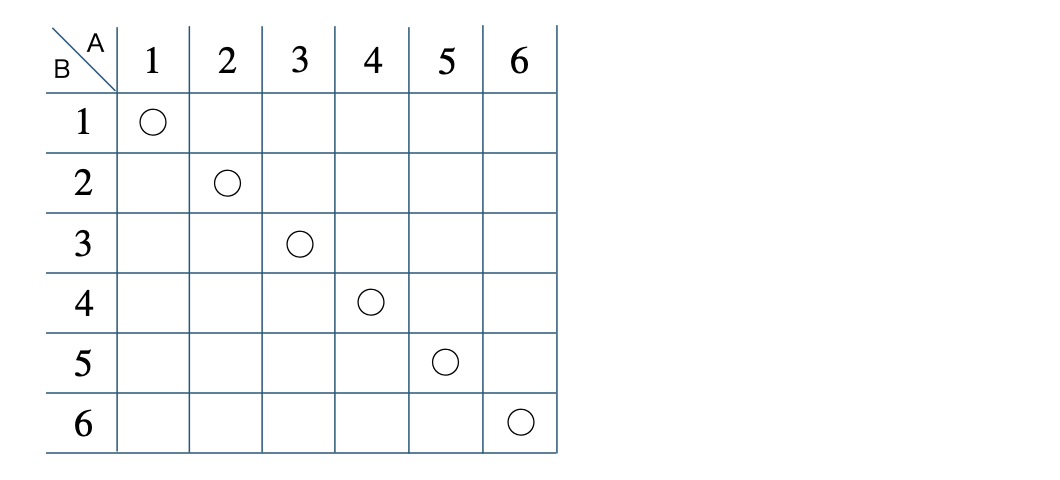
◯を付けた \(6\) 通りとなるので、

---

\(\begin{split}~~~\frac{\,6\,}{\,36\,}=\frac{\,1\,}{\,6\,}\end{split}\)

---

したがって、答えは \(\begin{split}{ \frac{\,1\,}{\,6\,}}\end{split}\) となる

問題

２個のさいころを同時に投げるとき、次の確率を求めよ。

---

\({\small (2)}~\)出る目の和が \(6\) となる確率

\({\small (1)}\) の表より、出る目の和が \(6\) となる場合は、

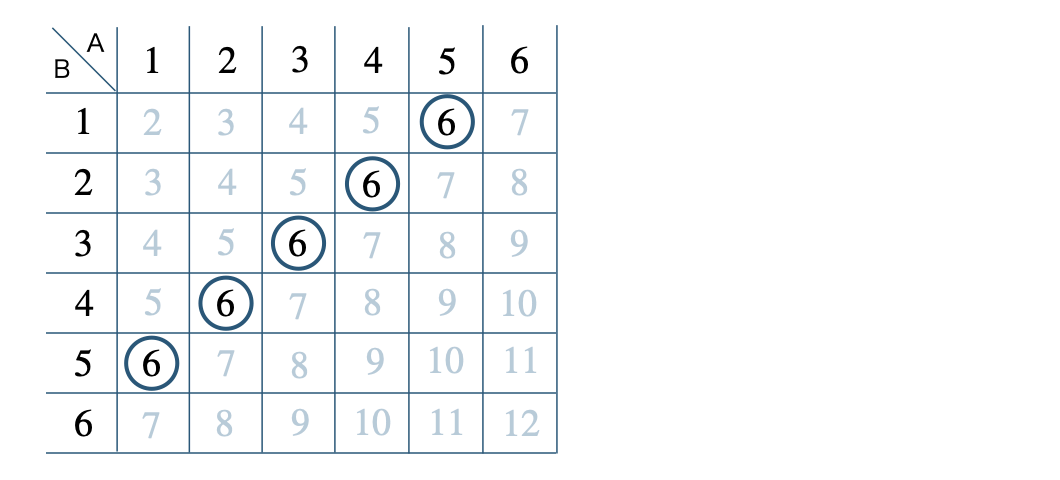
◯を付けた \(5\) 通りとなるので、

---

したがって、答えは \(\begin{split}{\frac{\,5\,}{\,36\,}}\end{split}\) となる

問題

２個のさいころを同時に投げるとき、次の確率を求めよ。

---

\({\small (3)}~\)出る目の積が奇数となる確率

\({\small (1)}\) の表より、出る目の積が奇数となる場合は、

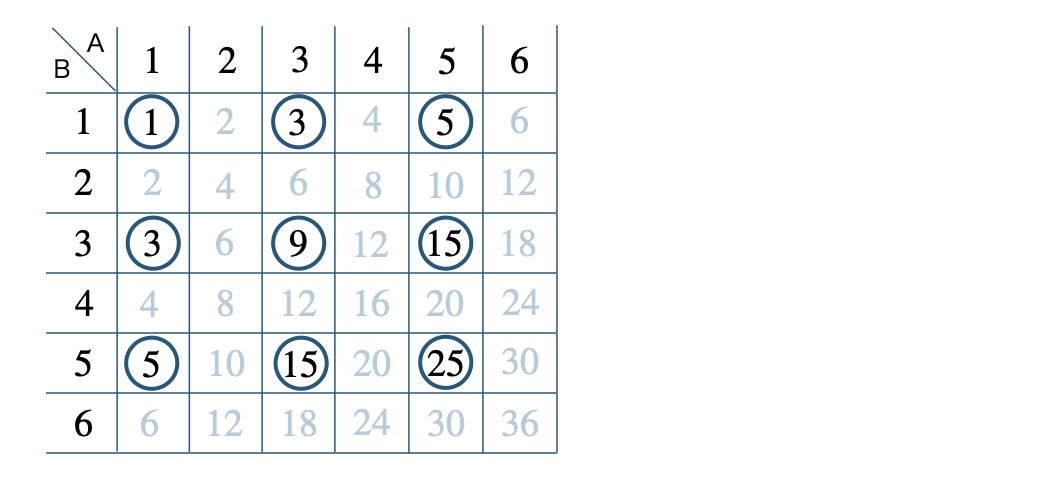
◯を付けた \(9\) 通りとなるので、

---

\(\begin{split}~~~\frac{\,9\,}{\,36\,}=\frac{\,1\,}{\,4\,}\end{split}\)

---

したがって、答えは \(\begin{split}{\frac{\,1\,}{\,4\,}}\end{split}\) となる

問題

２個のさいころを同時に投げるとき、次の確率を求めよ。

---

\({\small (4)}~\)違う目が出る確率

違う目が出る確率は、
　１ー(同じ目が出る確率) となるので、
\({\small (1)}\) の答えより、同じ目が出る確率は \(\begin{split}{\frac{\,1\,}{\,6\,}}\end{split}\) であるので、

---

\(\begin{split}~~~1-\frac{\,1\,}{\,6\,}=\frac{\,6-1\,}{\,6\,}=\frac{\,5\,}{\,6\,}\end{split}\)

---

したがって、答えは \(\begin{split}{\frac{\,5\,}{\,6\,}}\end{split}\) となる