このページは「中学数学2 合同な図形」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう!
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
【問題一覧】中学数学2 合同な図形
平行線と角
次の問いに答えよ。
\({\small (1)}~\)次の角を記号で答えよ。
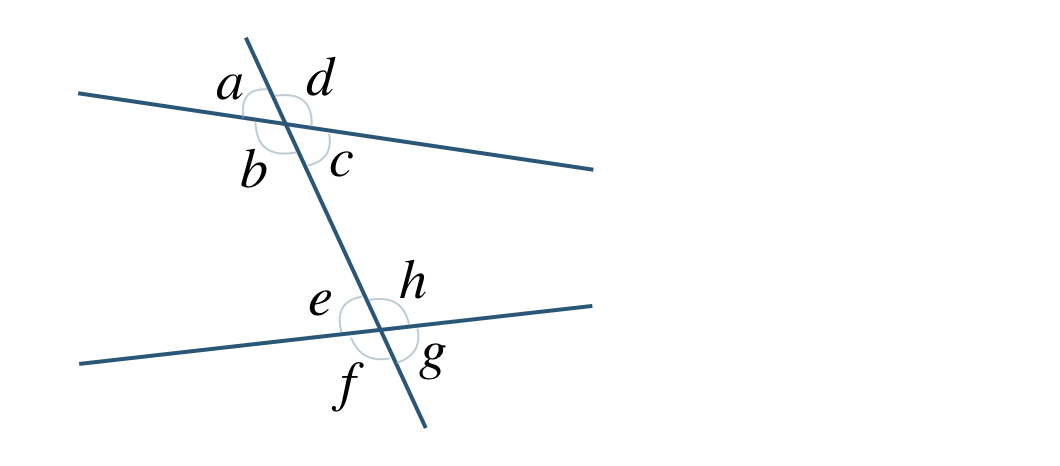
① \(\angle a\) の対頂角。
② \(\angle a\) の同位角。
③ \(\angle b\) の錯角。
④ \(\angle c\) の錯角。
\({\small (2)}~\)次の図において、
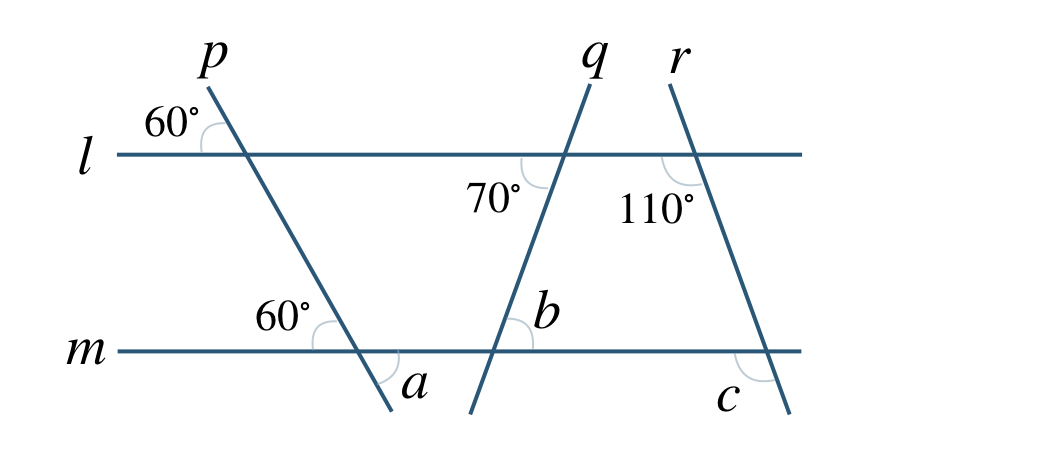
① \(l\,//\,m\) であることを説明せよ。
② \(\angle a~,~\angle b~,~\angle c\) の大きさを求めよ。
\({\small (3)}~\)次の図で \(l\,//\,m\) のとき、\(\angle x\) の大きさを求めよ。
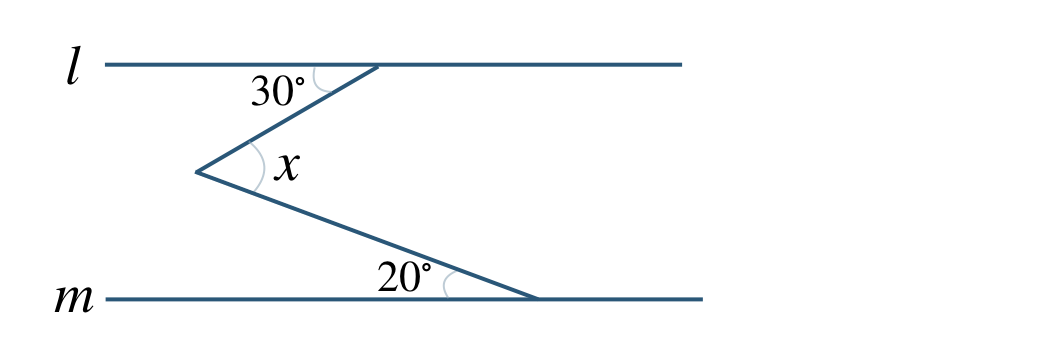
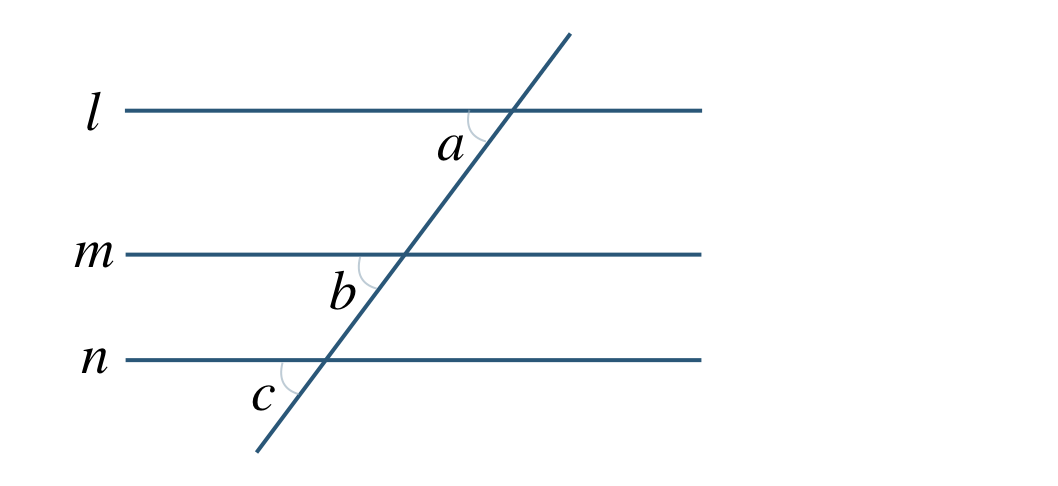
\({\small (4)}~\)次の図で、
\(l\,//\,m~,~l\,//\, n\) ならば \(m\,//\,n\)
を説明せよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(\angle c\) ② \(\angle e\)
③ \(\angle h\) ④ \(\angle e\)
\({\small (2)}~\)
① 直線 \(p\) に対する同位角が \(60^\circ\) で等しいので、2直線が平行 \(l\,//\,m\) となる
② \(\angle a=60^\circ~,~\angle b=70^\circ~,~\angle c=110^\circ\)
\({\small (3)}~\)\(\angle x=50^\circ\)
\({\small (4)}~\)\(l\,//\,m\) の同位角が等しいことより、
\(~~~\angle a=\angle b\)
\(l\,//\,n\) の同位角が等しいことより、
\(~~~\angle a=\angle c\)
よって、
\(~~~\angle b=\angle c\)
同位角が等しいので、2直線 \(m~,~n\) が平行となり、\(m\,//\,n\)

三角形の内角と外角
次の問いに答えよ。
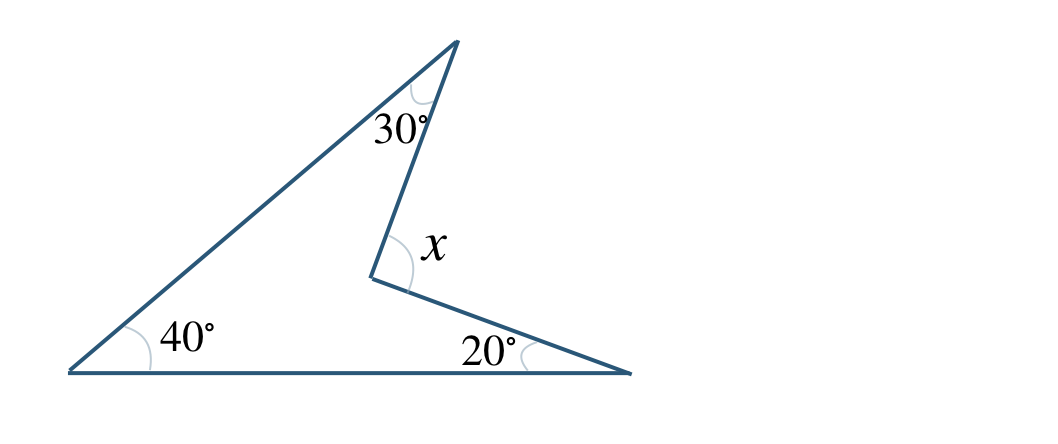
\({\small (1)}~\)次の図において、\(\angle x\) の大きさを求めよ。
①
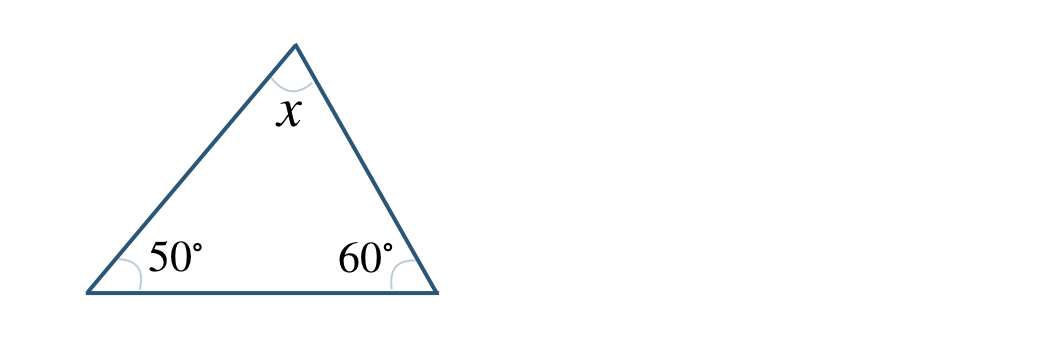
②
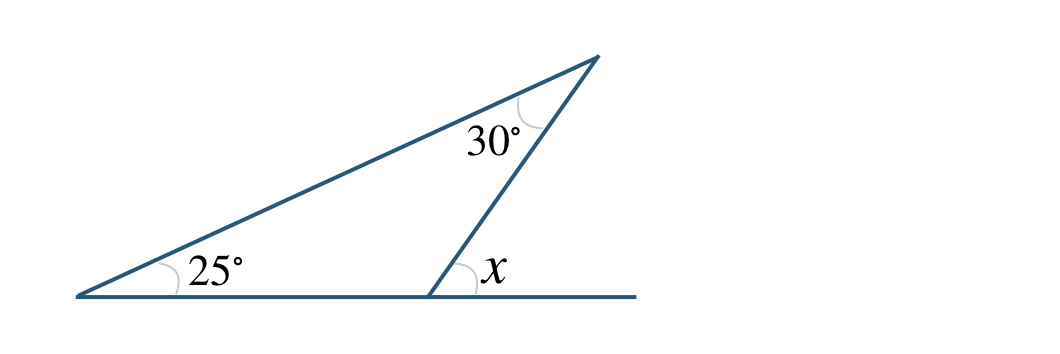
③
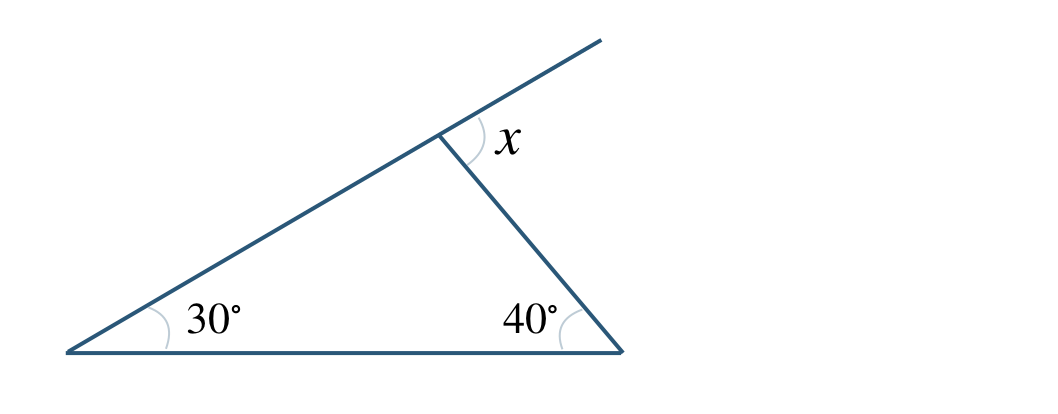
④
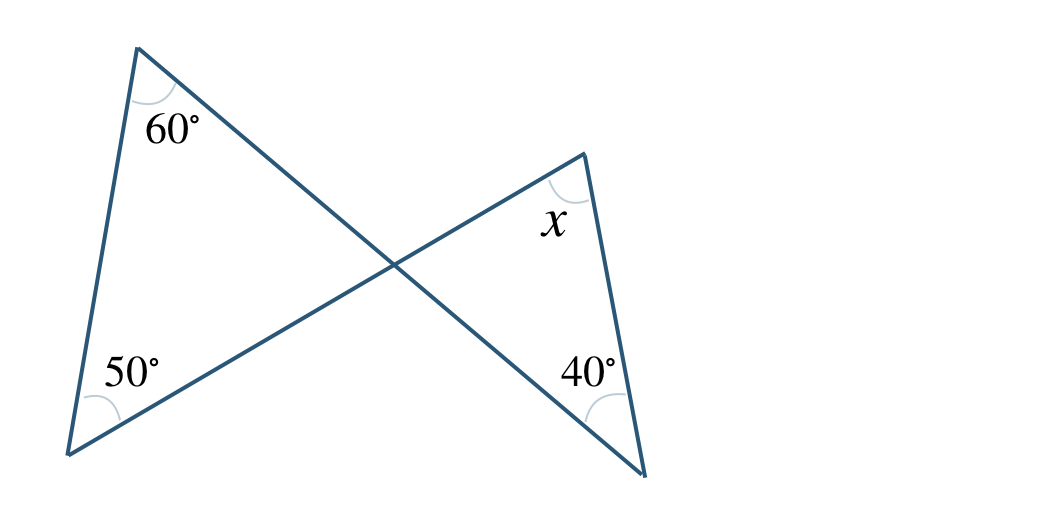
⑤
\({\small (2)}~\)三角形の2つの内角が次のとき、鋭角三角形、直角三角形、鈍角三角形のどれとなるか答えよ。
① \(20^\circ~,~70^\circ\)
② \(40^\circ~,~60^\circ\)
③ \(20^\circ~,~30^\circ\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(\angle x=70^\circ\)
② \(\angle x=55^\circ\)
③ \(\angle x=70^\circ\)
④ \(\angle x=70^\circ\)
⑤ \(\angle x=90^\circ\)
\({\small (2)}~\)
① 直角三角形
② 鋭角三角形
③ 鈍角三角形

多角形の内角と外角
次の問いに答えよ。
\({\small (1)}~\)十角形について、次の値を求めよ。
① 内角の和。
② 外角の和。
\({\small (2)}~\)正十二角形について、次の値を求めよ。
① 内角の和。
② 外角の和。
③ 1つの内角の大きさ。
④ 1つの外角の大きさ。
\({\small (3)}~\)次の条件の多角形を答えよ。
① 内角の和が \(1620^\circ\)。
② 1つの内角が \(135^\circ\) の正多角形。
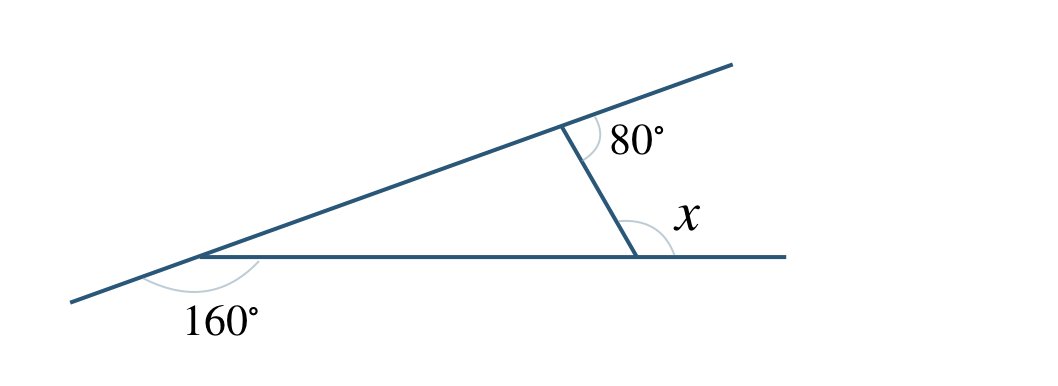
\({\small (4)}~\)次の図において、\(\angle x\) の大きさを求めよ。
①
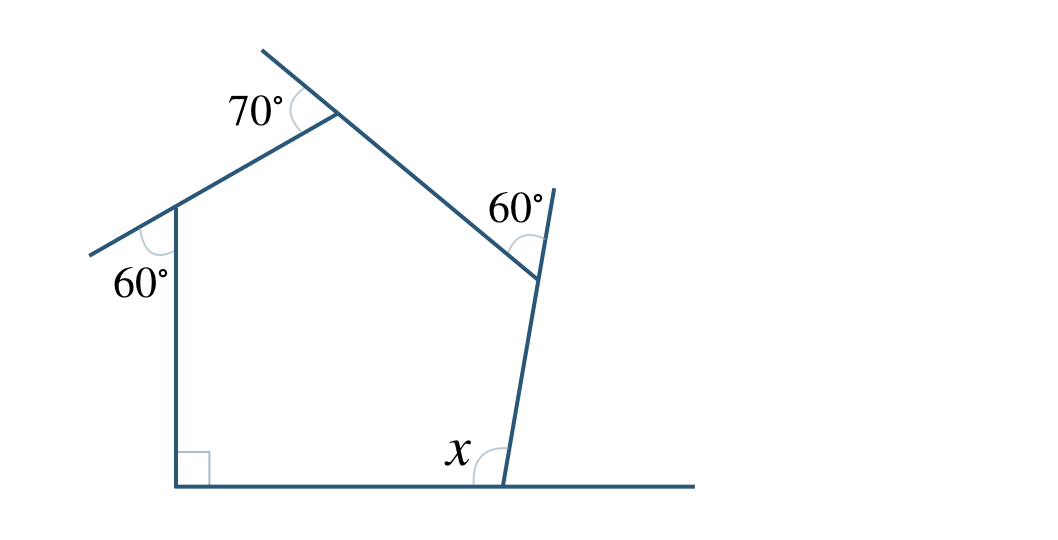
②
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(1440^\circ\) ② \(360^\circ\)
\({\small (2)}~\)
① \(1800^\circ\) ② \(360^\circ\)
③ \(150^\circ\) ④ \(30^\circ\)
\({\small (3)}~\)
① 十一角形 ② 正八角形
\({\small (4)}~\)
① \(\angle x=120^\circ\) ② \(\angle x=100^\circ\)

合同な図形の表し方
次の問いに答えよ。
\({\small (1)}~\)三角形 \({\rm ABC}\) と三角形 \({\rm DEF}\) が合同である。
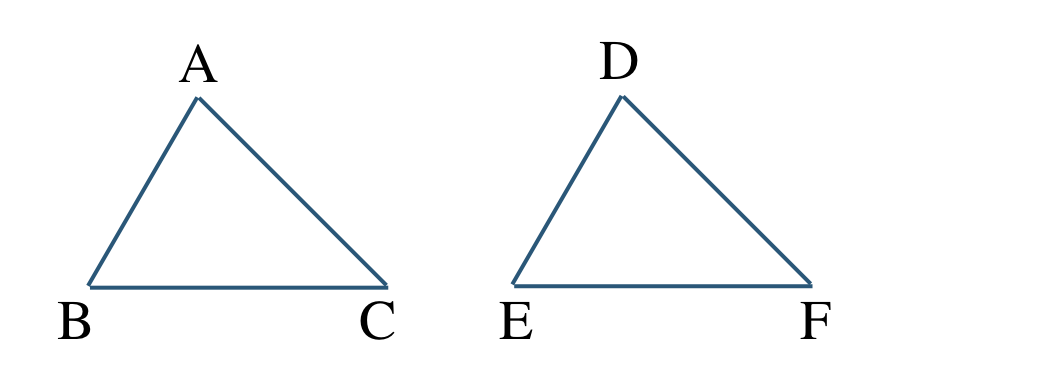
① 合同であることを記号で表せ。
② 等しい線分の長さを記号で表せ。
③ 等しい角の大きさを記号で表せ。
\({\small (2)}~\)次の2つの四角形は合同である。
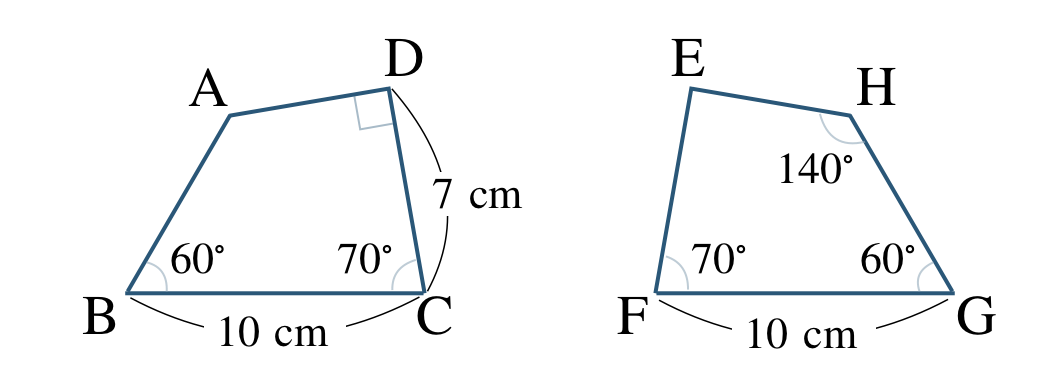
① 合同であることを記号で表せ。
② \(\angle {\rm A}\) の大きさを求めよ。
③ \(\angle {\rm E}\) の大きさを求めよ。
④ 線分 \({\rm EF}\) の長さを求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(\triangle {\rm ABC}\equiv \triangle {\rm DEF}\)
② \({\rm AB=DE~,~BC=EF~,~AC=DF}\)
③ \({\rm \angle A=\angle D~,~\angle B=\angle E~,~\angle C=\angle F}\)
\({\small (2)}~\)
① 四角形 \( {\rm ABCD}\equiv\) 四角形 \({\rm HGFE}\)
② \(\angle {\rm A}=140^\circ\)
③ \(\angle {\rm E}=90^\circ\)
④ \({\rm EF}=7~{\rm cm}\)

三角形の合同条件
次の問いに答えよ。
\({\small (1)}~\)次の図において、合同な図形を見つけて記号 \(\equiv\) で表し、合同条件を答えよ。
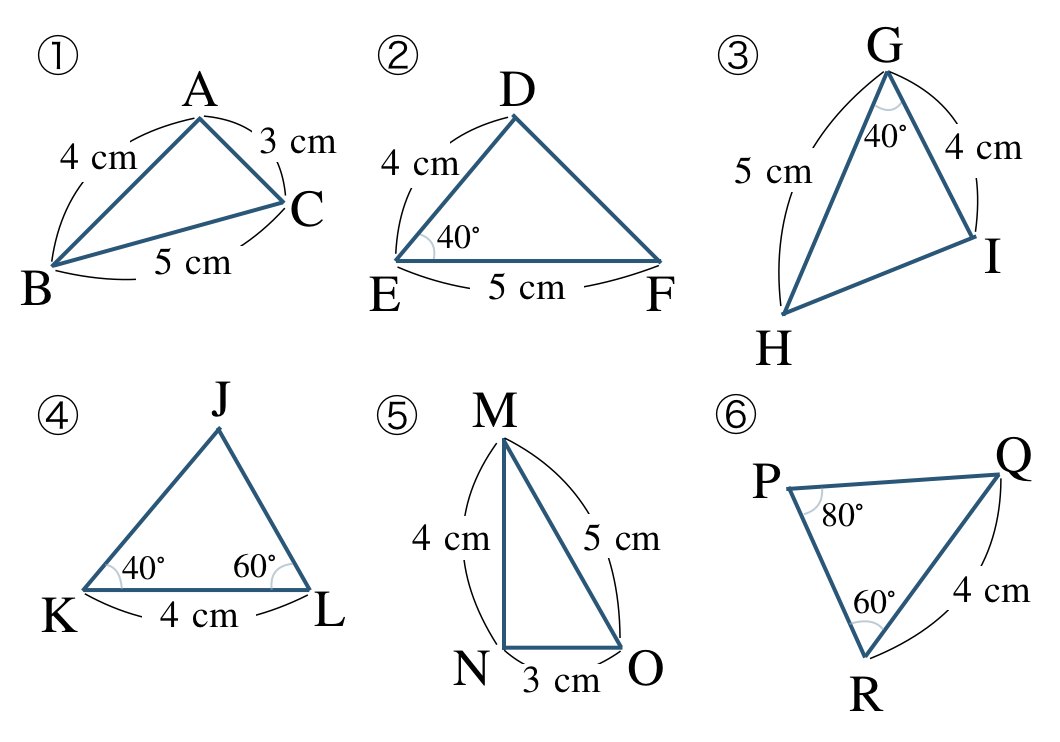
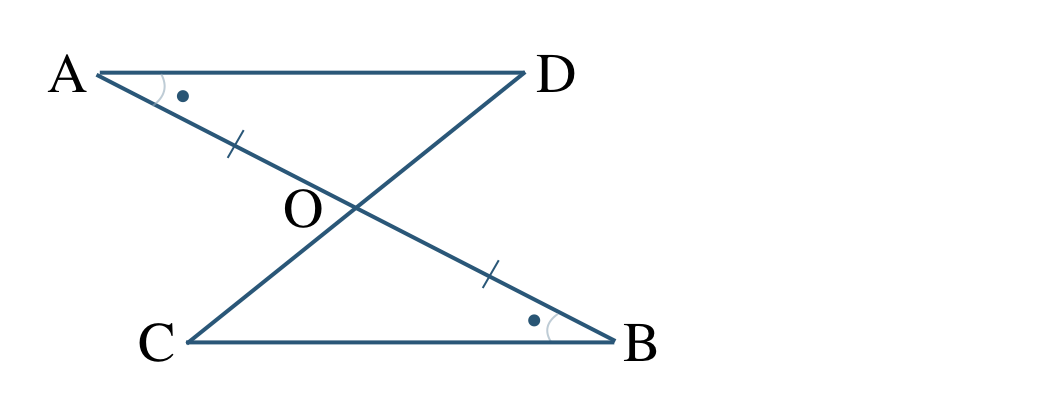
\({\small (2)}~\)次の図において、合同な三角形を見つけて記号 \(\equiv\) で表し、合同条件を答えよ。ただし、それぞれの図形で同じ記号のついた辺や角は等しいとする。
①
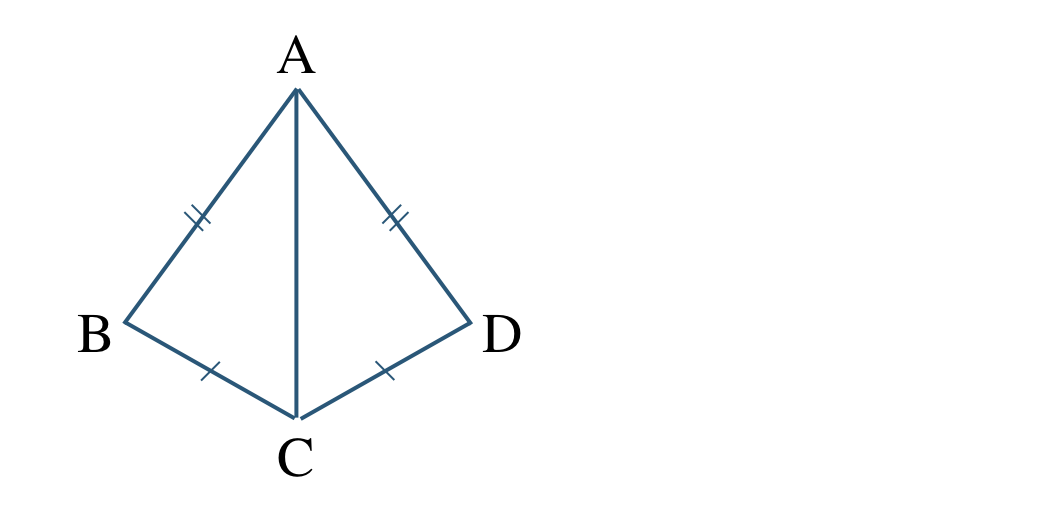
②
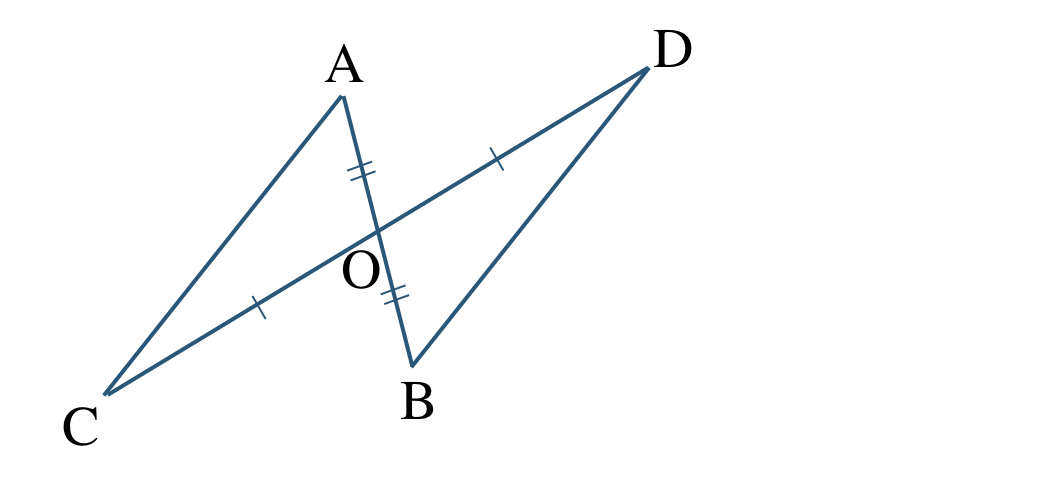
③
[ 解答を見る ]
【解答】
\({\small (1)}~\)
①と⑤、\(\triangle {\rm ABC}\equiv \triangle {\rm NMO}\)
3組の辺がそれぞれ等しい
②と③、\(\triangle {\rm DEF}\equiv \triangle {\rm IGH}\)
2組の辺とその間の角がそれぞれ等しい
④と⑥、\(\triangle {\rm JKL}\equiv \triangle {\rm PQR}\)
1組の辺とその両端の角がそれぞれ等しい
\({\small (2)}~\)
① \(\triangle {\rm ABC}\equiv \triangle {\rm ADC}\)
3組の辺がそれぞれ等しい
② \(\triangle {\rm AOC}\equiv \triangle {\rm BOD}\)
2組の辺とその間の角がそれぞれ等しい
③ \(\triangle {\rm AOD}\equiv \triangle {\rm BOC}\)
1組の辺とその両端の角がそれぞれ等しい

仮定と結論
次のことがらについて、仮定と結論をそれぞれ答えよ。
\({\small (1)}~\)\(\triangle {\rm ABC}\equiv \triangle {\rm DEF}\) ならば、\({\rm AB=DF}\)
\({\small (2)}~\)\(l\,//\,m~,~m\,//\,n\) ならば、\(l\,//\,n\)
\({\small (3)}~\)\(x\) が \(10\) の倍数ならば、\(x\) は \(2\) の倍数である
\({\small (4)}~\)三角形の内角の和は \(180^\circ\) である
[ 解答を見る ]
【解答】
\({\small (1)}~\)仮定:\(\triangle {\rm ABC}\equiv \triangle {\rm DEF}\)
結論:\({\rm AB=DF}\)
\({\small (2)}~\)仮定:\(l\,//\,m~,~m\,//\,n\)
結論:\(l\,//\,n\)
\({\small (3)}~\)仮定:\(x\) が \(10\) の倍数
結論:\(x\) は \(2\) の倍数
\({\small (4)}~\)仮定:三角形
結論:内角の和は \(180^\circ\)

三角形の合同の証明
次の問いに答えよ。
\({\small (1)}~\)次のことの根拠となることがらを説明せよ。
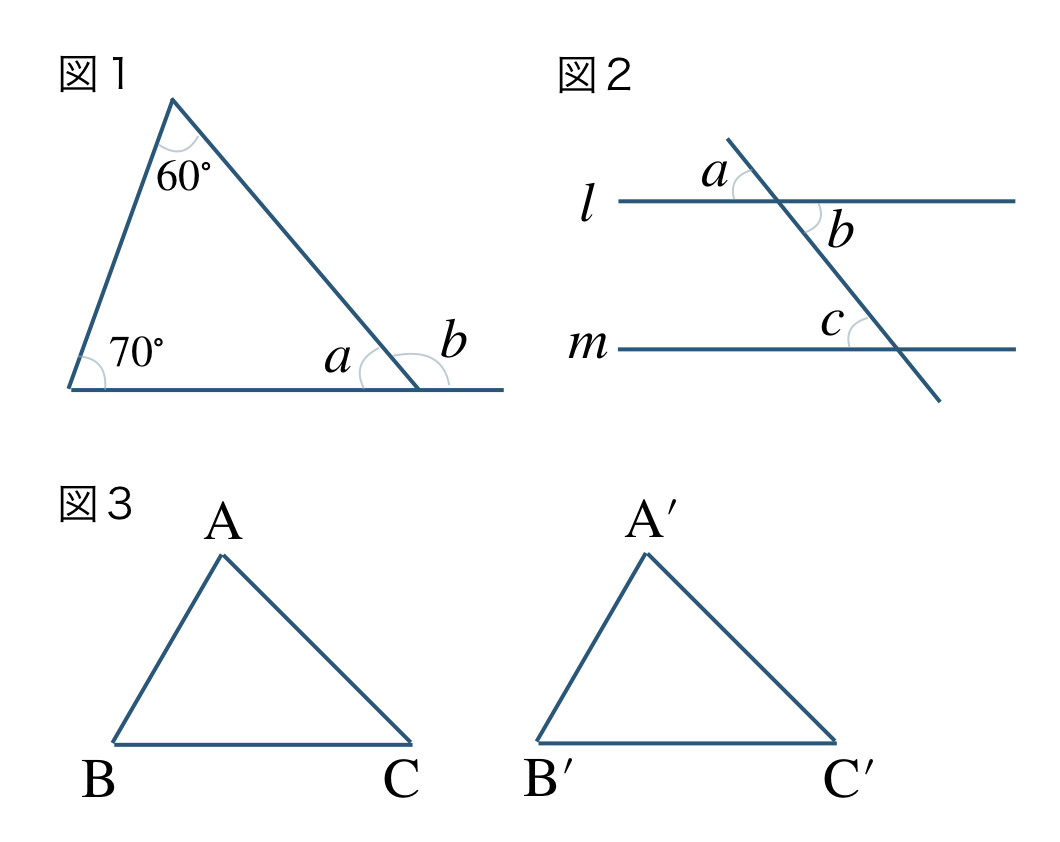
① 図1で、\(\angle a=50^\circ\)
② 図1で、\(\angle b=130^\circ\)
③ 図2で、\(\angle a=\angle b\)
④ 図2で、\(l\,//\,m\) ならば \(\angle a=\angle c\)
⑤ 図2で、\(l\,//\,m\) ならば \(\angle b=\angle c\)
⑥ 図2で、\(\angle a=\angle c\) ならば \(l\,//\,m\)
⑦ 図2で、\(\angle b=\angle c\) ならば \(l\,//\,m\)
⑧ 図3で、
\(\triangle {\rm ABC}\equiv\triangle {\rm A’B’C’}\) ならば \({\rm AB=A’B’}\)
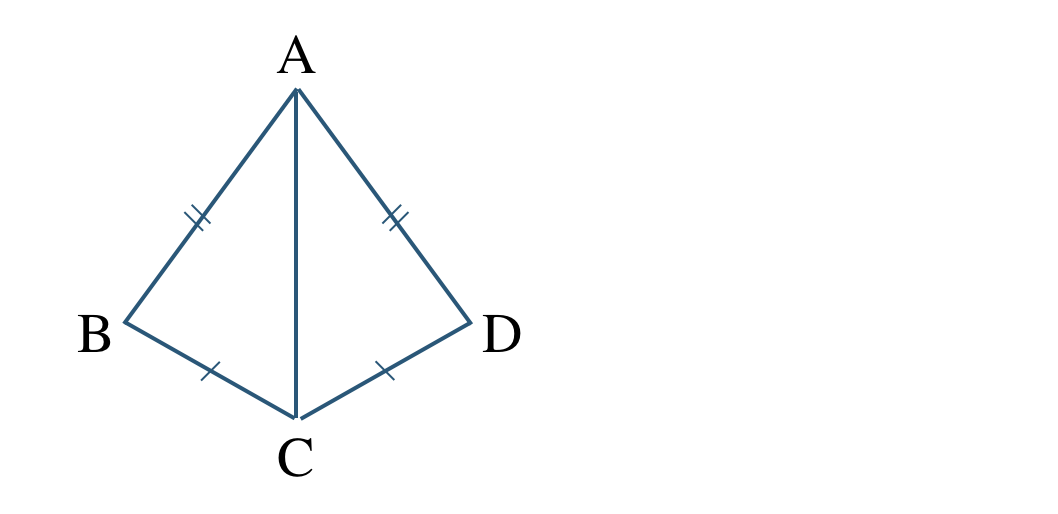
\({\small (2)}~\)次の図で \(\triangle {\rm ABC}\) と \(\triangle {\rm ADC}\) が合同であることを証明せよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① 三角形の内角の和は \(180^\circ\) である
② 三角形の外角は、それととなり合わない2つの内角の和に等しい
③ 対頂角が等しい
④ 2直線が平行ならば、同位角は等しい
⑤ 2直線が平行ならば、錯角は等しい
⑥ 同位角が等しければ、その2直線は平行である
⑦ 錯角が等しければ、その2直線は平行である
⑧ 合同な図形では、対応する線分や角は等しい
\({\small (2)}~\)
[証明] \(\triangle {\rm ABC}\) と \(\triangle {\rm ADC}\) において、
仮定より、
\({\rm AB=AD}~~~\cdots{\large ①}\)
\({\rm BC=DC}~~~\cdots{\large ②}\)
また、共通の辺から、
\({\rm AC=AC}~~~\cdots{\large ③}\)
①、②、③より、
3組の辺がそれぞれ等しいから、
\(\triangle {\rm ABC}\equiv\triangle {\rm ADC}\)
[終]

図形の性質と証明
次の証明をせよ。
\({\small (1)}~\)次の図において、
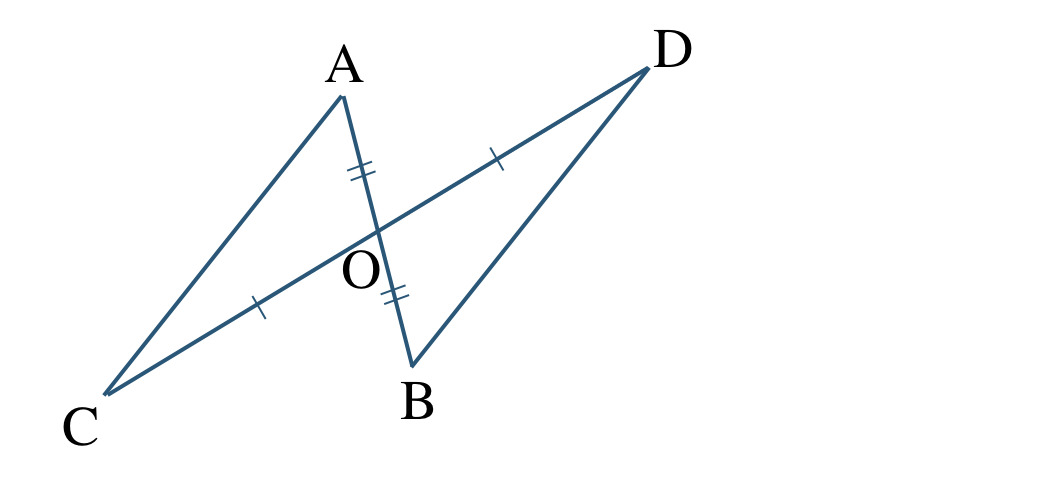
\({\rm AO=BO~,~CO=DO}\) ならば \({\rm AC\,//\,DB}\)
\({\small (2)}~\)次の図において、
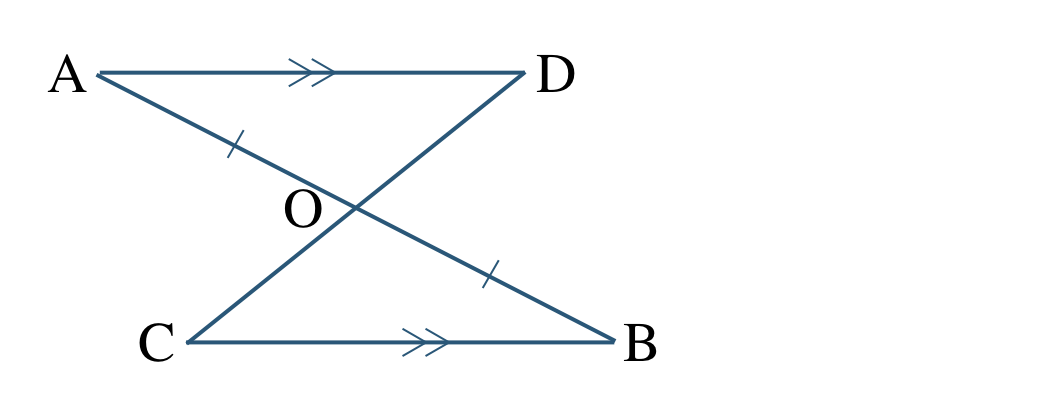
\({\rm AO=BO~,~AD\,//\,CB}\) ならば \({\rm AD=CB}\)
\({\small (3)}~\)角の二等分線の作図において、
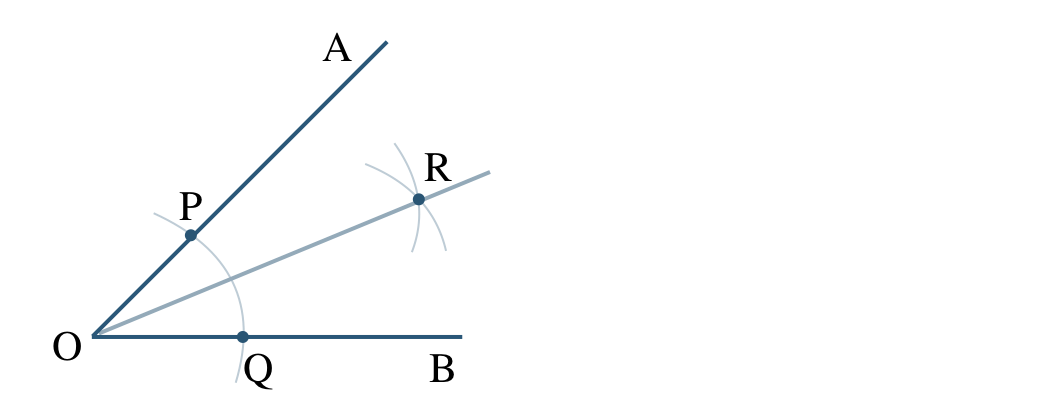
半直線 \({\rm OR}\) が \(\angle {\rm AOB}\) を二等分する
[ 解答を見る ]
【解答】
\({\small (1)}~\)
[証明] \(\triangle {\rm ACO}\) と \(\triangle {\rm BDO}\) において、
仮定より、
\({\rm AO=BO}~~~\cdots{\large ①}\)
\({\rm CO=DO}~~~\cdots{\large ②}\)
また、対頂角から、
\(\angle{\rm AOC}=\angle{\rm BOD}~~~\cdots{\large ③}\)
①、②、③より、
2組の辺とその間の角がそれぞれ等しいから、
\(\triangle {\rm ACO}\equiv\triangle {\rm BDO}\)
合同な図形では対応する角の大きさは等しいから、
\(\angle{\rm ACO}=\angle{\rm BDO}\)
錯角が等しいから、
\({\rm AC\,//\,DB}\)
[終]
\({\small (2)}~\)
[証明] \(\triangle {\rm AOD}\) と \(\triangle {\rm BOD}\) において、
仮定より、
\({\rm AO=BO}~~~\cdots{\large ①}\)
\({\rm AD\,//\,CB}\) より錯角が等しいから、
\(\angle{\rm DAO}=\angle{\rm CBO}~~~\cdots{\large ②}\)
また、対頂角から、
\(\angle{\rm AOD}=\angle{\rm BOC}~~~\cdots{\large ③}\)
①、②、③より、
1組の辺とその両端の角がそれぞれ等しいから、
\(\triangle {\rm AOD}\equiv\triangle {\rm BOD}\)
合同な図形では対応する辺の長さは等しいから、
\({\rm AD=CB}\)
[終]
\({\small (3)}~\)
[証明] \(\triangle {\rm POR}\) と \(\triangle {\rm QOR}\) において、
仮定より、点 \({\rm O}\) を中心とした円と半直線 \({\rm OA~,~OB}\) の交点が \({\rm P~,~Q}\) より、
\({\rm OP=OQ}~~~\cdots{\large ①}\)
点 \({\rm P~,~Q}\) を中心とした同じ半径の円の交点が \({\rm R}\) より、
\({\rm PR=QR}~~~\cdots{\large ②}\)
また、共通の辺から、
\({\rm OR=OR}~~~\cdots{\large ③}\)
①、②、③より、
3組の辺がそれぞれ等しいから、
\(\triangle {\rm POR}\equiv\triangle {\rm QOR}\)
合同な図形では対応する角の大きさは等しいから、
\(\angle{\rm POR}=\angle{\rm QOR}\)
これより、
\(\angle{\rm AOR}=\angle{\rm BOR}\)
したがって、半直線 \({\rm OR}\) が \(\angle {\rm AOB}\) を二等分する
[終]



