このページは「中学数学3 関数y=ax²」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう!
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
【問題一覧】中学数学3 関数y=ax²
2乗に比例する関数
次の問いに答えよ。
\({\small (1)}~\)次の①〜④のそれぞれで \(y\) を \(x\) の式で表し、\(y\) が \(x\) の2乗に比例するものを答えよ。
① 1辺 \(x~{\rm cm}\) の立方体の表面積 \(y~{\rm cm}^2\) 。
② 1辺 \(x~{\rm cm}\) の立方体の体積 \(y~{\rm cm}^3\) 。
③ 半径 \(x~{\rm cm}\) の円の円周の長さ \(y~{\rm cm}\) 。
④ 半径 \(x~{\rm cm}\) の円の面積 \(y~{\rm cm}^2\) 。
\({\small (2)}~\)底辺 \(x~{\rm cm}\)、高さ \(x~{\rm cm}\) の三角形の面積を 半径 \(y~{\rm cm}^2\) とするとき、\(y\) を \(x\) の式で表し、次の表を完成させよ。
| \(x~{\rm cm}\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(y~{\rm cm}^2\) |
[ 解答を見る ]
【解答】
\({\small (1)}~\)
\(~~{\large ①}~y=6x^2\) \(y\) が \(x\) の2乗に比例する
\(~~{\large ②}~y=x^3\) \(y\) が \(x\) の2乗に比例しない
\(~~{\large ③}~y=2\pi x\) \(y\) が \(x\) の2乗に比例しない
\(~~{\large ④}~y=\pi x^2\) \(y\) が \(x\) の2乗に比例する
\({\small (2)}~\)
\(\begin{split}~~~y=\frac{\,1\,}{\,2\,}x^2\end{split}\)
| \(x~{\rm cm}\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(\begin{split}y~{\rm cm}^2\end{split}\) | \(\begin{split}{\frac{\,1\,}{\,2\,}}\end{split}\) | \(\begin{split}2\end{split}\) | \(\begin{split}{\frac{\,9\,}{\,2\,}}\end{split}\) | \(\begin{split}8\end{split}\) | \(\begin{split}{\frac{\,25\,}{\,2\,}}\end{split}\) | \(\begin{split}18\end{split}\) |

関数y=ax²の式
次の問いに答えよ。
\({\small (1)}~\)\(y\) が \(x\) の2乗に比例し、\(x=2\) のとき \(y=12\) である。このとき \(y\) を \(x\) の式で表せ。また、\(x=-3\) のとき \(y\) の値を求めよ。
\({\small (2)}~\)\(y\) が \(x\) の2乗に比例し、\(x=2\) のとき \(y=2\) である。このとき \(y\) を \(x\) の式で表せ。また、\(x=6\) のとき \(y\) の値を求めよ。
\({\small (3)}~\)\(y\) が \(x\) の2乗に比例し、\(x=3\) のとき \(y=-45\) である。このとき \(y\) を \(x\) の式で表せ。また、\(x=-2\) のとき \(y\) の値を求めよ。
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~y=3x^2~~,~y=27\end{split}\)
\(\begin{split}{\small (2)}~y=\frac{\,1\,}{\,2\,}x^2~~,~y=18\end{split}\)
\(\begin{split}{\small (3)}~y=-5x^2~~,~y=-20\end{split}\)

関数y=ax²のグラフ
次の問いに答えよ。
\({\small (1)}~\)\(y=x^2\) のグラフを参考にして、\(y=2x^2\) のグラフをかけ。
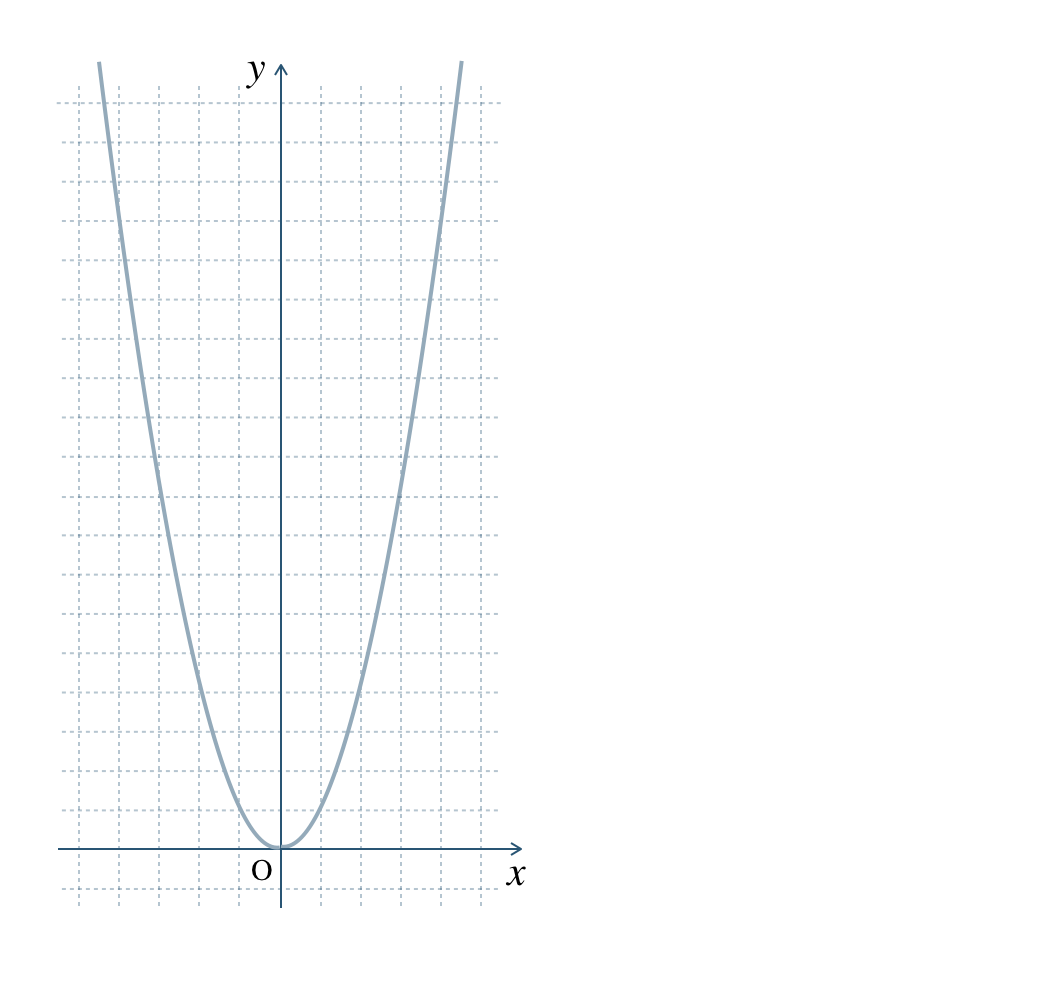
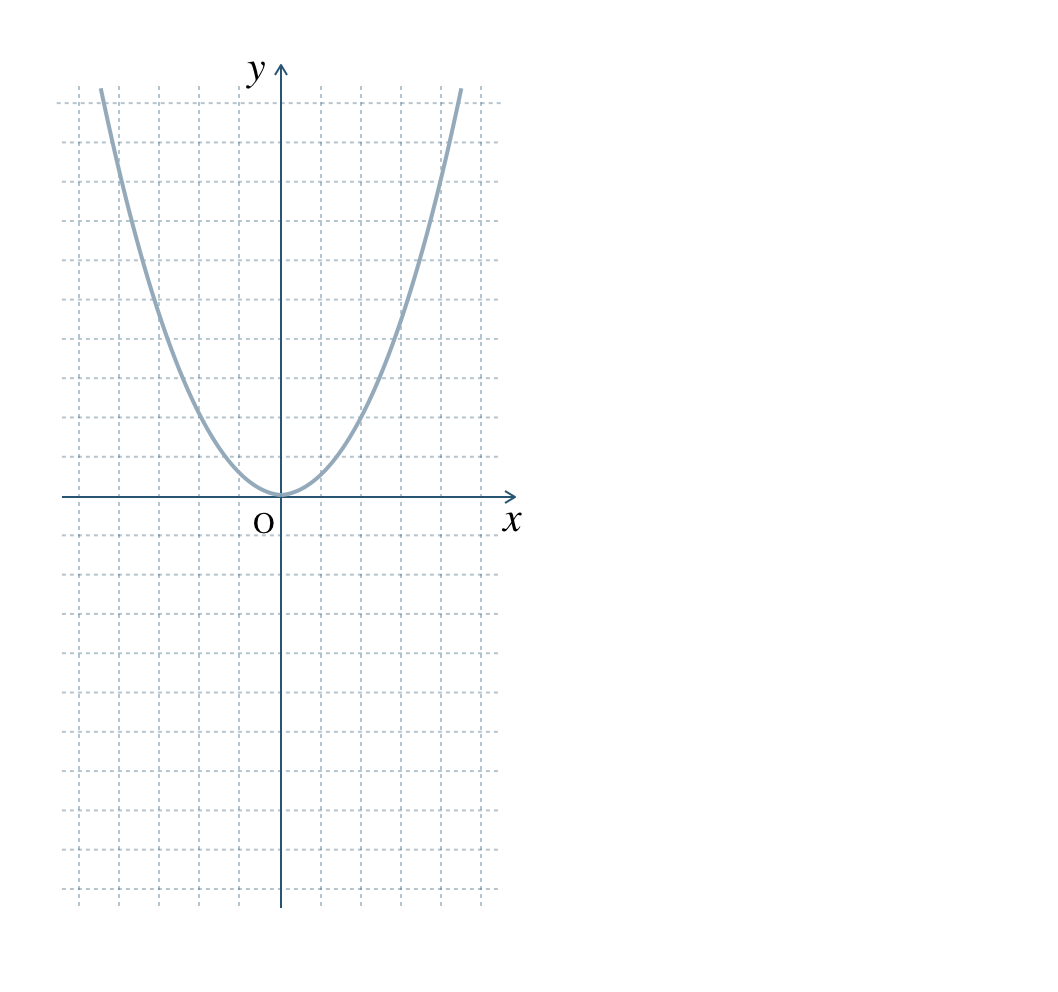
\({\small (2)}~\)\(\begin{split}y={\frac{\,1\,}{\,2\,}}x^2\end{split}\) のグラフを参考にして、
\(\begin{split}y=-{\frac{\,1\,}{\,2\,}}x^2\end{split}\) のグラフをかけ。
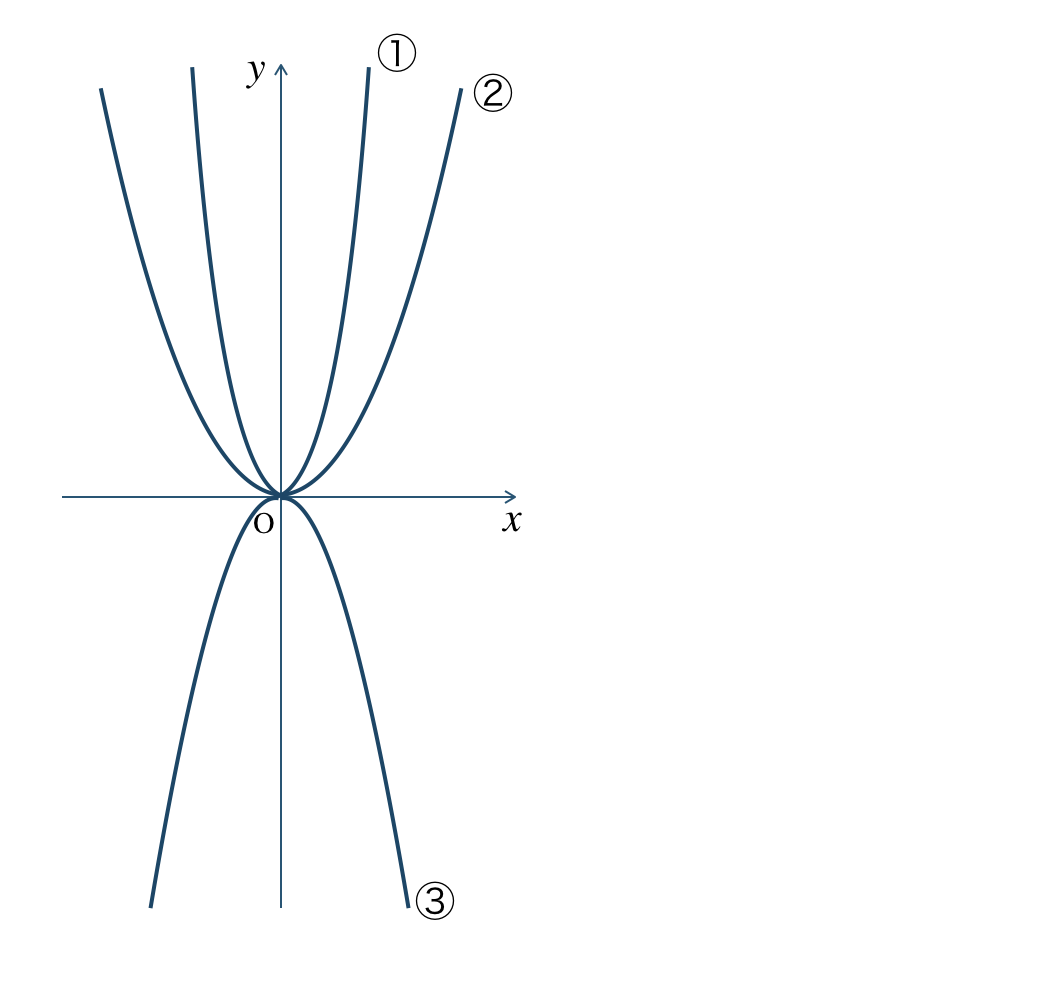
\({\small (3)}~\)次の図の①〜③のグラフは、次のどの関数となるか選べ。
\(\begin{split}~~~y=x^2~,~y=3x^2~,~y=-2x^2\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)
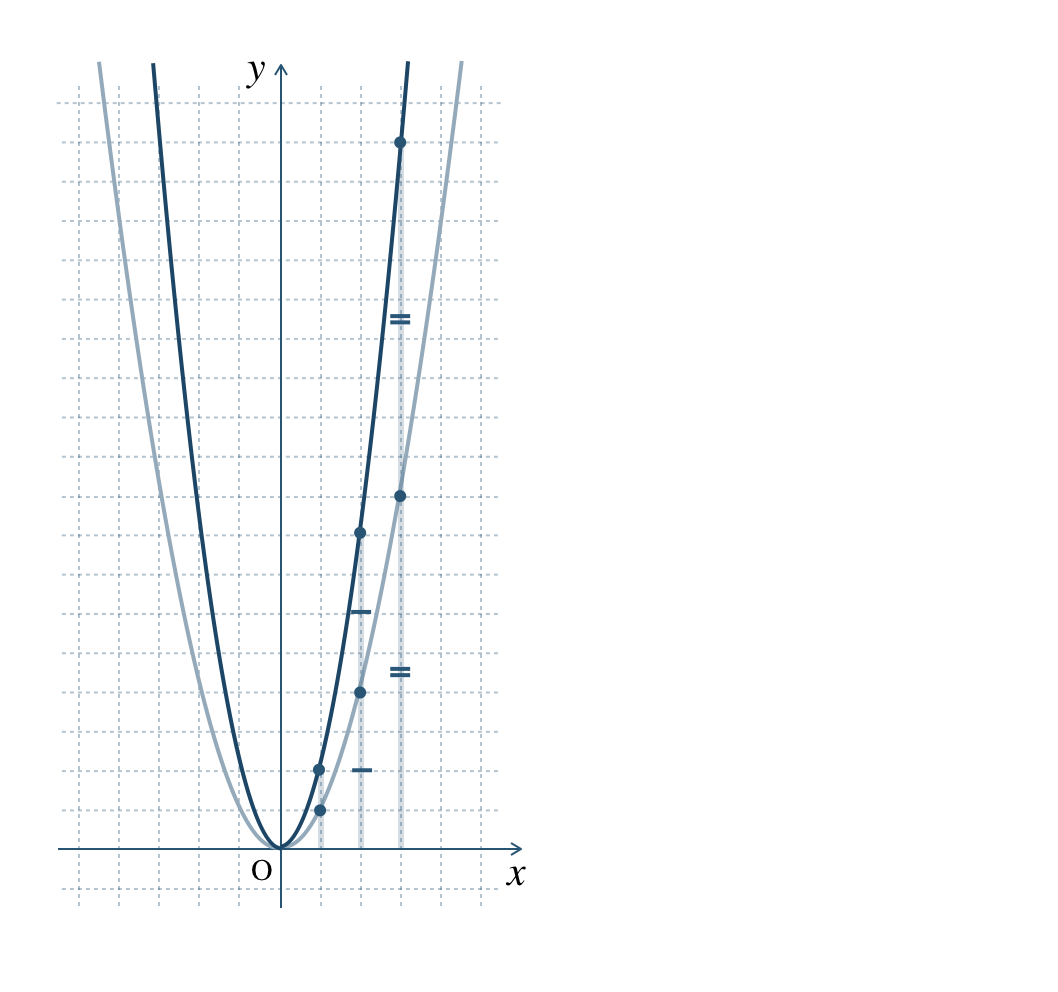
\({\small (2)}~\)
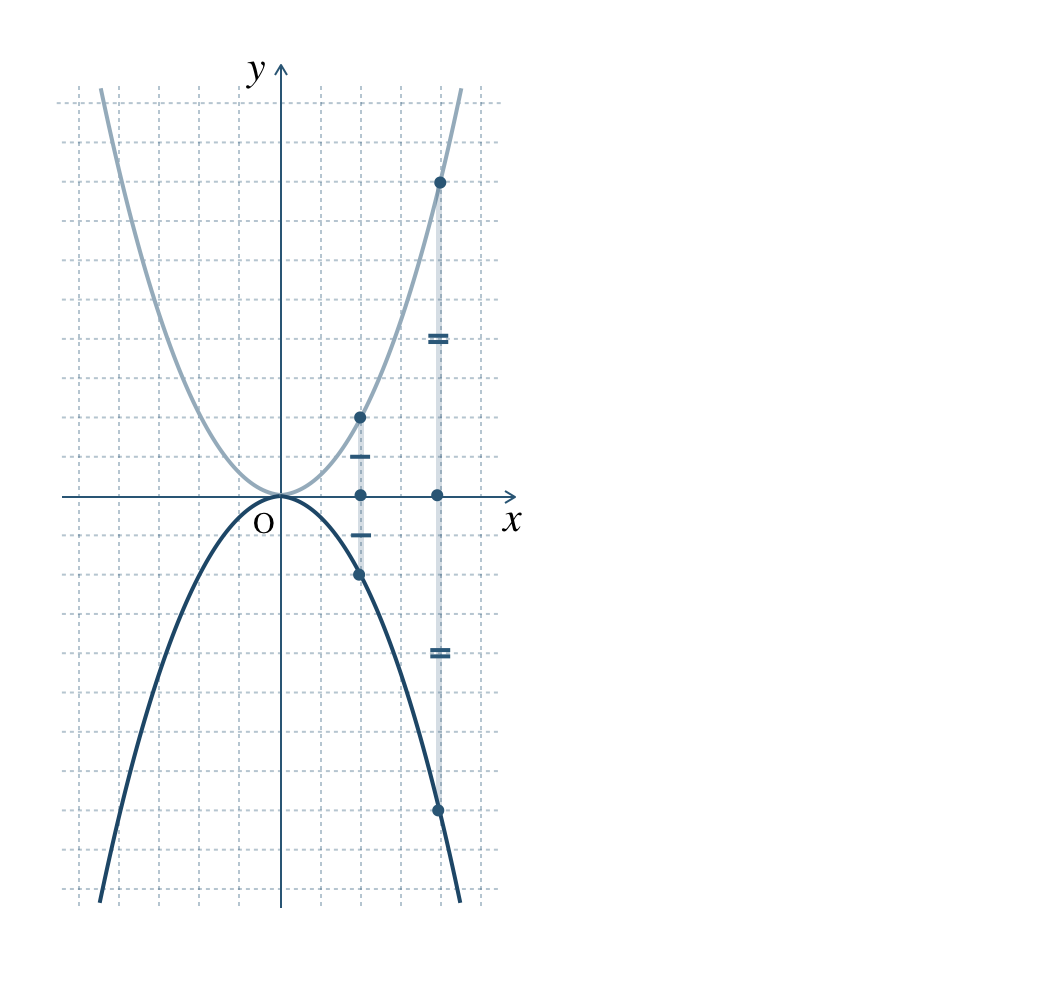
\({\small (3)}~\)
① \(y=3x^2\) ② \(y=x^2\) ③ \(y=-2x^2\)

関数y=ax²と変域
次の問いに答えよ。
\({\small (1)}~\)関数 \(y=x^2\) について、\(x\) の変域が
次のとき、\(y\) の増減と \(y\) の変域を求めよ。
① \(\begin{split}1≦x≦2\end{split}\)
② \(\begin{split}-3≦x≦1\end{split}\)
\({\small (2)}~\)関数 \(\begin{split}y=-{\frac{\,1\,}{\,2\,}}x^2\end{split}\) について、\(x\) の変域が
次のとき、\(y\) の増減と \(y\) の変域を求めよ。
① \(\begin{split}-4≦x≦-2\end{split}\)
② \(\begin{split}-1≦x≦4\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(\begin{split}1≦y≦4\end{split}\)
② \(\begin{split}0≦y≦9\end{split}\)
\({\small (2)}~\)
① \(\begin{split}-8≦y≦-2\end{split}\)
② \(\begin{split}-8≦y≦0\end{split}\)

関数y=ax²の変化の割合
次の問いに答えよ。
\({\small (1)}~\)関数 \(y=x^2\) について、\(x\) の値が次のように変化するときの変化の割合を求めよ。
① \(1\) から \(3\) まで増加
② \(-4\) から \(-1\) まで増加
\({\small (2)}~\)関数 \(y=-2x^2\) について、\(x\) の値が次のように変化するときの変化の割合を求めよ。
① \(2\) から \(5\) まで増加
② \(-3\) から \(0\) まで増加
[ 解答を見る ]
【解答】
\({\small (1)}~\)① \(4\) ② \(-5\)
\({\small (2)}~\)① \(-14\) ② \(6\)

関数y=ax²と平均の速さ
斜面を転がるボールについて、転がり始めて \(x\) 秒間に転がった距離を \(y~{\rm m}\) とすると、\(x\) と \(y\) の関係が \(y=2x^2\) となった。次のときの平均の速さを求めよ。
\({\small (1)}~\)\(1\) 秒後から \(2\) 秒後まで
\({\small (2)}~\)\(2\) 秒後から \(4\) 秒後まで
\({\small (3)}~\)転がり始めてから \(3\) 秒後まで
[ 解答を見る ]
【解答】
\({\small (1)}~\)秒速 \(6~{\rm m}\)
\({\small (2)}~\)秒速 \(12~{\rm m}\)
\({\small (3)}~\)秒速 \(6~{\rm m}\)

関数y=ax²と制動距離
時速 \(60~{\rm km}\) で走る自動車がブレーキをかけたところ、ブレーキがきき始めて \(18~{\rm m}\) 走って停止した。これを制動距離という。次の問いに答えよ。
\({\small (1)}~\)自動車が時速 \(x~{\rm km}\) で走っているときの制動距離が \(y~{\rm m}\) とすると、\(y\) は \(x\) の2乗に比例する関数となる。\(y\) を \(x\) の式で表せ。
\({\small (2)}~\)時速 \(80~{\rm km}\) のときの制動距離を求めよ。
\({\small (3)}~\)時速 \(100~{\rm km}\) のときの制動距離を求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)\(\begin{split}y=\frac{\,1\,}{\,200\,}x^2\end{split}\)
\({\small (2)}~\)制動距離 \(32~{\rm m}\)
\({\small (3)}~\)制動距離 \(50~{\rm m}\)

関数y=ax²と図形
下の図のように、直角二等辺三角形 \(\triangle {\rm ABC}\) と正方形 \({\rm PQRS}\) が直線 \(l\) 上に並んでいて、点 \({\rm C}\) と点 \({\rm Q}\) が重なっている。
\(\triangle {\rm ABC}\) が直線 \(l\) にそって右方向に毎秒 \(1~{\rm cm}\) の速さで点 \({\rm C}\) が点 \({\rm R}\) と重なるまで動く。
\(\triangle {\rm ABC}\) が動きはじめて \(x\) 秒後の \(\triangle {\rm ABC}\) と正方形 \({\rm PQRS}\) が重なってできる部分の面積を \(y~{\rm cm}^2\) とする。
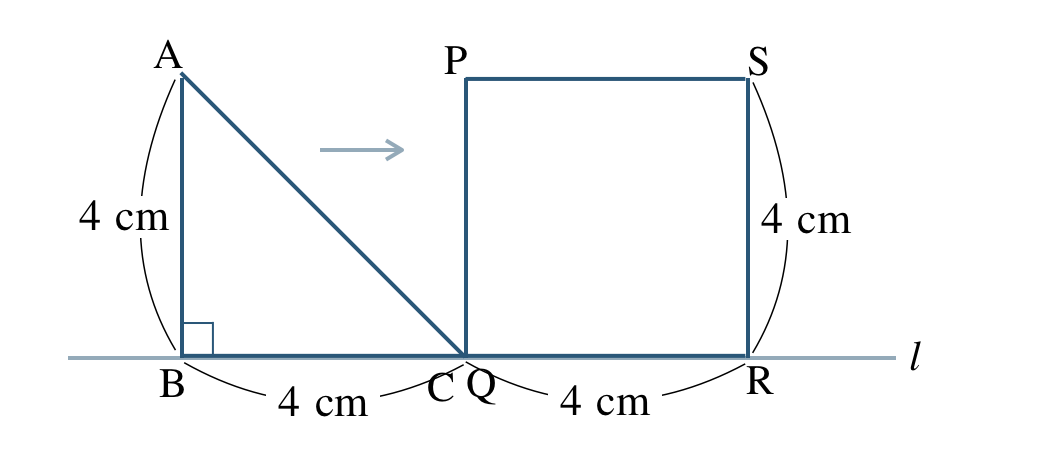
\({\small (1)}~\)\(y\) を \(x\) の式で表して、\(x\) の変域を答えよ。
\({\small (2)}~\)\(x\) と \(y\) の関係をクラブで表せ。
\({\small (3)}~\)\(3\) 秒後の重なって部分の面積 \({\rm cm}^2\) を求めよ。
\({\small (4)}~\)重なって部分の面積 \(4~{\rm cm}^2\) となるのは何秒後が答えよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)\(\begin{split}y=\frac{\,1\,}{\,2\,}x^2~~(0≦x≦4)\end{split}\)
\({\small (2)}~\)
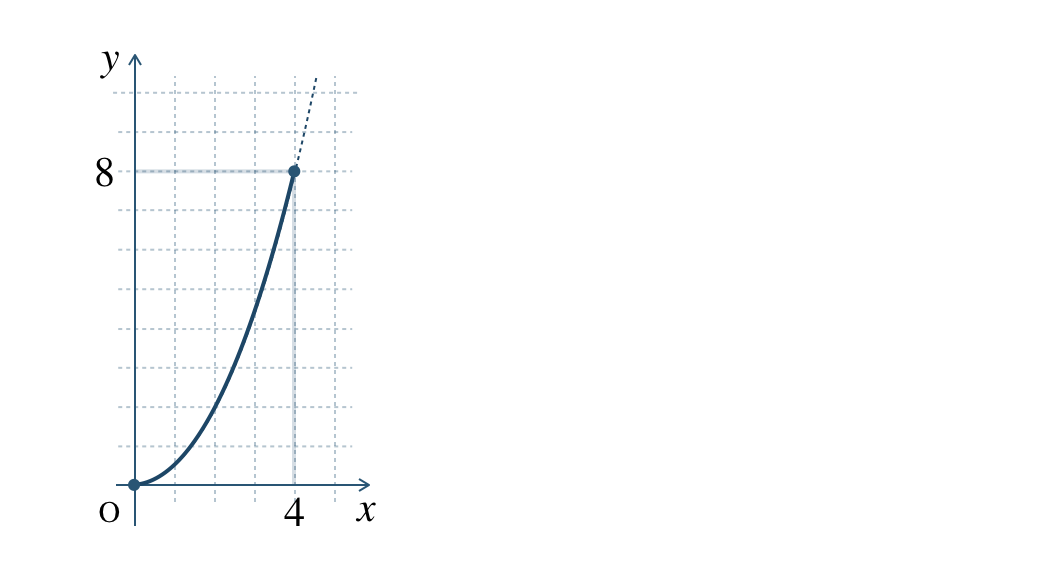
\({\small (3)}~\)面積 \(\begin{split}{\frac{\,9\,}{\,2\,}}~{\rm cm}^2\end{split}\)
\({\small (4)}~\)\(2\sqrt{2}\) 秒後

放物線と直線
関数 \(y=x^2\) のグラフが直線 \(l\) と2点 \({\rm A~,~B}\) で交わる。2点 \({\rm A~,~B}\) の \(x\) 座標がそれぞれ \(-2~,~3\) であるとき、次の問いに答えよ。
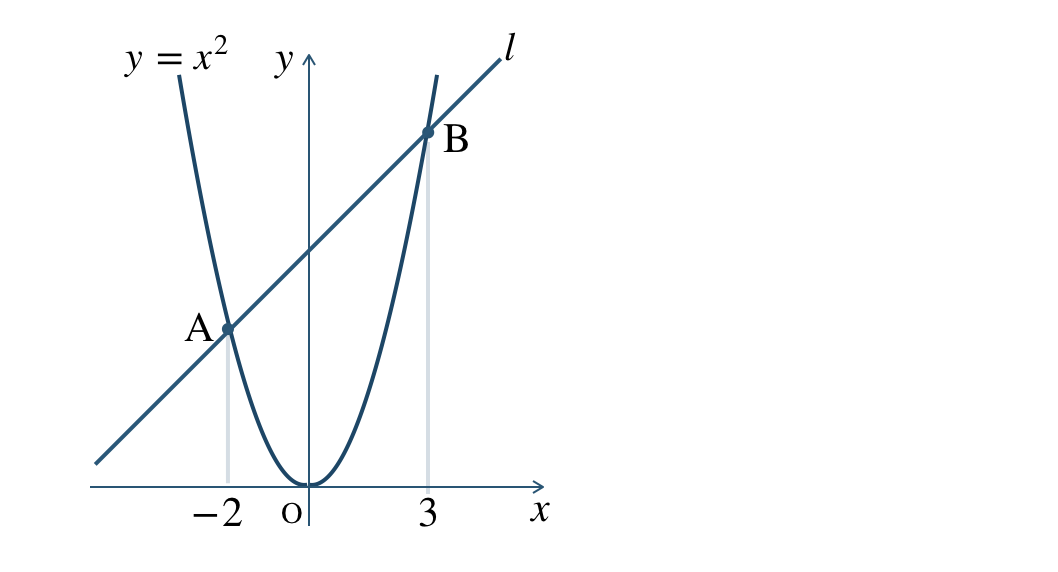
\({\small (1)}~\)2点 \({\rm A~,~B}\) の座標を求めよ。
\({\small (2)}~\)直線 \(l\) の式を求めよ。
\({\small (3)}~\)\(\triangle {\rm OAB}\) の面積を求めよ。
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~{\rm A}(-2~,~4)~,~{\rm B}(3~,~9)\end{split}\)
\(\begin{split}{\small (2)}~y=x+6\end{split}\)
\(\begin{split}{\small (3)}~15\end{split}\)

いろいろな関数
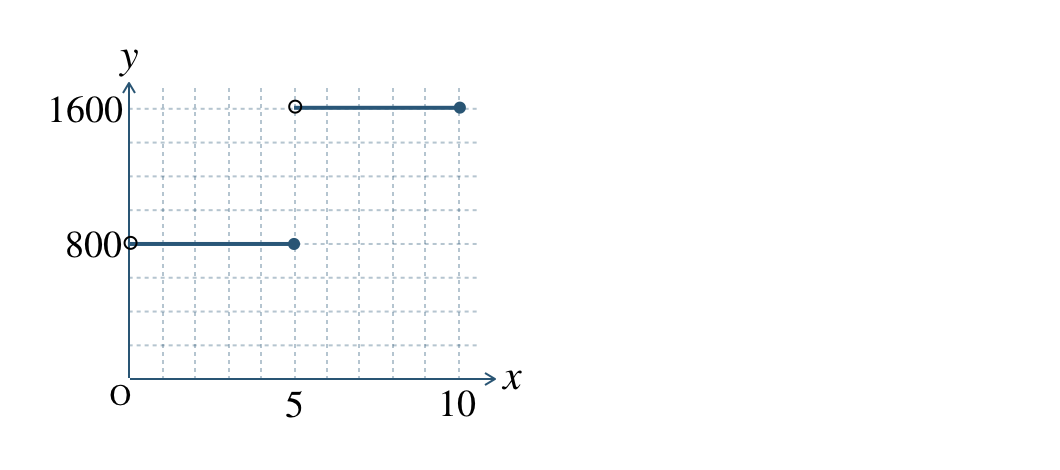
次の表はA社とB社の通信量とその料金の表である。
| A社 | \(\small 5~{\rm GB}\) 以下 | \(\small 10~{\rm GB}\) 以下 |
| 料金 | \(800\) 円 | \(1600\) 円 |
| B社 | \(\small 3~{\rm GB}\) 以下 | \(\small 7~{\rm GB}\) 以下 | \(\small 10~{\rm GB}\) 以下 |
| 料金 | \(500\) 円 | \(1000\) 円 | \(1500\) 円 |
\({\small (1)}~\)A社の通信量 \(x~{\rm GB}\) と料金 \(y\) 円の関係を表すグラフをかけ。
\({\small (2)}~\)B社の通信量 \(x~{\rm GB}\) と料金 \(y\) 円の関係を表すグラフをかけ。
\({\small (3)}~\)次の通信量を使うとき、A社とB社のどちらか安いか答えよ。
① \(2~{\rm GB}\) ② \(4~{\rm GB}\)
③ \(6~{\rm GB}\) ④ \(8~{\rm GB}\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)
\({\small (2)}~\)
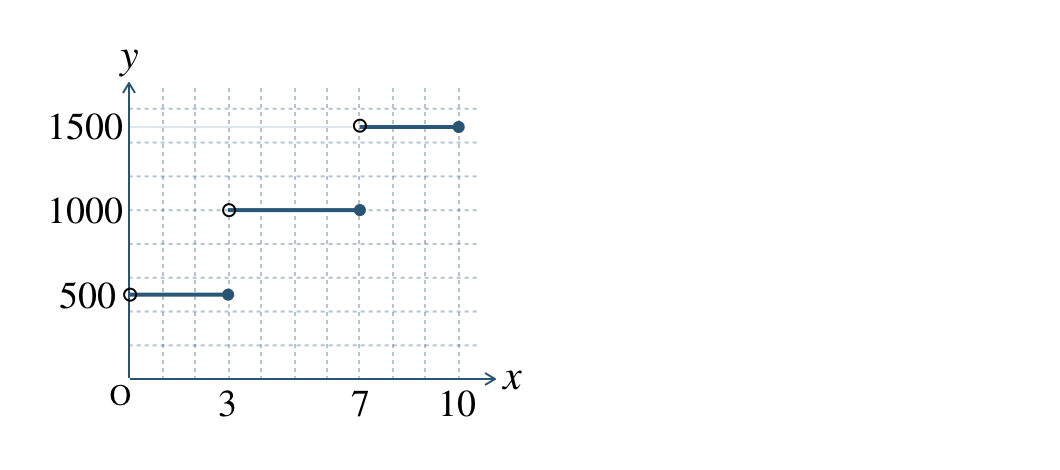
\({\small (3)}~\)
① B社の方が安い
② A社の方が安い
③ B社の方が安い
④ B社の方が安い



