東京書籍：新しい数学３

p.189 問1\(\begin{split}{\small (1)}~x=8\end{split}\)　　\(\begin{split}{\small (2)}~x=5\sqrt{2}\end{split}\)
\(\begin{split}{\small (3)}~x=\sqrt{21}\end{split}\)

p.191 問1\(~~~\)(イ)、(ウ)、(エ)

p.194 問1\(\begin{split}~~~57.6~{\rm m}\end{split}\)

p.195 問2\(\begin{split}{\small (1)}~x=3\sqrt{2}\end{split}\)
\(\begin{split}{\small (2)}~x=8~,~y=4\sqrt{3}\end{split}\)

p.195 問3\(\begin{split}~~~{\rm AB}=\frac{\,16\sqrt{3}\,}{\,3\,}~,~{\rm BC}=\frac{\,8\sqrt{3}\,}{\,3\,}\end{split}\)

---

\(\begin{split}~~~{\rm AD}=4\sqrt{2}~,~{\rm CD}=4\sqrt{2}\end{split}\)

p.195 問4

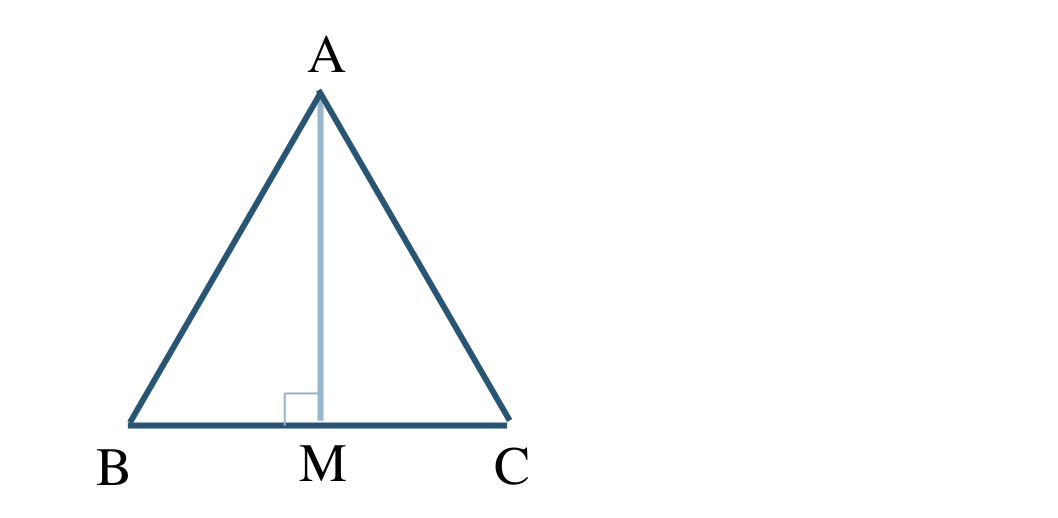
正三角形ＡＢＣの点Ａから辺ＢＣに下ろした垂線をＡＭとする
\(\begin{split}~~~{\rm BM}=\frac{\,a\,}{\,2\,}\end{split}\)
\({\rm BM:AM }=1:\sqrt{3}\) より、
\(\begin{split}~~~{\rm AM}=\frac{\,\sqrt{3}\,}{\,2\,}a\end{split}\)
よって、\(\triangle {\rm ABC}\) の面積 \(S\) は、
\(\begin{split}~~~S=\frac{\,1\,}{\,2\,}\times a\times \frac{\,\sqrt{3}\,}{\,2\,}a=\frac{\,\sqrt{3}\,}{\,4\,} a^2\end{split}\)

p.196 問5\(\begin{split}~~~x=\sqrt{a^2+b^2}\end{split}\)

p.196 問6\(~~~{\rm AH}=\sqrt{7}~{\rm cm}\)　　面積は、\(3\sqrt{7}~{\rm cm}^2\)

p.196 問7\(~~~\)約 \(854~{\rm m}\)

p.197 問8\(\begin{split}{\small (1)}~\sqrt{41}\end{split}\)　　\(\begin{split}{\small (2)}~2\sqrt{10}\end{split}\)

p.198 問9\(\begin{split}~~~2\sqrt{5}~{\rm cm}\end{split}\)

p.198 問10\(\begin{split}~~~4\sqrt{2}~{\rm cm}\end{split}\)

p.199 問11\(\begin{split}~~~5\sqrt{2}~{\rm cm}\end{split}\)

p.199 問12図のように、直方体の頂点をＡ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ、Ｇ、Ｈとする

\(\triangle {\rm FGH}\) は直角三角形で、\({\rm GH}=a~,~{\rm FG}=b\) であるから、
\(\begin{split}~~~{\rm FH}^2=a^2+b^2~~~\cdots{\large ①}\end{split}\)
次に、\(\triangle {\rm BFH}\) も直角三角形で、\({\rm BF}=c\) であるから、
\(\begin{split}~~~{\rm BH}^2={\rm FH}^2+c^2~~~\cdots{\large ②}\end{split}\)
①と②より、
\(\begin{split}~~~~~~{\rm BH}^2=a^2+b^2+c^2\end{split}\)
\(\begin{split}~~~{\rm BH}=\sqrt{a^2+b^2+c^2}\end{split}\)
よって、対角線の長さは \(\sqrt{a^2+b^2+c^2}\) [終]

p.199 問13\(\begin{split}~~~6\sqrt{3}~{\rm cm}\end{split}\)

p.200 問14\(\begin{split}~~~\frac{\,80\,}{\,3\,}\pi~{\rm cm}^3\end{split}\)

p.200 問15\({\small (1)}~{\rm AH}=3\sqrt{2}~{\rm cm}\)

---

\({\small (2)}~{\rm OH}=\sqrt{7}~{\rm cm}\)、体積 \(12\sqrt{7}~{\rm cm}^3\)

p.204 問1\({\small (1)}~\)\(\triangle {\rm FBD}\) は二等辺三角形

---

長方形の対角線より、
\(\begin{split}~~~\angle{\rm ADB}=\angle{\rm DBC}\end{split}\)
また、折り返した角は重なるので、
\(\begin{split}~~~\angle{\rm FBD}=\angle{\rm DBC}\end{split}\)
よって、
\(\begin{split}~~~\angle{\rm FDB}=\angle{\rm FBD}\end{split}\)
これより、二等辺三角形となる

---

\({\small (2)}~{\rm BF}=8-x~{\rm cm}\)
\({\small (3)}~{\rm AF}=3~{\rm cm}~,~{\rm BF}=5~{\rm cm}\)

p.204 問2\(\begin{split}~~~{\rm CF}=\frac{\,7\,}{\,8\,}~{\rm cm}\end{split}\)

p.204 問3\(\begin{split}~~~40~{\rm cm}\end{split}\)