このページは「中学数学1 データの活用」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう!
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
【問題一覧】中学数学1 データの活用
データの代表値と範囲
次のデータは、A市とB市の日ごとの最高気温を値の順に並べたものである。次の問いに答えよ。

\({\small (1)}~\)それぞれの市の最大値と最小値を求めよ。
\({\small (2)}~\)それぞれの市の範囲を求めよ。また、どちらの市が散らばりが大きいか答えよ。
\({\small (3)}~\)それぞれの市の中央値を求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
A市の最大値 \(31.4\) ℃、最小値 \(21.8\) ℃
B市の最大値 \(33.5\) ℃、最小値 \(20.3\) ℃
\({\small (2)}~\)
A市の範囲 \(9.6\)、B市の範囲 \(13.2\)
散らばりが大きいのはB市
\({\small (3)}~\)
A市 \(27.7\) ℃、B市 \(26.4\) ℃

度数分布表とヒストグラム
次のデータは、A市とB市の日ごとの最高気温を値の順に並べたものである。次の問いに答えよ。

\({\small (1)}~\)階級を \(20\) ℃から始めて、階級の幅を \(2\) ℃として、それぞれの市の度数分布表を完成させよ。
\({\small (2)}~\)それぞれの市のヒストグラムをかけ。
\({\small (3)}~\)それぞれの市の度数折れ線をかけ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)


\({\small (2)}~\)
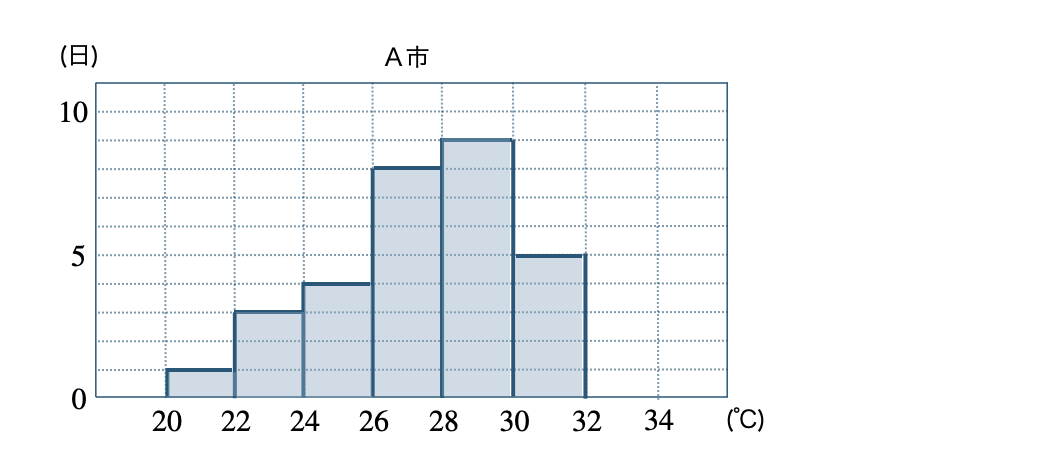
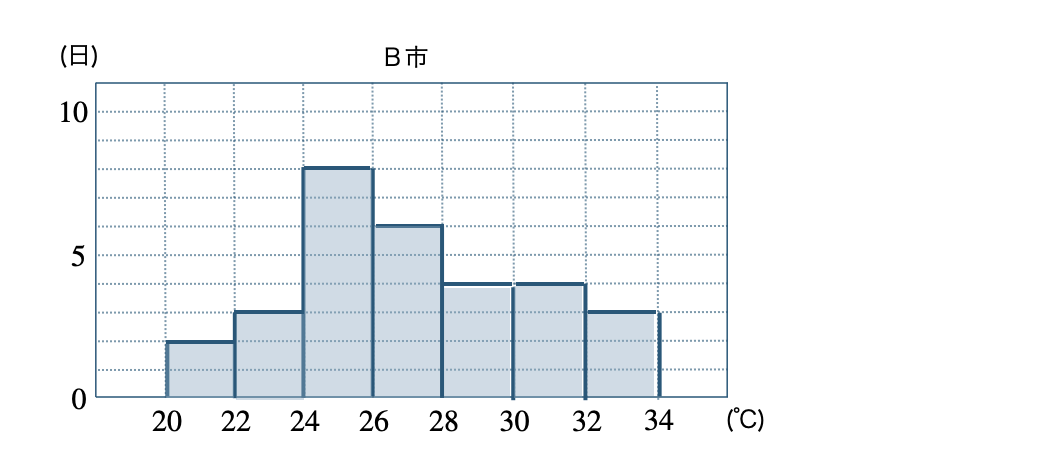
\({\small (3)}~\)
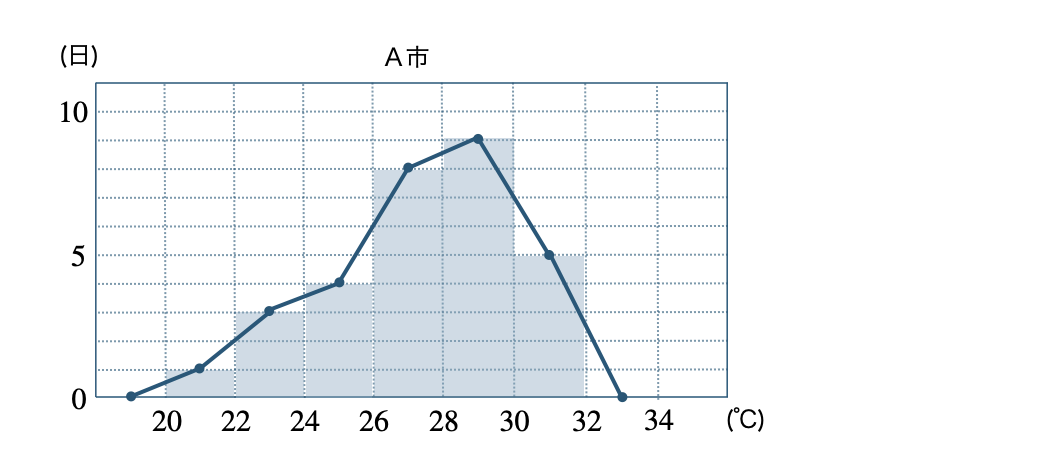
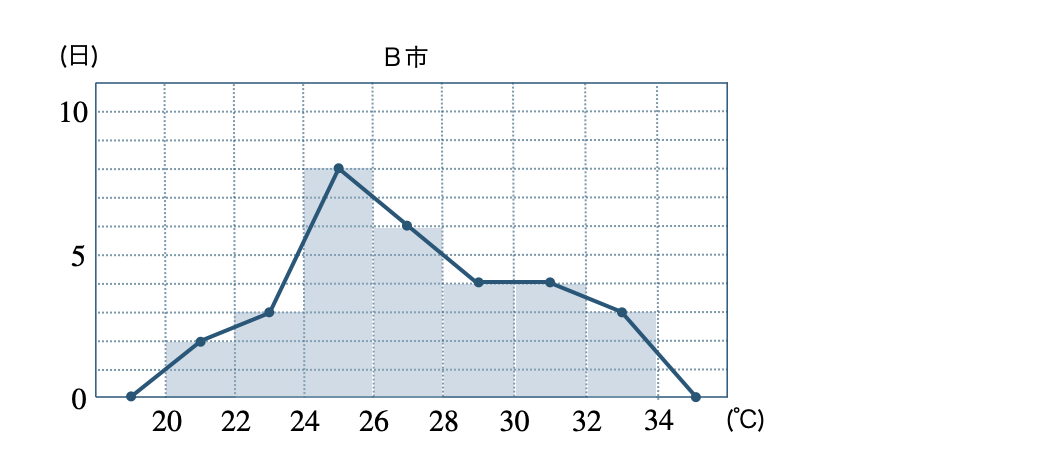

度数分布表と代表値
次の表は、\(20\) 人のグループAと \(23\) 人のグループBのあるゲームの得点の度数分布表である。次の問いに答えよ。
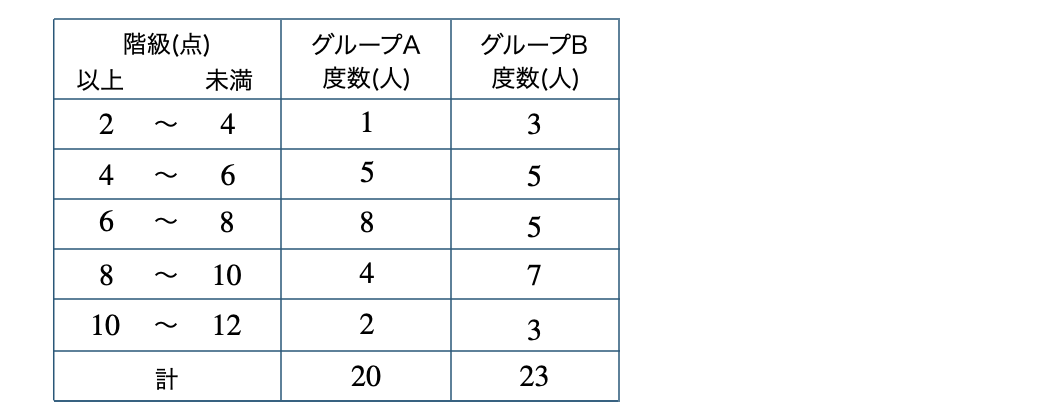
\({\small (1)}~\)それぞれのグループの最頻値を求めよ。
\({\small (2)}~\)それぞれのグループの中央値を求めよ。
\({\small (3)}~\)それぞれのグループの平均値を求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
Aの最頻値は \(7\) 点
Bの最頻値は \(9\) 点
\({\small (2)}~\)
Aの中央値は \(7\) 点
Bの中央値は \(7\) 点
\({\small (3)}~\)
Aの平均値は \(7.1\) 点
Bの平均値は約 \(7.2\) 点

相対度数と累積相対度数
次の表は、\(20\) 人のグループAと \(23\) 人のグループBのあるゲームの得点の度数分布表である。次の問いに答えよ。
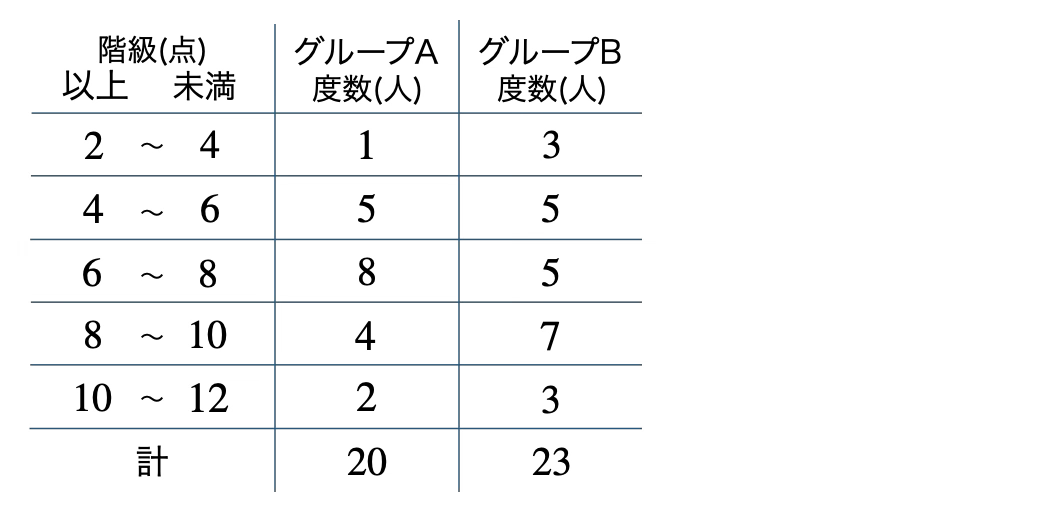
\({\small (1)}~\)それぞれのグループの相対度数、累積度数、累積相対度数の表を完成させよ。
\({\small (2)}~\)以下の問いに答えよ。
① それぞれのグループの最頻値をとる階級の人数は全体の何%か求めよ。
② それぞれのグループの得点が \(10\) 点未満の割合を求めよ。
③ それぞれのグループの得点が \(6\) 点以上の割合がを求めよ。
\({\small (3)}~\)それぞれのグループの相対度数のヒストグラムと度数折れ線グラフをかけ。
\({\small (4)}~\)それぞれのグループの累積相対度数のヒストグラムと累積相対度数の折れ線グラフをかけ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
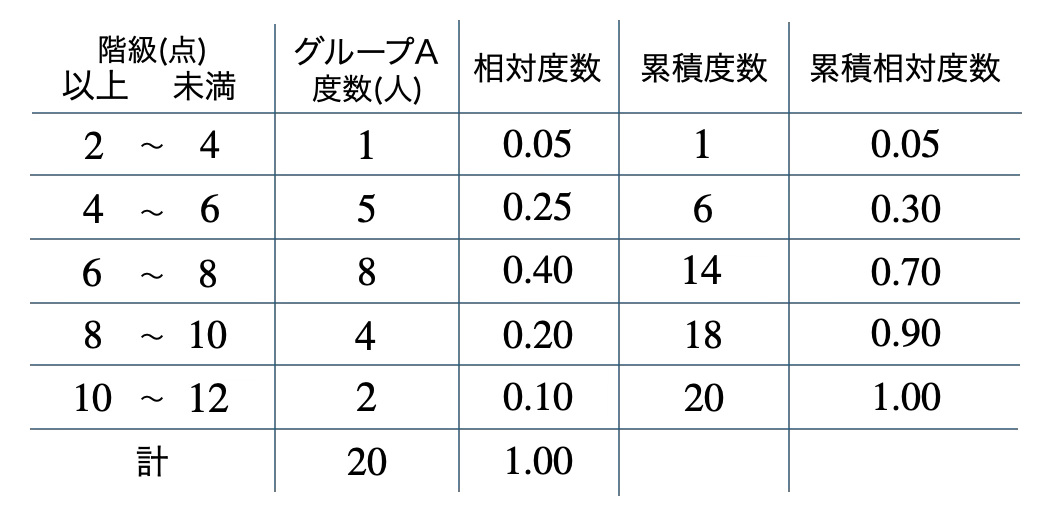
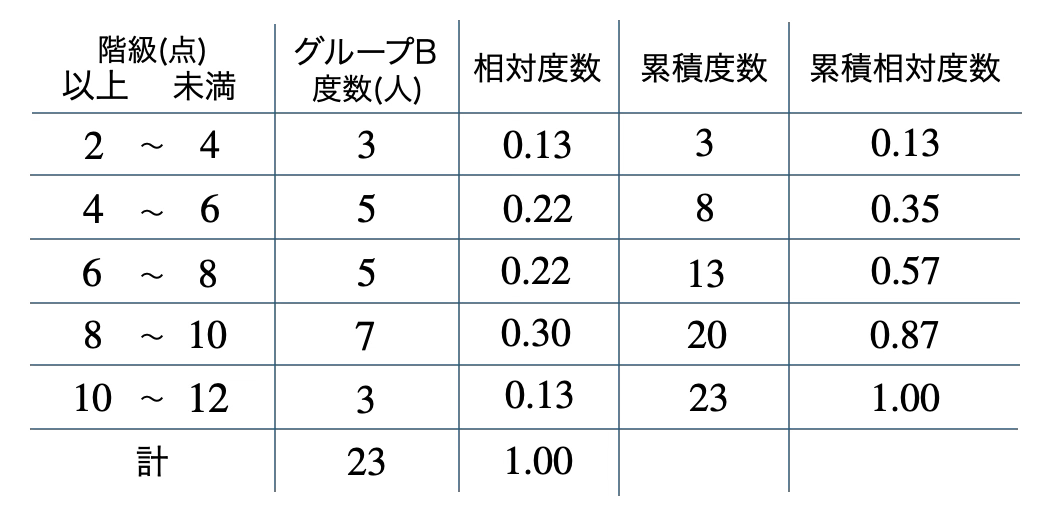
\({\small (2)}~\)
\(~~{\large ①}~\)
グループA \(40\) %、グループB \(30\) %
\(~~{\large ②}~\)
グループA \(0.90\)、グループB \(0.87\)
\(~~{\large ③}~\)
グループA \(0.70\)、グループB \(0.63\)
\({\small (3)}~\)
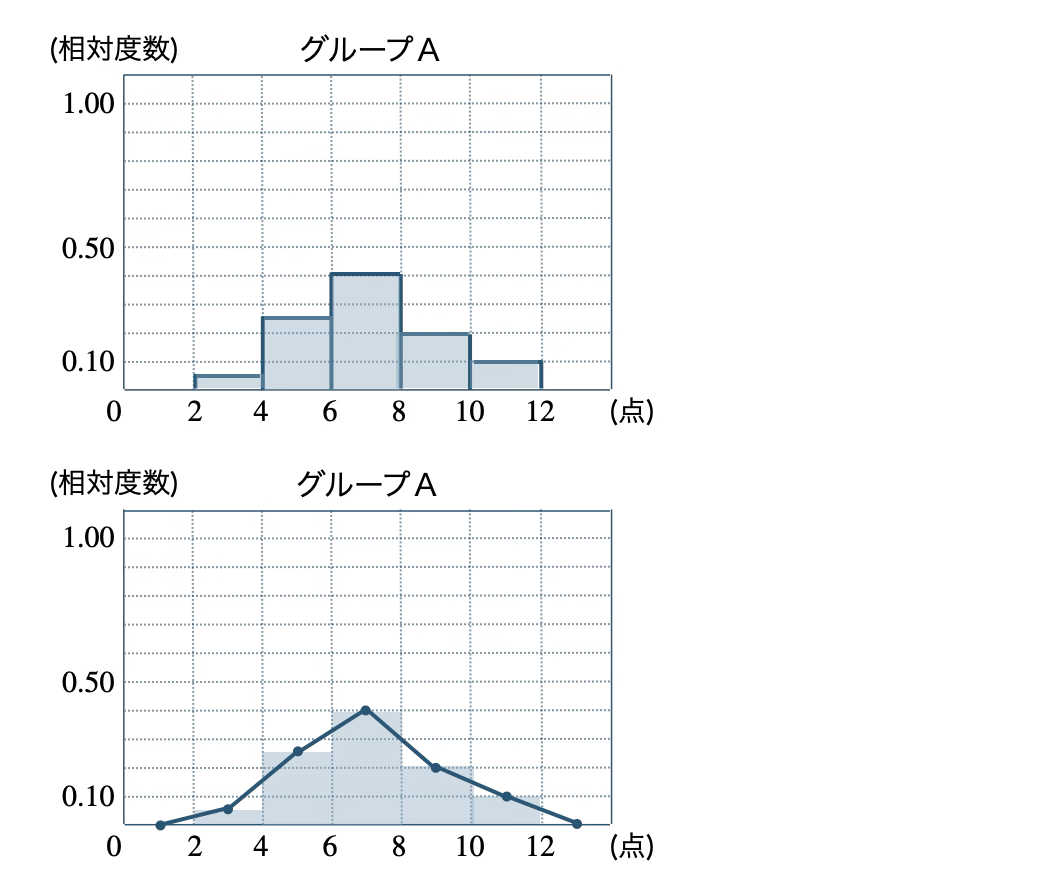
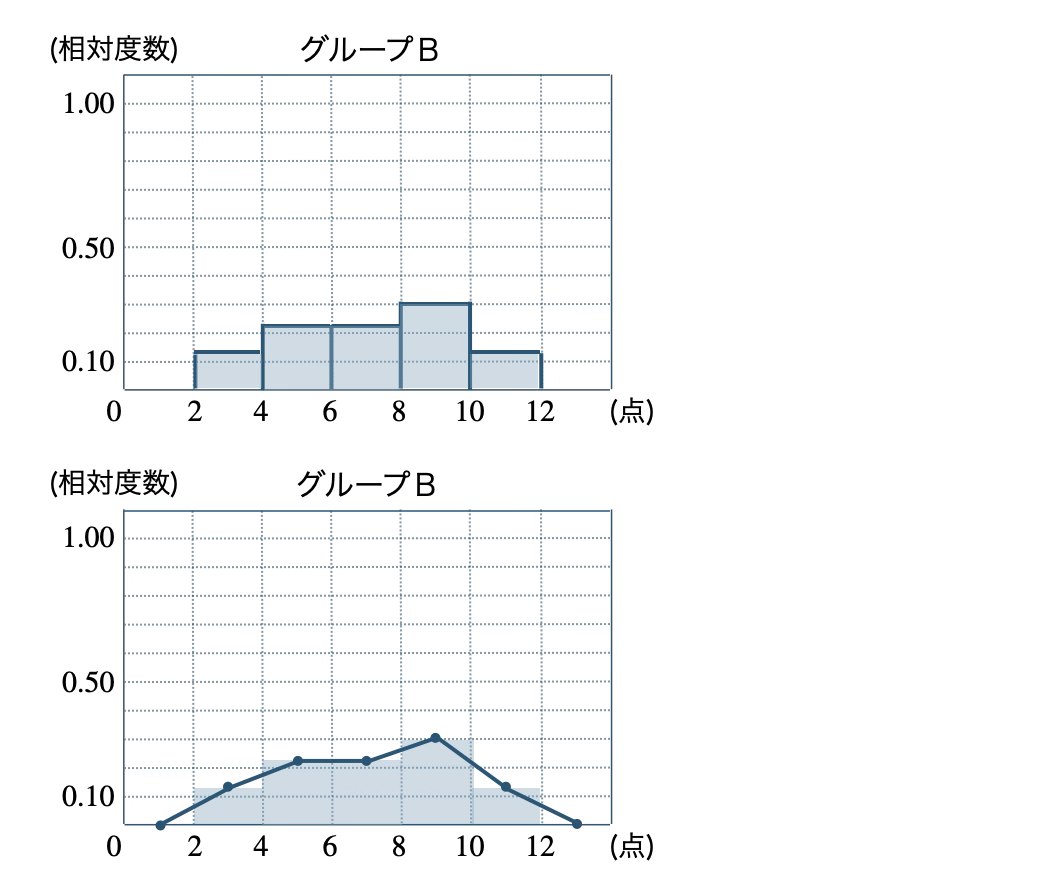
\({\small (4)}~\)
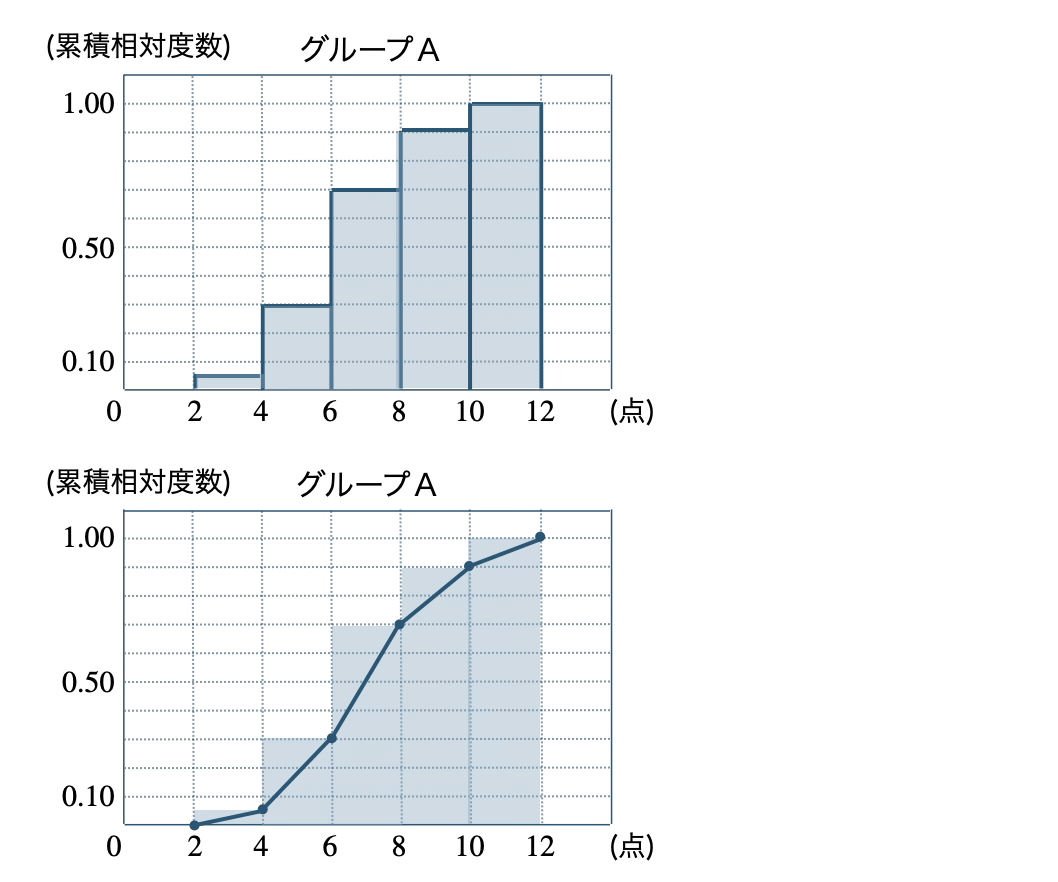
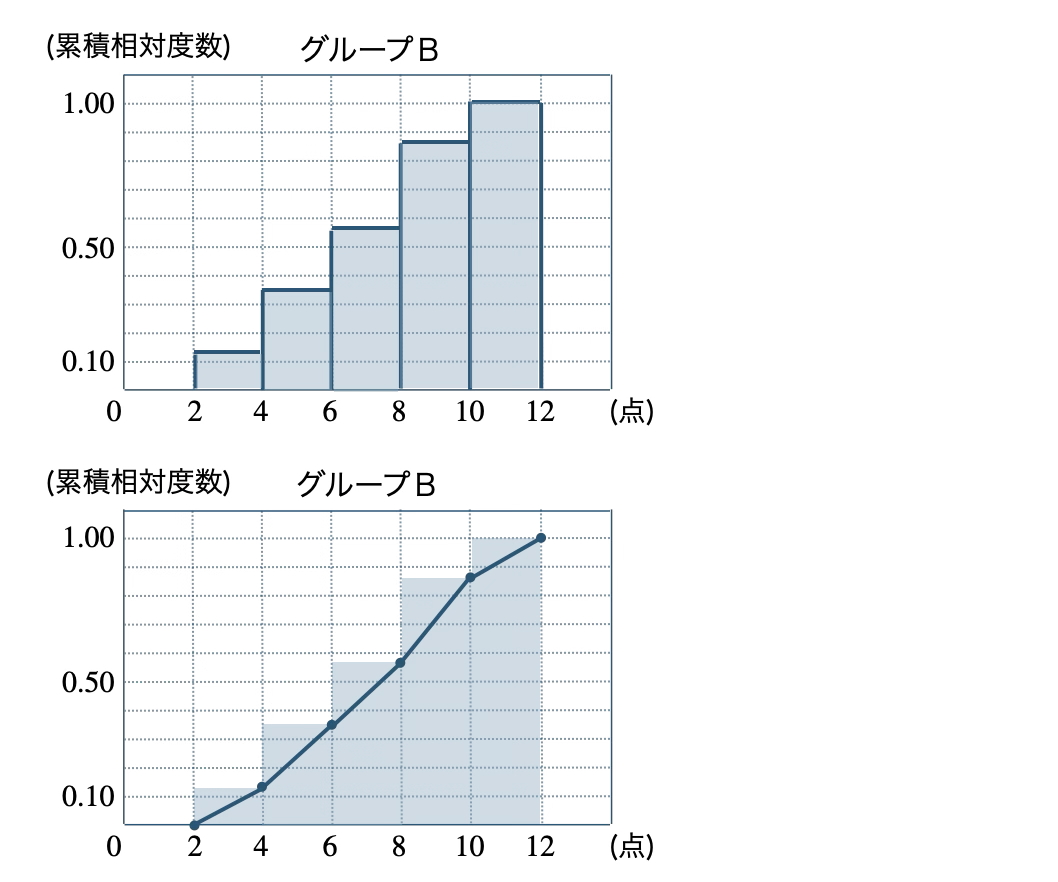

起こりやすさと確率
次の表は、ペットボトルのふたを投げたとき、表が出た回数をまとめた表である。

次の問いに答えよ。
\({\small (1)}~\) \(500\) 回投げたときの相対度数を求めよ。
\({\small (2)}~\)回数をかさねると、表が出る相対度数はどんな値に近づくか答えよ。
\({\small (3)}~\)表と表以外ではどちらが出やすいといえるか答えよ。
\({\small (4)}~\) \(8000\) 回投げたとき、表は何回出ると考えられるか答えよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)\(0.43\)
\({\small (2)}~\)\(0.42\)
\({\small (3)}~\)表以外のほうが出やすい
\({\small (4)}~\)\(3368\) 回



