このページは「中学数学2 1次関数」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう!
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
【問題一覧】中学数学2 1次関数
1次関数の式
次の問いに答えよ。
\({\small (1)}~\)深さ \(30~{\rm cm}\) の水そうに高さ \(10~{\rm cm}\) まで水が入っている。\(1\) 分間で \(2~{\rm cm}\) の割合で水面が高くなるように水を入れた。水を入れ始めてから \(x\) 分後の水面の高さを \(y~{\rm cm}\) とする。
| \(x\) 分 | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(y\) m | \(10\) | ① | ② | ③ | ④ | ⑤ | ⑥ |
①〜⑥に入る数を答えよ。また、\(y\) を \(x\) の式で表せ。
\({\small (2)}~\)次の \(x\) と \(y\) について、\(y\) を \(x\) の式で表して \(y\) が \(x\) の1次関数であるものを選べ。
① \(1\) 個 \(120\) 円のりんご \(x\) 個の
合計代金が \(y\) 円である。
② 底辺 \(x~{\rm cm}\)、高さ \(y~{\rm cm}\) の三角形の
面積が \(15~{\rm cm}^2\) である。
③ \(18~{\rm cm}\) の線香に火をつけると、\(1\) 分間に
\(1~{\rm cm}\) ずつ短くなるとき、\(x\) 分後の線香の
長さが \(y~{\rm cm}\) である。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(12\) ② \(14\) ③ \(16\) ④ \(18\) ⑤ \(20\) ⑥ \(22\)
\(y=2x+10\)
\({\small (2)}~\)
① \(\begin{split}y=120x\end{split}\)、\(y\) は \(x\) の1次関数となる
② \(\begin{split}y=\frac{\,30\,}{\,x\,}\end{split}\)、\(y\) は \(x\) に反比例する
③ \(\begin{split}y=-x+18\end{split}\)、\(y\) は \(x\) の1次関数となる

1次関数の変化の割合
次の問いに答えよ。
\({\small (1)}~\)次の関数の \(x\) の値が \(-2\) から \(3\) まで増加するとき、\(x\) の増加量、\(y\) の増加量、変化の割合をそれぞれ答えよ。
① \(\begin{split}y=2x-1\end{split}\)
② \(\begin{split}y=-3x+6\end{split}\)
③ \(\begin{split}y=4x\end{split}\)
④ \(\begin{split}y=\frac{\,12\,}{\,x\,}\end{split}\)
\({\small (2)}~\)次の1次関数の変化の割合を答えよ。また、\(x\) の増加量が \(2\) のとき、\(y\) の増加量を求めよ。
① \(\begin{split}y=6x-5\end{split}\)
② \(\begin{split}y=-5x+1\end{split}\)
③ \(\begin{split}y=\frac{\,2\,}{\,3\,}x+2\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(x\) の増加量 \(5\)、\(y\) の増加量 \(10\)、変化の割合 \(2\)
② \(x\) の増加量 \(5\)、\(y\) の増加量 \(-15\)、変化の割合 \(-3\)
③ \(x\) の増加量 \(5\)、\(y\) の増加量 \(20\)、変化の割合 \(4\)
④ \(x\) の増加量 \(5\)、\(y\) の増加量 \(10\)、変化の割合 \(2\)
\({\small (2)}~\)
① 変化の割合 \(6\)、\(y\) の増加量 \(12\)
② 変化の割合 \(-5\)、\(y\) の増加量 \(-10\)
③ 変化の割合 \(\begin{split}{\frac{\,2\,}{\,3\,}}\end{split}\)、\(y\) の増加量 \(\begin{split}{\frac{\,4\,}{\,3\,}}\end{split}\)

1次関数のグラフと切片
次の問いに答えよ。
\({\small (1)}~\)次の1次関数のグラフは \(y=2x\) のグラフをどのように平行移動したものか答えよ。また、1次関数のグラフをかけ。
① \(\begin{split}y=2x+3\end{split}\)
② \(\begin{split}y=2x-1\end{split}\)
\({\small (2)}~\)次の直線の \(y\) 軸と交わる座標と切片を求めよ。
① \(\begin{split}y=3x+5\end{split}\)
② \(\begin{split}y=-\frac{\,1\,}{\,3\,}x-\frac{\,3\,}{\,2\,}\end{split}\)
③ \(\begin{split}y=2x\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(y\) 軸方向に \(3\) だけ平行移動
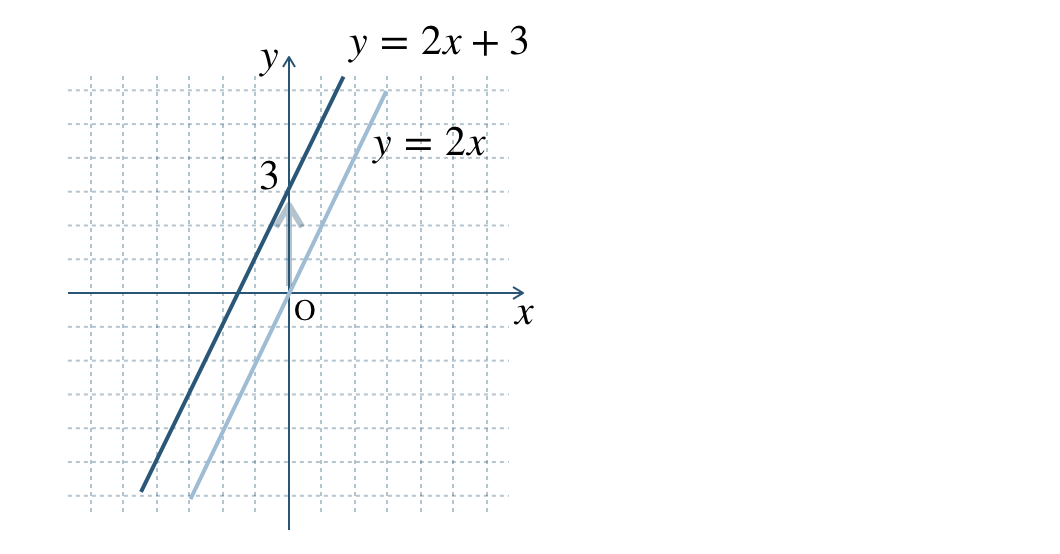
② \(y\) 軸方向に \(-1\) だけ平行移動
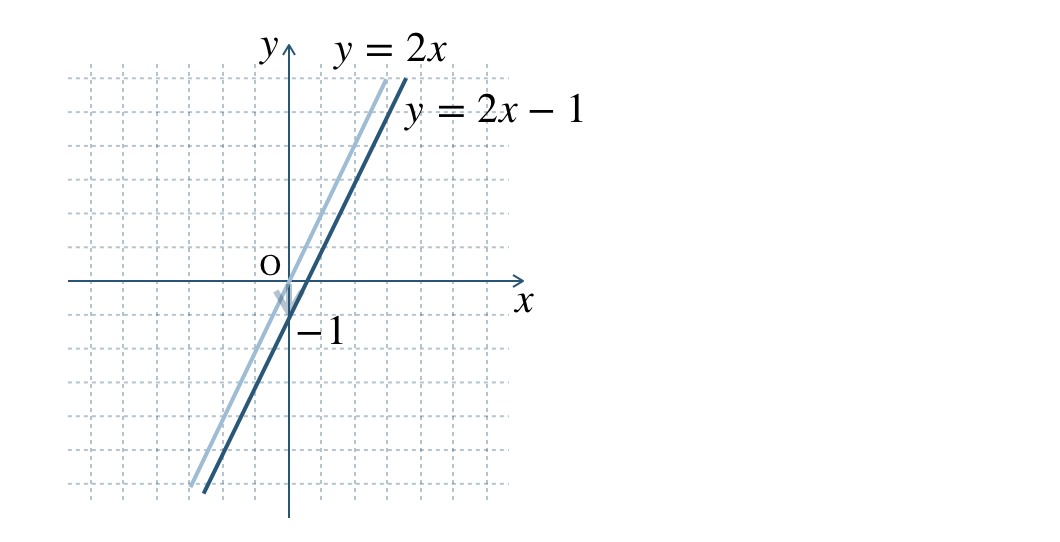
\({\small (2)}~\)
① 交点は \((0~,~5)\)、切片は \(5\)
② 交点は \(\begin{split}\left(0~,~-{\frac{\,3\,}{\,2\,}}\right)\end{split}\)、切片は \(\begin{split}-{\frac{\,3\,}{\,2\,}}\end{split}\)
③ 交点は \((0~,~0)\)、切片は \(0\)

1次関数のグラフと傾き
次の問いに答えよ。
\({\small (1)}~\)次の直線において、右に \(1\) 進むとき、右に \(3\) 進むときはそれぞれ上に(または下に)どれだけ進むか答えよ。
① \(\begin{split}y=x+3\end{split}\)
② \(\begin{split}y=-2x+1\end{split}\)
③ \(\begin{split}y=3x-5\end{split}\)
\({\small (2)}~\)次の直線の傾きを答えよ。また、右上がりか右下がりか答えよ。
① \(\begin{split}y=-5x+1\end{split}\)
② \(\begin{split}y=\frac{\,3\,}{\,4\,}x+\frac{\,1\,}{\,2\,}\end{split}\)
③ \(\begin{split}y=-x\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)
①
右に \(1\) 進むとき、上に \(1\) 進む
右に \(3\) 進むとき、上に \(3\) 進む
②
右に \(1\) 進むとき、下に \(2\) 進む
右に \(3\) 進むとき、下に \(6\) 進む
③
右に \(1\) 進むとき、上に \(3\) 進む
右に \(3\) 進むとき、上に \(9\) 進む
\({\small (2)}~\)
① 傾き \(-5\)、右下がり
② 傾き \(\begin{split}{\frac{\,3\,}{\,4\,}}\end{split}\)、右上がり
③ 傾き \(-1\)、右下がり

1次関数のグラフのかき方
次の1次関数のグラフをかけ。
\(\begin{split}{\small (1)}~y=x-3\end{split}\)
\(\begin{split}{\small (2)}~y=-2x+4\end{split}\)
\(\begin{split}{\small (3)}~y=\frac{\,1\,}{\,2\,}x-1\end{split}\)
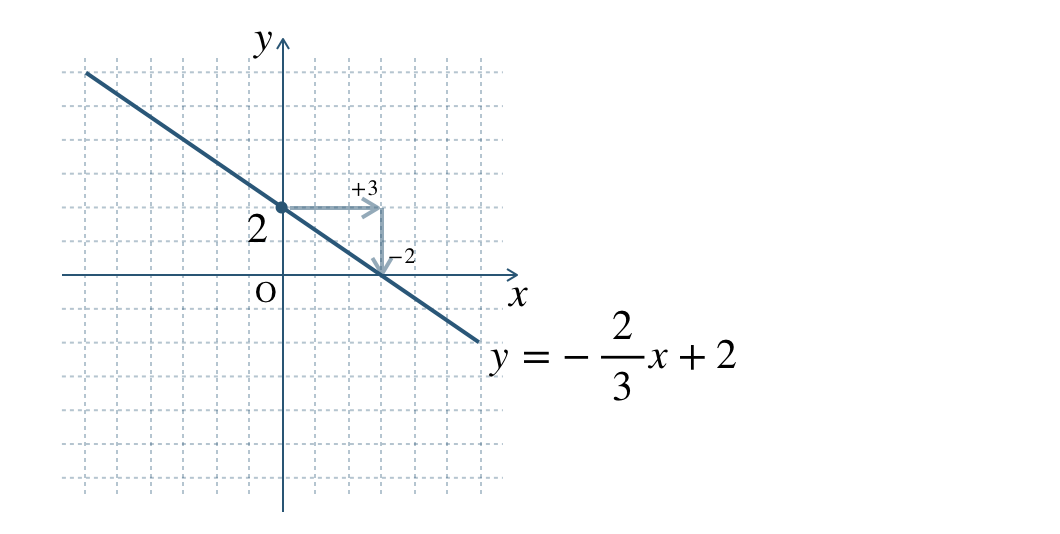
\(\begin{split}{\small (4)}~y=-\frac{\,2\,}{\,3\,}x+2\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)
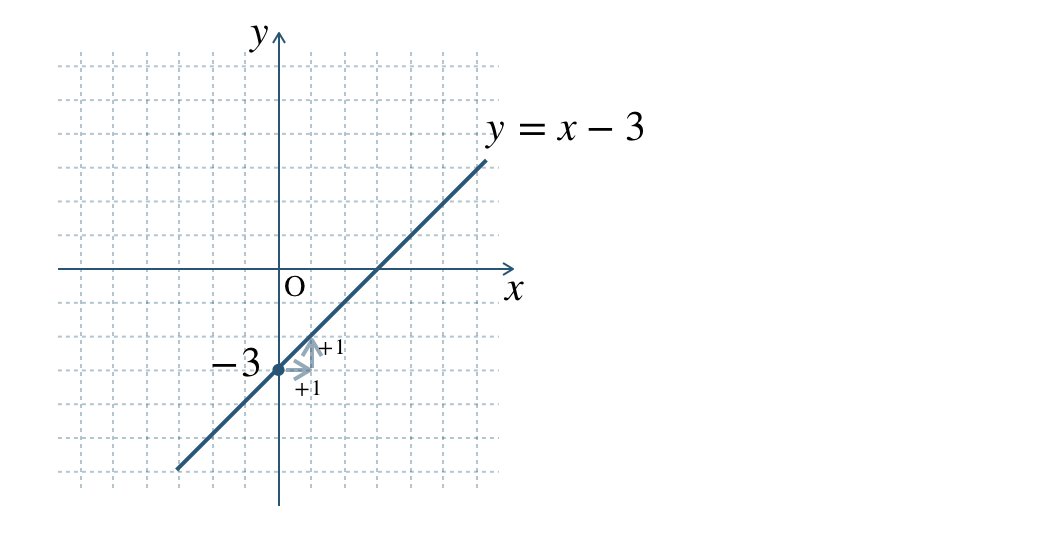
\({\small (2)}~\)
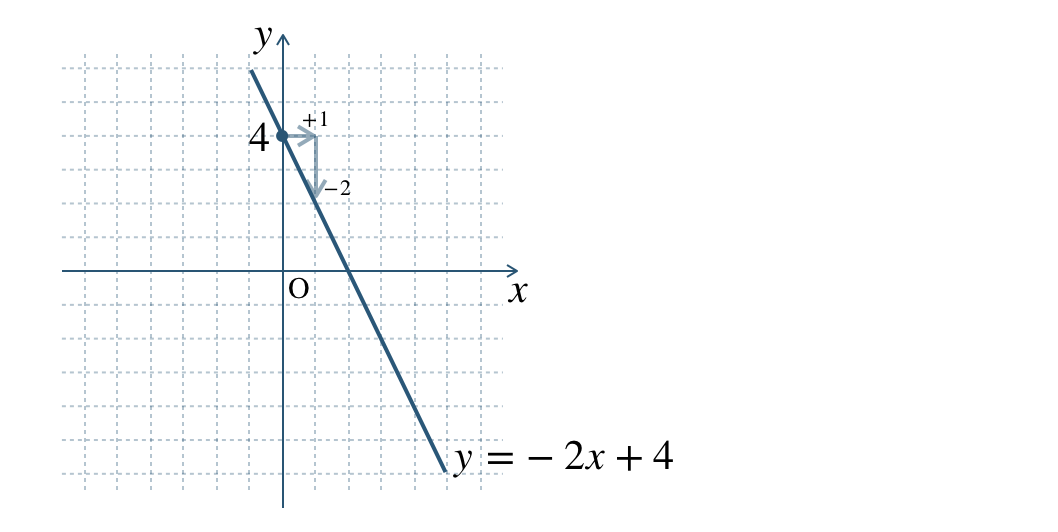
\({\small (3)}~\)
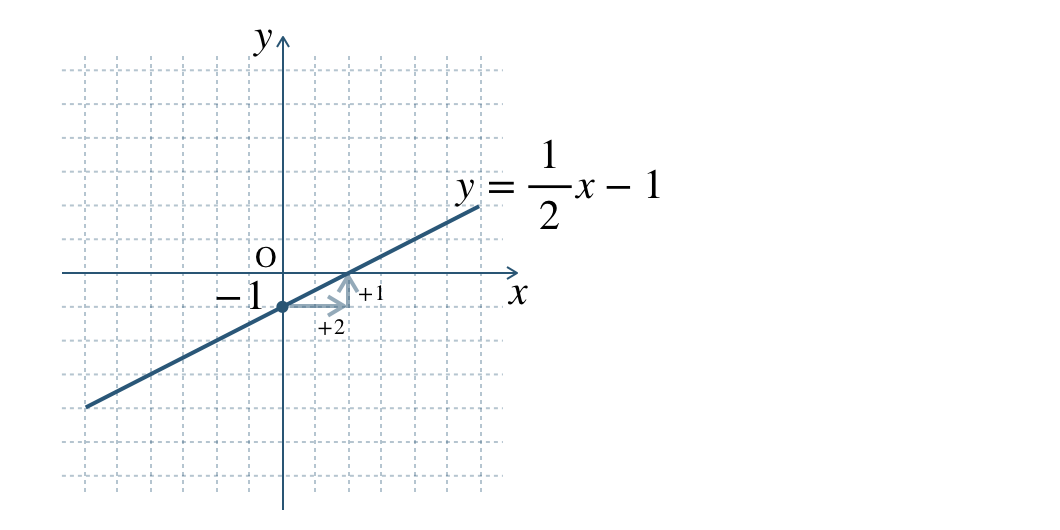
\({\small (4)}~\)

1次関数のグラフの変域
\(x\) の変域が決められた、次の1次関数のグラフをかき、\(y\) の変域を求めよ。
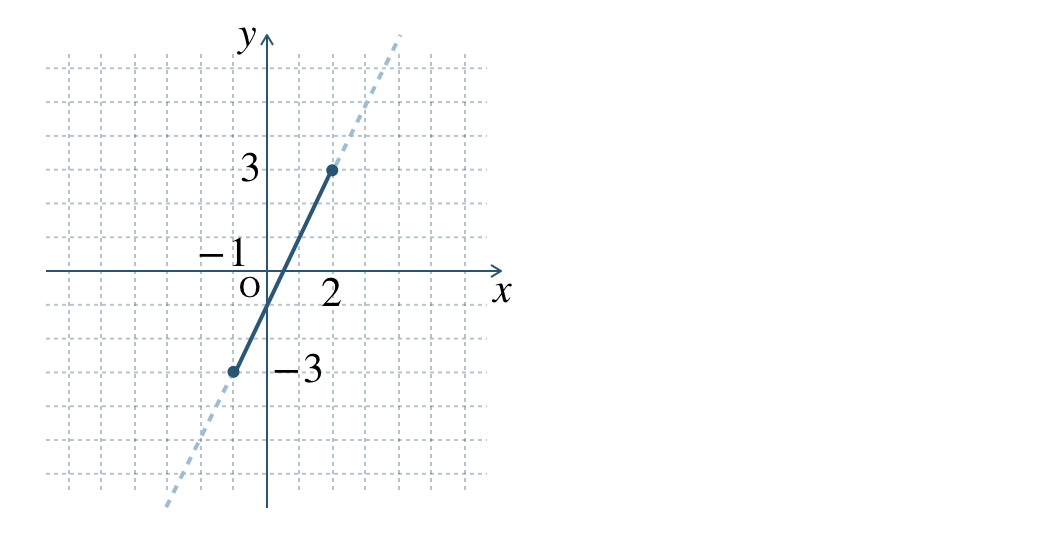
\(\begin{split}{\small (1)}~y=2x-1~~(-1≦x≦2)\end{split}\)
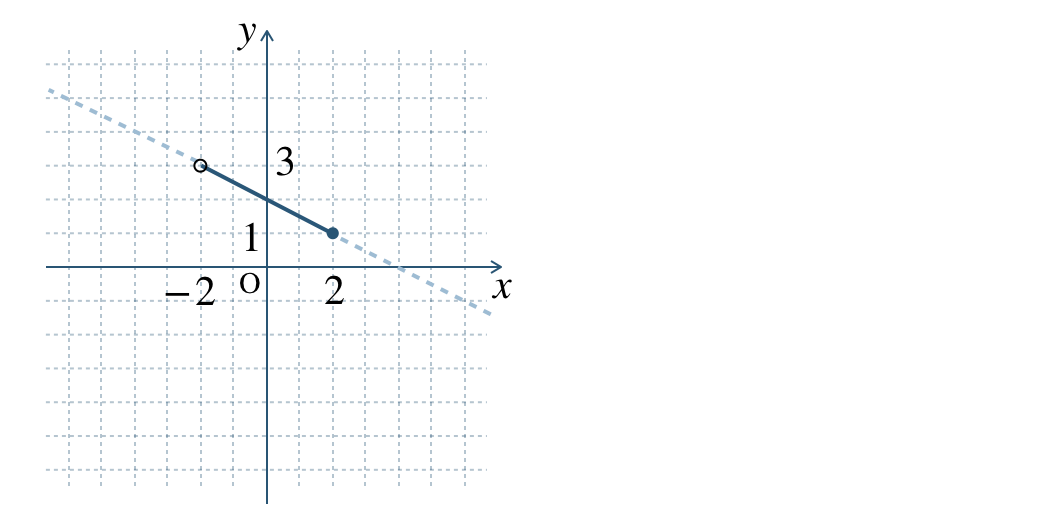
\(\begin{split}{\small (2)}~y=-\frac{\,1\,}{\,2\,}x+2~~(-2<x≦2)\end{split}\)
\(\begin{split}{\small (3)}~y=\frac{\,2\,}{\,3\,}x-2~~(x>0)\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~-3≦y≦3\)
\({\small (2)}~1≦y<3\)
\({\small (3)}~y>-2\)

グラフから1次関数の式を求める
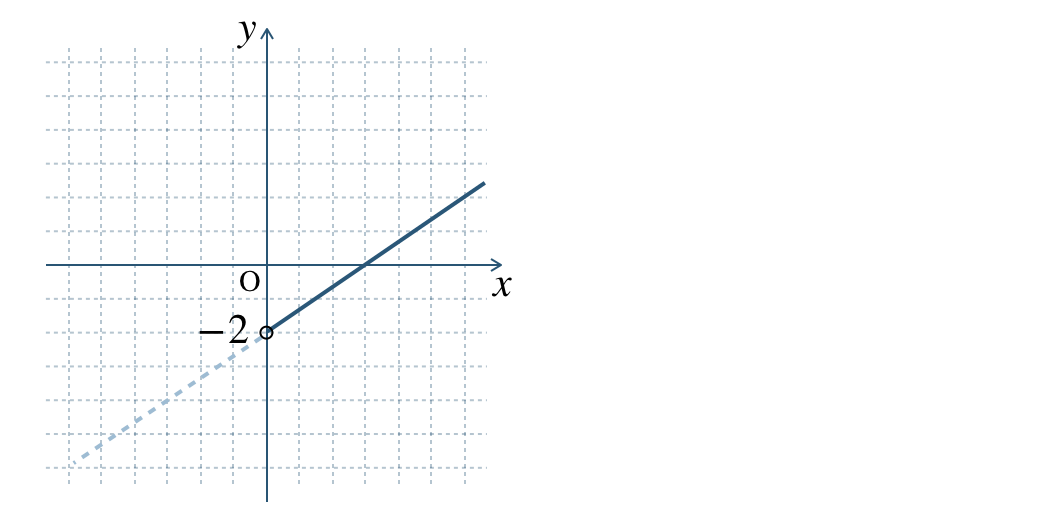
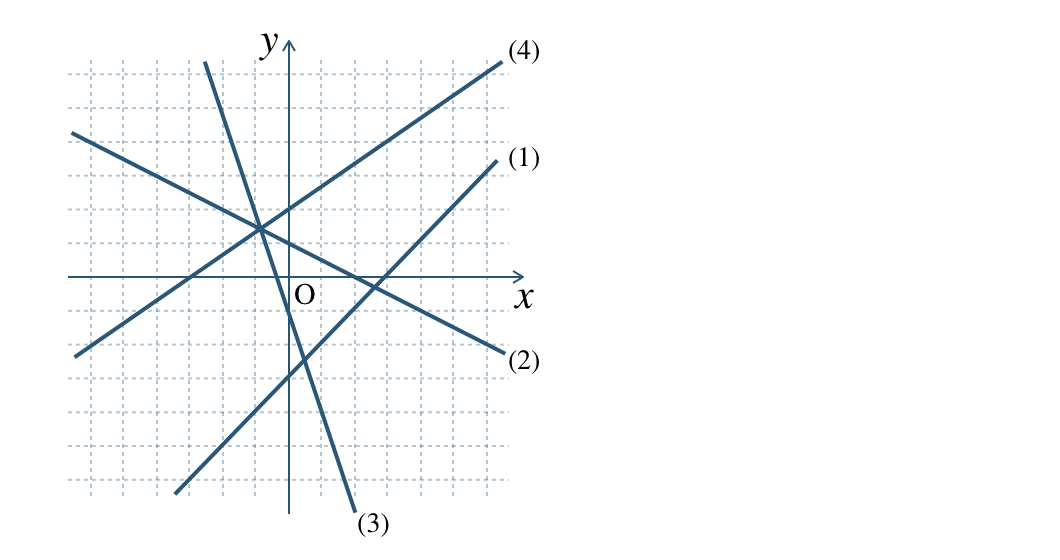
次の図の (1) 〜 (4) の直線の式を求めよ。
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~y=x-3\end{split}\)
\(\begin{split}{\small (2)}~y=-\frac{\,1\,}{\,2\,}x+1\end{split}\)
\(\begin{split}{\small (3)}~y=-3x-1\end{split}\)
\(\begin{split}{\small (4)}~y=\frac{\,2\,}{\,3\,}x+2\end{split}\)

1次関数の式と条件
次の条件を満たす1次関数の式を求めよ。
\({\small (1)}~\)傾き \(2\)、切片 \(-3\)。
\({\small (2)}~\)傾き \(-1\)、点 \((1~,~4)\) を通る。
\({\small (3)}~\)変化の割合が \(\begin{split}{\frac{\,2\,}{\,3\,}}\end{split}\) であり、\(x=-3\) のとき \(y=1\)。
\({\small (4)}~\)グラフが \(\begin{split}y=-{\frac{\,1\,}{\,2\,}}x+3\end{split}\) に平行であり、点 \((-6~,~1)\) を通る。
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~y=2x-3\end{split}\)
\(\begin{split}{\small (2)}~y=-x+5\end{split}\)
\(\begin{split}{\small (3)}~y=\frac{\,2\,}{\,3\,}x+3\end{split}\)
\(\begin{split}{\small (4)}~y=-\frac{\,1\,}{\,2\,}x-2\end{split}\)

2点を通る直線の式
次の直線の式を求めよ。
\({\small (1)}~\)2点 \((1~,~2)~,~(2~,~5)\) を通る。
\({\small (2)}~\)\(x=2\) のとき \(y=2\)、\(x=-4\) のとき \(y=5\) となる。
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~y=3x-1\end{split}\)
\(\begin{split}{\small (2)}~y=-\frac{\,1\,}{\,2\,}x+3\end{split}\)

2元1次方程式のグラフ
次の方程式のグラフをかけ。
\(\begin{split}{\small (1)}~~3x+2y-6=0\end{split}\)
\(\begin{split}{\small (2)}~~\frac{\,1\,}{\,6\,}x-\frac{\,1\,}{\,3\,}y=1\end{split}\)
\(\begin{split}{\small (3)}~~3x=6\end{split}\)
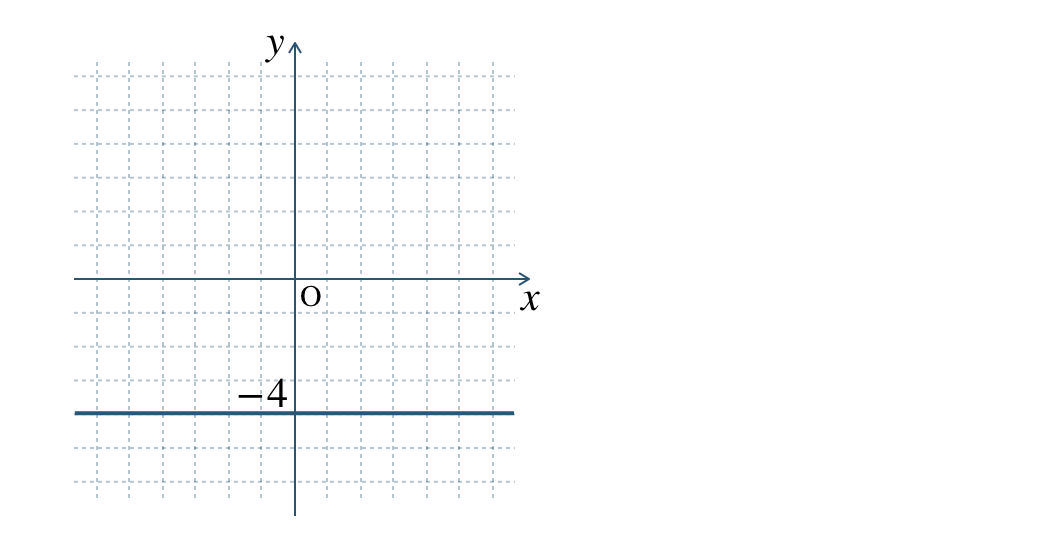
\(\begin{split}{\small (4)}~~3y+12=0\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)
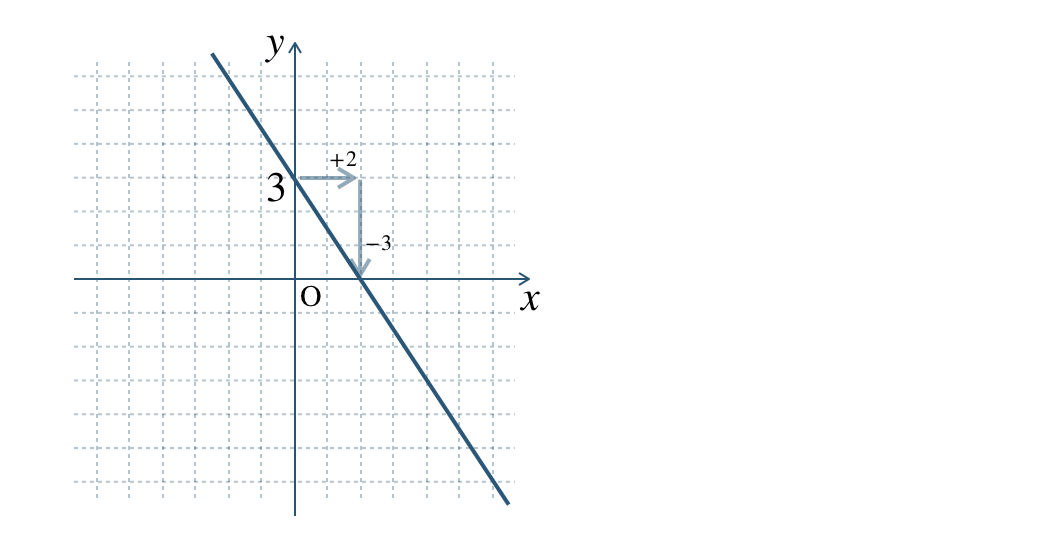
\({\small (2)}~\)
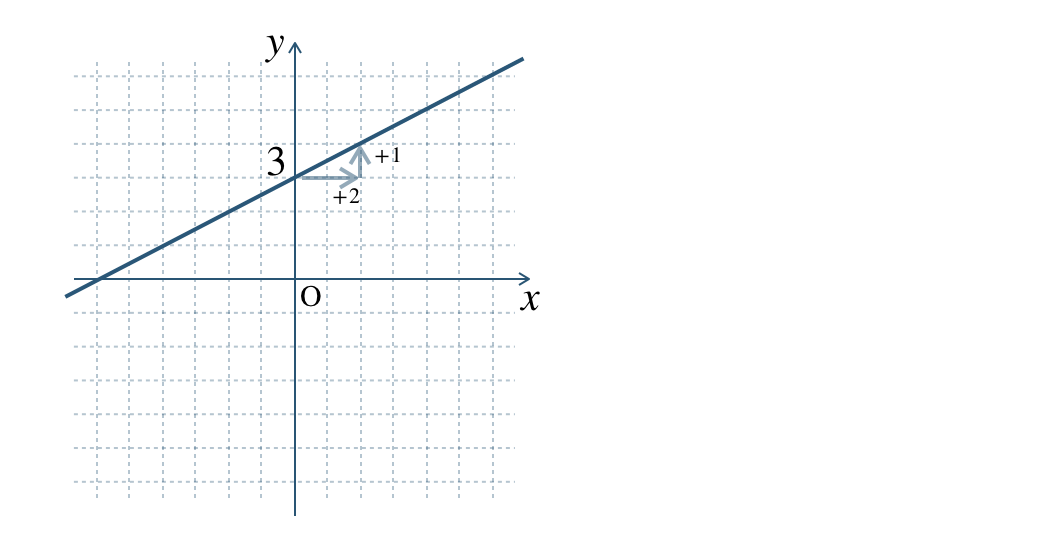
\({\small (3)}~\)
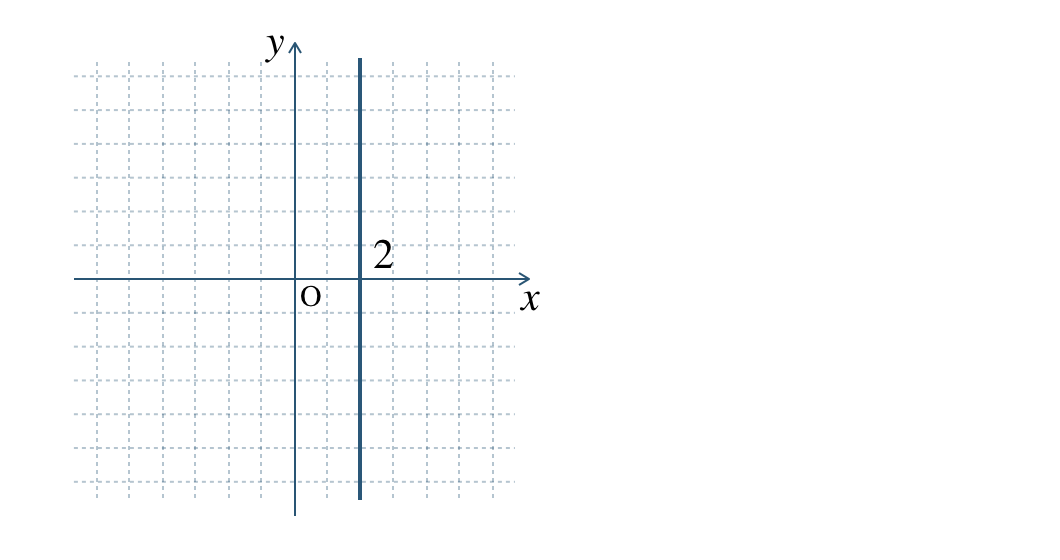
\({\small (4)}~\)

連立方程式とグラフ
次の問いに答えよ。
\({\small (1)}~\)次の連立方程式の解をグラフをかくことで求めよ。
① \(\begin{eqnarray} \left\{\begin{array}{l}x-y=1 \\2x+3y=12 \end{array}\right.\end{eqnarray}\)
② \(\begin{eqnarray} \left\{\begin{array}{l}2x+y+3=0 \\x-2y+4=0 \end{array}\right.\end{eqnarray}\)
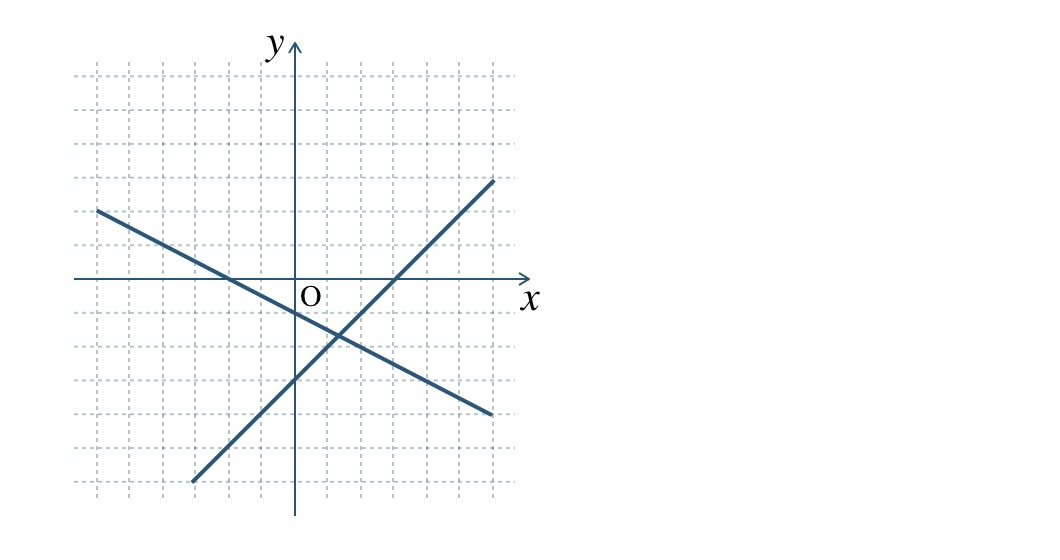
\({\small (2)}~\)次の図の2直線の交点の座標を求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(\begin{split}x=3~,~y=2\end{split}\)
② \(\begin{split}x=-2~,~y=1\end{split}\)
\(\begin{split}{\small (2)}~\left(\frac{\,4\,}{\,3\,}~,~-\frac{\,5\,}{\,3\,}\right)\end{split}\)

1次関数と道のり
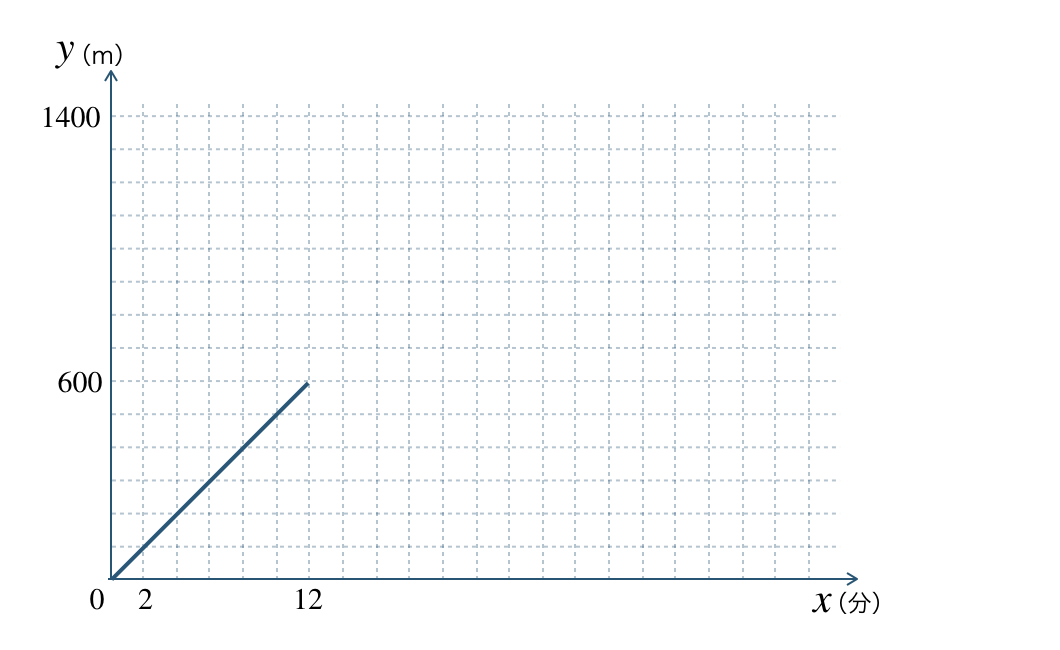
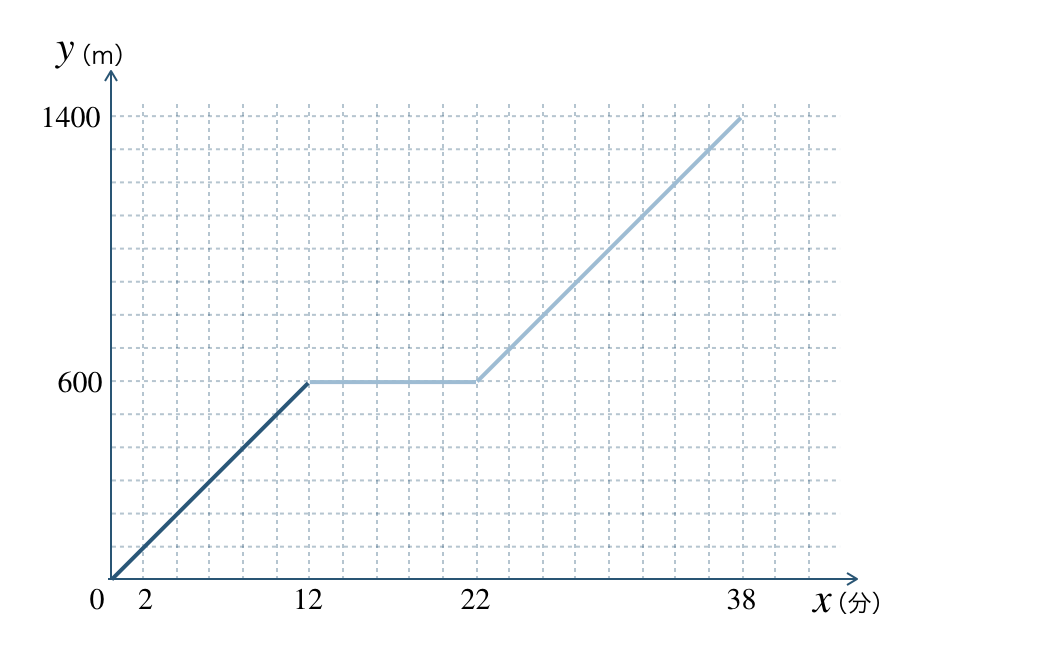
Aさんは家から学校までの道のり \(1400~{\rm m}\) を7時ちょうどに出発して歩いた。
次のグラフは、家を出発して \(x\) 分後の家からの道のりを \(y~{\rm m}\) として、\(x\) と \(y\) の関係を表したものである。
\({\small (1)}~\)Aさんは分速何 \({\rm m}\) で歩いたか答えよ。
\({\small (2)}~\)Aさんは家から \(600~{\rm m}\) の地点で \(10\) 分間休んだ後、学校まで同じ速さで歩いた。このことをグラフて表せ。
\({\small (3)}~\)Aさんが休んだ後、学校まで歩いた関係を \(y\) を \(x\) の式て表せ。
\({\small (4)}~\)Bさんは7時22分に家から学校まで分速 \(140~{\rm m}\) で走った。Bさんが家から学校まで走る \(x\) と \(y\) の関係をグラフで表し、\(y\) を \(x\) の式で表せ。
\({\small (5)}~\)BさんがAさんに追いつくのは7時何分何秒の家から何 \({\rm m}\) の地点か答えよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)分速 \(50~{\rm m}\)
\({\small (2)}~\)
\({\small (3)}~y=50x-500\)
\({\small (4)}~y=140x-3080\)
\({\small (5)}~\)7時28分40秒、家から \(\begin{split}{\frac{\,2800\,}{\,3\,}}~{\rm m}\end{split}\) の地点

1次関数と動く点
点 \({\rm P}\) は \(1\) 秒間に \(2~{\rm cm}\) で点 \({\rm B}\) →点 \({\rm A}\) →点 \({\rm D}\) →点 \({\rm C}\) と動く。\(x\) 秒後の \(\triangle {\rm PBC}\) の面積を \(y~{\rm cm}^2\) とするとき、次の問いに答えよ。
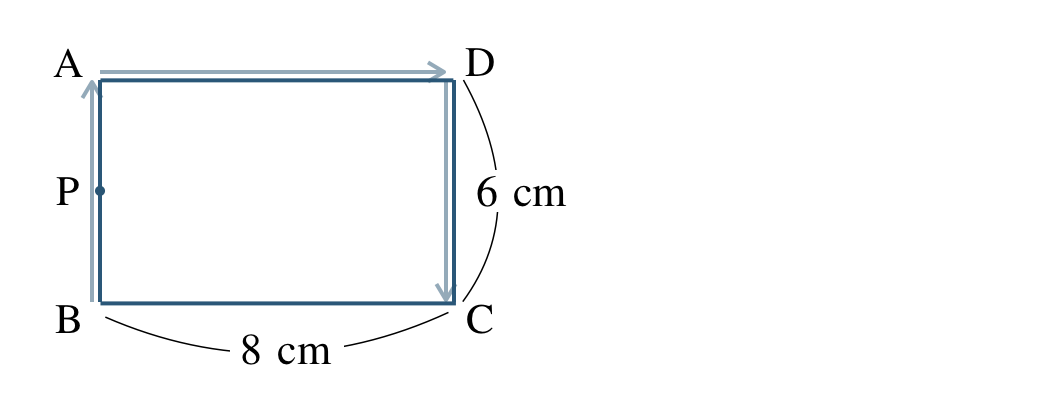
\({\small (1)}~\)点 \({\rm P}\) が辺 \({\rm AB}\) 上にあるとき、\(x\) の変域と \(y\) を \(x\) の式で表せ。
\({\small (2)}~\)点 \({\rm P}\) が辺 \({\rm AD}\) 上にあるとき、\(x\) の変域と \(y\) を \(x\) の式で表せ。
\({\small (3)}~\)点 \({\rm P}\) が辺 \({\rm CD}\) 上にあるとき、\(x\) の変域と \(y\) を \(x\) の式で表せ。
\({\small (4)}~\)点 \({\rm P}\) が点 \({\rm B}\) から点 \({\rm C}\) まで動くときの \(y\) と \(x\) の関係をグラフで表せ。
\({\small (5)}~\)\(\triangle {\rm PBC}\) の面積が \(16~{\rm cm}^2\) となるとき、点 \({\rm P}\) が点 \({\rm B}\) を出発して何秒後か答えよ。
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~y=8x~~,~~0≦x≦3\end{split}\)
\(\begin{split}{\small (2)}~y=24~~,~~3≦x≦7\end{split}\)
\(\begin{split}{\small (3)}~y=-8x+80~~,~~7≦x≦10\end{split}\)
\(\begin{split}{\small (4)}~\end{split}\)
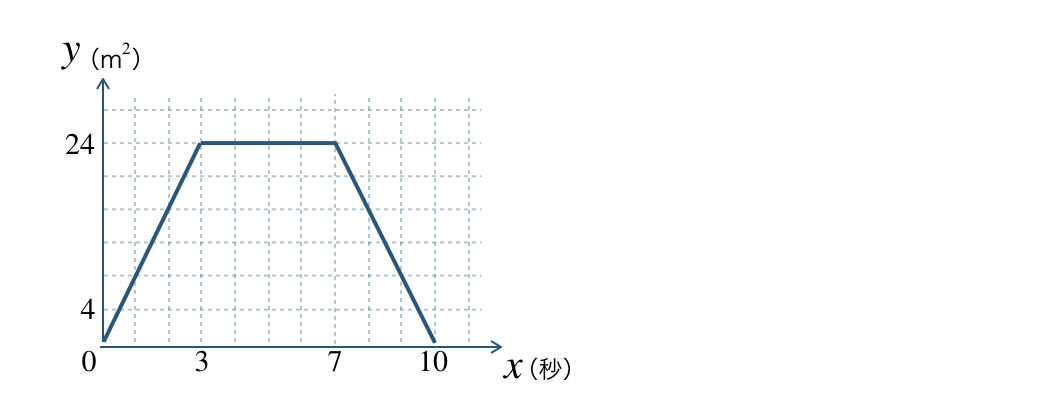
\(\begin{split}{\small (5)}~\end{split}\)2秒後と8秒後



