このページは「中学数学3 展開と因数分解」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう!
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
【問題一覧】中学数学3 展開と因数分解
単項式と多項式の乗法・除法
次の計算をせよ。
\(\begin{split}{\small (1)}~~3a(x-2y)\end{split}\)
\(\begin{split}{\small (2)}~~(2a-3b){\, \small \times \,}(-2a)\end{split}\)
\(\begin{split}{\small (3)}~~3x(2x-3y+z)\end{split}\)
\(\begin{split}{\small (4)}~~a(2a-1)+3a(a+4)\end{split}\)
\(\begin{split}{\small (5)}~~2x(x+5)-3x(x-1)\end{split}\)
\(\begin{split}{\small (6)}~~(9a^2-21ab){\, \small \div \,}(-3a)\end{split}\)
\(\begin{split}{\small (7)}~~(2x^2+3x){\, \small \div \,}\frac{\,x \,}{\,5 \,}\end{split}\)
\(\begin{split}{\small (8)}~~(4a^2b-10ab){\, \small \div \,}\left(-\frac{\,2 \,}{\,3 \,}ab\right)\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~3ax-6ay\)
\({\small (2)}~-4a^2+6ab\)
\({\small (3)}~6x^2-9xy+3xz\)
\({\small (4)}~5a^2+11a\)
\({\small (5)}~-x^2+13x\)
\({\small (6)}~-3a+7b\)
\({\small (7)}~10x+15\)
\({\small (8)}~-6a+15\)

多項式の乗法(式の展開)
次の式を展開せよ。
\(\begin{split}{\small (1)}~~(x-2)(y+3)\end{split}\)
\(\begin{split}{\small (2)}~~(a-1)(b-5)\end{split}\)
\(\begin{split}{\small (3)}~~(2a+1)(a-3)\end{split}\)
\(\begin{split}{\small (4)}~~(x-y)(3x-5y)\end{split}\)
\(\begin{split}{\small (5)}~~(x+1)(x-y+3)\end{split}\)
\(\begin{split}{\small (6)}~~(a-2b+4)(a-3)\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~xy+3x-2y-6\)
\({\small (2)}~ab-5a-b+5\)
\({\small (3)}~2a^2-5a-3\)
\({\small (4)}~3x^2-8xy+5y^2\)
\({\small (5)}~x^2-xy+4x-y+3\)
\({\small (6)}~a^2-2ab+a+6b-12\)

乗法公式(展開の公式)
次の式を展開せよ。
\(\begin{split}{\small (1)}~~(x-3)(x+5)\end{split}\)
\(\begin{split}{\small (2)}~~(a-2)(a-4)\end{split}\)
\(\begin{split}{\small (3)}~~(x+3)^2\end{split}\)
\(\begin{split}{\small (4)}~~(x-2)^2\end{split}\)
\(\begin{split}{\small (5)}~~(x+3)(x-3)\end{split}\)
\(\begin{split}{\small (6)}~~(5-a)(5+a)\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~x^2+2x-15\)
\({\small (2)}~a^2-6a+8\)
\({\small (3)}~x^2+6x+9\)
\({\small (4)}~a^2-4a+4\)
\({\small (5)}~x^2-9\)
\({\small (6)}~25-a^2\)

いろいろな式の展開
次の式を展開せよ。
\(\begin{split}{\small (1)}~~(3x-2)^2\end{split}\)
\(\begin{split}{\small (2)}~~(2x+5)(2x-1)\end{split}\)
\(\begin{split}{\small (3)}~~(5x+7y)^2\end{split}\)
\(\begin{split}{\small (4)}~~(2a+3b)(2a-3b)\end{split}\)
\(\begin{split}{\small (5)}~~(x+y-5)(x+y+1)\end{split}\)
\(\begin{split}{\small (6)}~~(a-b+3)^2\end{split}\)
\(\begin{split}{\small (7)}~~2x(x+1)-(x-2)(x+3)\end{split}\)
\(\begin{split}{\small (8)}~~(a-3)(a+3)-(a-5)^2\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~9x^2-12x+4\)
\({\small (2)}~4x^2+8x-5\)
\({\small (3)}~25x^2+70xy+49y^2\)
\({\small (4)}~4a^2-9b^2\)
\({\small (5)}~x^2+2xy+y^2-4x-4y-5\)
\({\small (6)}~a^2-2ab+b^2+6a-6b+9\)
\({\small (7)}~x^2+x+6\)
\({\small (8)}~10a-34\)

共通因数と因数分解
次の式を因数分解せよ。
\(\begin{split}{\small (1)}~~x^2-5x\end{split}\)
\(\begin{split}{\small (2)}~~6a^2b-4ab^2\end{split}\)
\(\begin{split}{\small (3)}~~15x^2y-10xy^2+5xy\end{split}\)
\(\begin{split}{\small (4)}~~4a^3+8a^2-2a\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~x(x-5)\)
\({\small (2)}~2ab(3a-2b)\)
\({\small (3)}~5xy(3x-2y+1)\)
\({\small (4)}~2a(2a^2+4a-1)\)

因数分解の公式①(和と積)
次の式を因数分解せよ。
\(\begin{split}{\small (1)}~~x^2+5x+6\end{split}\)
\(\begin{split}{\small (2)}~~x^2+5x-14\end{split}\)
\(\begin{split}{\small (3)}~~x^2-2x-15\end{split}\)
\(\begin{split}{\small (4)}~~a^2-6a+5\end{split}\)
\(\begin{split}{\small (5)}~~x^2+4x-12\end{split}\)
\(\begin{split}{\small (6)}~~x^2-x-42\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~(x+2)(x+3)\)
\({\small (2)}~(x-2)(x+7)\)
\({\small (3)}~(x+3)(x-5)\)
\({\small (4)}~(a-1)(a-5)\)
\({\small (5)}~(x-2)(x+6)\)
\({\small (6)}~(x+6)(x-7)\)

因数分解の公式②(2乗の式)
次の式を因数分解せよ。
\(\begin{split}{\small (1)}~~x^2+6x+9\end{split}\)
\(\begin{split}{\small (2)}~~a^2-10a+25\end{split}\)
\(\begin{split}{\small (3)}~~x^2-14x+49\end{split}\)
\(\begin{split}{\small (4)}~~x^2-81\end{split}\)
\(\begin{split}{\small (5)}~~x^2-\frac{\,1\,}{\,4\,}\end{split}\)
\(\begin{split}{\small (6)}~~9-y^2\end{split}\)
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~(x+3)^2\end{split}\)
\(\begin{split}{\small (2)}~(a-5)^2\end{split}\)
\(\begin{split}{\small (3)}~(x-7)^2\end{split}\)
\(\begin{split}{\small (4)}~(x+9)(x-9)\end{split}\)
\(\begin{split}{\small (5)}~\left(x+\frac{\,1\,}{\,2\,}\right)\left(x-\frac{\,1\,}{\,2\,}\right)\end{split}\)
\(\begin{split}{\small (6)}~(3+y)(3-y)\end{split}\)

いろいろな因数分解①(共通因数)
次の式を因数分解せよ。
\(\begin{split}{\small (1)}~~3x^2-3x-6\end{split}\)
\(\begin{split}{\small (2)}~~5ax^2-45a\end{split}\)
\(\begin{split}{\small (3)}~~2a^2+20a+50\end{split}\)
\(\begin{split}{\small (4)}~~9x^2+6x+1\end{split}\)
\(\begin{split}{\small (5)}~~16x^2-24xy+9y^2\end{split}\)
\(\begin{split}{\small (6)}~~9a^2-16b^2\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~3(x-2)(x+1)\)
\({\small (2)}~2a(x+3)(x-3)\)
\({\small (3)}~2(a+5)^2\)
\({\small (4)}~(3x+1)^2\)
\({\small (5)}~(4x-3y)^2\)
\({\small (6)}~(3a+4b)(3a-4b)\)

いろいろな因数分解②(共通部分)
次の式を因数分解せよ。
\(\begin{split}{\small (1)}~~(x+y)a-(x+y)b\end{split}\)
\(\begin{split}{\small (2)}~~(x+1)^2-(x+1)-72\end{split}\)
\(\begin{split}{\small (3)}~~(x-3)^2-64\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~(x+y)(a-b)\)
\({\small (2)}~(x-8)(x+9)\)
\({\small (3)}~(x+5)(x-11)\)

展開・因数分解を利用した計算
次の式をくふうして計算せよ。
\(\begin{split}{\small (1)}~~98^2\end{split}\)
\(\begin{split}{\small (2)}~~53{\, \small \times \,}47\end{split}\)
\(\begin{split}{\small (3)}~~35^2-15^2\end{split}\)
\(\begin{split}{\small (4)}~~11{\, \small \times \,}13+17{\, \small \times \,}11\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~9604\) \({\small (2)}~2491\)
\({\small (3)}~1000\) \({\small (4)}~330\)

展開・因数分解と式の値
次の問いに答えよ。
\({\small (1)}~\)\(a=1.2\) のとき、
式 \(a(a-3)-(a-4)^2\) の値を求めよ。
\({\small (2)}~\)\(x=18\) のとき、
式 \(x^2-6x-16\) の値を求めよ。
\({\small (3)}~\)\(a=6.8~,~b=3.2\) のとき、
式 \(a^2-b^2\) の値を求めよ。
\({\small (4)}~\)\(x=87~,~y=-13\) のとき、
式 \(x^2-2xy+y^2\) の値を求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~-10\) \({\small (2)}~200\)
\({\small (3)}~36\) \({\small (4)}~10000\)

展開・因数分解と数の性質
次のことを証明せよ。
\({\small (1)}~\)連続する3つの整数では、真ん中の数の2乗から小さい方の数と大きい方の数の積を引くと \(1\) となる。
\({\small (2)}~\)連続する2つの奇数では、大きい方の数の2乗から小さい方の数の2乗を引くと \(8\) の倍数となる。
\({\small (3)}~\)連続する2つの偶数の積に \(1\) を加えると、2つの偶数の間の奇数の2乗となる。
[ 解答を見る ]
【解答】
\({\small (1)}\)[証明] 連続する3つの整数を整数 \(n\) を使って、
\(~~~n~,~n+1~,~n+2\)
と表される
このとき、真ん中の数の2乗から小さい方の数と大きい方の数の積を引いたものは、
\(~~~~~~(n+1)^2-n\times (n+2)\)
これを展開すると、
\(\begin{split}~~=~&(n^2+2n+1)-(n^2+2n)\\[2pt]~~=~&n^2+2n+1-n^2-2n\\[2pt]~~=~&1\end{split}\)
したがって、連続する3つの整数では、真ん中の数の2乗から小さい方の数と大きい方の数の積を引くと \(1\) となる [終]
【別解】
[証明] 連続する3つの整数を整数 \(n\) を使って、
\(~~~n-1~,~n~,~n+1\)
と表される
このとき、真ん中の数の2乗から小さい方の数と大きい方の数の積を引いたものは、
\(\begin{split}&n^2-(n-1)\times (n+1)\\[2pt]~~=~&n^2-(n-1)(n+1)\end{split}\)
これを展開すると、
\(\begin{split}~~=~&n^2-(n^2-1)\\[2pt]~~=~&n^2-n^2+1\\[2pt]~~=~&1\end{split}\)
したがって、連続する3つの整数では、真ん中の数の2乗から小さい方の数と大きい方の数の積を引くと \(1\) となる [終]
\({\small (2)}\)[証明] 連続する2つの奇数を整数 \(n\) を使って、
\(~~~2n-1~,~2n+1\)
と表される
このとき、大きい方の数の2乗から小さい方の数の2乗を引いたものは、
\(~~~~~~(2n+1)^2-(2n-1)^2\)
式を展開すると、
\(\begin{split}~~=~&(4n^2+4n+1)-(4n^2-4n+1)\\[2pt]~~=~&4n^2+4n+1-4n^2+4n-1\\[2pt]~~=~&8n\end{split}\)
\(n\) は整数であるから、\(8n\) は \(8\) の倍数である
したがって、連続する2つの奇数では、大きい方の数の2乗から小さい方の数の2乗を引くと \(8\) の倍数となる [終]
\({\small (3)}\)[証明] 連続する2つの偶数を整数 \(n\) を使って、
\(~~~2n~,~2n+2\)
と表される
このとき、これらの積に \(1\) を加えたものは、
\(~~~~~~2n(2n+2)+1\)
式を展開すると、
\(\begin{split}~~=~&4n^2+4n+1\end{split}\)
\(4n^2=(2n)^2\) として因数分解すると、
\(\begin{split}~~=~&(2n)^2+2\times 2\times 1\times n+1^2\\[2pt]~~=~&(2n+1)^2\end{split}\)
\(2n+1\) は、\(2n\) と \(2n+2\) の間の奇数である
したがって、連続する2つの偶数の積に \(1\) を加えると、2つの偶数の間の奇数の2乗となる [終]

展開・因数分解と図形の性質
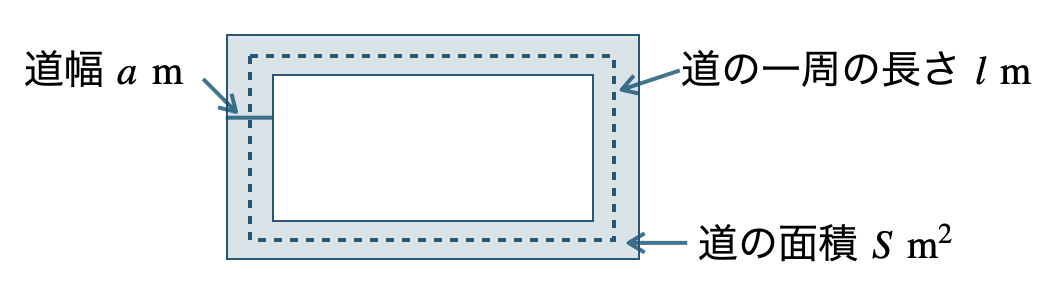
次の図のように、長方形の土地のまわりに幅 \(a~{\rm m}\) の道がある。この道の真ん中を通る線の一周の長さ \(l~{\rm m}\) で道の面積が \(S~{\rm m}^2\) である。
このとき、\(S=al\) が成り立つことを証明せよ。
[ 解答を見る ]
【解答】[証明] 内側の土地の縦の長さを \(x~{\rm m}\) 、横の長さを \(y~{\rm m}\) とすると、
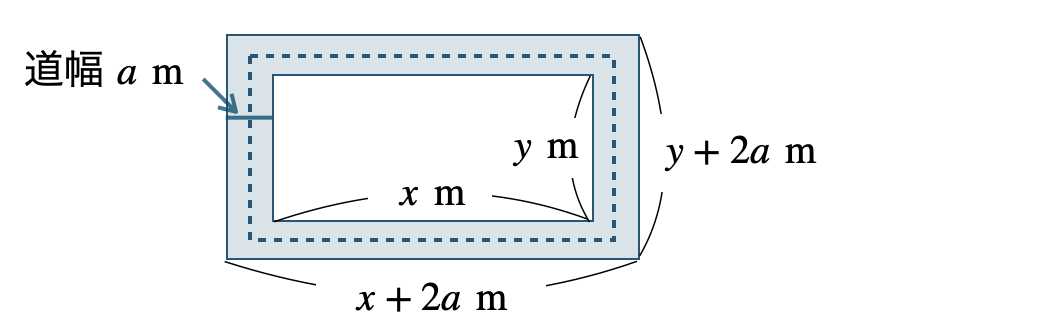
全体の縦の長さが、\(x+a+a=x+2a~[\,{\rm m}\,]\)
横の長さが、\(y+a+a=y+2a~[\,{\rm m}\,]\)
となるので、全体の面積は、
\(\begin{split}&(x+2a)(y+2a)
\\[2pt]~~=~&x{\, \small \times \,} y+x{\, \small \times \,} 2a+2a{\, \small \times \,} y+2a{\, \small \times \,} 2a\\[2pt]~~=~&xy+2ax+2ay+4a^2~[\,{\rm m^2}\,]\end{split}\)
また、内側の面積は、\(x{\, \small \times \,} y=xy~[\,{\rm m^2}\,]\)
である
よって、
道の面積 \(S~{\rm m}^2\) は全体の面積ー内側の土地の面積より、
\(\begin{eqnarray}~~~S&=&(xy+2ax+2ay+4a^2)-xy\\[2pt]~~~&=&(xy-xy)+2ax+2ay+4a^2\\[2pt]~~~&=&2ax+2ay+4a^2\\[2pt]~~~&=&a{\, \small \times \,} 2x+a{\, \small \times \,} 2y +a{\, \small \times \,} 4a\\[2pt]~~~&=&a(2x+2y+4a)~[\,{\rm m^2}\,]\end{eqnarray}\)
次に、道の真ん中を通る線の一周の長さ \(l~{\rm m}\) は、
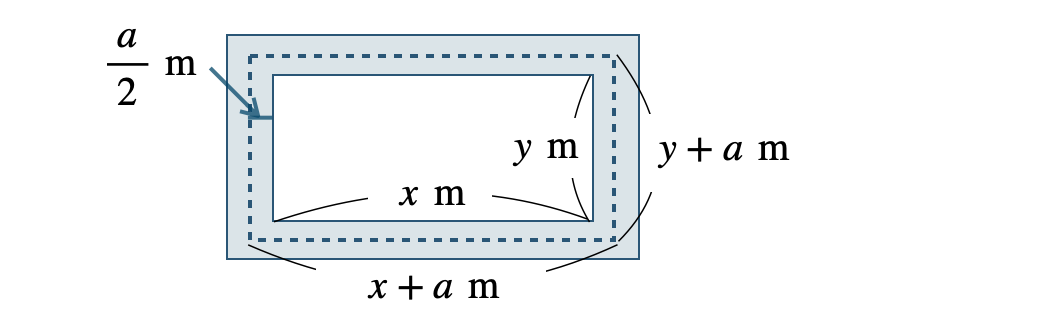
縦の長さが、
\(\begin{split}&x+\frac{\,a \,}{\,2 \,}+\frac{\,a \,}{\,2 \,}\\[3pt]~~=~&x+\frac{\,a+a \,}{\,2 \,}=x+\frac{\,2a \,}{\,2 \,}=x+a~[\,{\rm m}\,]\end{split}\)
横の長さが、
\(\begin{split}&y+\frac{\,a \,}{\,2 \,}+\frac{\,a \,}{\,2 \,}\\[3pt]~~=~&y+\frac{\,a+a \,}{\,2 \,}=y+\frac{\,2a \,}{\,2 \,}=y+a~[\,{\rm m}\,]\end{split}\)
一周の長さは、縦の長さ×2+横の長さ×2より、
\(\begin{eqnarray}~~~l&=&2(x+a)+2(y+a)\\[2pt]~~~&=&2x+2a+2y+2a\\[2pt]~~~&=&2x+2y+(2a+2a)\\[2pt]~~~&=&2x+2y+4a~[\,{\rm m}\,]\end{eqnarray}\)
したがって、
\(~~~~~S=a(2x+2y+4a)\)
\(~~~~~l=2x+2y+4a\)
であるので、\(S=al\)が成り立つ。[終]

展開・因数分解と表やカレンダー
次の問いに答えよ。
\({\small (1)}~\)下の図1は、自然数が順番に一段5つずつ並んでいる。このとき、表の中の4つの整数の組(図2)について、\(bc-ad\) の値はつねに \(5\) となることを証明せよ。
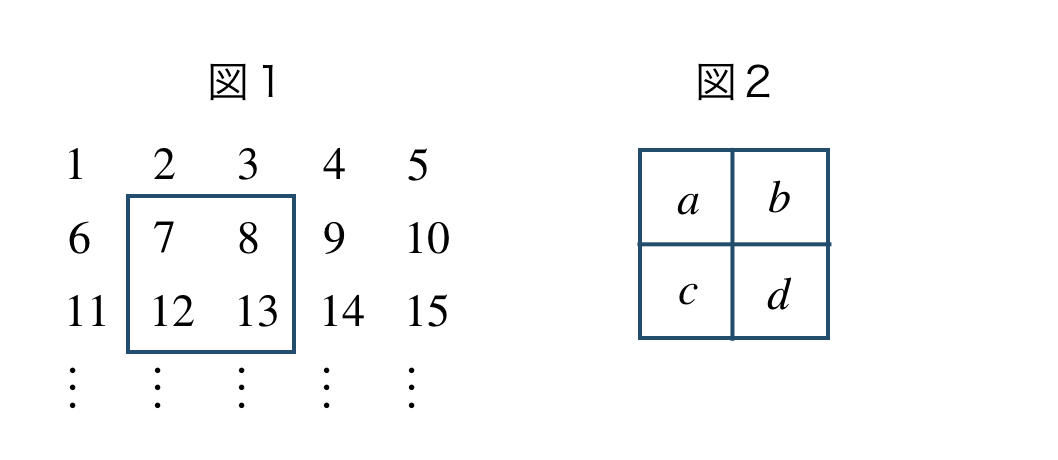
\({\small (2)}~\)下の図3は、ある月のカレンダーである。このとき、カレンダーの中の3つの整数の組(図4)について、\(b^2-ac\) の値はつねに \(49\) となることを証明せよ。
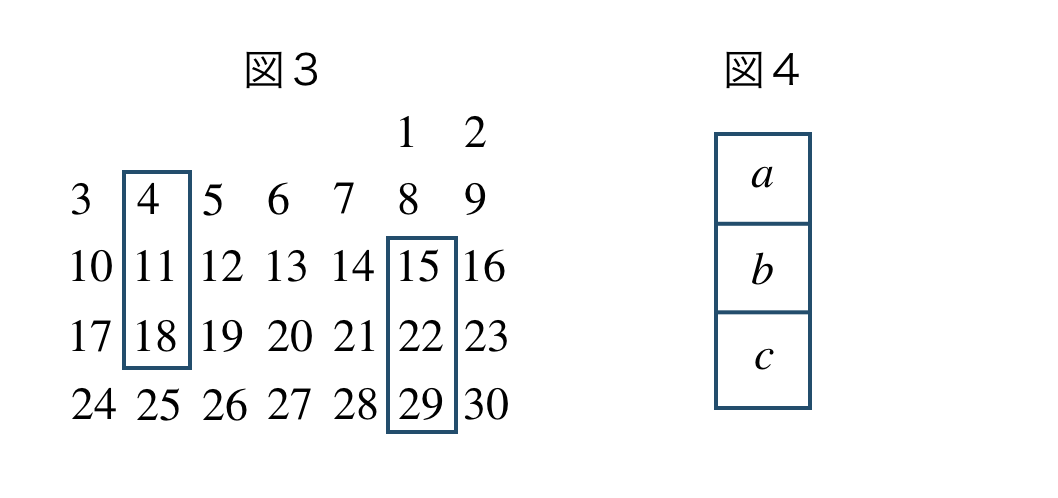
[ 解答を見る ]
【解答】
\({\small (1)}~\)[証明] 整数\(n\) を用いて、\(a=n\) とすると、
\(b\) は \(a\) の右隣りで \(+1\) されて、\(b=n+1\)
\(c\) は \(a\) の一段下で \(+5\) されて、\(c=n+5\)
\(d\) は \(a\) の一段下の右隣りで \(+6\) されて、\(d=n+6\)

よって、\(bc-ad\) は、
※ ( ) を付けたまま代入する。
\(\begin{split}&bc-ad\\[2pt]~~=~&(n+1)(n+5)-n(n+6)\end{split}\)
それぞれを展開すると、
\(\begin{split}~~=~&(n^2+6n+5)-(n^2+6n)\\[2pt]~~=~&n^2+6n+5-n^2-6n\\[2pt]~~=~&(n^2-n^2)+(6n-6n)+5\\[2pt]~~=~&5\end{split}\)
したがって、\(bc-ad\) の値はつねに \(5\) となる [終]
\({\small (2)}~\)[証明] 整数\(n\) を用いて、\(b=n\) とすると、
\(a\) は \(b\) の一段上で \(-7\) されて、\(a=n-7\)
\(c\) は \(b\) の一段下で \(+7\) されて、\(c=n+7\)

よって、\(b^2-ac\) は、
※ ( ) を付けたまま代入する。
\(\begin{split}&b^2-ac\\[2pt]~~=~&n^2-(n-7)(n+7)\end{split}\)
展開すると、
\(\begin{split}~~=~&n^2-(n^2-49)\\[2pt]~~=~&n^2-n^2+49\\[2pt]~~=~&49\end{split}\)
したがって、\(b^2-ac\) の値はつねに \(49\) となる [終]



