このページは「中学数学3 2次方程式」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう!
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
【問題一覧】中学数学3 2次方程式
2次方程式の解
次の問いに答えよ。
\({\small (1)}~\)次の方程式のうち2次方程式であるものを選び、\(ax^2+bx+c=0\) の \(a~,~b~,~c\) にあたる数をそれぞれ答えよ。
① \(\begin{split}x^2-3x+5=0\end{split}\)
② \(\begin{split}2x-1=8\end{split}\)
③ \(\begin{split}3x^2-5x+1=x^2+3\end{split}\)
④ \(\begin{split}x(x-1)=x^2+6\end{split}\)
\({\small (2)}~-2~,~-1~,~0~,~1~,~2~,~3\) のうち、次の2次方程式の解であるものをすべて選べ。
① \(\begin{split}x^2-5x+6=0\end{split}\)
② \(\begin{split}x^2+2x=0\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① 2次方程式となる
\(a=1~,~b=-3~,~c=5\)
② 2次方程式でない
③ 2次方程式となる
\(a=2~,~b=-5~,~c=-2\)
④ 2次方程式でない
\({\small (2)}~\)
① \(x=2~,~3\)
② \(x=-2~,~0\)

因数分解と2次方程式①
次の方程式を解け。
\(\begin{split}{\small (1)}~~(x+1)(x-4)=0\end{split}\)
\(\begin{split}{\small (2)}~~x^2+x-2=0\end{split}\)
\(\begin{split}{\small (3)}~~x^2+5x+4=0\end{split}\)
\(\begin{split}{\small (4)}~~x^2=8x-15\end{split}\)
\(\begin{split}{\small (5)}~~x^2-25=0\end{split}\)
\(\begin{split}{\small (6)}~~x^2-49=0\end{split}\)
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~~x=-1~,~4\end{split}\)
\(\begin{split}{\small (2)}~~x=-2~,~1\end{split}\)
\(\begin{split}{\small (3)}~~x=-1~,~-4\end{split}\)
\(\begin{split}{\small (4)}~~x=3~,~5\end{split}\)
\(\begin{split}{\small (5)}~~x=\pm\,5\end{split}\)
\(\begin{split}{\small (6)}~~x=\pm\,7\end{split}\)

因数分解と2次方程式②
次の方程式を解け。
\(\begin{split}{\small (1)}~~x^2-x=0\end{split}\)
\(\begin{split}{\small (2)}~~2x^2+10x=0\end{split}\)
\(\begin{split}{\small (3)}~~3x^2=21x\end{split}\)
\(\begin{split}{\small (4)}~~x^2-4x+4=0\end{split}\)
\(\begin{split}{\small (5)}~~x^2+10x+25=0\end{split}\)
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~~x=0~,~1\end{split}\)
\(\begin{split}{\small (2)}~~x=0~,~-5\end{split}\)
\(\begin{split}{\small (3)}~~x=0~,~7\end{split}\)
\(\begin{split}{\small (4)}~~x=2\end{split}\)
\(\begin{split}{\small (5)}~~x=-5\end{split}\)

平方根での2次方程式の解き方
次の方程式を解け。
\(\begin{split}{\small (1)}~~x^2=9\end{split}\)
\(\begin{split}{\small (2)}~~3x^2=12\end{split}\)
\(\begin{split}{\small (3)}~~x^2-5=0\end{split}\)
\(\begin{split}{\small (4)}~~25x^2=7\end{split}\)
\(\begin{split}{\small (5)}~~4x^2-8=1\end{split}\)
\(\begin{split}{\small (6)}~~9x^2+2=10\end{split}\)
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~~x=\pm\,3\end{split}\)
\(\begin{split}{\small (2)}~~x=\pm\,2\end{split}\)
\(\begin{split}{\small (3)}~~x=\pm\,\sqrt{5}\end{split}\)
\(\begin{split}{\small (4)}~~x=\pm\,\frac{\,\sqrt{7}\,}{\,5\,}\end{split}\)
\(\begin{split}{\small (5)}~~x=\pm\,\frac{\,3\,}{\,2\,}\end{split}\)
\(\begin{split}{\small (6)}~~x=\pm\,\frac{\,2\sqrt{2}\,}{\,3\,}\end{split}\)

2乗の形の2次方程式
次の方程式を解け。
\(\begin{split}{\small (1)}~~(x+1)^2=4\end{split}\)
\(\begin{split}{\small (2)}~~(x-2)^2=3\end{split}\)
\(\begin{split}{\small (3)}~~(x-3)^2-7=0\end{split}\)
\(\begin{split}{\small (4)}~~(x-4)^2-8=0\end{split}\)
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~~x=1~,~-3\end{split}\)
\(\begin{split}{\small (2)}~~x=2\pm\,\sqrt{3}\end{split}\)
\(\begin{split}{\small (3)}~~x=3\pm\,\sqrt{7}\end{split}\)
\(\begin{split}{\small (4)}~~x=4\pm\,2\sqrt{2}\end{split}\)

因数分解できない2次方程式
次の方程式を解け。
\(\begin{split}{\small (1)}~~x^2+2x=2\end{split}\)
\(\begin{split}{\small (2)}~~x^2-4x-4=0\end{split}\)
\(\begin{split}{\small (3)}~~x^2+6x+4=0\end{split}\)
\(\begin{split}{\small (4)}~~x^2+3x=1\end{split}\)
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~~x=-1\pm\,\sqrt{3}\end{split}\)
\(\begin{split}{\small (2)}~~x=2\pm\,2\sqrt{2}\end{split}\)
\(\begin{split}{\small (3)}~~x=-3\pm\,\sqrt{5}\end{split}\)
\(\begin{split}{\small (4)}~~x=\frac{\,-3\pm\,\sqrt{13}\,}{\,2\,}\end{split}\)

2次方程式と解の公式
次の方程式を解け。
\(\begin{split}{\small (1)}~~x^2+5x+3=0\end{split}\)
\(\begin{split}{\small (2)}~~2x^2-3x-1=0\end{split}\)
\(\begin{split}{\small (3)}~~x^2+6x+4=0\end{split}\)
\(\begin{split}{\small (4)}~~4x^2+4x-11=0\end{split}\)
\(\begin{split}{\small (5)}~~2x^2+5x-3=0\end{split}\)
\(\begin{split}{\small (6)}~~3x^2-11x-4=0\end{split}\)
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~~x=\frac{\,-5\pm\sqrt{13}\,}{\,2\,}\end{split}\)
\(\begin{split}{\small (2)}~~x=\frac{\,3\pm\sqrt{17}\,}{\,4\,}\end{split}\)
\(\begin{split}{\small (3)}~~x=-3\pm\sqrt{5}\end{split}\)
\(\begin{split}{\small (4)}~~x=\frac{\,-1\pm2\sqrt{3}\,}{\,2\,}\end{split}\)
\(\begin{split}{\small (5)}~~x={ \frac{\,1\,}{\,2\,}}~,~-3\end{split}\)
\(\begin{split}{\small (6)}~~x=4~,~-{ \frac{\,1\,}{\,3\,}}\end{split}\)

いろいろな2次方程式
次の方程式を解け。
\(\begin{split}{\small (1)}~~x(x+2)=3\end{split}\)
\(\begin{split}{\small (2)}~~(x+6)(x-1)=3x-2\end{split}\)
\(\begin{split}{\small (3)}~~(x+9)^2=2(3x+23)\end{split}\)
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~~x=-3~,~1\end{split}\)
\(\begin{split}{\small (2)}~~x=-1\pm\sqrt{5}\end{split}\)
\(\begin{split}{\small (3)}~~x=-5~,~-7\end{split}\)

解が与えられた2次方程式
次の問いに答えよ。
\({\small (1)}~\)\(x\) の2次方程式 \(x^2+ax-10=0\) の解の1つが \(2\) のとき、\(a\) の値ともう1つの解を求めよ。
\({\small (2)}~\)\(x\) の2次方程式 \(x^2-2x+a=0\) の解の1つが \(1-\sqrt{2}\) のとき、\(a\) の値ともう1つの解を求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)\(a=3\)、もう1つの解 \(x=-5\)
\({\small (2)}~\)\(a=-1\)、もう1つの解 \(x=1+\sqrt{2}\)

2次方程式と整数
次の問いに答えよ。
\({\small (1)}~\)大小2つの正の整数があり、差が \(2\) で積が \(35\) である。このとき、この2つの正の整数を求めよ。
\({\small (2)}~\)連続する2つの整数があり、それぞれの2乗の和が \(113\) となる。このとき、この2つの整数を求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)\(5\) と \(7\)
\({\small (2)}~\)\(7\) と \(8\) または \(-8\) と \(-7\)

2次方程式と容積
横の長さが縦の長さより \(5~{\rm cm}\) 長い長方形の紙がある。この紙の四すみから1辺 \(2~{\rm cm}\) の正方形を切り取って、ふたのない箱を作った。
箱の容積が \(132~{\rm cm}^3\) となるとき、もとの長方形の縦の長さと横の長さを求めよ。

[ 解答を見る ]
【解答】
縦の長さ \(10~{\rm cm}\)、横の長さ \(15~{\rm cm}\)

2次方程式と道幅
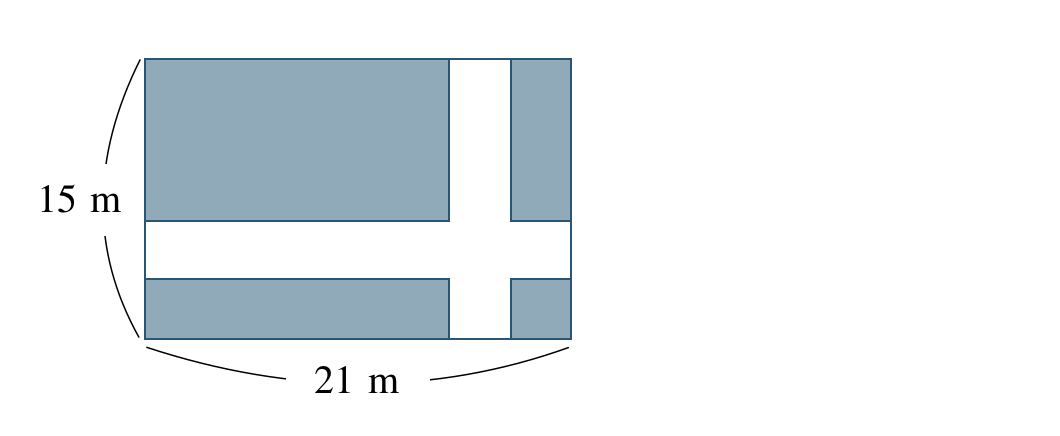
縦の長さが \(15~{\rm m}\)、横の長さが \(21~{\rm m}\) の長方形の土地に図のように道幅が同じで垂直に交わる道を2本つくり、残りの土地を花だんとした。
花だんとした土地の面積を \(280~{\rm m}^2\) とするとき、道幅は何 \({\rm m}\) となるか答えよ。
2次方程式と動く点
図のような正方形 \({\rm ABCD}\) がある。
点 \({\rm P}\) は点 \({\rm A}\) を出発して辺 \({\rm AB}\) を秒速 \(2~{\rm cm}\) で点 \({\rm B}\) まで動く。また、点 \({\rm Q}\) は点 \({\rm P}\) と同時に点 \({\rm B}\) を出発して辺 \({\rm BC}\) を秒速 \(1~{\rm cm}\) で点 \({\rm C}\) まで動く。このとき、\(\triangle {\rm PBQ}\) の面積が \(5~{\rm cm}^2\) になるのは点 \({\rm P~,~Q}\) が出発して何秒後か答えよ。





