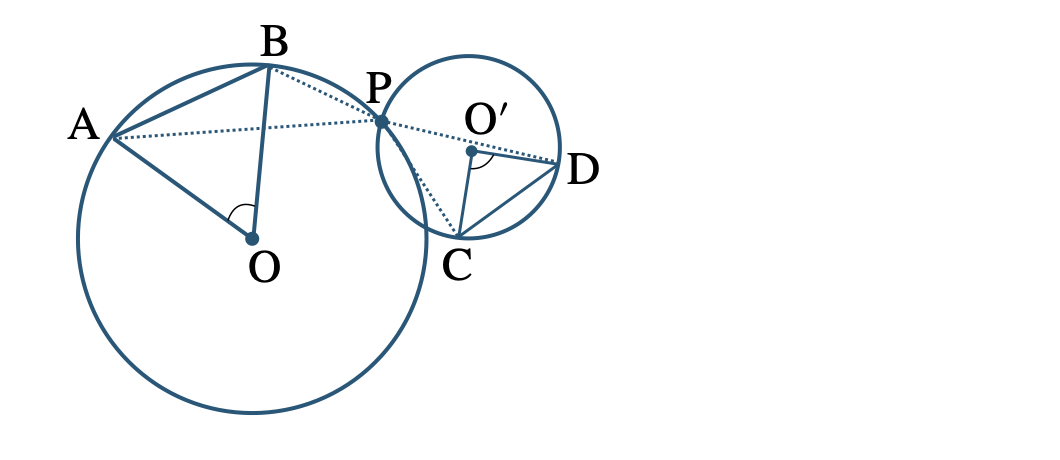啓林館：未来へ広がる数学３

p.164 問1\(\begin{split}{\small (1)}~38^\circ\end{split}\)　　\(\begin{split}{\small (2)}~110^\circ\end{split}\)　　\(\begin{split}{\small (3)}~100^\circ\end{split}\)
\(\begin{split}{\small (4)}~40^\circ\end{split}\)　　\(\begin{split}{\small (5)}~95^\circ\end{split}\)　　\(\begin{split}{\small (6)}~55^\circ\end{split}\)

p.165 問2\(\begin{split}{\small (1)}~36^\circ\end{split}\)　　\(\begin{split}{\small (2)}~65^\circ\end{split}\)

p.165 説明しよう　\(\angle{\rm C}=70^\circ\)
点 \({\rm C}\) のある側の、\(\overset{\frown}{{\rm BD}}\) の円周角の定理より、
　\(x=220^\circ\)
よって、
　\(y=360^\circ-220^\circ=140^\circ\)
点 \({\rm A}\) のある側の、\(\overset{\frown}{{\rm BD}}\) の円周角の定理より、
　\(\angle{\rm C}=140^\circ\div2=70^\circ\)

p.166 問3\(\begin{split}~~~x=28^\circ~,~y=56^\circ\end{split}\)

p.166 問4\(\begin{split}~~~\angle{\rm BQC}=62^\circ\end{split}\)

p.166 説明しよう\(\overset{\frown}{{\rm AC}}\) と \(\overset{\frown}{{\rm CB}}\) に対する円周角が等しいので、
　\(\overset{\frown}{{\rm AC}}=\overset{\frown}{{\rm CB}}\)

p.166 練習問題 1\(\begin{split}{\small (1)}~75^\circ\end{split}\)　　\(\begin{split}{\small (2)}~100^\circ\end{split}\)
\(\begin{split}{\small (3)}~40^\circ\end{split}\)　　\(\begin{split}{\small (4)}~60^\circ\end{split}\)

p.168 説明しよう\(\begin{split}~~~\angle{\rm APB}<\angle{\rm ACB}\end{split}\)

p.169 問1　イ、ウ

p.169 練習問題 1\(\angle{\rm ADB}=\angle{\rm ACB}=33^\circ\) より、同じ円周上にある
\(\begin{split}~~~x=54^\circ~,~y=48^\circ\end{split}\)

p.172 問1

\(\triangle {\rm OAB}\) は正三角形より、
　\(\angle{\rm AOB}=60^\circ\)
円周角の定理より、
　\(\angle{\rm APB}=30^\circ\)

p.172 説明しよう

図のように、\(\angle{\rm CO’D}=90^\circ\) となるような円 \({\rm O’}\)

p.172 問2

① 線分 \({\rm CD}\) を斜辺とする直角二等辺三角形をかき、\({\rm C~,~D}\) 以外の頂点を \({\rm O’}\) とする
② 点 \({\rm O’}\) を中心に、半径 \({\rm CO’}\) の円をかく

p.172 問3

p.173 説明しよう円 \({\rm M}\) の円周角の定理より、\({\rm AO}\) が直径であるので、
　\(\angle{\rm APO}=\angle{\rm AP’O}=90^\circ\)
これより、直線 \({\rm AP~,~AP’}\) は \({\rm OP~,~OP’}\) と垂直に交わるので、円 \({\rm O}\) の接線となる

p.173 問4

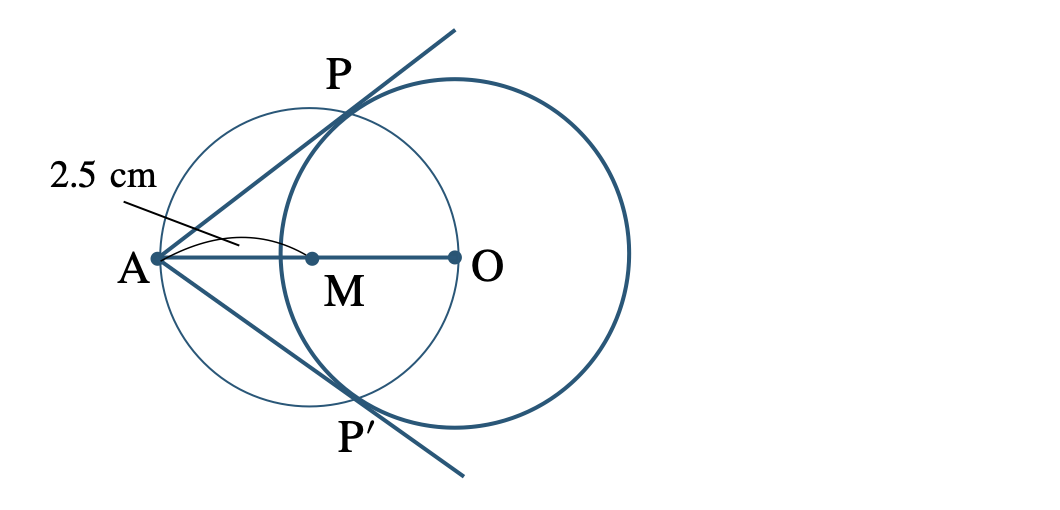
① 線分 \({\rm AO}\) 上に、点 \({\rm A}\) から \(2.5~{\rm cm}\) の位置に点 \({\rm M}\) をとる
※ 線分 \({\rm AO}\) の中点
② 点 \({\rm M}\) を中心に、半径 \(2.5~{\rm cm}\) の円をかく
③ ２つの円の交点を \({\rm P~,~P’}\) とすると、直線 \({\rm AP~,~AP’}\) が接線となる

p.174 問5[証明] \(\triangle {\rm ABE}\) と \(\triangle {\rm ACD}\) において、
\(\overset{\frown}{{\rm ED}}\) の円周角より、
　\(\angle{\rm EBD}=\angle{\rm ECD}\)
よって、
　\(\angle{\rm EBA}=\angle{\rm DCA}~~~\cdots{\large ①}\)
共通の角より、
　\(\angle{\rm EAB}=\angle{\rm DAC}~~~\cdots{\large ②}\)
①、②より、２組の角がそれぞれ等しいので、
　\(\triangle {\rm ABE}\,\,\unicode{x223D}\,\,\triangle {\rm ACD}\)
[終]

p.174 問6\({\small (1)}~\)[証明] \({\rm AD\,//\,BC}\) より、錯角が等しいので、
　\(\angle{\rm ADB}=\angle{\rm DBC}\)
\(\overset{\frown}{{\rm AB}}\) と \(\overset{\frown}{{\rm CD}}\) に対する円周角が等しいので、
　\(\overset{\frown}{{\rm AB}}=\overset{\frown}{{\rm CD}}\)
[終]

---

\({\small (2)}~\)成り立つ