このページは教科書改訂(令和7年度、2025年度)に対応済みの内容です。
このページは、数研出版:これからの数学1
4章 比例と反比例(令和7年度対応)
4章 比例と反比例(令和7年度対応)

教科書に完全対応の問題集|教科書ぴったりトレーニング
教科書に対応した数学の問題集|教科書ぴったりトレーニングの紹介 こんにちは、みなさん!今回は中学生の...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
数研出版中1 1章 正の数と負の数(令和7年度対応)
数研出版中1 2章 文字と式(令和7年度対応)
数研出版中1 3章 1次方程式(令和7年度対応)
数研出版中1 4章 比例と反比例(令和7年度対応)
数研出版中1 5章 平面図形(令和7年度対応)
数研出版中1 6章 空間図形
数研出版中1 7章 データの活用
4章 比例と反比例
1 比例
1 関数
p.125 問1 ア、エ、オ
■ 同じタイプの例題解説
» 変数と関数
» 変数と関数
p.126 問2\(\begin{split}{\small (1)}~x< 0\end{split}\) \(\begin{split}{\small (2)}~x≧-1\end{split}\)
\(\begin{split}{\small (3)}~-3≦x≦5\end{split}\)
\(\begin{split}{\small (3)}~-3≦x≦5\end{split}\)
■ 同じタイプの例題解説
» 変域の表し方
» 変域の表し方
2 比例
p.129 問2\({\small (1)}~y\) の値
\(\begin{split}~~~\cdots ~,~16~,~12~,~8~,~4~,~0~,~\end{split}\)
\(\begin{split}~~~~~~-4~,~-8~,~-12~,~-16~,~\cdots\end{split}\)
\({\small (2)}~\)\(2\) 倍、\(3\) 倍、\(4\) 倍…となる
\({\small (3)}~\)比例定数 \(-4\)
\(\begin{split}~~~\cdots ~,~16~,~12~,~8~,~4~,~0~,~\end{split}\)
\(\begin{split}~~~~~~-4~,~-8~,~-12~,~-16~,~\cdots\end{split}\)
\({\small (2)}~\)\(2\) 倍、\(3\) 倍、\(4\) 倍…となる
\({\small (3)}~\)比例定数 \(-4\)
■ 同じタイプの例題解説
» 比例の関係
» 比例の関係
p.130 問3\(\begin{split}{\small (1)}~y=5x\end{split}\) \(\begin{split}{\small (2)}~y=-15\end{split}\)
\(\begin{split}{\small (3)}~x=4\end{split}\)
\(\begin{split}{\small (3)}~x=4\end{split}\)
■ 同じタイプの例題解説
» 比例の式
» 比例の式
3 座標
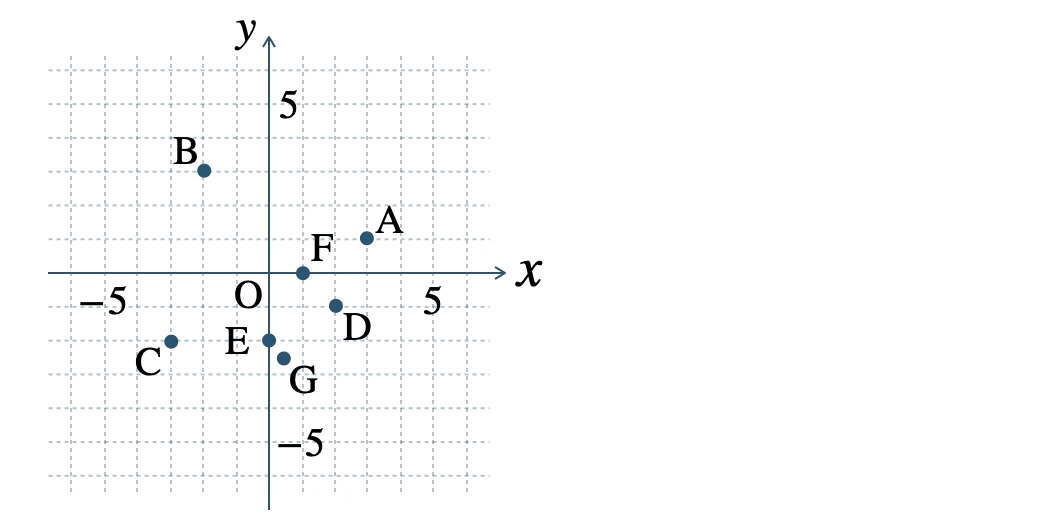
p.133 問1\(\begin{split}~~~{\rm A}(3~,~2)~,~{\rm B}(-3~,~1)~,~{\rm C}(2~,~-2)\end{split}\)
\(\begin{split}~~~{\rm D}(-2~,~-3)~,~{\rm E}(-2~,~0)~,~{\rm F}(0~,~1)\end{split}\)
\(\begin{split}~~~{\rm D}(-2~,~-3)~,~{\rm E}(-2~,~0)~,~{\rm F}(0~,~1)\end{split}\)
■ 同じタイプの例題解説
» 座標と点の表し方
» 座標と点の表し方
4 比例のグラフ
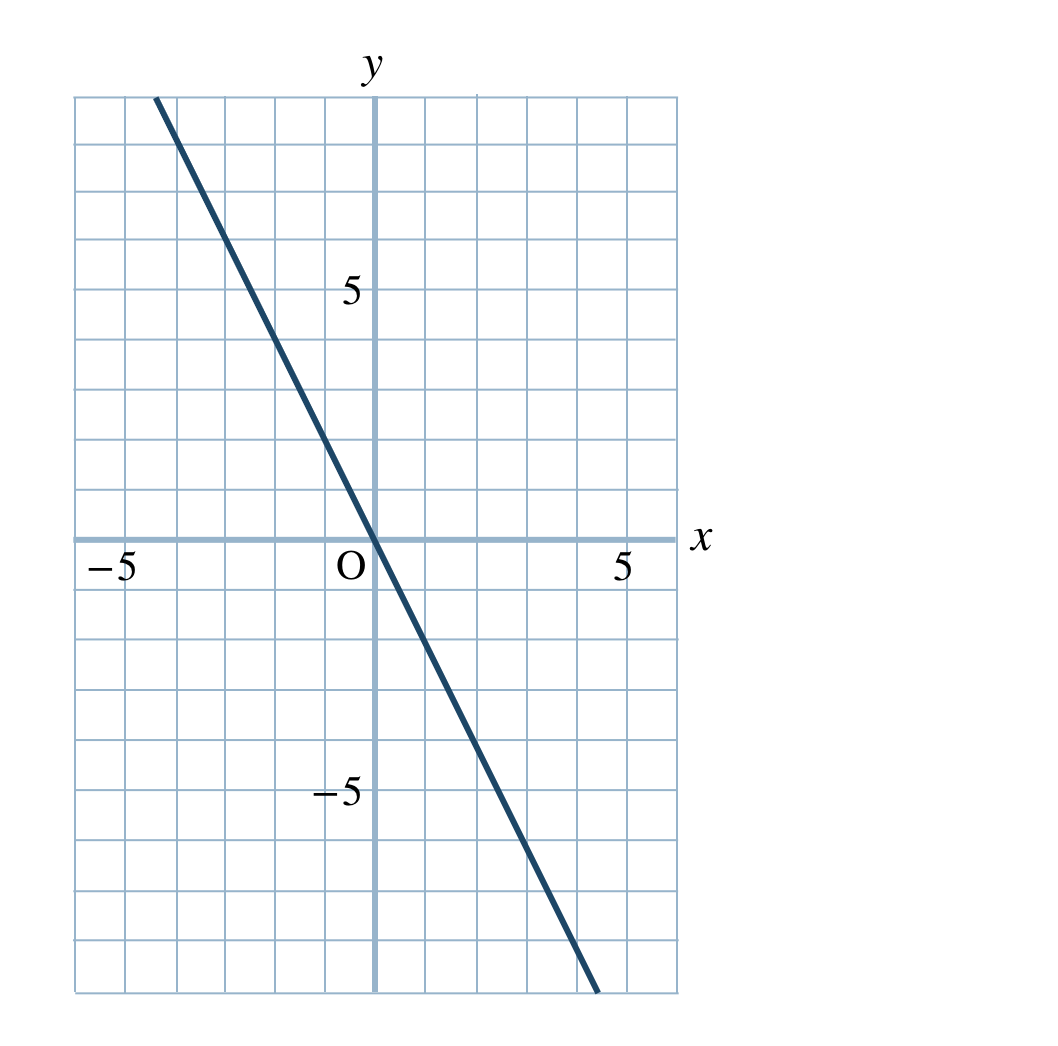
p.134 問1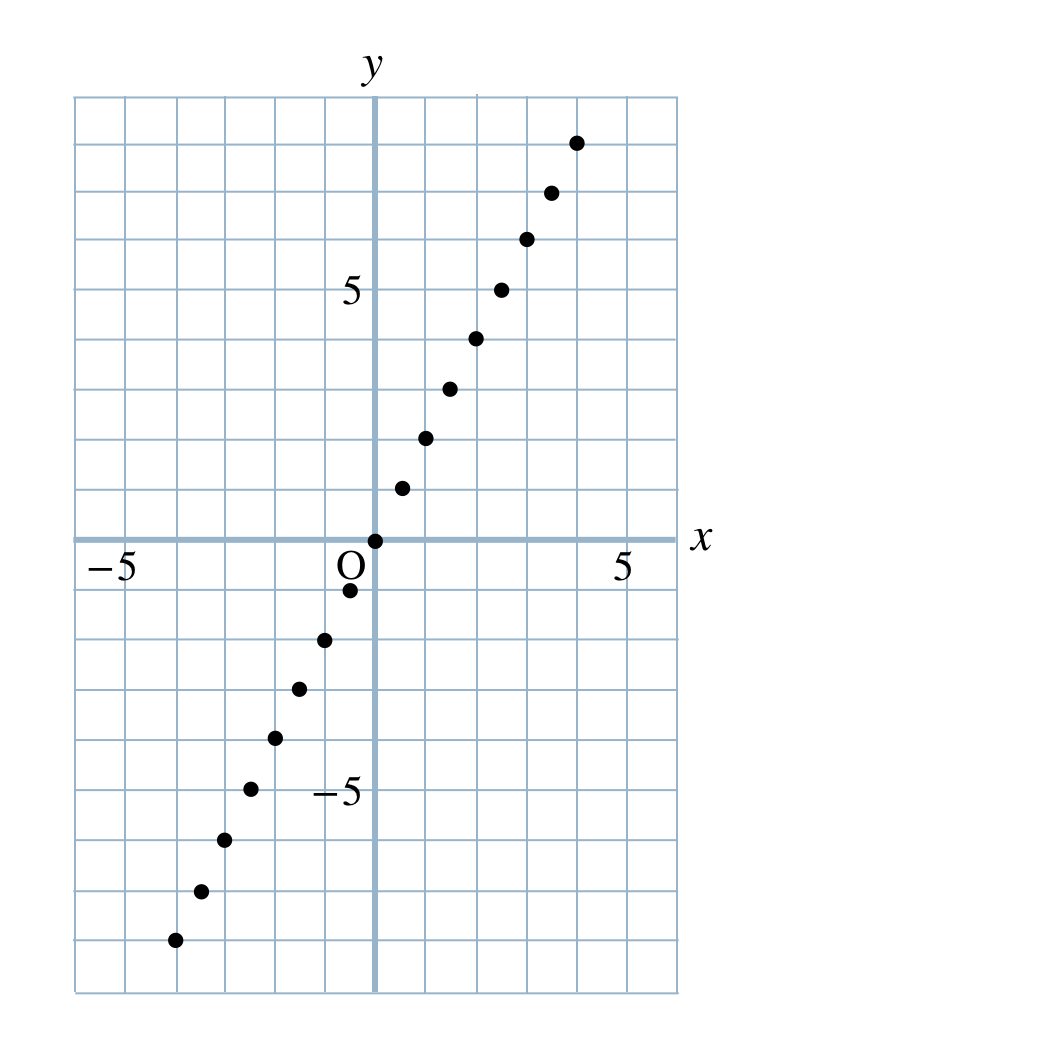

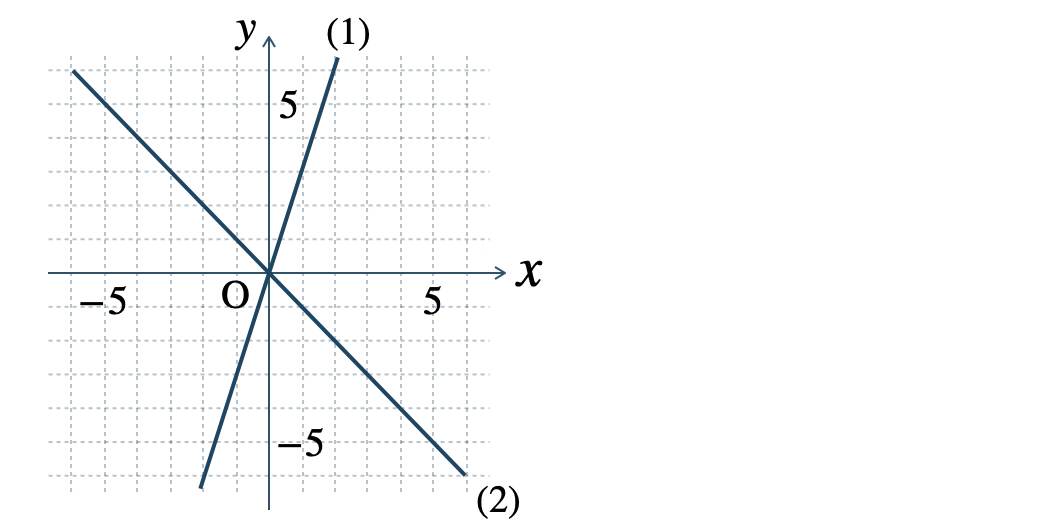
p.137 問4\({\small (1)}~\)

\({\small (2)}~\)
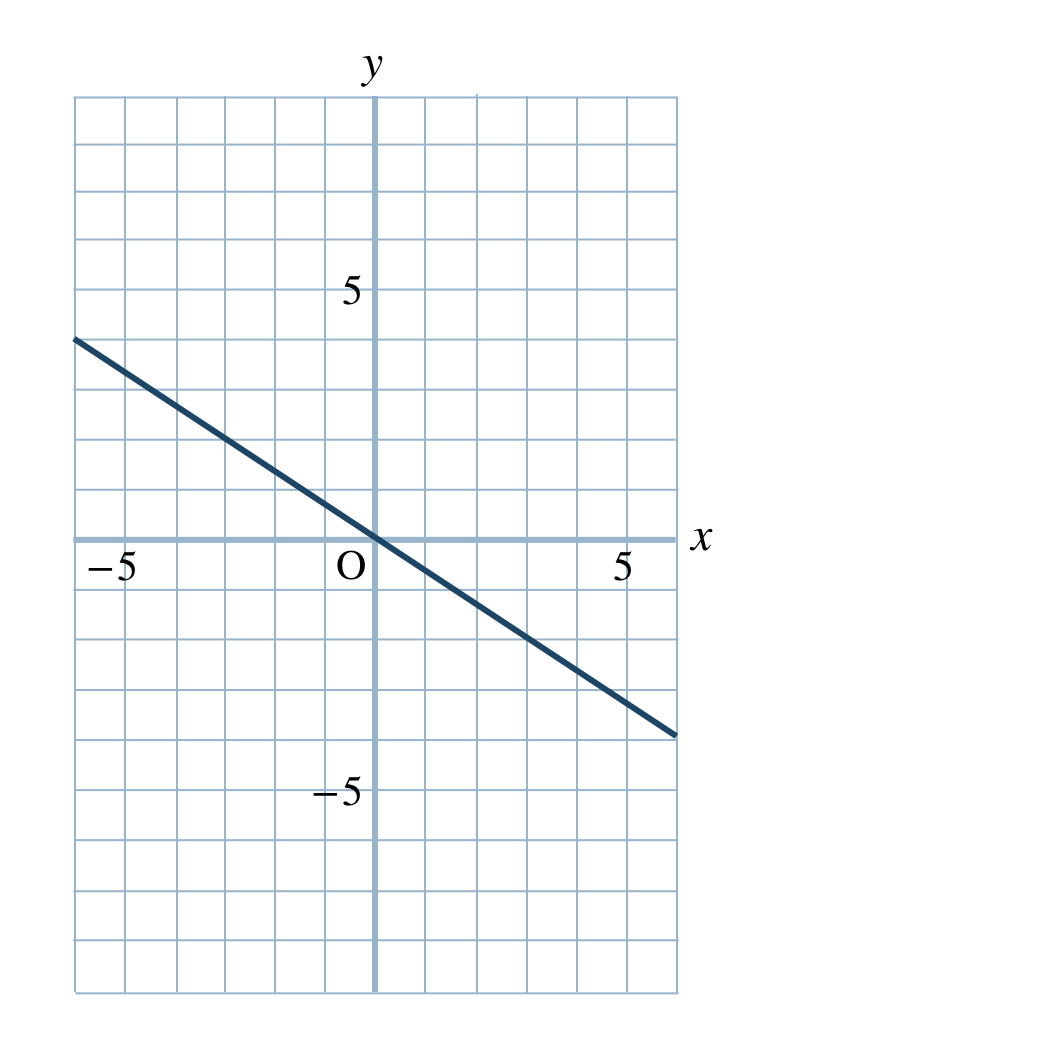

\({\small (2)}~\)

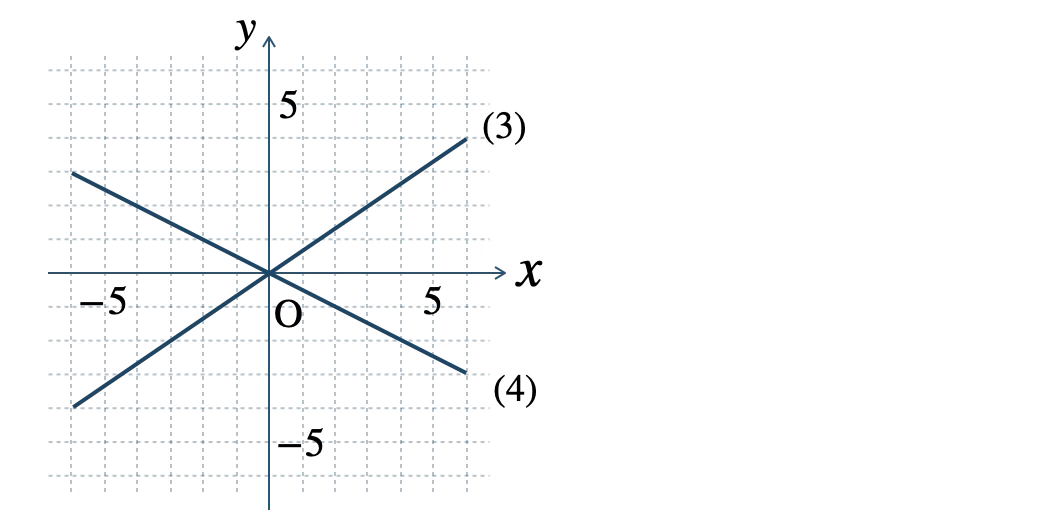
p.137 問5
\(\begin{split}{\small (1)}~y=3x\end{split}\) \(\begin{split}{\small (2)}~y=\frac{\,3\,}{\,4\,}x\end{split}\)
\(\begin{split}{\small (3)}~y=-x\end{split}\) \(\begin{split}{\small (4)}~y=-\frac{\,3\,}{\,2\,}x\end{split}\)
\(\begin{split}{\small (1)}~y=3x\end{split}\) \(\begin{split}{\small (2)}~y=\frac{\,3\,}{\,4\,}x\end{split}\)
\(\begin{split}{\small (3)}~y=-x\end{split}\) \(\begin{split}{\small (4)}~y=-\frac{\,3\,}{\,2\,}x\end{split}\)
■ 同じタイプの例題解説
» グラフと比例・反比例の式
» グラフと比例・反比例の式
2 反比例
1 反比例
p.140 問1
\(\begin{split}{\small (1)}~y={\frac{\,8\,}{\,x\,}}\end{split}\) より、\(y\) は \(x\) に反比例する
また、比例定数は \(8\)
\(\begin{split}{\small (2)}~y={\frac{\,20\,}{\,x\,}}\end{split}\) より、\(y\) は \(x\) に反比例する
また、比例定数は \(20\)
\(\begin{split}{\small (1)}~y={\frac{\,8\,}{\,x\,}}\end{split}\) より、\(y\) は \(x\) に反比例する
また、比例定数は \(8\)
\(\begin{split}{\small (2)}~y={\frac{\,20\,}{\,x\,}}\end{split}\) より、\(y\) は \(x\) に反比例する
また、比例定数は \(20\)
■ 同じタイプの例題解説
» 反比例の関係
» 反比例の関係
p.141 問2\(y\) の値は、
\(\begin{split}~~~\cdots~,~2~,~2.4~,~3~,~4~,~6~,~\end{split}\)
\(\begin{split}~~~12~,~×~,~-12~,~-6~,~-4~,~\end{split}\)
\(\begin{split}~~~-3~,~-2.4~,~-2~,~\cdots\end{split}\)
\(\begin{split}~~~\cdots~,~2~,~2.4~,~3~,~4~,~6~,~\end{split}\)
\(\begin{split}~~~12~,~×~,~-12~,~-6~,~-4~,~\end{split}\)
\(\begin{split}~~~-3~,~-2.4~,~-2~,~\cdots\end{split}\)
■ 同じタイプの例題解説
» 反比例の関係
» 反比例の関係
p.142 問3\(\begin{split}~~~y=-8\end{split}\)
■ 同じタイプの例題解説
» 反比例の式
» 反比例の式
p.142 問4
\(\begin{split}{\small (1)}~y=-\frac{\,28\,}{\,x\,}\end{split}\) \(\begin{split}{\small (2)}~\end{split}\)比例定数 \(-28\)
\(\begin{split}{\small (3)}~y=2\end{split}\)
\(\begin{split}{\small (1)}~y=-\frac{\,28\,}{\,x\,}\end{split}\) \(\begin{split}{\small (2)}~\end{split}\)比例定数 \(-28\)
\(\begin{split}{\small (3)}~y=2\end{split}\)
■ 同じタイプの例題解説
» 反比例の式
» 反比例の式
2 反比例のグラフ
p.145 問1

p.146 問2・ちがっているところ
\(~~~x\) の値を大きくするときの \(y\) の値の変わり方
\(~~~\)グラフの位置
・共通しているところ
\(~~~\)グラフの形(双曲線)
\(~~~x\) 軸、\(y\) 軸に重ならない
\(~~~x\) の値を大きくするときの \(y\) の値の変わり方
\(~~~\)グラフの位置
・共通しているところ
\(~~~\)グラフの形(双曲線)
\(~~~x\) 軸、\(y\) 軸に重ならない
■ 同じタイプの例題解説
» 反比例のグラフ
» 反比例のグラフ
3 比例と反比例の利用
p.152 問2\({\small (1)}~750~{\rm m}\) \({\small (2)}~10\) 分後 \({\small (3)}~9\) 分後
■ 同じタイプの例題解説
» 比例の利用
» 比例の利用
次のページ「5章 平面図形」