東京書籍：新しい数学３

p.170 問1\(\begin{split}{\small (1)}~\angle x=50^\circ\end{split}\)　　\(\begin{split}{\small (2)}~\angle x=40^\circ\end{split}\)
\(\begin{split}{\small (3)}~\angle x=240^\circ\end{split}\)

p.171 問2[証明] \(\triangle {\rm OAB}\) と \(\triangle {\rm OCD}\) において、
\(\overset{\frown}{\rm AB}=\overset{\frown}{\rm CD}\) より、等しい弧に対する中心角は等しいから、
\(\begin{split}~~~\angle{\rm AOB}=\angle{\rm COD}~~~\cdots{\large ①}\end{split}\)
また、円の半径より、
\(\begin{split}~~~{\rm AO=CO}\cdots{\large ②}\end{split}\)
\(\begin{split}~~~{\rm BO=DO}\cdots{\large ③}\end{split}\)
①、②、③より、２組の辺とその間の角がそれぞれ等しいから、
\(\begin{split}~~~\triangle {\rm OAB}\equiv\triangle {\rm OCD}\end{split}\)
合同な図形の対応する辺は等しいから、
\(\begin{split}~~~{\rm AB=CD}\end{split}\)
[終]

---

いえる
\(\angle{\rm APB}=\angle{\rm CQB}\) より、その中心角も等しいから
\(\begin{split}~~~\angle{\rm AOB}=\angle{\rm COD}\end{split}\)
よって、
\(\begin{split}~~~{\rm AB=CD}\end{split}\)

p.172 問3[証明] 線分ＡＤ、ＢＣを引く
\({\rm AB\,//\,CD}\) より、平行線の錯角は等しいから、
\(\begin{split}~~~\angle{\rm ABC}=\angle{\rm BCD}\end{split}\)
よって、等しい円周角に対する弧は等しいから、
\(\begin{split}~~~\overset{\frown}{\rm AC}=\overset{\frown}{\rm BD}\end{split}\)
[終]

p.172 問4\({\small (1)}~\)[証明] 仮定より、\({\rm AE=BC}\)
これより、他の頂点と逆側の弧 \(\overset{\frown}{\rm AE}~,~\overset{\frown}{\rm BC}\) は、
\(\begin{split}~~~\overset{\frown}{\rm AE}=\overset{\frown}{\rm BC}\end{split}\)
よって、等しい弧に対する円周角は等しいから、
\(\begin{split}~~~\angle{\rm ABE}=\angle{\rm BAC}\end{split}\)
これより、\(\angle{\rm ABF}=\angle{\rm BAF}\) となり、\(\triangle {\rm FAB}\) はこの２つの角を底角とする二等辺三角形となる [終]

---

\({\small (2)}~72^\circ\)

p.173 問5\(\begin{split}{\small (1)}~x=28^\circ\end{split}\)　　\(\begin{split}{\small (2)}~x=55^\circ\end{split}\)
\(\begin{split}{\small (3)}~x=34^\circ\end{split}\)

p.173 問6線分ＡＢが直径であるから、
\(\begin{split}~~~\angle{\rm ADB}=90^\circ\end{split}\)
したがって、\({\rm AD\perp BC}\)

p.173 問7三角定規で直角をとれば、直径が描ける
２本の直径を描くことで、その交点が円の中心となる

p.175 問1\(\begin{split}~~~\angle x=35^\circ\end{split}\)

p.175 問2[証明] 線分ＡＢが直径であるから、
\(\begin{split}~~~\angle{\rm ACB}=\angle{\rm ADB}=90^\circ\end{split}\)
よって、
\(\begin{split}~~~\angle{\rm FCE}=\angle{\rm FDE}=90^\circ\end{split}\)
したがって、４点Ｃ、Ｄ、Ｅ、Ｆについて、点Ｃ、Ｄが直線ＥＦと同じ側にあり、
\(\begin{split}~~~\angle{\rm FCE}=\angle{\rm FDE}\end{split}\)
であるから、
４点Ｃ、Ｄ、Ｅ、Ｆは同一円周上にある [終]

p.179 問1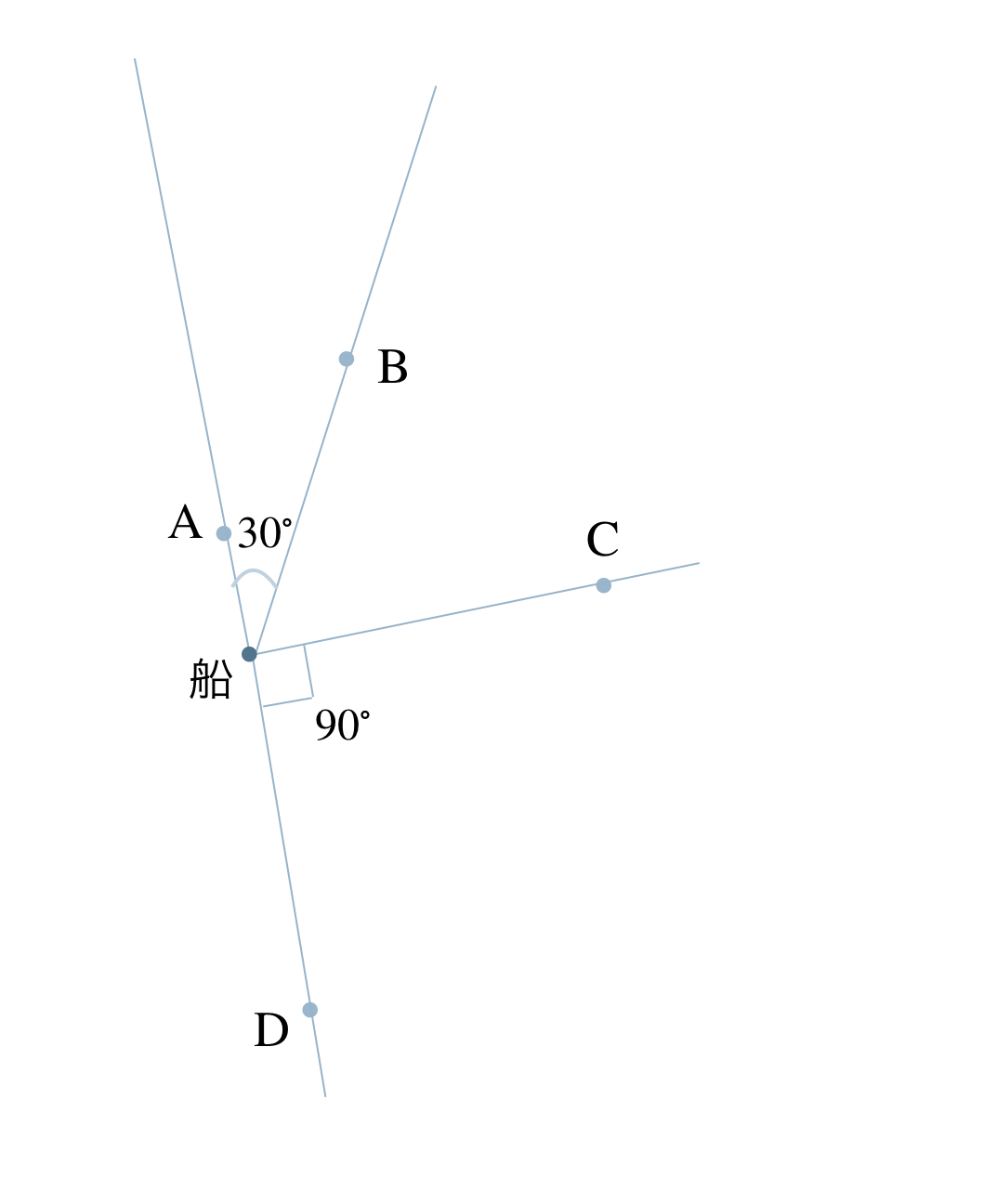
① \(30^\circ~,~60^\circ~,~90^\circ\) の三角定規を、\(30^\circ\) の角をはさむ２つの辺の上にＡ、Ｂがくるように置く
② \(45^\circ~,~45^\circ~,~90^\circ\) の三角定規を、\(90^\circ\) の角をはさむ２つの辺の上にＣ、Ｄがくるように置く
③ 辺上のＡ、Ｂ、Ｃ、Ｄがずれないように２つの三角定規をスライドさせて、\(30^\circ\) と \(90^\circ\) の頂点が重なる点が船の位置となる

p.181 問2\(\begin{split}~~~{\rm PD}=\frac{\,28\,}{\,5\,}=5.6~{\rm cm}\end{split}\)

p.181 問3[証明] \(\triangle {\rm ABP}\) と \(\triangle {\rm ADB}\) において、
等しい弧に対する円周角は等しいから、
\(\begin{split}~~~\angle{\rm ABP}=\angle{\rm ADB}~~~\cdots{\large ①}\end{split}\)
また、共通の角より、
\(\begin{split}~~~\angle{\rm PAB}=\angle{\rm BAD}~~~\cdots{\large ②}\end{split}\)
①、②より、２組の角がそれぞれ等しいから、
\(\begin{split}~~~\triangle {\rm ABP}∽\triangle {\rm ADB}\end{split}\)
[終]

p.181 問4\(\triangle {\rm ABC}\) と \(\triangle {\rm EDC}\) において、
ＢＣが直径であるから、
\(\begin{split}~~~\angle{\rm BAC}=\angle{\rm DEC}=90^\circ\end{split}\)
よって、
\(\begin{split}~~~\angle{\rm BAC}=\angle{\rm DEC}~~~\cdots{\large ①}\end{split}\)
また、\(\angle{\rm ABC}=60^\circ\) より、
\(\begin{split}~~~\angle{\rm ABD}=\angle{\rm DBC}=\angle{\rm ACB}=30^\circ\end{split}\)
次に、\(\overset{\frown}{\rm AE}\) に対する円周角が等しいから、
\(\begin{split}~~~\angle{\rm ABE}=\angle{\rm ACE}\end{split}\)
よって、
\(\begin{split}~~~\angle{\rm ACB}=\angle{\rm ECD}=30^\circ~~~\cdots{\large ②}\end{split}\)
①、②より、２組の角がそれぞれ等しいから、
\(\begin{split}~~~\triangle {\rm ABC}∽\triangle {\rm EDC}\end{split}\)
[終]