【ご注意ください】このページの内容について
このページは、旧版教科書に基づいて作成された内容です。
現在の教科書とは一部内容や表現が異なる場合があります。
順次、最新版に対応したページへと更新を進めておりますので、ご了承ください。
3章 1次関数

文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
学校図書中2 1章 式の計算(令和7年度対応)
学校図書中2 2章 連立方程式(令和7年度対応)
学校図書中2 3章 1次関数
学校図書中2 4章 図形の性質の調べ方
学校図書中2 5章 三角形・四角形
学校図書中2 6章 確率
学校図書中2 7章 データの分析
3章 1次関数
1 1次関数
» 1次関数の式
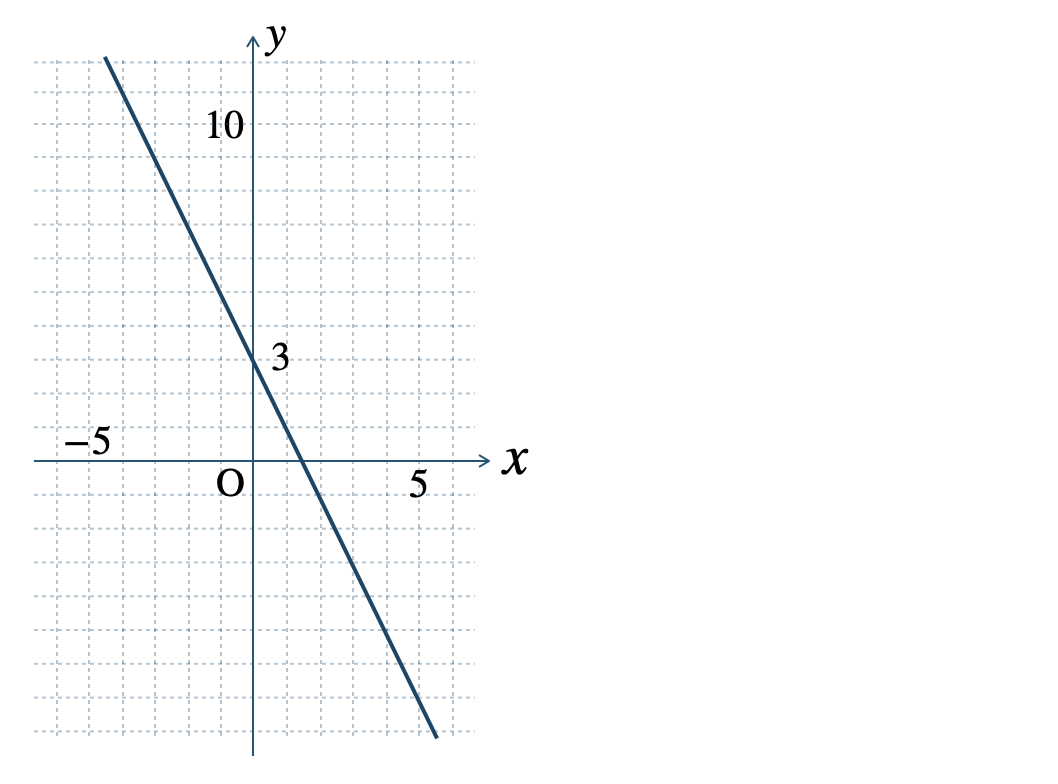
\(\begin{split}{\small (1)}~0.5~{\rm cm}\end{split}\) \(\begin{split}{\small (2)}~y=-\frac{\,1\,}{\,2\,}x+14\end{split}\)
\(\begin{split}{\small (3)}~\end{split}\)いえる
» 1次関数の式
\(\begin{split}{\small (2)}~y=\frac{\,28\,}{\,x\,}\end{split}\)、いえない
\(\begin{split}{\small (3)}~y=0.8x\end{split}\)、いえる
\(\begin{split}{\small (4)}~y=\pi x^2\end{split}\)、いえない
» 1次関数の式
» 1次関数の変化の割合
一定で、\(x\) の係数と等しい
» 1次関数の変化の割合
一定で、\(x\) の係数と等しい
» 1次関数の変化の割合
\(\begin{split}y=-\frac{\,1\,}{\,2\,}x+14\end{split}\) の変化の割合は \(\begin{split}-\frac{\,1\,}{\,2\,}\end{split}\) で、1分間での線香の長さの変化量
» 1次関数の変化の割合
» 1次関数のグラフと切片
\(\begin{split}{\small (2)}~\end{split}\)
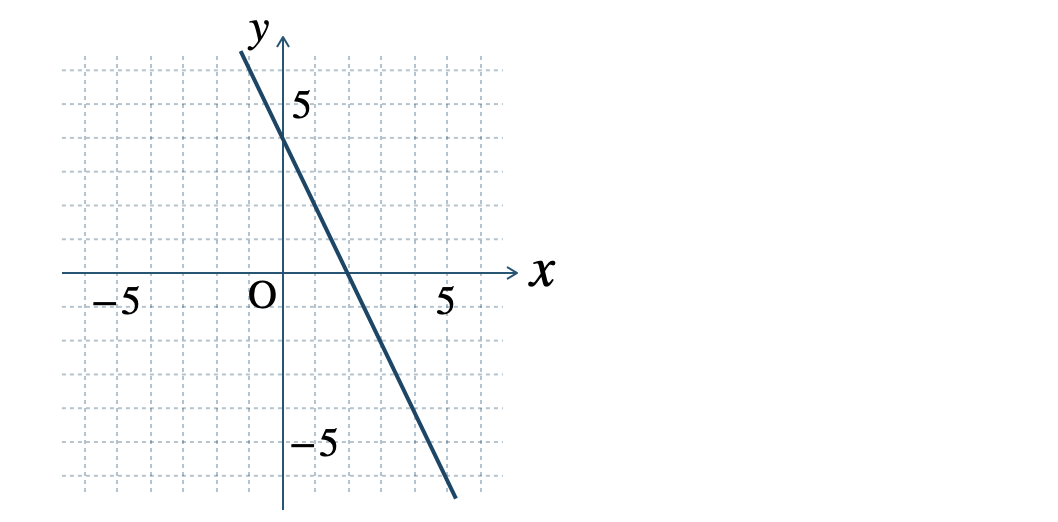
» 1次関数のグラフと切片
\(\begin{split}{\small (1)}~\frac{\,1\,}{\,2\,}\end{split}\) \(\begin{split}{\small (2)}~-2\end{split}\)
» 1次関数のグラフと傾き
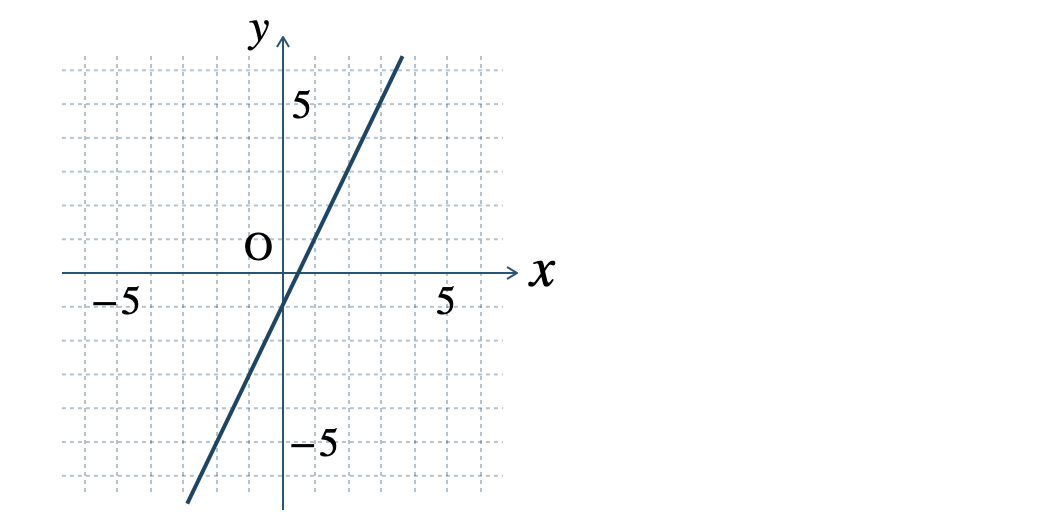
\(\begin{split}{\small (2)}~y=-x+3\end{split}\)
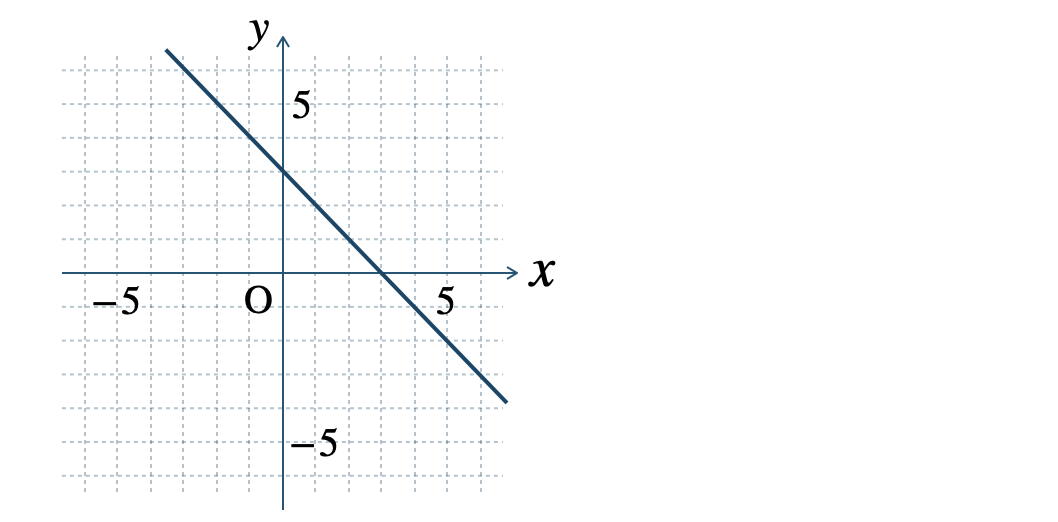
\(\begin{split}{\small (3)}~y=\frac{\,1\,}{\,3\,}x+2\end{split}\)
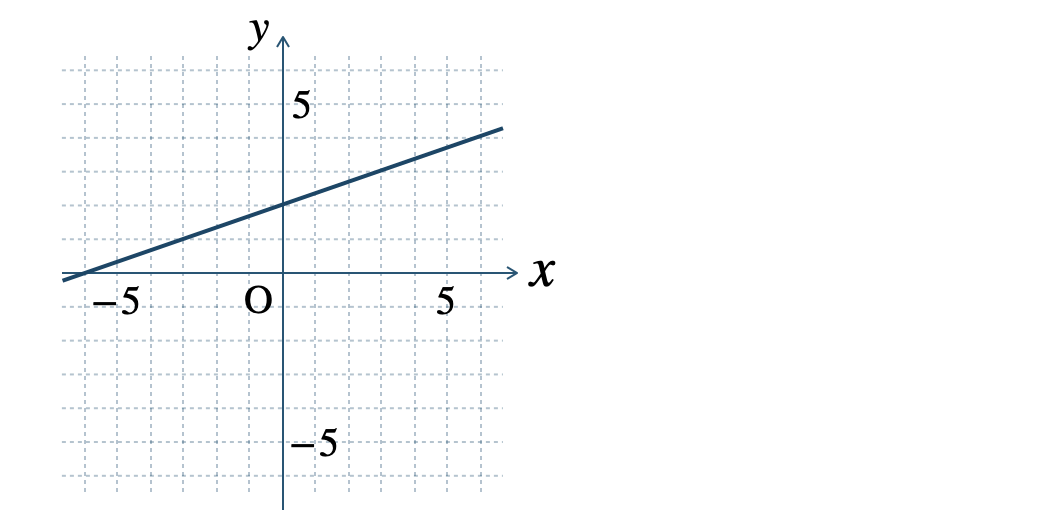
\(\begin{split}{\small (4)}~y=-\frac{\,3\,}{\,4\,}x-2\end{split}\)
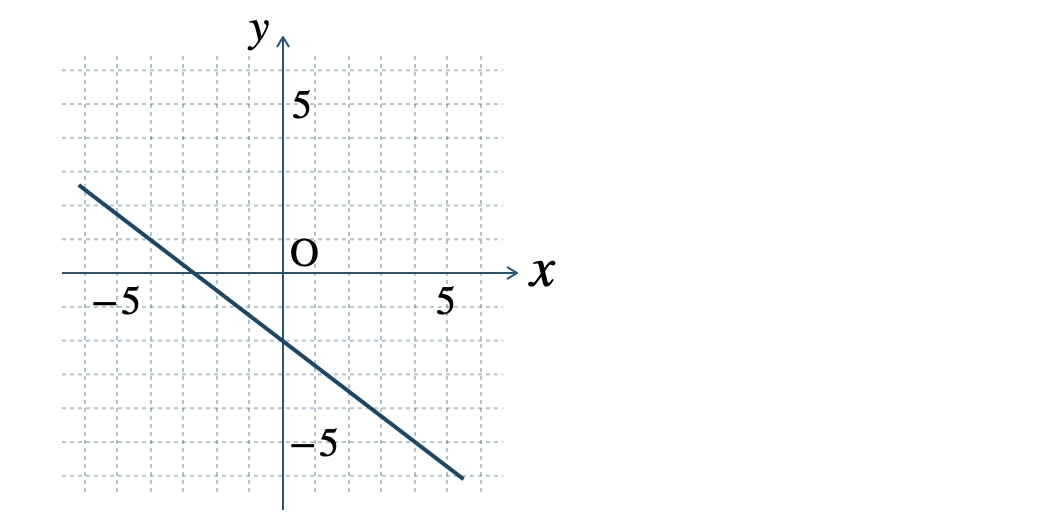
» 1次関数のグラフのかき方
\(\begin{split}y=\frac{\,3\,}{\,5\,}x+331\end{split}\)
秒速 \(341.8~{\rm m}\)
» グラフから1次関数の式を求める
① \(\begin{split}y=x+3\end{split}\) ② \(\begin{split}y=-\frac{\,3\,}{\,2\,}x+3\end{split}\)
③ \(\begin{split}y=-\frac{\,2\,}{\,3\,}x-2\end{split}\) ④ \(\begin{split}y=\frac{\,1\,}{\,2\,}x-2\end{split}\)
» グラフから1次関数の式を求める
\(\begin{split}{\small (1)}~y=3x-2\end{split}\) \(\begin{split}{\small (2)}~y=-\frac{\,2\,}{\,3\,}x+\frac{\,4\,}{\,3\,}\end{split}\)
\(\begin{split}{\small (3)}~y=x+2\end{split}\)
» 1次関数の式と条件
\(\begin{split}a=\frac{\,1\,}{\,2\,}~,~b=3\end{split}\) より、
\(\begin{split}y=\frac{\,1\,}{\,2\,}x+3\end{split}\)
» 2点を通る直線の式
\(\begin{split}{\small (3)}~y=-\frac{\,1\,}{\,2\,}x+3\end{split}\) \(\begin{split}{\small (4)}~y=2x-2\end{split}\)
» 2点を通る直線の式
\(\begin{split}y=-\frac{\,1\,}{\,3\,}x+\frac{\,2\,}{\,3\,}\end{split}\)
» 2点を通る直線の式
確かめよう
\(\begin{split}{\small (2)}~y=\frac{\,2\,}{\,5\,}x+30\end{split}\)
» 1次関数の式
\(\begin{split}{\small (1)}~\frac{\,1\,}{\,2\,}\end{split}\) \(\begin{split}{\small (2)}~3\end{split}\)
\(\begin{split}{\small (3)}~\end{split}\)
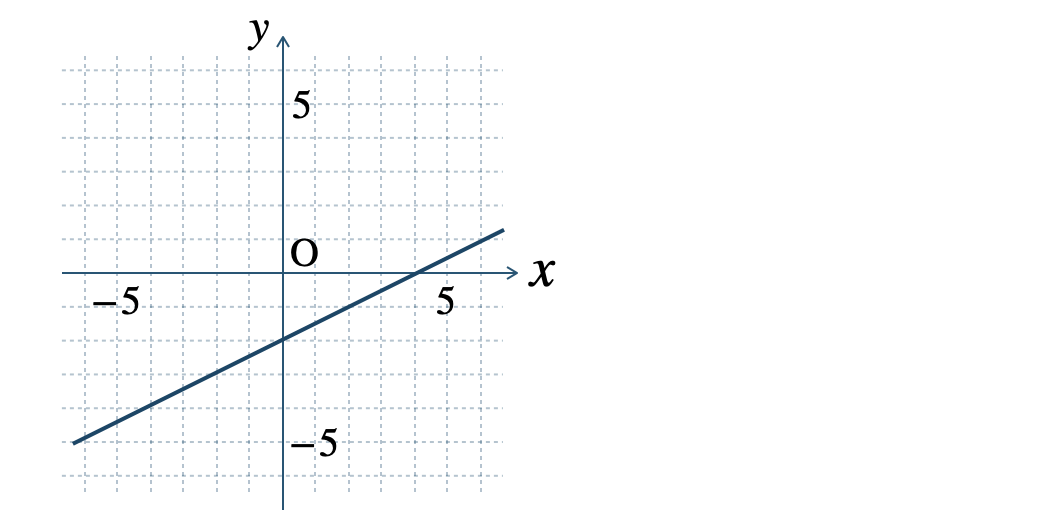
» 1次関数の変化の割合
» 1次関数のグラフのかき方
\(\begin{split}{\small (1)}~y=-\frac{\,2\,}{\,3\,}x+3\end{split}\) \(\begin{split}{\small (2)}~y=3x+3\end{split}\)
\(\begin{split}{\small (3)}~y=-x+2\end{split}\)
» グラフから1次関数の式を求める
» 1次関数の式と条件
» 2点を通る直線の式
2 方程式と1次関数
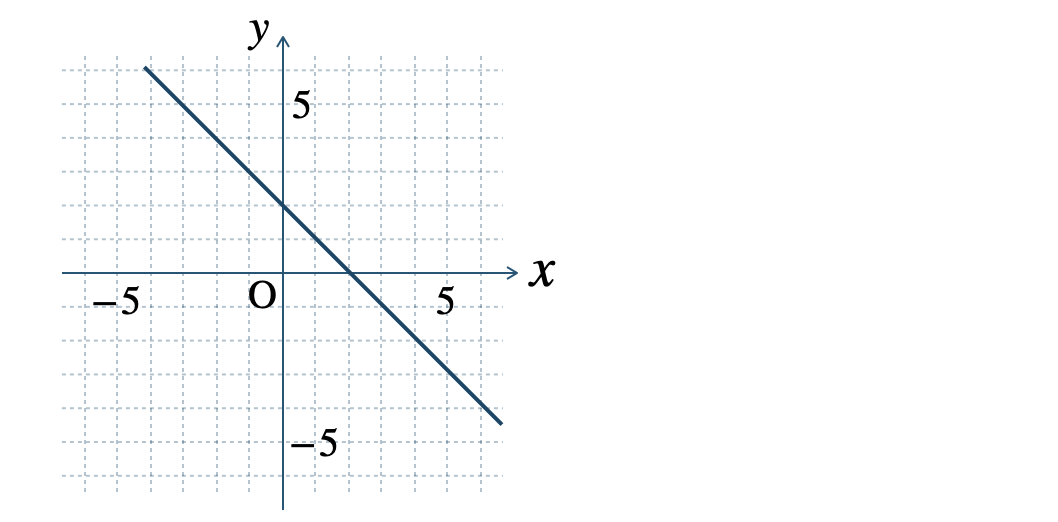
\(\begin{split}{\small (2)}~y=\frac{\,3\,}{\,2\,}x-2\end{split}\)
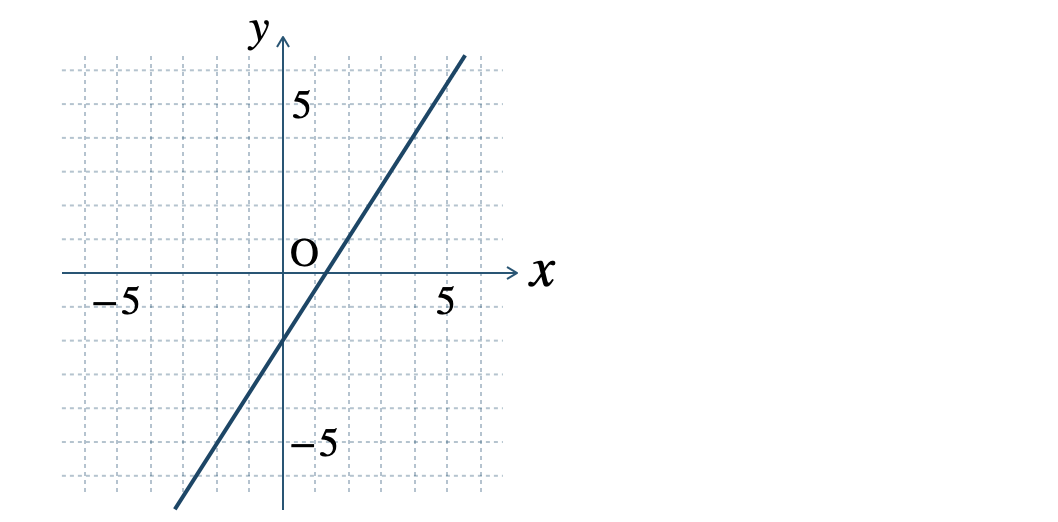
» 2元1次方程式のグラフ
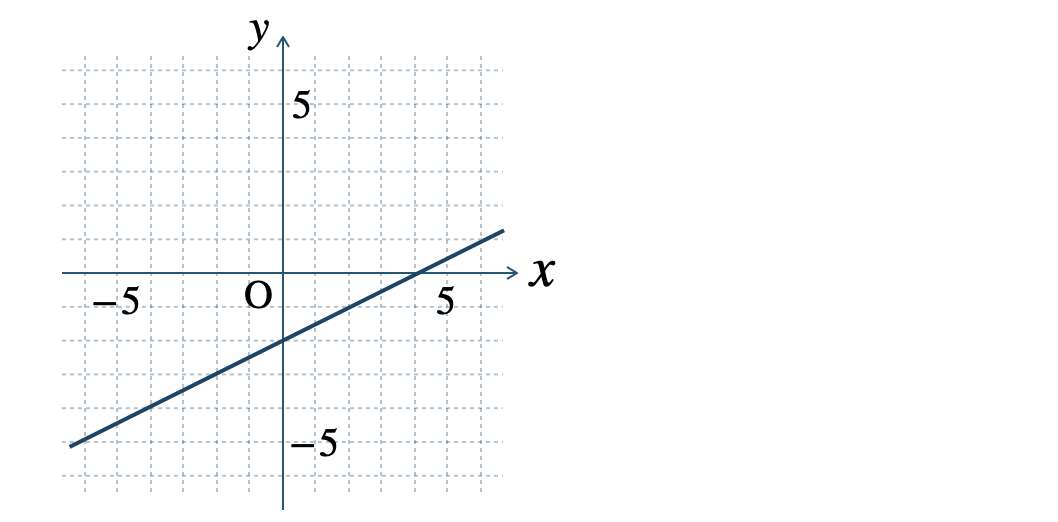
\(\begin{split}{\small (2)}~(0~,~4)~,~(3~,~0)\end{split}\)
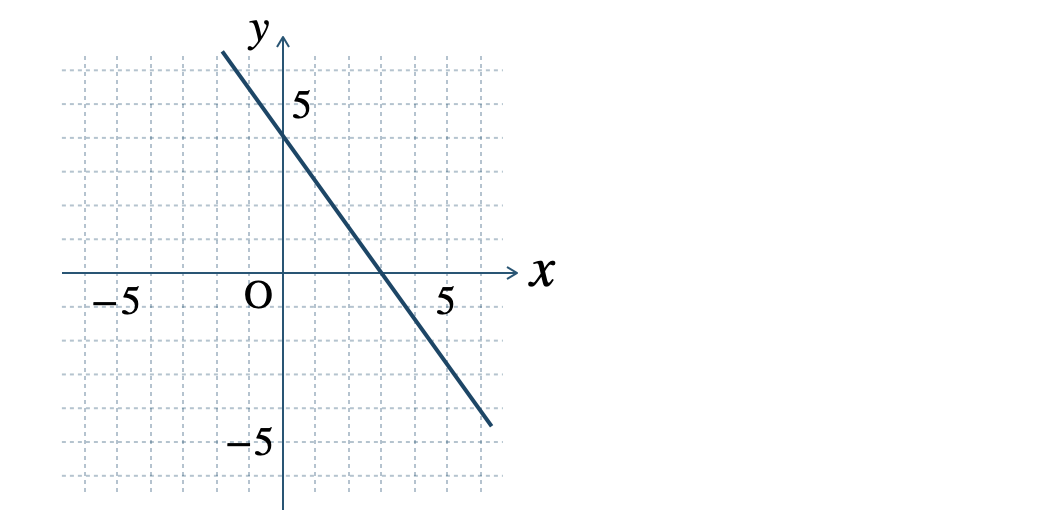
» 2元1次方程式のグラフ
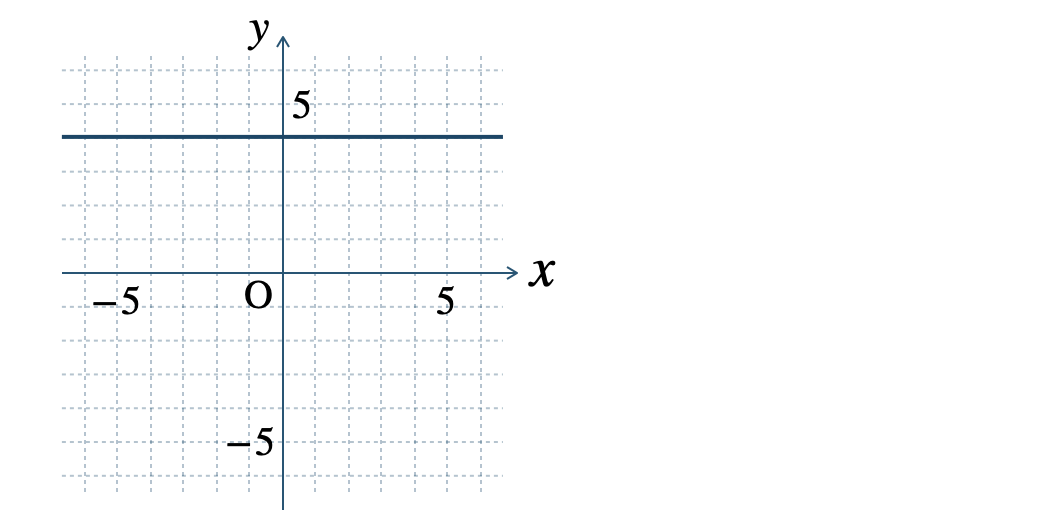
\(\begin{split}{\small (2)}~y=-2\end{split}\)
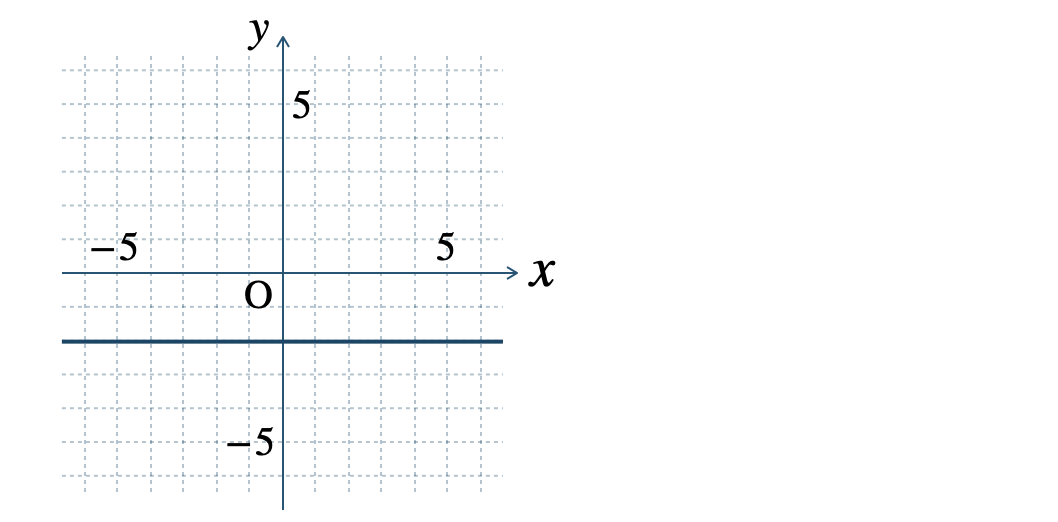
\(\begin{split}{\small (3)}~x=-3\end{split}\)
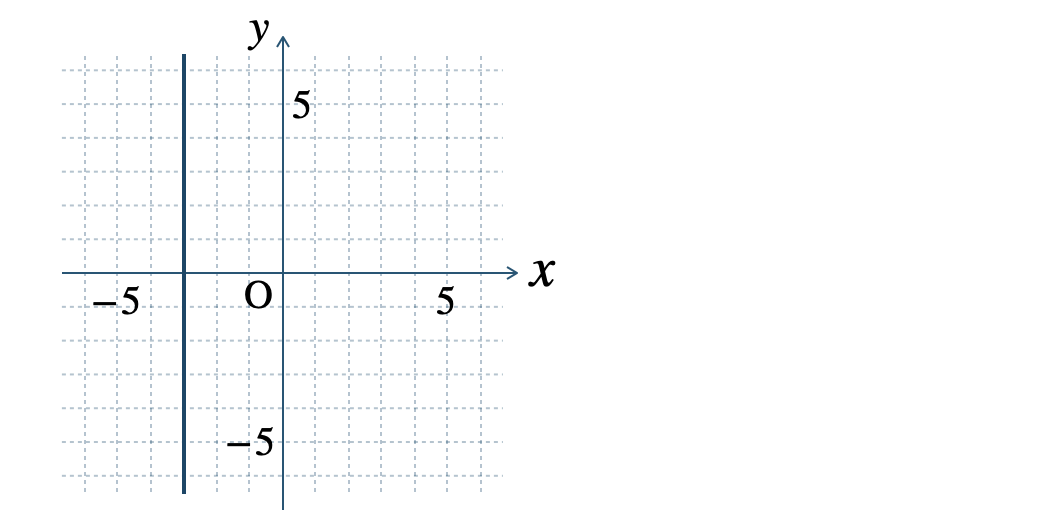
\(\begin{split}{\small (4)}~x=5\end{split}\)
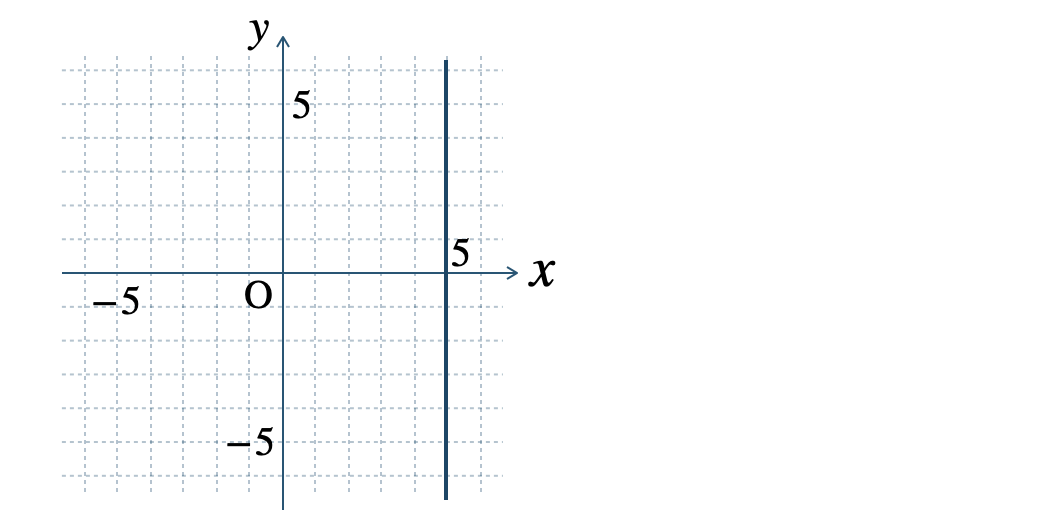
» 2元1次方程式のグラフ
» 連立方程式とグラフ
\(\begin{split}l\,:\,y=\frac{\,1\,}{\,2\,}x+2\end{split}\)
\(\begin{split}m\,:\,y=-x+5\end{split}\)
② \(x=2~,~y=3\)
よって、\({\rm P}(2~,~3)\)
» 連立方程式とグラフ
確かめよう
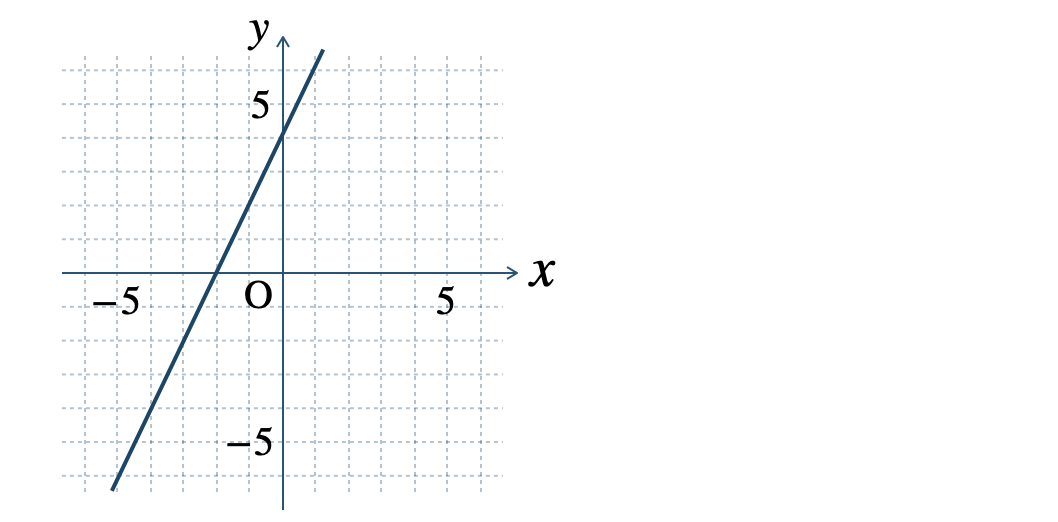
\(\begin{split}{\small (2)}~y=\frac{\,3\,}{\,5\,}x-3\end{split}\)
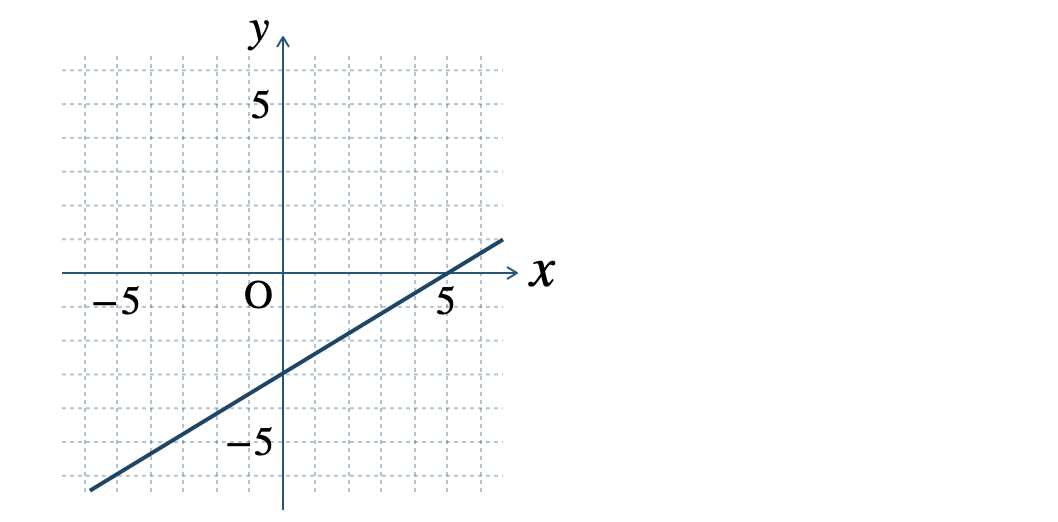
\(\begin{split}{\small (3)}~y=-3\end{split}\)
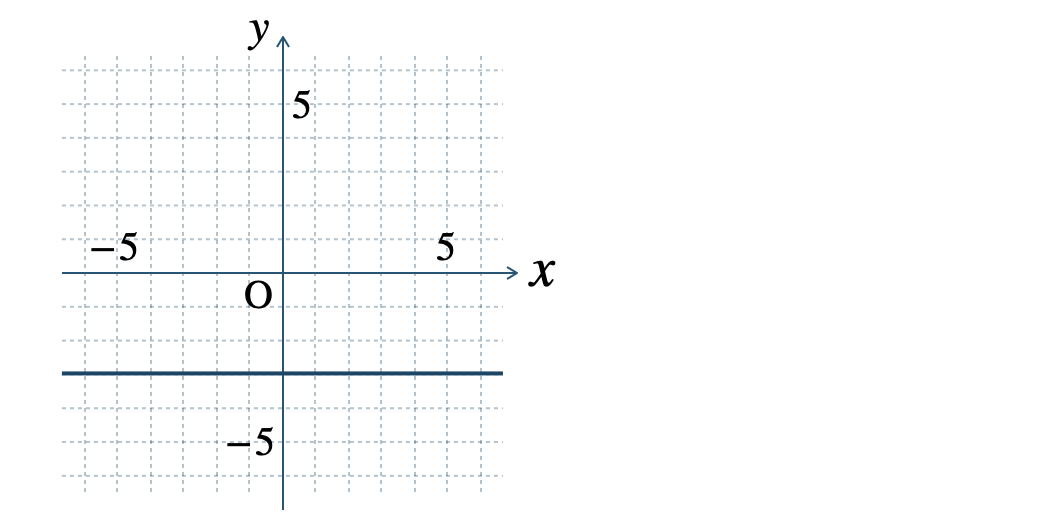
\(\begin{split}{\small (4)}~x=4\end{split}\)
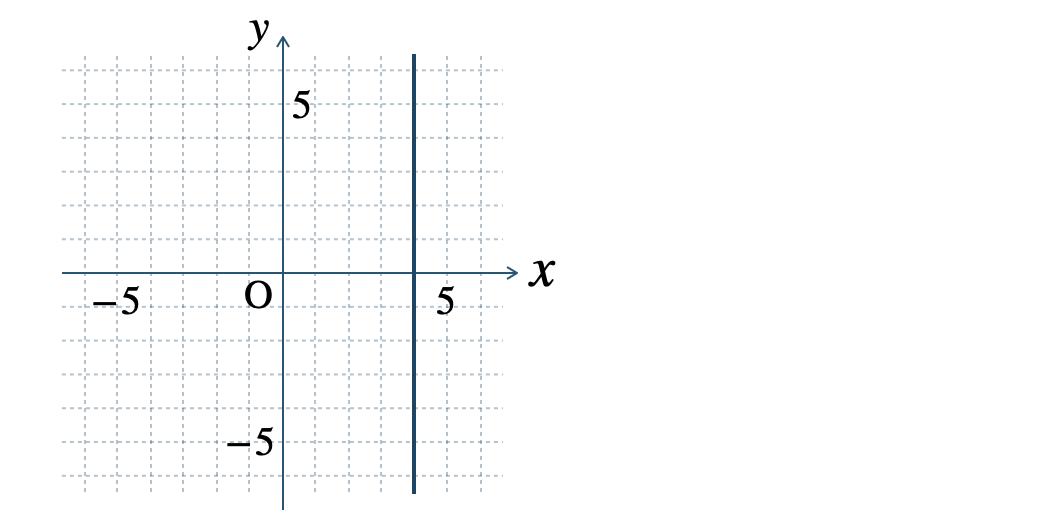
» 2元1次方程式のグラフ
\(\begin{split}l\,:\,y=\frac{\,3\,}{\,2\,}x+3\end{split}\)
\(\begin{split}m\,:\,y=-\frac{\,1\,}{\,2\,}x+1\end{split}\)
\(\begin{split}{\small (2)}~{\rm P}\left( -1 ~,~ \frac{\,3\,}{\,2\,} \right)\end{split}\)
» 連立方程式とグラフ
3 1次関数の利用
\(y>0\) でなければならないので、\(x<6\) となる
また、\(x≦3\) のときは、三角形がつくれないので、\(x>3\)
よって、\(x\) の変域は \(3<x<6\)
» 1次関数と動く点
陸さん、分速 \(180~{\rm m}\)
\(\begin{split}{\small (2)}~600~{\rm m}\end{split}\)
\(\begin{split}{\small (3)}~7.5\end{split}\) 分後、\(450~{\rm m}\)
\(\begin{split}{\small (4)}~\end{split}\)

» 1次関数と道のり
確かめよう

\(\begin{split}{\small (2)}~y=0.5x+25\end{split}\)
\(\begin{split}{\small (3)}~\end{split}\)約 \(34\) 分後
\(\begin{split}{\small (2)}~\end{split}\)行きは分速 \(80~{\rm m}\)、帰りは分速 \(60~{\rm m}\)
» 1次関数と道のり
次のページ「4章 図形の性質の調べ方」