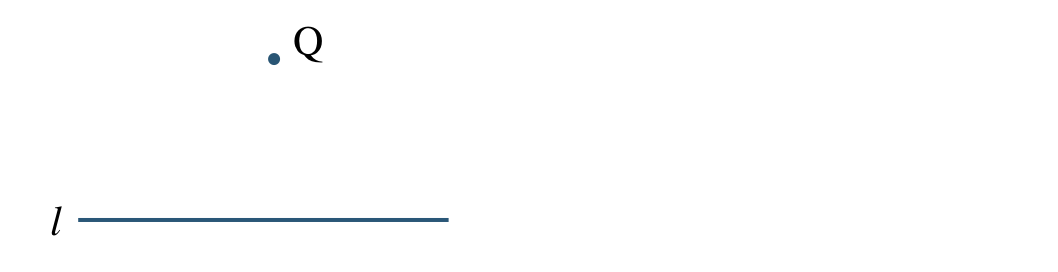このページは「中学数学1 平面図形」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう!
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
【問題一覧】中学数学1 平面図形
平面上の図形の表し方
\({\small (1)}~\)2点 \({\rm A~,~B}\) について、次のものを図で表せ。
① 直線 \({\rm AB}\) ② 線分 \({\rm AB}\)
③ 半直線 \({\rm AB}\) ④ 半直線 \({\rm BA}\)
\({\small (2)}~\)次の問いに答えよ。
① 2点 \({\rm A~,~B}\) 間の距離を記号で表せ。
② 2つの線分 \({\rm AB~,~CD}\) の長さが等しいことを記号で表せ。
\({\small (3)}~\)次の問いに答えよ。
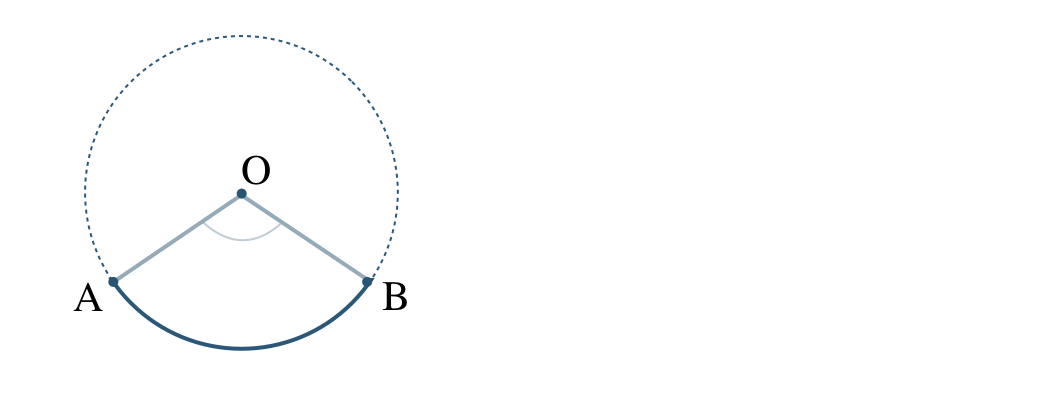
① 図のような角を3つの表し方で表せ。
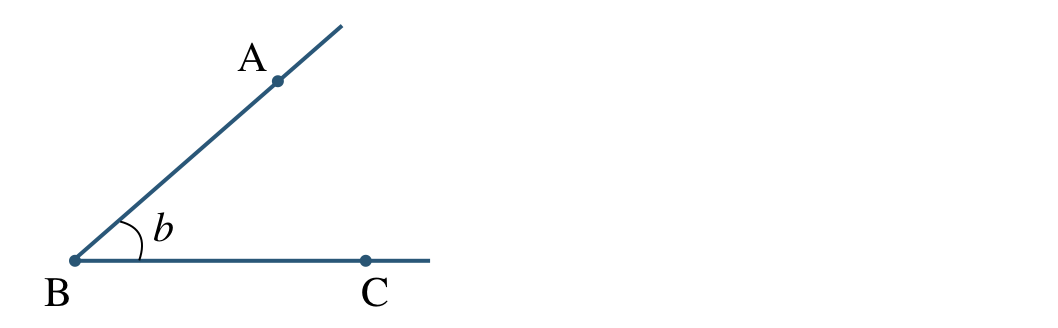
② 角 \({\rm A}\) と角 \({\rm B}\) の大きさが等しいことを記号で表せ。
③ 3点 \({\rm A~,~B~,~C}\) を頂点とする三角形を記号で表せ。
\({\small (4)}~\)次の問いに答えよ。
① 2直線 \({\rm AB~,~CD}\) が垂直に交わることを記号で表せ。また、このとき一方の直線を他の直線の何というか答えよ。
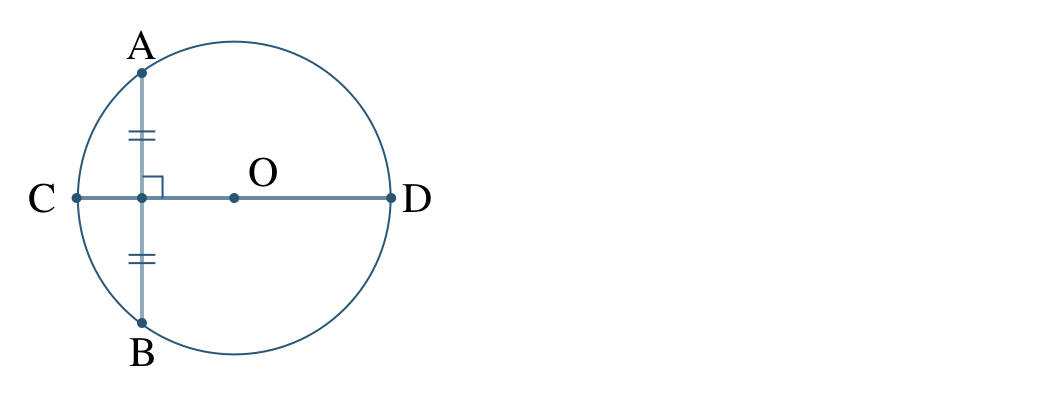
② 次の図で、点 \({\rm C}\) と直線 \({\rm AB}\) との距離をア〜ウから選べ。

③ 2直線 \({\rm AB~,~CD}\) が平行であることを記号で表せ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
①

②

③

④

\({\small (2)}~\)
① \({\rm AB}\)
② \({\rm AB=CD}\)
\({\small (3)}~\)
① \(\angle{\rm ABC}~,~\angle{\rm B}~,~\angle b\)
② \(\angle{\rm A}=\angle{\rm B}\)
③ \(\triangle {\rm ABC}\)
\({\small (4)}~\)
① \({\rm AB\perp CD}\)
一方の直線を他の直線の垂線
② イ
③ \({\rm AB\,//\, CD}\)

図形の平行移動
図の \(\triangle {\rm ABC}\) と矢印 \({\rm PQ}\) について、次の問いに答えよ。
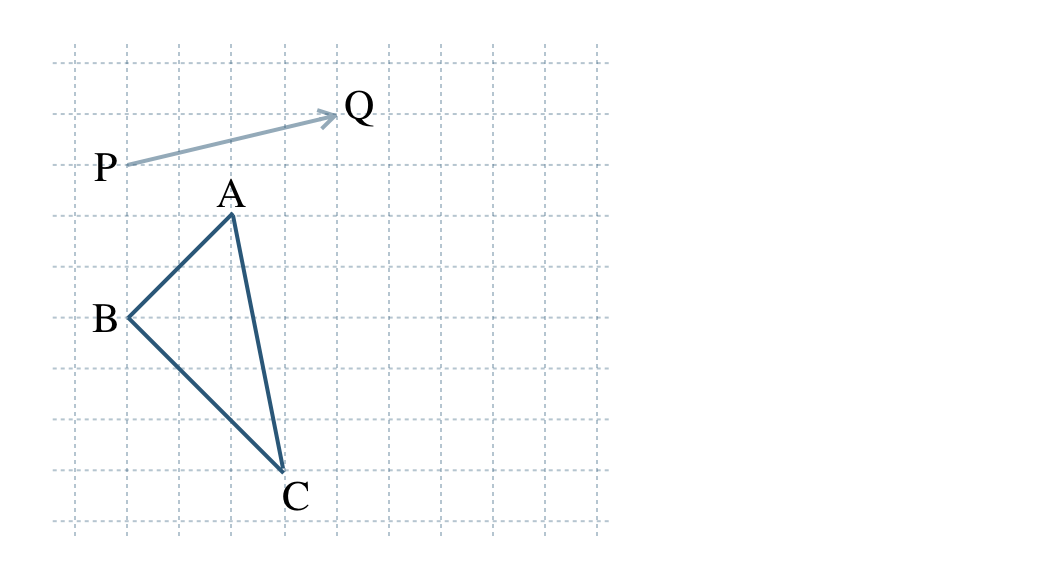
\({\small (1)}~\)\(\triangle {\rm ABC}\) を矢印 \({\rm PQ}\) の方向に線分 \({\rm PQ}\) の長さだけ平行移動させた \(\triangle {\rm A’B’C’}\) をかけ。
\({\small (2)}~\)\(\triangle {\rm ABC}\) と平行移動させた \(\triangle {\rm A’B’C’}\) について、3つの線分 \({\rm AA’~,~BB’~,~CC’}\) の関係を答えよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
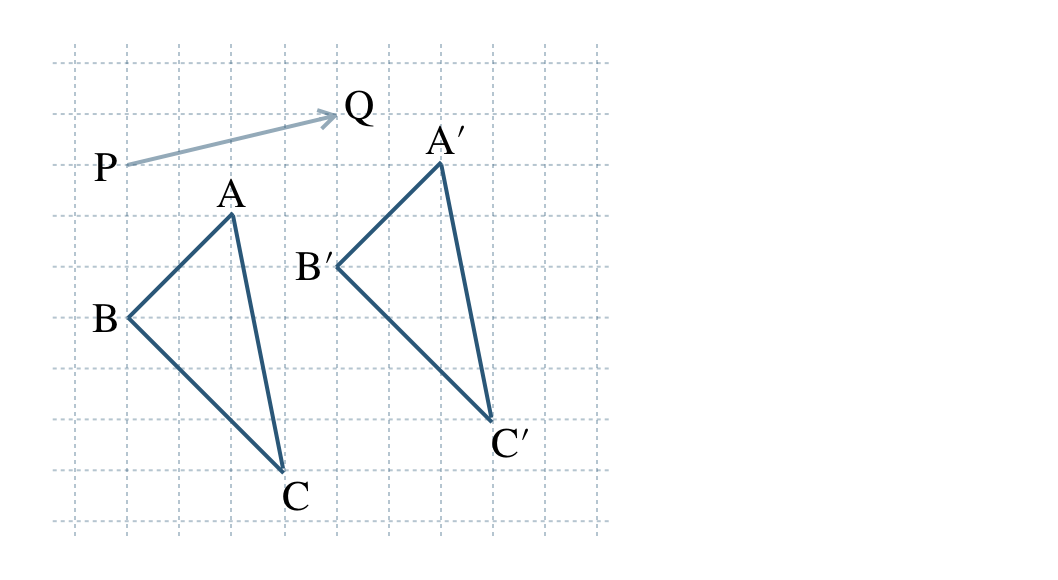
\({\small (2)}~\)どれも平行で長さが等しい
\({\rm AA’\,//\,BB’\,//\,CC’}\)
\({\rm AA’=BB’=CC’}\)

図形の回転移動
次の問いに答えよ。
\({\small (1)}~\)図の \(\triangle {\rm A’B’C’}\) は \(\triangle {\rm ABC}\) を点 \({\rm O}\) を中心として、反時計回りに \(90^\circ\) だけ回転移動させて図形である。

① 線分 \({\rm OA}\) と \({\rm OA’}\)、線分 \({\rm OB}\) と \({\rm OB’}\)、線分 \({\rm OC}\) と \({\rm OC’}\) の長さについて、どのような関係か答えよ。
② \(\angle {\rm AOA’}~,~\angle {\rm BOB’}~,~\angle {\rm COC’}\)の大きさをそれぞれ求めよ。
③ \(\angle {\rm AOB}\) と \(\angle {\rm A’OB’}\) はどのような関係であるか答えよ。
\({\small (2)}~\)次の図の \(\triangle {\rm A’B’C’}\) は \(\triangle {\rm ABC}\) に対して、どのような関係にあるか答えよ。
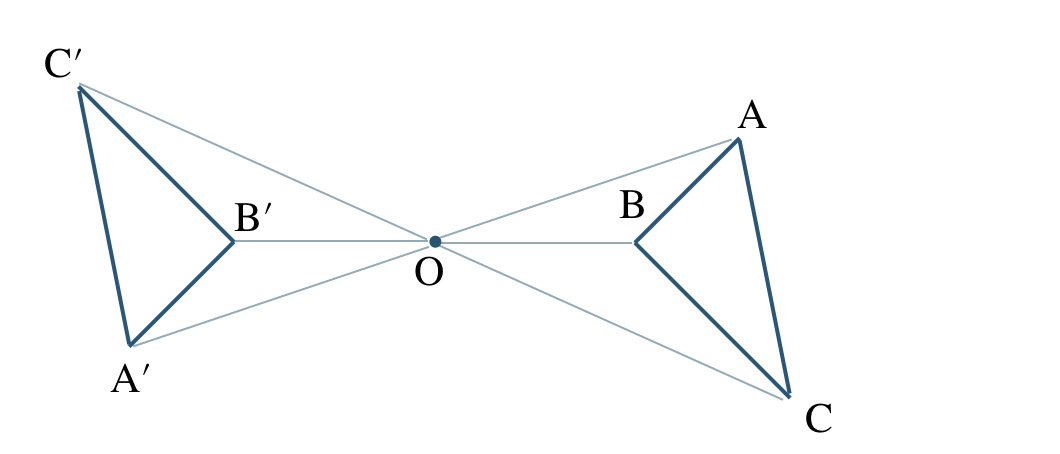
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(\begin{split}{\rm OA=OA’~,~OB=OB’~,~OC=OC’}\end{split}\)
② \(\begin{split}\angle {\rm AOA’}=\angle {\rm BOB’}=\angle {\rm COC’}=90^\circ\end{split}\)
③ \(\begin{split}\angle{\rm AOB}=\angle{\rm A’OB’}\end{split}\)
\({\small (2)}~\)点対称移動

図形の対称移動
\({\small (1)}~\)次の問いに答えよ。
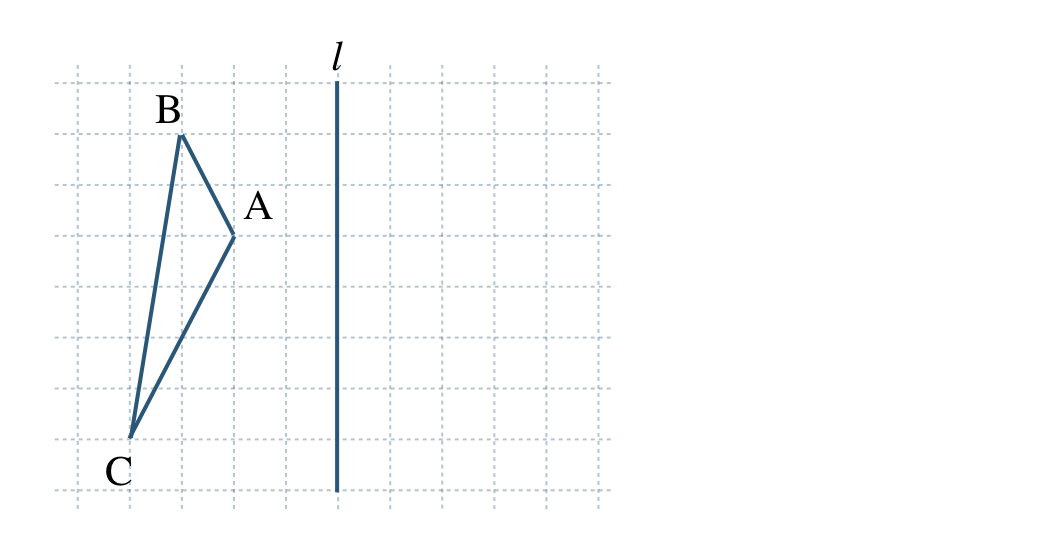
① \(\triangle {\rm ABC}\) を直線 \(l\) を対称の軸として対称移動させた \(\triangle {\rm A’B’C’}\) をかけ。
② 直線 \(l\) と線分 \({\rm AA’}\) の交点を何というか答えよ。また、線分 \({\rm AA’}\) に対して直線 \(l\) を何というか答えよ。
\({\small (2)}~\)次の図の、四角形 \({\rm ABCD}\) を線分 \({\rm AD}\) を対称の軸として対称移動させた図形をかけ。
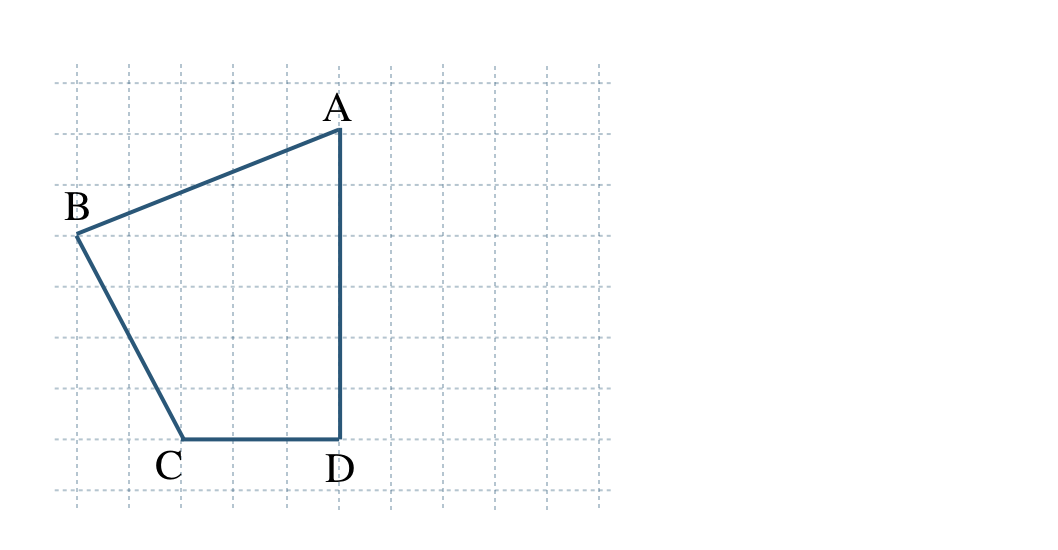
[ 解答を見る ]
【解答】
\({\small (1)}~\)
①
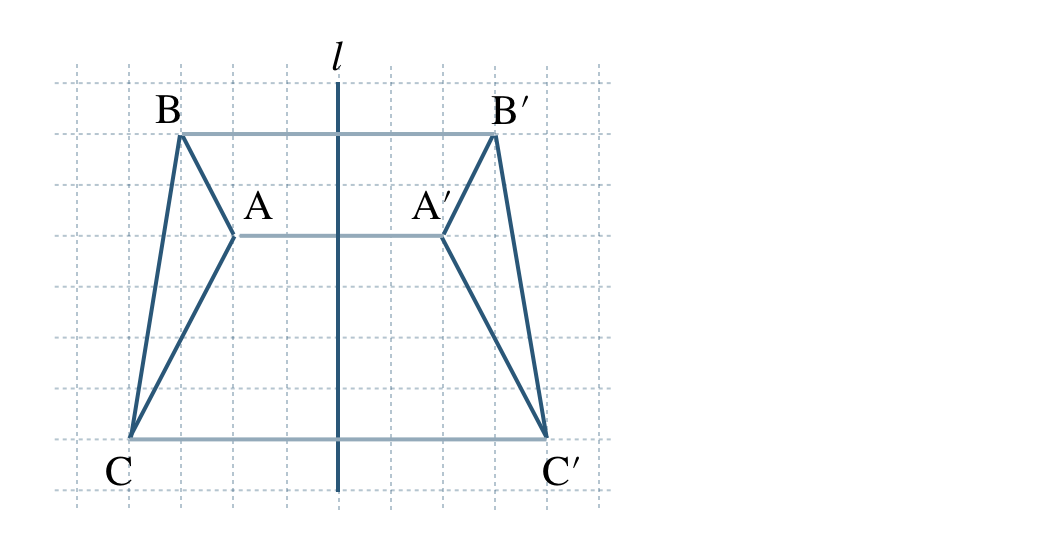
② 中点、垂直二等分線
\({\small (2)}~\)
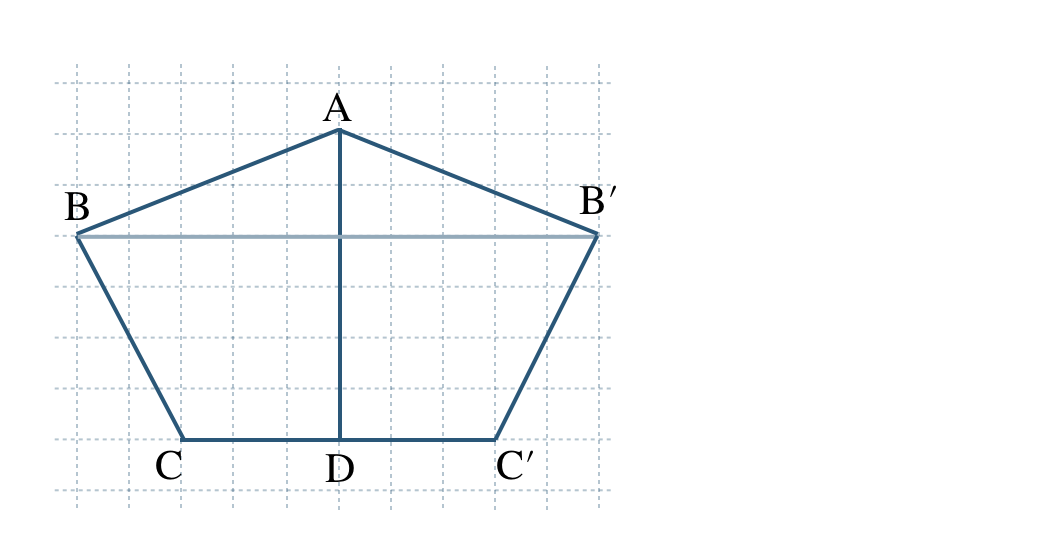

図形の移動のまとめ
正方形 \({\rm ABCD}\) を次の図のようにア〜クの8つの合同な直角二等辺三角形に分けた。
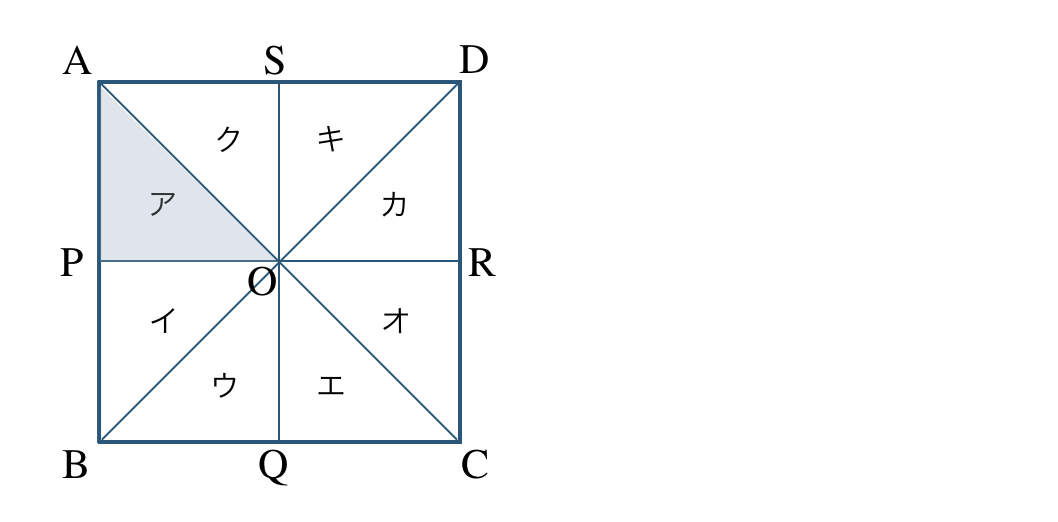
\({\small (1)}~\)次の条件の図形をア〜クから選べ。
① アを平行移動したときに重なる図形。
② アを平行移動したときに重なる図形。
\({\small (2)}~\)次の条件の図形をア〜クから選べ。
① アを線分 \({\rm PR}\) を対称の軸として、対称移動したときに重なる図形。
② アを線分 \({\rm SQ}\) を対称の軸として、対称移動したときに重なる図形。
③ アを線分 \({\rm AC}\) を対称の軸として、対称移動したときに重なる図形。
\({\small (3)}~\)次の条件の図形をア〜クから選べ。
① アを点 \({\rm O}\) を回転の中心として、時計回りに \(90^\circ\) 回転移動したときに重なる図形。
② アを点 \({\rm O}\) を回転の中心として、反時計回りに \(90^\circ\) 回転移動したときに重なる図形。
③ アを点 \({\rm O}\) を回転の中心として、点対称移動したときに重なる図形。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① エ ② キ
\({\small (2)}~\)
① イ ② カ ③ ク
\({\small (3)}~\)
① キ ② ウ ③ オ

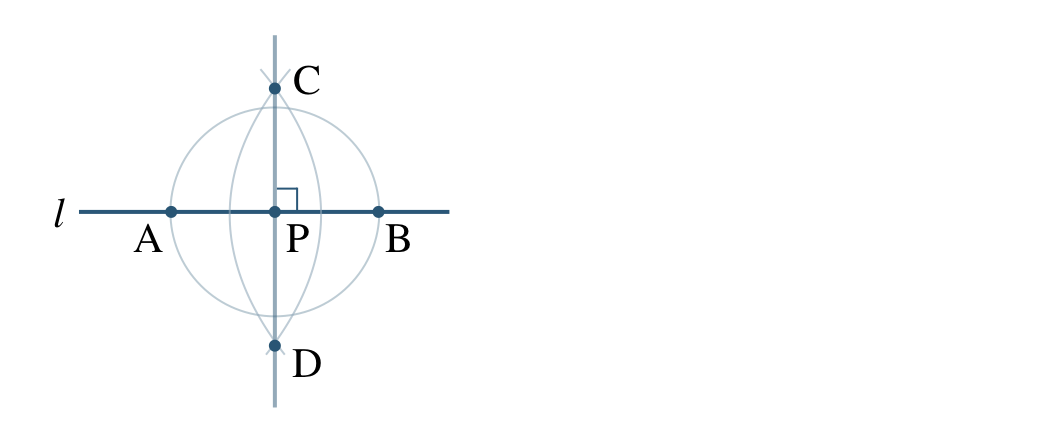
垂直二等分線の作図
次の問いに答えよ。
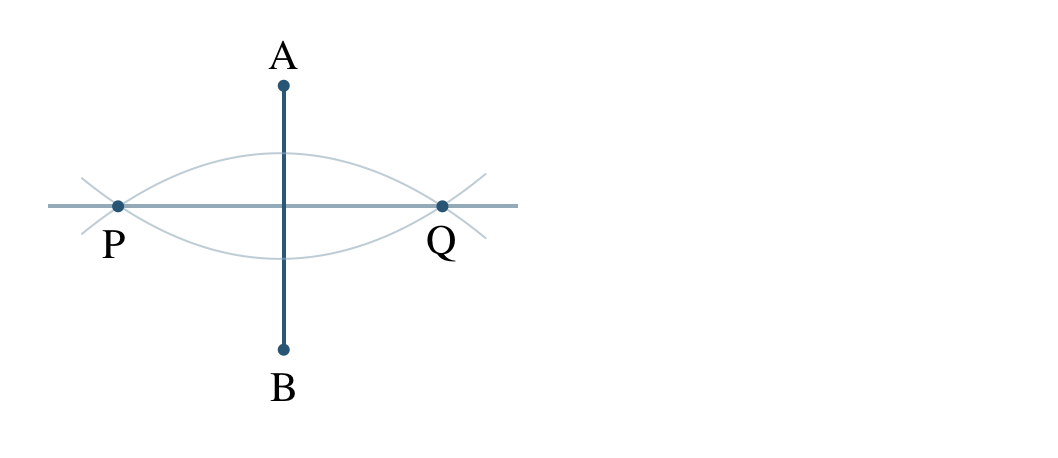
\({\small (1)}~\)次の線分 \({\rm AB}\) の垂直二等分線の作図をせよ。また、線分 \({\rm AB}\) の中点 \({\rm M}\) を作図せよ。

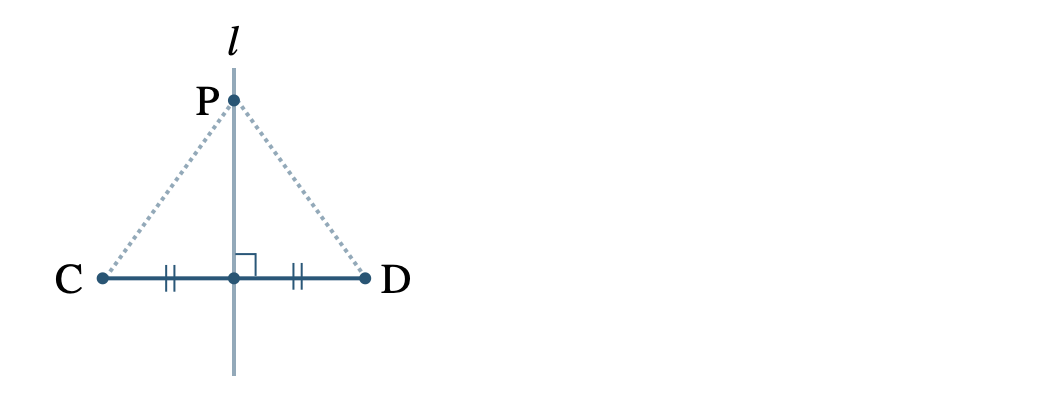
\({\small (2)}~\)次の図で、直線 \(l\) は線分 \({\rm CD}\) の垂直二等分線である。直線 \(l\) 上の点 \({\rm P}\) をとるとき、線分 \({\rm PC~,~PD}\) の関係を答えよ。
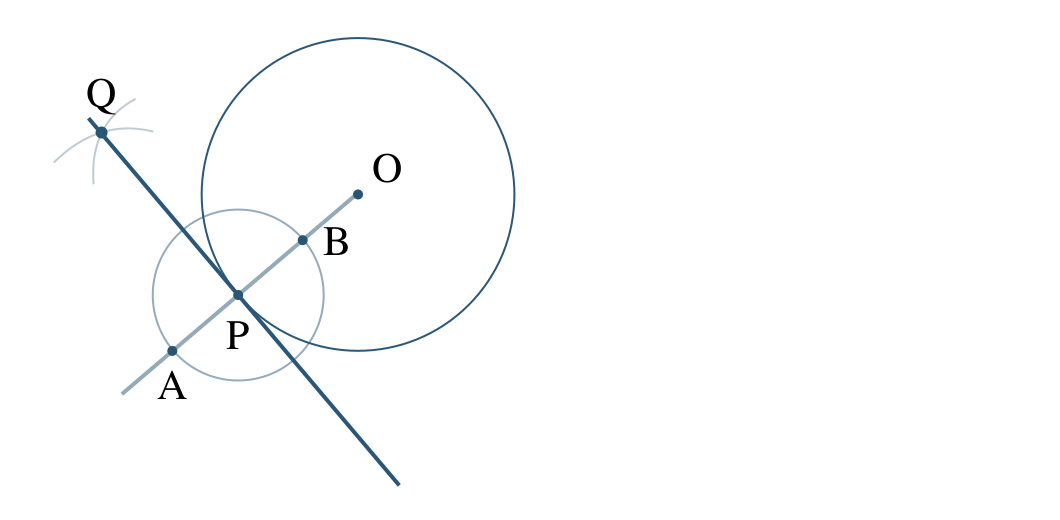
\({\small (3)}~\)次の図で、直線 \(m\) 上にあり、2点 \({\rm E~,~F}\) からの距離が等しい点 \({\rm R}\) の作図をせよ。

[ 解答を見る ]
【解答】
\({\small (1)}~\)

\({\small (2)}~{\rm PC=PD}\)
\({\small (3)}~\)


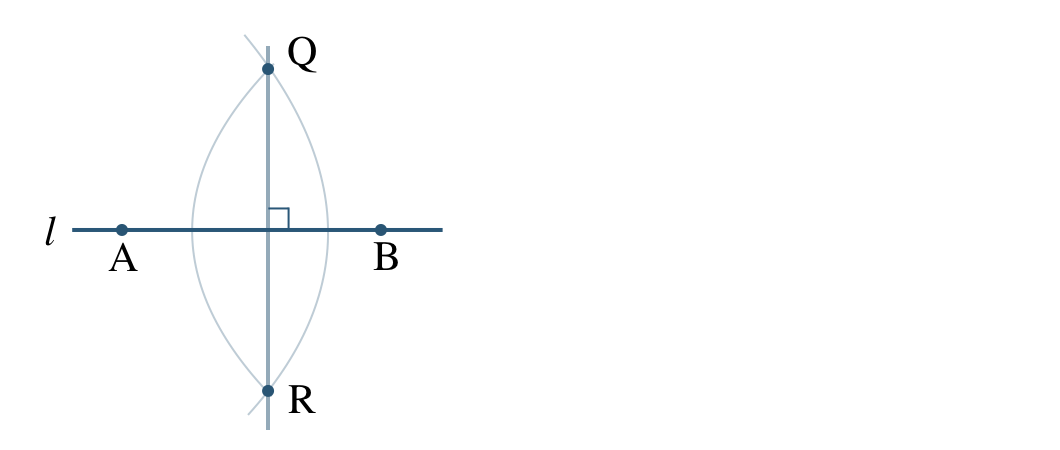
角の二等分線の作図
次の問いに答えよ。
\({\small (1)}~\angle{\rm AOB}\) の二等分線を作図せよ。
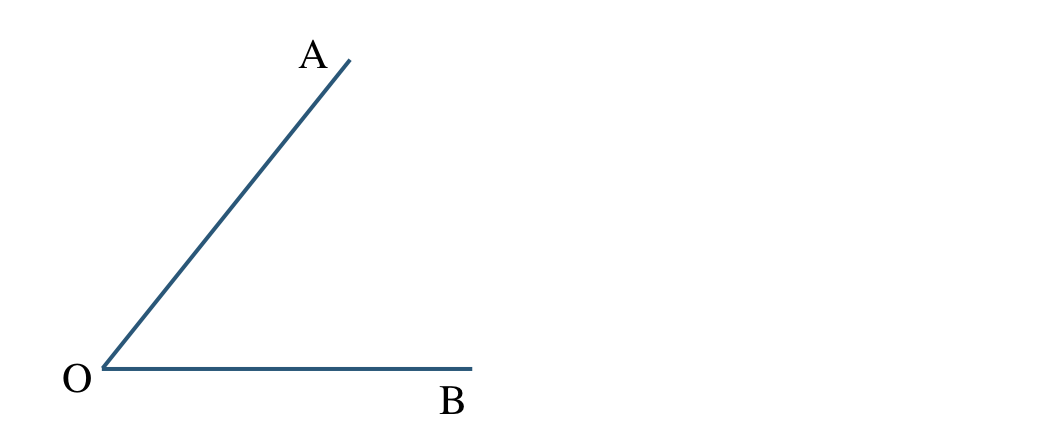
\({\small (2)}~\angle{\rm COD}\) の二等分線を作図せよ。

[ 解答を見る ]
【解答】
\({\small (1)}~\)
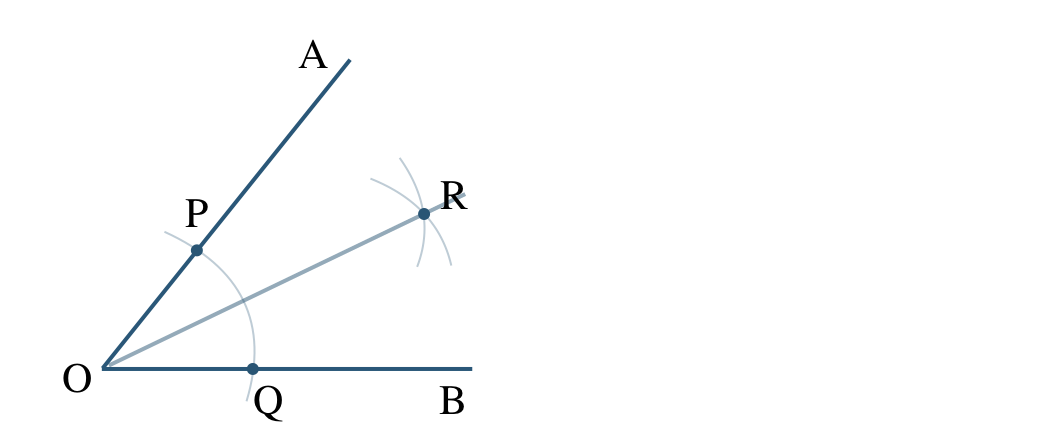
\({\small (2)}~\)
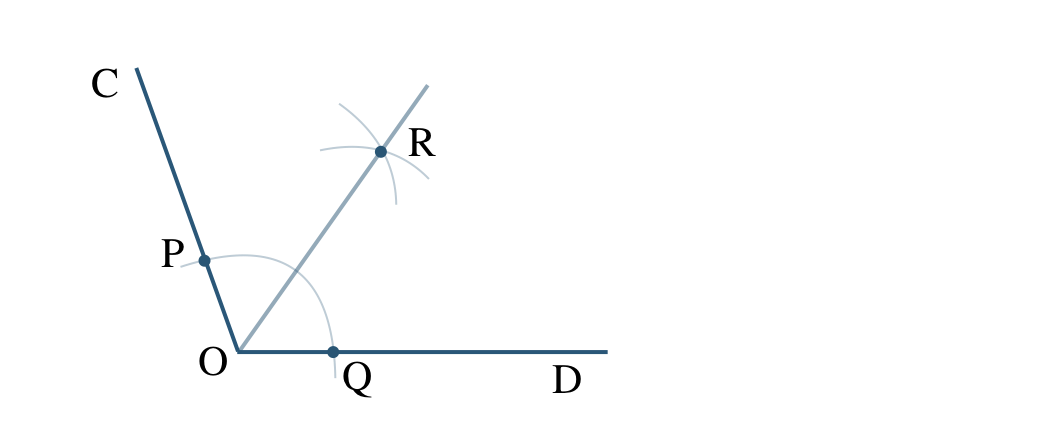

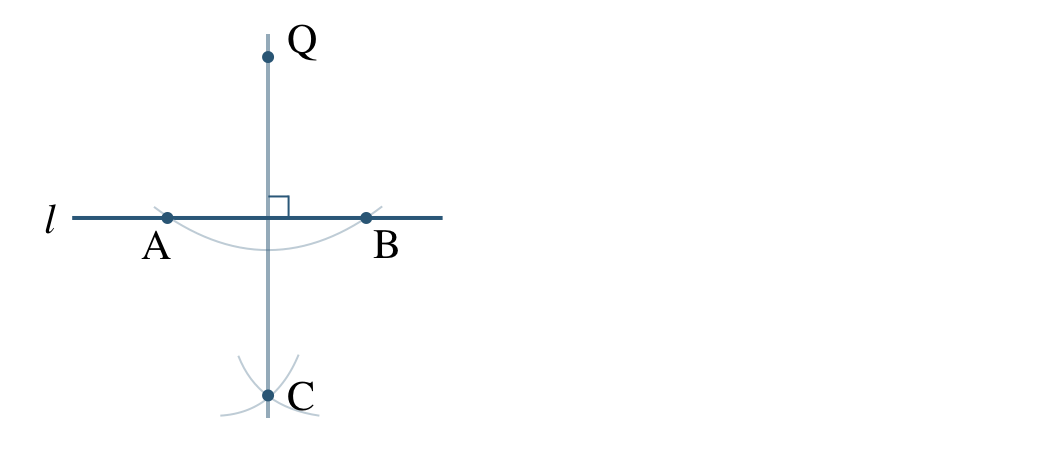
垂線の作図
次の問いに答えよ。
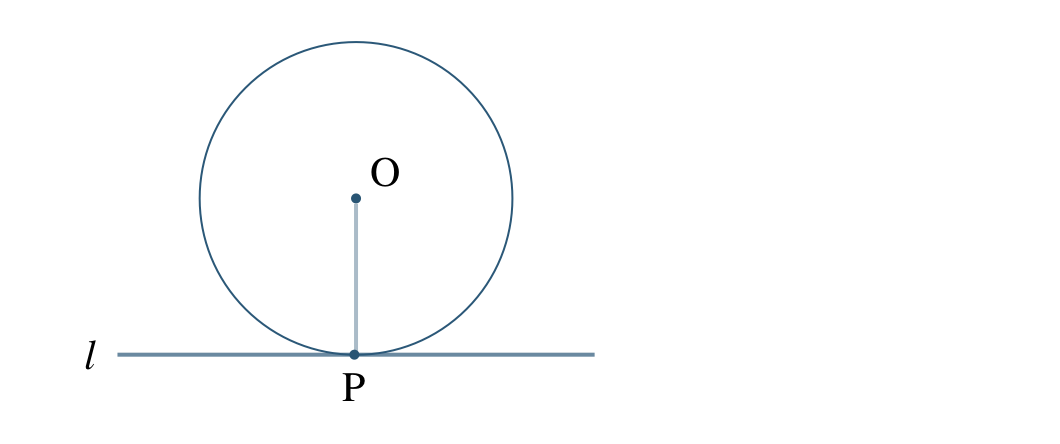
\({\small (1)}\)点 \({\rm P}\) を通る直線 \(l\) の垂線を作図せよ。
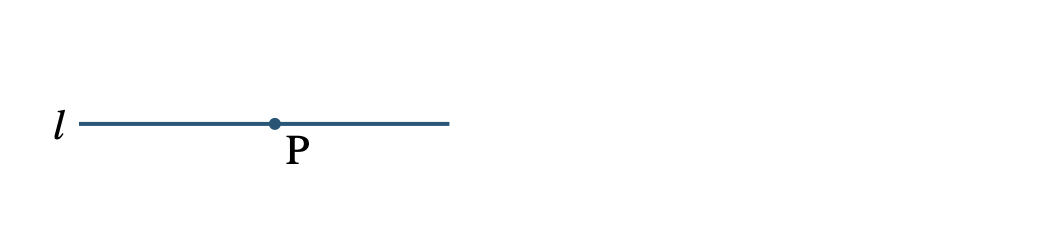
\({\small (2)}~\)点 \({\rm Q}\) を通る直線 \(l\) の垂線を作図せよ。