啓林館：未来へ広がる数学１

p.115 問1\(~~~\)ア、ウ

p.115 問2\(y\) の値は、
　\(196~,~144~,~100~,~64~,~36~,~16~,~4\)

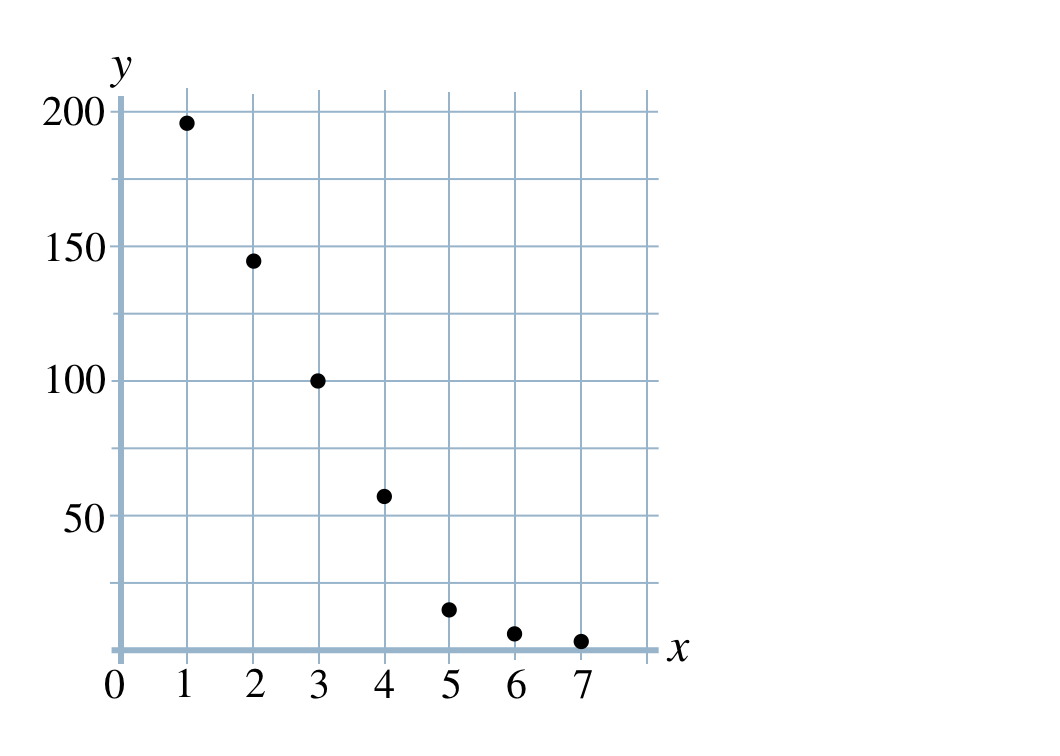
\(x\) の値を大きくすると、\(y\) の値は小さくなる

p.116 問3\(\begin{split}~~~y=-2x+16\end{split}\)

p.116 問4\(\begin{split}~~~3≦x < 10\end{split}\)

p.118 問1\({\small (1)}~\)\(y=120x\) となり、\(y\) は \(x\) に比例する
　また、比例定数は \(120\)

---

\({\small (2)}~\)\(y=4x\) となり、\(y\) は \(x\) に比例する
　また、比例定数は \(4\)

p.120 問2\(y\) の値は、
　\(8~,~6~,~4~,~2~,~0~,~\)
　\(-2~,~-4~,~-6~,~-8~,~\cdots\)

---

\(x\) の値が \(2\) 倍、\(3\) 倍、\(4\) 倍、…となると、
\(y\) の値が \(2\) 倍、\(3\) 倍、\(4\) 倍、…となる

---

\(x\) と \(y\) の値の商 \(\begin{split}\frac{\,y\,}{\,x\,}\end{split}\) は、

---

\(\begin{split}~~~\frac{\,8\,}{\,-4\,}=-2~,~\frac{\,6\,}{\,-3\,}=-2~,~\end{split}\)

---

\(\begin{split}~~~\frac{\,4\,}{\,-2\,}=-2~,~\frac{\,2\,}{\,-1\,}=-2~,~\cdots\end{split}\)

---

よって、一定で比例定数 \(-2\) と等しい

p.120 説明しよう(イ)が比例の関係
\(x\) と \(y\) の商 \(\begin{split}\frac{\,y\,}{\,x\,}\end{split}\) が

---

\(\begin{split}~~~\frac{\,12\,}{\,-4\,}=-3~,~\frac{\,9\,}{\,-3\,}=-3~,~\end{split}\)

---

\(\begin{split}~~~\frac{\,6\,}{\,-2\,}=-3~,~\frac{\,3\,}{\,-1\,}=-3\end{split}\)

---

よって、一定となるので \(x\) と \(y\) は比例している

p.120 問3\(\begin{split}{\small (1)}~y=4x\end{split}\)　　\(\begin{split}{\small (2)}~y=-10x\end{split}\)

p.121 練習問題 1

---

(ア) \(y=5x\)　　(ウ) \(\begin{split}y=\frac{1}{80}x\end{split}\)

p.123 問1

p.123 問2\(\begin{split}~~~{\rm F} (4~,~6)~,~{\rm G}(5~,~0)~,~{\rm H} (6~,~-2)\end{split}\)
\(\begin{split}~~~{\rm I}(0~,~-3)~,~{\rm G} (-6~,~0)\end{split}\)

p.124 問1

p.125 問2

p.126 問3\({\small (1)}~\)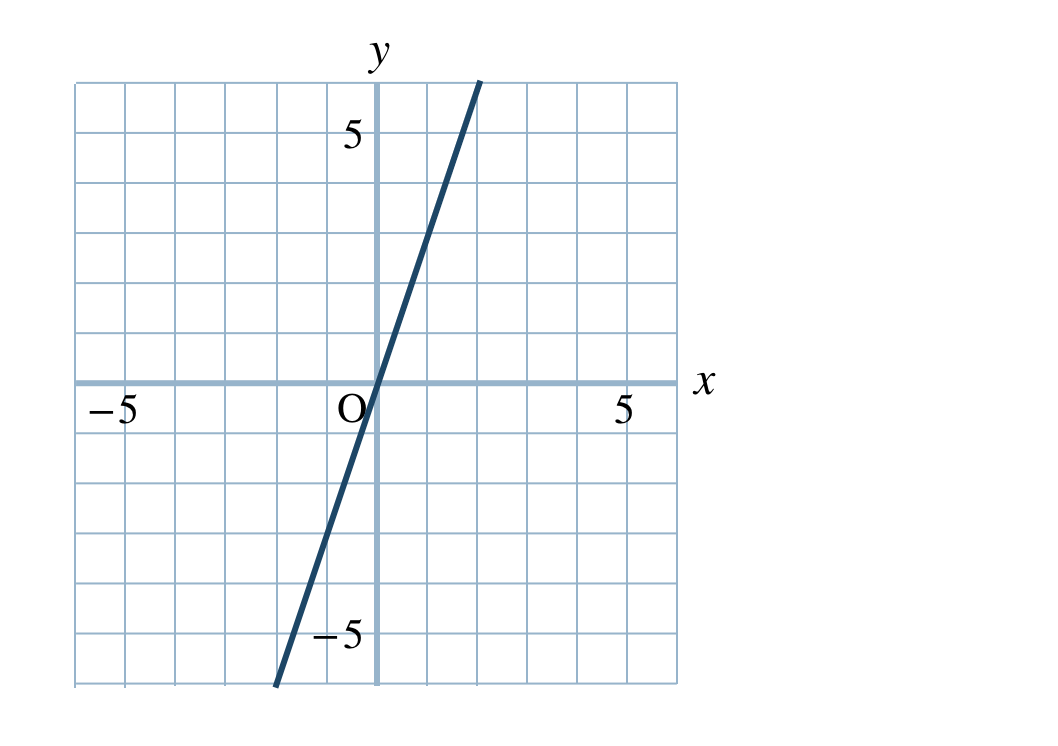

\({\small (2)}~\)

\({\small (3)}~\)

\({\small (4)}~\)

p.126 問4\(x\) の値が増加すると \(y\) の値が増加 → (1) と (3)
\(x\) の値が増加すると \(y\) の値が減少 → (2) と (4)

p.127 練習問題 1

p.127 練習問題 2\({\small (1)}~\)③　　\({\small (2)}~\)④　　\({\small (3)}~\)①　　\({\small (4)}~\)⑤

p.129 問1

---

\(\begin{split}{\small (1)}~y=\frac{\,50\,}{\,x\,}\end{split}\) となり、\(y\) は \(x\) に反比例する

---

　比例定数は \(50\)

---

\(\begin{split}{\small (2)}~y=\frac{\,36\,}{\,x\,}\end{split}\) となり、\(y\) は \(x\) に反比例する

---

　比例定数は \(36\)

p.130 問2\(y\) の値は、
　\(1~,~1.2~,~1.5~,~2~,~3~,~6~,~{\, \small \times \,}~,~\)
　\(-6~,~-3~,~-2~,~-1.5~,~-1.2~,~-1\)

---

(ア) \(x\) の値が \(2\) 倍、\(3\) 倍、\(4\) 倍、…となると、

---

\(y\) の値が \(\begin{split}\frac{\,1\,}{\,2\,}\end{split}\) 倍、\(\begin{split}\frac{\,1\,}{\,3\,}\end{split}\) 倍、\(\begin{split}\frac{\,1\,}{\,4\,}\end{split}\) 倍、…となっている

---

(イ) 対応する \(x\) と \(y\) の値の積は \(-6\) で、比例定数 \(-6\) と等しい

p.131 説明しよう(ア) が反比例の関係
\(x\) と \(y\) の積 \(xy\) が、
\(\begin{split}~~~1\times (-12)=-12~,~2\times(-6)=-12~,~\end{split}\)
\(\begin{split}~~~3\times(-4)=-12~,~4\times(-3)=-12\end{split}\)
よって、一定となるので、\(y\) は \(x\) に反比例している

p.131 問3

---

\(\begin{split}{\small (1)}~y=\frac{\,20\,}{\,x\,}\end{split}\)　　\(\begin{split}{\small (2)}~y=-\frac{\,36\,}{\,x\,}\end{split}\)

p.131 練習問題 1

---

(ア)\(\begin{split}~~y=\frac{\,6\,}{\,x\,}\end{split}\)　　(ウ)\(\begin{split}~~y=\frac{\,800\,}{\,x\,}\end{split}\)

p.132 問1\(x=10~,~100~,~1000~,~10000~,~\cdots\) のとき、
\(y\) の値は、
\(\begin{split}~~~0.6~,~0.06~,~0.006~,~0.0006~,~\cdots\end{split}\)

---

\(x=0.1~,~0.01~,~0.001~,~0.0001~,~\cdots\) のとき、
\(y\) の値は、
\(\begin{split}~~~60~,~600~,~6000~,~60000~,~\cdots\end{split}\)

p.133 問2

p.132 問3

p.136 練習問題 1\({\small (1)}~\)
\({\small (2)}~\)

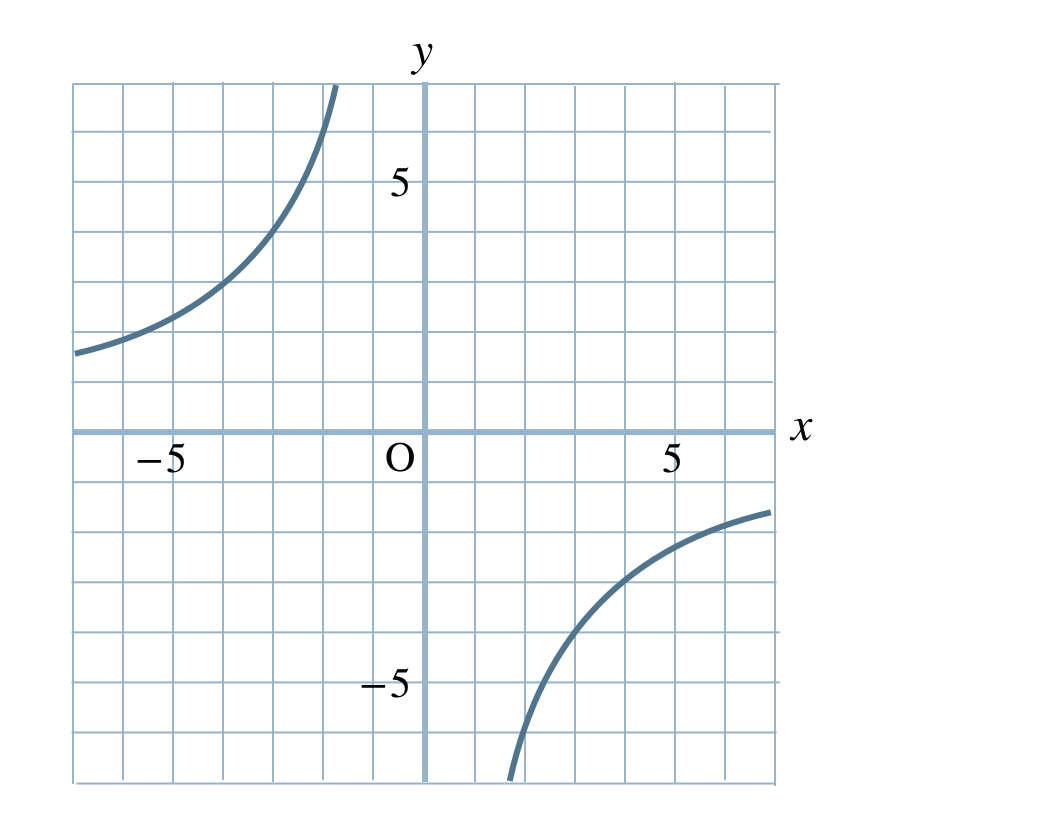
p.136 練習問題 2\({\small (1)}~\)②　　\({\small (2)}~\)③　　\({\small (3)}~\)①

p.138 問1\(\begin{split}~~~y=5x\end{split}\)

p.138 問2　\(5200~{\rm kg}\) で、\(26000\) 個
　\(4800~{\rm kg}\) で、\(24000\) 個

p.139 問3　けいたさん　分速 \(200~{\rm m}\)
　かりんさん　分速 \(150~{\rm m}\)

p.139 問4\({\small (1)}~\)けいたさん\(\begin{split}~y=200x~,~0≦x≦15\end{split}\)
　かりんさん\(\begin{split}~y=150~,~0≦x≦15\end{split}\)

---

\({\small (2)}~\)けいたさん\(\begin{split}~0≦y≦3000\end{split}\)
　かりんさん\(\begin{split}~0≦y≦2250\end{split}\)

p.139 問5\(~~~400~{\rm m}\)

p.140 問6\(~~~4\) 分 \(10\) 秒

p.140 問7\(~~~1\) 分 \(30\) 秒