【ご注意ください】このページの内容について
このページは、旧版教科書に基づいて作成された内容です。
現在の教科書とは一部内容や表現が異なる場合があります。
順次、最新版に対応したページへと更新を進めておりますので、ご了承ください。
このページは、日本文教出版:中学数学1
4章 比例と反比例
4章 比例と反比例

教科書に完全対応の問題集|教科書ぴったりトレーニング
教科書に対応した数学の問題集|教科書ぴったりトレーニングの紹介 こんにちは、みなさん!今回は中学生の...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
日本文教出版中1 1章 正の数と負の数(令和7年度対応)
日本文教出版中1 2章 文字と式(令和7年度対応)
日本文教出版中1 3章 方程式(令和7年度対応)
日本文教出版中1 4章 比例と反比例
日本文教出版中1 5章 平面図形
日本文教出版中1 6章 空間図形
日本文教出版中1 7章 データの活用
4章 比例と反比例
1節 関数
p.127 問2 いえる
■ 同じタイプの例題解説
» 変数と関数
» 変数と関数
p.127 問3\(\begin{split}{\small (1)}~\end{split}\)いえる \(\begin{split}{\small (2)}~\end{split}\)いえる
\(\begin{split}{\small (3)}~\end{split}\)いえる \(\begin{split}{\small (4)}~\end{split}\)いえない
\(\begin{split}{\small (3)}~\end{split}\)いえる \(\begin{split}{\small (4)}~\end{split}\)いえない
■ 同じタイプの例題解説
» 変数と関数
» 変数と関数
p.127 問4\(\begin{split}{\small (1)}~\end{split}\)いえる \(\begin{split}{\small (2)}~\end{split}\)いえない
■ 同じタイプの例題解説
» 変数と関数
» 変数と関数
2節 比例
p.129 問1
\(\begin{split}\frac{\,4\,}{\,1\,}=4~,~\frac{\,8\,}{\,2\,}=4~,~\frac{\,12\,}{\,3\,}=4~,~\end{split}\)
\(\begin{split}\frac{\,16\,}{\,4\,}=4~,~\frac{\,20\,}{\,5\,}=4~,~\frac{\,24\,}{\,6\,}=4~,~\end{split}\)
\(\begin{split}\frac{\,y\,}{\,x\,}\end{split}\) がすべて \(4\) となり、比例定数と等しくなる
\(\begin{split}\frac{\,4\,}{\,1\,}=4~,~\frac{\,8\,}{\,2\,}=4~,~\frac{\,12\,}{\,3\,}=4~,~\end{split}\)
\(\begin{split}\frac{\,16\,}{\,4\,}=4~,~\frac{\,20\,}{\,5\,}=4~,~\frac{\,24\,}{\,6\,}=4~,~\end{split}\)
\(\begin{split}\frac{\,y\,}{\,x\,}\end{split}\) がすべて \(4\) となり、比例定数と等しくなる
■ 同じタイプの例題解説
» 比例の関係
» 比例の関係
p.11 問11\(\begin{split}{\small (1)}~y=45x\end{split}\)
\(y\) は \(x\) に比例し、比例定数 \(45\)
\(\begin{split}{\small (2)}~y=5x\end{split}\)
\(y\) は \(x\) に比例し、比例定数 \(5\)
\(y\) は \(x\) に比例し、比例定数 \(45\)
\(\begin{split}{\small (2)}~y=5x\end{split}\)
\(y\) は \(x\) に比例し、比例定数 \(5\)
■ 同じタイプの例題解説
» 比例の式
» 比例の式
p.131 問1\(\begin{split}{\small (1)}~x>2\end{split}\) \(\begin{split}{\small (2)}~x≧5\end{split}\)
\(\begin{split}{\small (3)}~x<10\end{split}\) \(\begin{split}{\small (4)}~x≦12\end{split}\)
\(\begin{split}{\small (5)}~1≦x≦9\end{split}\) \(\begin{split}{\small (6)}~0≦x<7\end{split}\)
\(\begin{split}{\small (7)}~4<x<24\end{split}\)
\(\begin{split}{\small (3)}~x<10\end{split}\) \(\begin{split}{\small (4)}~x≦12\end{split}\)
\(\begin{split}{\small (5)}~1≦x≦9\end{split}\) \(\begin{split}{\small (6)}~0≦x<7\end{split}\)
\(\begin{split}{\small (7)}~4<x<24\end{split}\)
■ 同じタイプの例題解説
» 変域の表し方
» 変域の表し方
p.131 問2 \(0≦y≦24\)
■ 同じタイプの例題解説
» 変域の表し方
» 変域の表し方
p.131 問3\(\begin{split}{\small (1)}~y=90x\end{split}\)
\(\begin{split}{\small (2)}~0≦x≦85~,~0≦y≦7650\end{split}\)
\(\begin{split}{\small (2)}~0≦x≦85~,~0≦y≦7650\end{split}\)
■ 同じタイプの例題解説
» 変域の表し方
» 変域の表し方
p.132 問1\(\begin{split}{\small (1)}~\end{split}\)\(2\) 倍、\(3\) 倍…となる
\(\begin{split}{\small (2)}~\end{split}\)すべて \(60\) となり、比例定数と等しい
\(\begin{split}{\small (2)}~\end{split}\)すべて \(60\) となり、比例定数と等しい
■ 同じタイプの例題解説
» 比例の関係
» 比例の関係
p.133 問2\(\begin{split}{\small (1)}~\end{split}\)\(2\) 倍、\(3\) 倍…となる
\(\begin{split}{\small (2)}~\end{split}\)すべて \(-4\) となり、比例定数と等しい
\(\begin{split}{\small (2)}~\end{split}\)すべて \(-4\) となり、比例定数と等しい
■ 同じタイプの例題解説
» 比例の関係
» 比例の関係
p.133 問3\(x\) の値が \(m\) 倍になると、それに対応する \(y\) の値も \(m\) になる
\(x\neq 0\) のとき、対応する \(x\) と \(y\) の値の商 \(\begin{split}\frac{\,y\,}{\,x\,}\end{split}\) は一定で、比例定数に等しい
\(x\neq 0\) のとき、対応する \(x\) と \(y\) の値の商 \(\begin{split}\frac{\,y\,}{\,x\,}\end{split}\) は一定で、比例定数に等しい
■ 同じタイプの例題解説
» 比例の関係
» 比例の関係
p.133 問4問1では、\(x=2\) のとき \(y=120\)
\(x\) を \(\begin{split}\frac{\,1\,}{\,2\,}\end{split}\) 倍した \(x=1\) のとき
\(y=60\) となり、\(y\) も \(\begin{split}\frac{\,1\,}{\,2\,}\end{split}\) 倍されている
問2では、\(x=2\) のとき \(y=-8\)
\(x\) を \(\begin{split}\frac{\,1\,}{\,2\,}\end{split}\) 倍した \(x=1\) のとき
\(y=-4\) となり、\(y\) も \(\begin{split}\frac{\,1\,}{\,2\,}\end{split}\) 倍されている
\(x\) を \(\begin{split}\frac{\,1\,}{\,2\,}\end{split}\) 倍した \(x=1\) のとき
\(y=60\) となり、\(y\) も \(\begin{split}\frac{\,1\,}{\,2\,}\end{split}\) 倍されている
問2では、\(x=2\) のとき \(y=-8\)
\(x\) を \(\begin{split}\frac{\,1\,}{\,2\,}\end{split}\) 倍した \(x=1\) のとき
\(y=-4\) となり、\(y\) も \(\begin{split}\frac{\,1\,}{\,2\,}\end{split}\) 倍されている
■ 同じタイプの例題解説
» 比例の関係
» 比例の関係
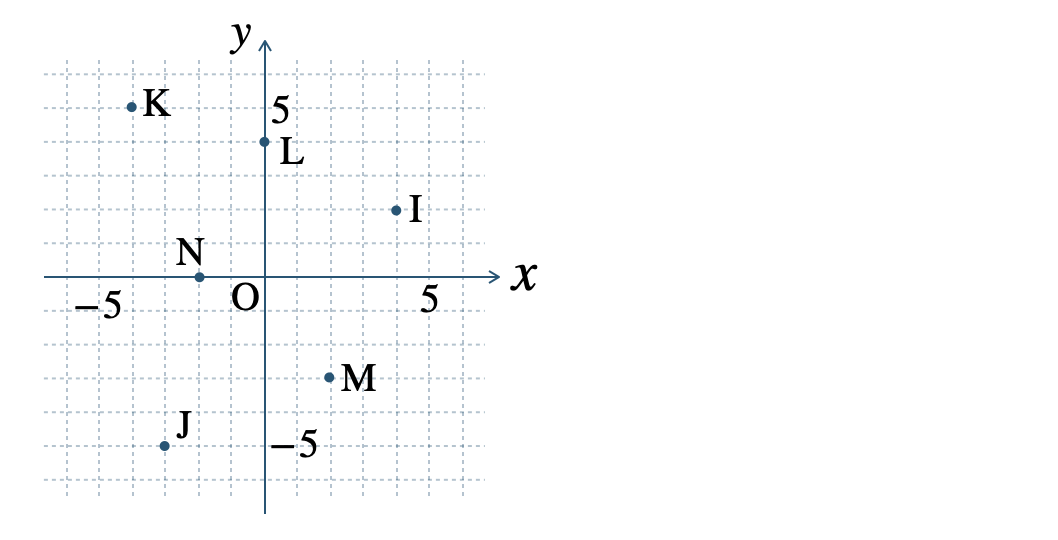
p.135 問1 \(\begin{split}{\rm A}(2~,~4)~,~{\rm B}(0~,~2)~,~{\rm C}(-5~,~0)\end{split}\)
\(\begin{split}{\rm D}(-5~,~-5)~,~{\rm E}(0~,~-3)~,~{\rm F}(3~,~-4)\end{split}\)
\(\begin{split}{\rm G}(4~,~0)~,~{\rm H}(-3~,~1)\end{split}\)
\(\begin{split}{\rm D}(-5~,~-5)~,~{\rm E}(0~,~-3)~,~{\rm F}(3~,~-4)\end{split}\)
\(\begin{split}{\rm G}(4~,~0)~,~{\rm H}(-3~,~1)\end{split}\)
■ 同じタイプの例題解説
» 座標と点の表し方
» 座標と点の表し方
p.136 問1\(\begin{split}{\small (1)}~\end{split}\)\(y\) の値は、
\(-8~,~-6~,~-4~,~-2~,~0~,~2~,~4~,~6~,~8\)
\(\begin{split}{\small (2)}~\end{split}\)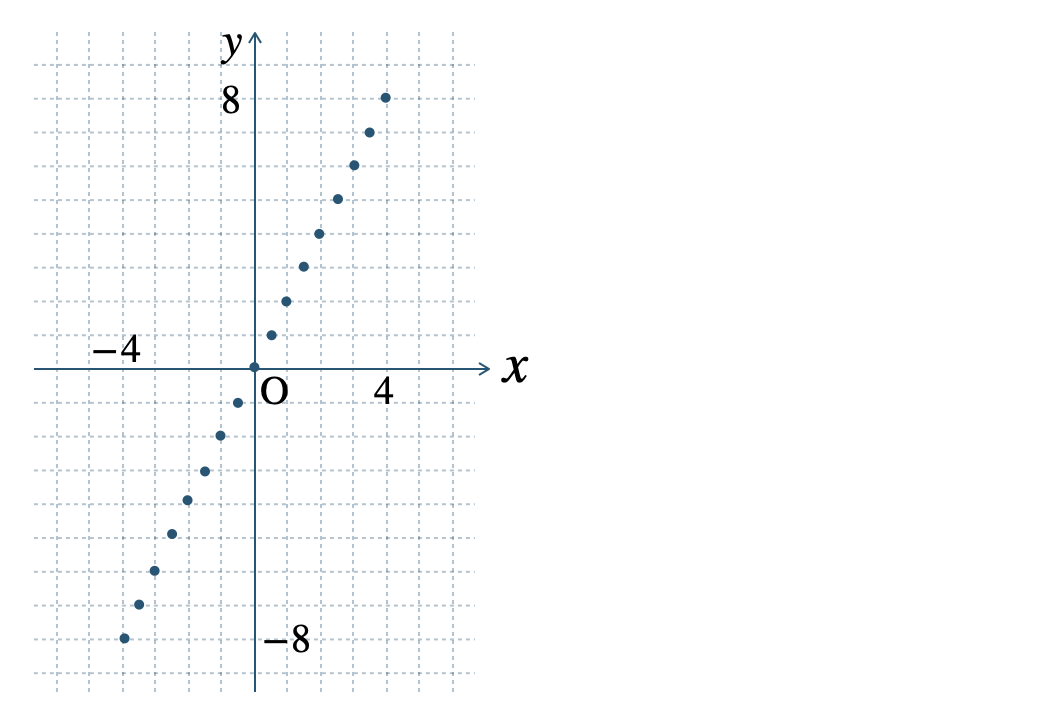
\(-8~,~-6~,~-4~,~-2~,~0~,~2~,~4~,~6~,~8\)
\(\begin{split}{\small (2)}~\end{split}\)

\(\begin{split}{\small (3)}~\end{split}\)直線になる
■ 同じタイプの例題解説
» 比例のグラフ
» 比例のグラフ
p.137 問2\(\begin{split}{\small (1)}~\end{split}\)
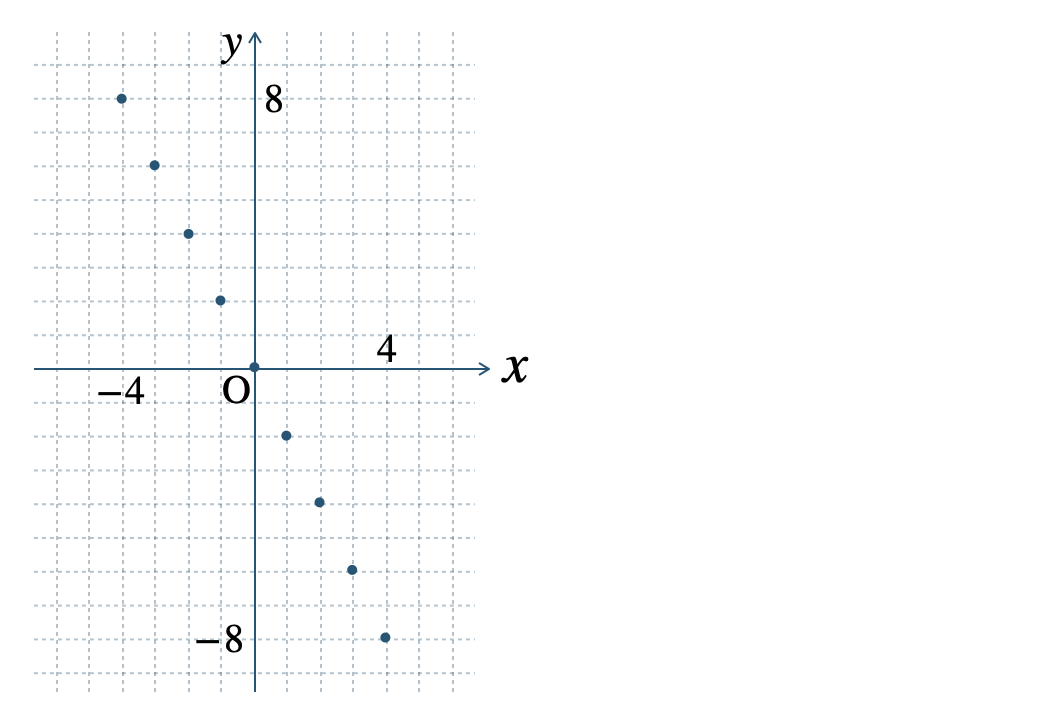
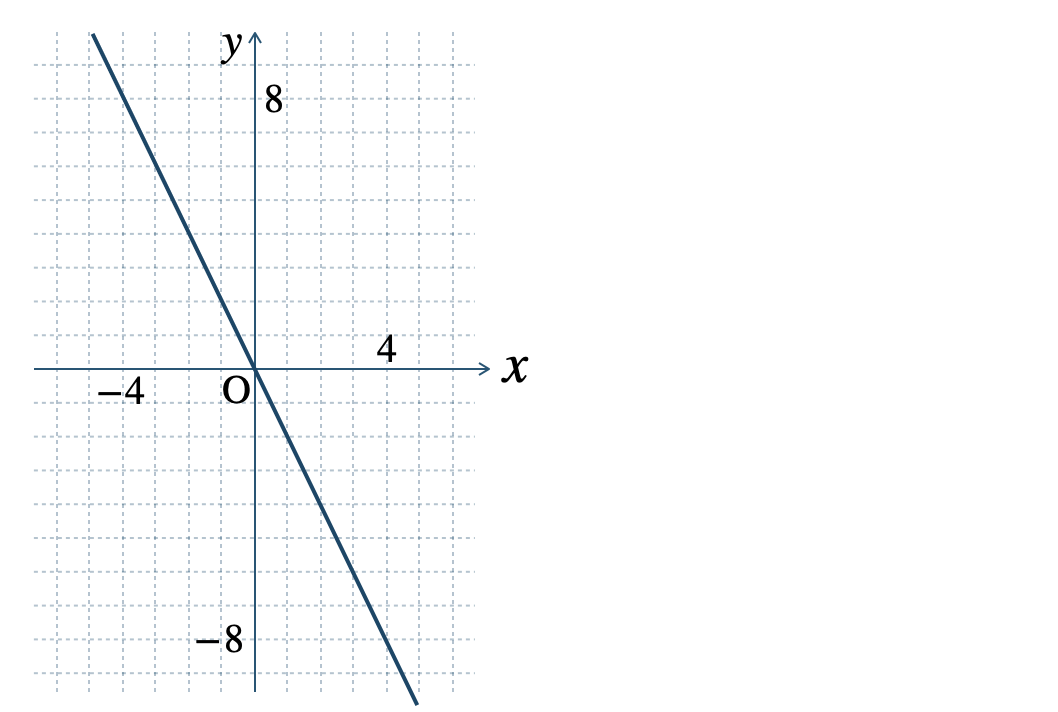

\(\begin{split}{\small (2)}~\end{split}\)

■ 同じタイプの例題解説
» 比例のグラフ
» 比例のグラフ
p.138 問1\(\begin{split}{\small (1)}~\end{split}\)

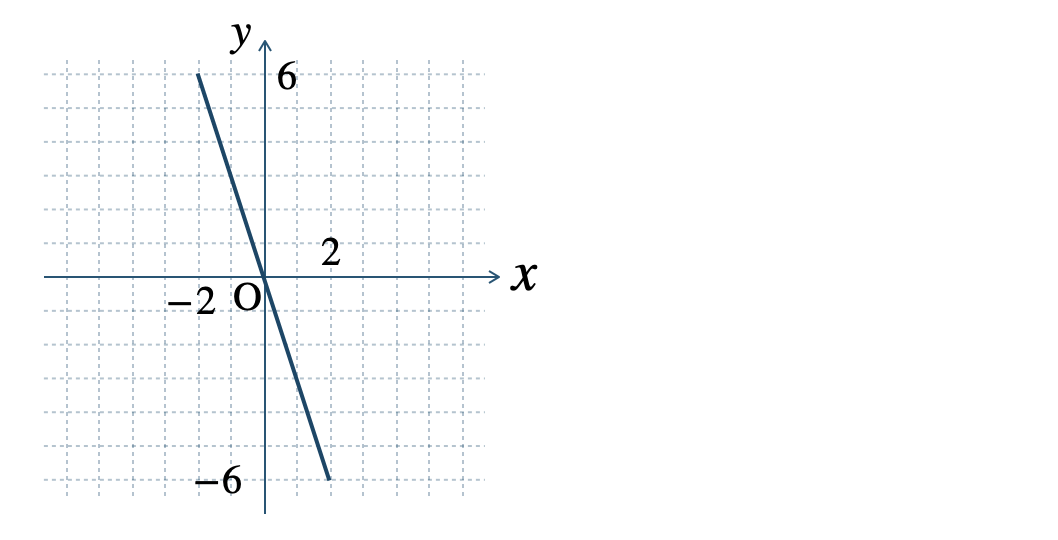

\(\begin{split}{\small (2)}~\end{split}\)

■ 同じタイプの例題解説
» 比例のグラフ
» 比例のグラフ
p.139 問3\(\begin{split}{\small (1)}~\end{split}\)
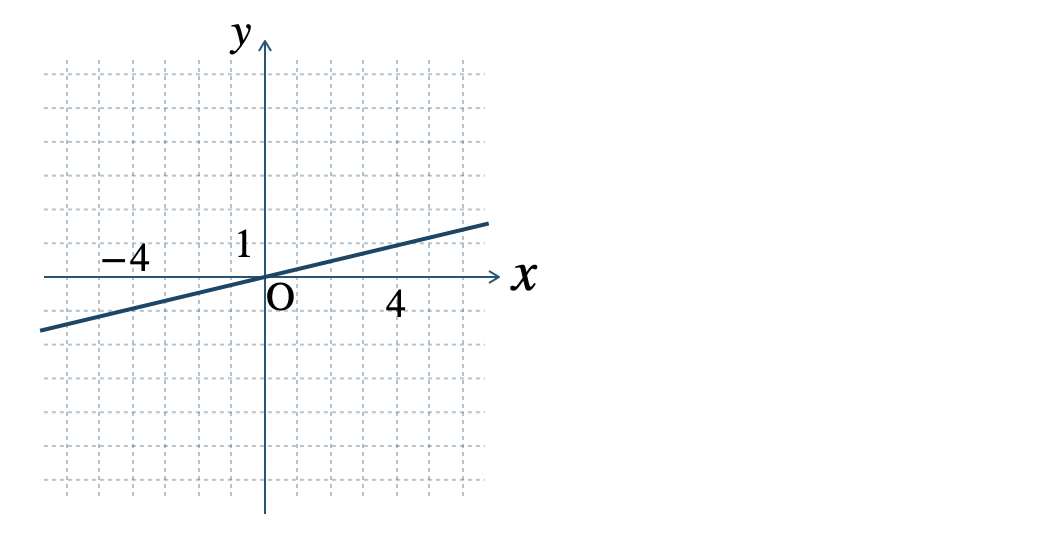
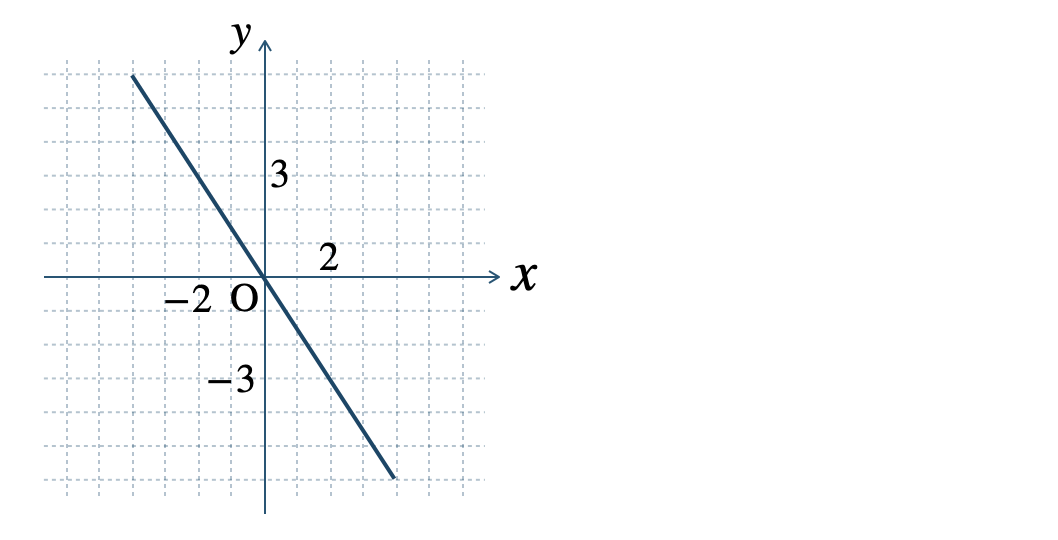

\(\begin{split}{\small (2)}~\end{split}\)
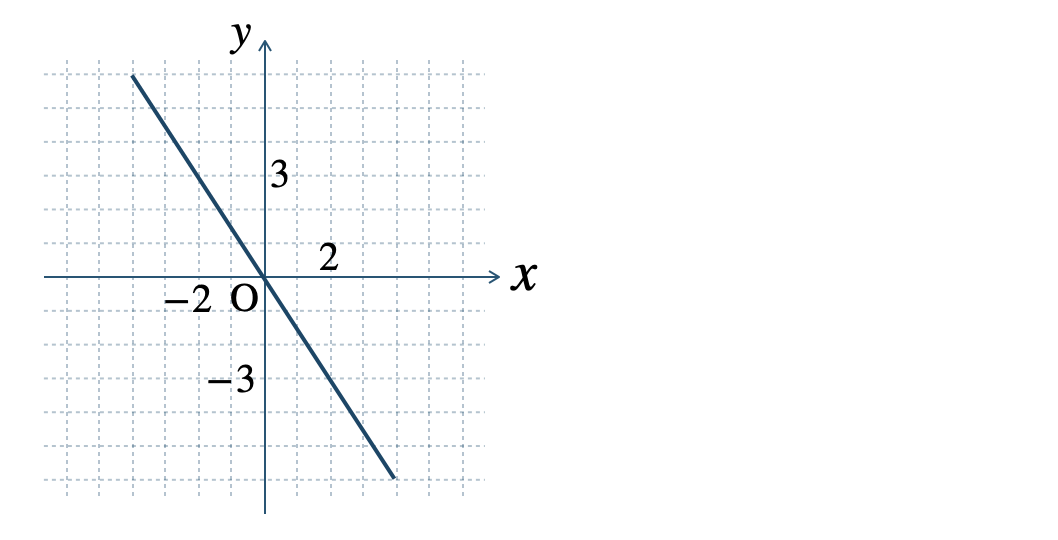
■ 同じタイプの例題解説
» 比例のグラフ
» 比例のグラフ
p.139 問4\(\begin{split}{\small (1)}~\end{split}\)\(y\) の値は \(2\) 増加する
\(\begin{split}{\small (2)}~\end{split}\)上の方向へ \(2\) めもり進む
\(\begin{split}{\small (2)}~\end{split}\)上の方向へ \(2\) めもり進む
■ 同じタイプの例題解説
» 比例のグラフ
» 比例のグラフ
p.140 問5\(\begin{split}{\small (1)}~\end{split}\)\(y\) の値は \(2\) 減少する
\(\begin{split}{\small (2)}~\end{split}\)下の方向へ \(2\) めもり進む
\(\begin{split}{\small (2)}~\end{split}\)下の方向へ \(2\) めもり進む
■ 同じタイプの例題解説
» 比例のグラフ
» 比例のグラフ
p.140 問6表では、\(x\) が \(1\) ずつ増えると \(y\) が \(2\) ずつ減少する
グラフでは、右に \(1\) めもり進むと、下に \(2\) めもり進む
グラフでは、右に \(1\) めもり進むと、下に \(2\) めもり進む
■ 同じタイプの例題解説
» 比例のグラフ
» 比例のグラフ
p.141 問1\(\begin{split}{\small (1)}~y=4x\end{split}\)、\(x=-2\) のとき、\(y=-8\)
\(\begin{split}{\small (2)}~y=-9x\end{split}\)、\(y=5\) のとき、\(\begin{split}x=-\frac{\,5\,}{\,9\,}\end{split}\)
\(\begin{split}{\small (2)}~y=-9x\end{split}\)、\(y=5\) のとき、\(\begin{split}x=-\frac{\,5\,}{\,9\,}\end{split}\)
■ 同じタイプの例題解説
» 比例の式
» 比例の式
p.142 問2\(\begin{split}{\small (1)}~y=18x\end{split}\) \(\begin{split}{\small (2)}~144~{\rm km}\end{split}\)
\(\begin{split}{\small (3)}~30~{\rm L}\end{split}\)
\(\begin{split}{\small (3)}~30~{\rm L}\end{split}\)
■ 同じタイプの例題解説
» 比例の利用
» 比例の利用
p.142 問3
\(\begin{split}{\small (1)}~y=4x\end{split}\) \(\begin{split}{\small (2)}~y=-\frac{\,2\,}{\,5\,}x\end{split}\)
\(\begin{split}{\small (1)}~y=4x\end{split}\) \(\begin{split}{\small (2)}~y=-\frac{\,2\,}{\,5\,}x\end{split}\)
■ 同じタイプの例題解説
» グラフと比例・反比例の式
» グラフと比例・反比例の式
p.142 問4 \(y=-5x\)
■ 同じタイプの例題解説
» グラフと比例・反比例の式
» グラフと比例・反比例の式
基本の問題
p.143 基本の問題 1\(\begin{split}{\small (1)}~6~,~-9\end{split}\) \(\begin{split}{\small (2)}~2\end{split}\) 倍、\(-3\)
\(\begin{split}{\small (3)}~y=-3x\end{split}\) \(\begin{split}{\small (4)}~-3\end{split}\)
\(\begin{split}{\small (3)}~y=-3x\end{split}\) \(\begin{split}{\small (4)}~-3\end{split}\)
■ 同じタイプの例題解説
» 比例の関係
» 比例の関係
p.143 基本の問題 2\(\begin{split}{\small (1)}~\end{split}\)
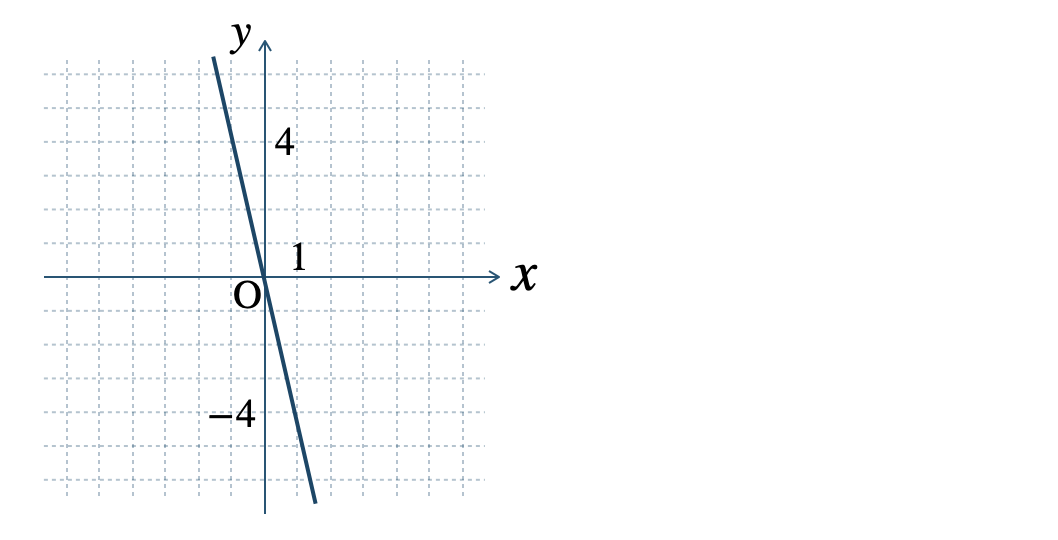
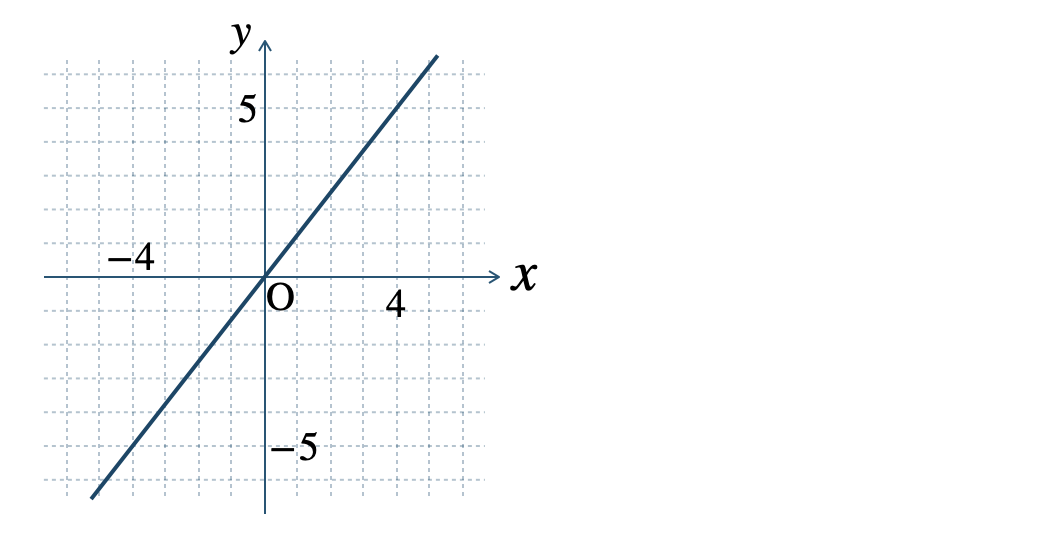

\(\begin{split}{\small (2)}~\end{split}\)

■ 同じタイプの例題解説
» 比例のグラフ
» 比例のグラフ
p.143 基本の問題 3 \(y=-7x\)
■ 同じタイプの例題解説
» 比例の式
» 比例の式
p.143 基本の問題 4\(\begin{split}{\small (1)}~y=5x\end{split}\) \(\begin{split}{\small (2)}~10\end{split}\) 分後
\(\begin{split}{\small (3)}~0≦x≦16\end{split}\)
\(\begin{split}{\small (3)}~0≦x≦16\end{split}\)
■ 同じタイプの例題解説
» 比例の利用
» 比例の利用
3節 反比例
p.145 問1\(1{\, \small \times \,}12=12~,~2{\, \small \times \,}6=12~,~3{\, \small \times \,}4=12\)
\(\begin{split}4{\, \small \times \,}3=12~,~5{\, \small \times \,}\frac{\,12\,}{\,5\,}=12~,~6{\, \small \times \,}2=12\end{split}\)
\(xy\) は一定で、比例定数に等しい
\(\begin{split}4{\, \small \times \,}3=12~,~5{\, \small \times \,}\frac{\,12\,}{\,5\,}=12~,~6{\, \small \times \,}2=12\end{split}\)
\(xy\) は一定で、比例定数に等しい
■ 同じタイプの例題解説
» 反比例の関係
» 反比例の関係
p.145 問2
\(\begin{split}{\small (1)}~y=\frac{\,20\,}{\,x\,}\end{split}\)
反比例して、比例定数は \(20\)
\(\begin{split}{\small (2)}~y=\frac{\,800\,}{\,x\,}\end{split}\)
反比例して、比例定数は \(800\)
\(\begin{split}{\small (1)}~y=\frac{\,20\,}{\,x\,}\end{split}\)
反比例して、比例定数は \(20\)
\(\begin{split}{\small (2)}~y=\frac{\,800\,}{\,x\,}\end{split}\)
反比例して、比例定数は \(800\)
■ 同じタイプの例題解説
» 反比例の式
» 反比例の式
p.145 問3
\(y=-x+10\) となり、\(\begin{split}y=\frac{\,a\,}{\,x\,}\end{split}\) とならないので、反比例するといえない
\(y=-x+10\) となり、\(\begin{split}y=\frac{\,a\,}{\,x\,}\end{split}\) とならないので、反比例するといえない
■ 同じタイプの例題解説
» 反比例の式
» 反比例の式
p.146 問1\(\begin{split}{\small (1)}~24\end{split}\)
\(\begin{split}{\small (2)}~\frac{\,1\,}{\,2\,}\end{split}\) 倍、\(\begin{split}\frac{\,1\,}{\,3\,}\end{split}\) 倍、…となる
\(\begin{split}{\small (3)}~24\end{split}\) となり、比例定数と等しい
\(\begin{split}{\small (2)}~\frac{\,1\,}{\,2\,}\end{split}\) 倍、\(\begin{split}\frac{\,1\,}{\,3\,}\end{split}\) 倍、…となる
\(\begin{split}{\small (3)}~24\end{split}\) となり、比例定数と等しい
■ 同じタイプの例題解説
» 反比例の関係
» 反比例の関係
p.146 問2 ア:比例定数 \(15\) イ:比例定数 \(-15\)
■ 同じタイプの例題解説
» 反比例の式
» 反比例の式
p.147 問3
\(\begin{split}{\small (1)}~\frac{\,1\,}{\,2\,}\end{split}\) 倍、\(\begin{split}\frac{\,1\,}{\,3\,}\end{split}\) 倍、…となる
\(\begin{split}{\small (2)}~-24\end{split}\) となり、比例定数と等しい
\(\begin{split}{\small (1)}~\frac{\,1\,}{\,2\,}\end{split}\) 倍、\(\begin{split}\frac{\,1\,}{\,3\,}\end{split}\) 倍、…となる
\(\begin{split}{\small (2)}~-24\end{split}\) となり、比例定数と等しい
■ 同じタイプの例題解説
» 反比例の関係
» 反比例の関係
p.147 問4\(x\) の値が \(m\) 倍になると、それに対応する \(y\) の値は \(\begin{split}\frac{\,1\,}{\,m\,}\end{split}\) になる
対応する \(x\) と \(y\) の値の積 \(xy\) は一定で、比例定数に等しい
対応する \(x\) と \(y\) の値の積 \(xy\) は一定で、比例定数に等しい
■ 同じタイプの例題解説
» 反比例の関係
» 反比例の関係
p.147 まちがえやすい問題\(1{\, \small \times \,}120=120~,~2{\, \small \times \,}60=120\)
\(3{\, \small \times \,}30=90~,~4{\, \small \times \,}15=60\)
対応する \(x\) と \(y\) の値の積 \(xy\) は一定でないので、反比例するといえない
\(3{\, \small \times \,}30=90~,~4{\, \small \times \,}15=60\)
対応する \(x\) と \(y\) の値の積 \(xy\) は一定でないので、反比例するといえない
■ 同じタイプの例題解説
» 反比例の関係
» 反比例の関係
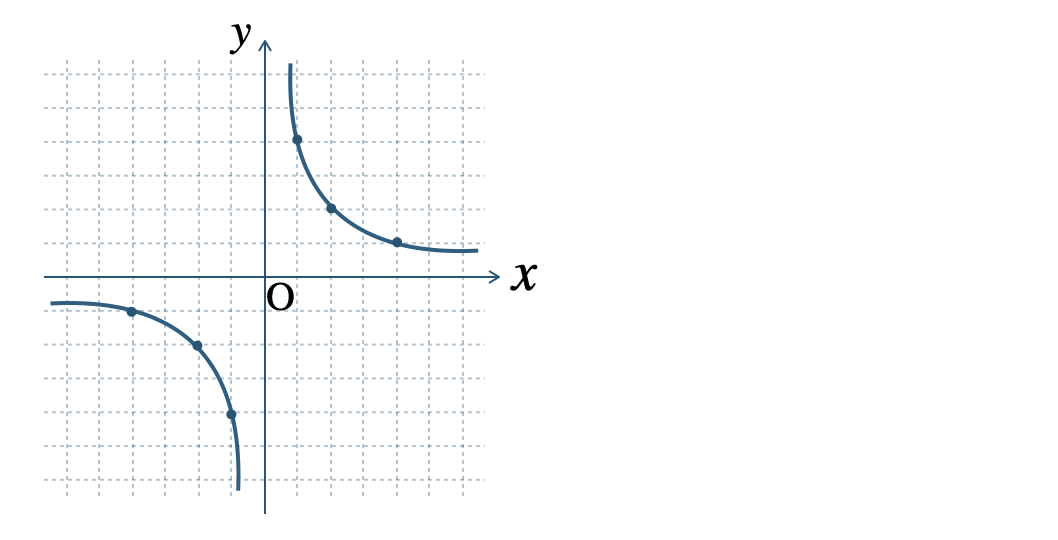
p.148 問1\(\begin{split}{\small (1)}~\end{split}\)\(y\) の値は、
\(\begin{split}-1~,~-\frac{\,6\,}{\,5\,}~,~-\frac{\,3\,}{\,2\,}~,~-2~,~-3~,~-6~,~\end{split}\)
\(\begin{split}{\, \small \times \,}~,~6~,~3~,~2~,~\frac{\,3\,}{\,2\,}~,~\frac{\,6\,}{\,5\,}~,~1\end{split}\)
\(\begin{split}{\small (2)}~\end{split}\)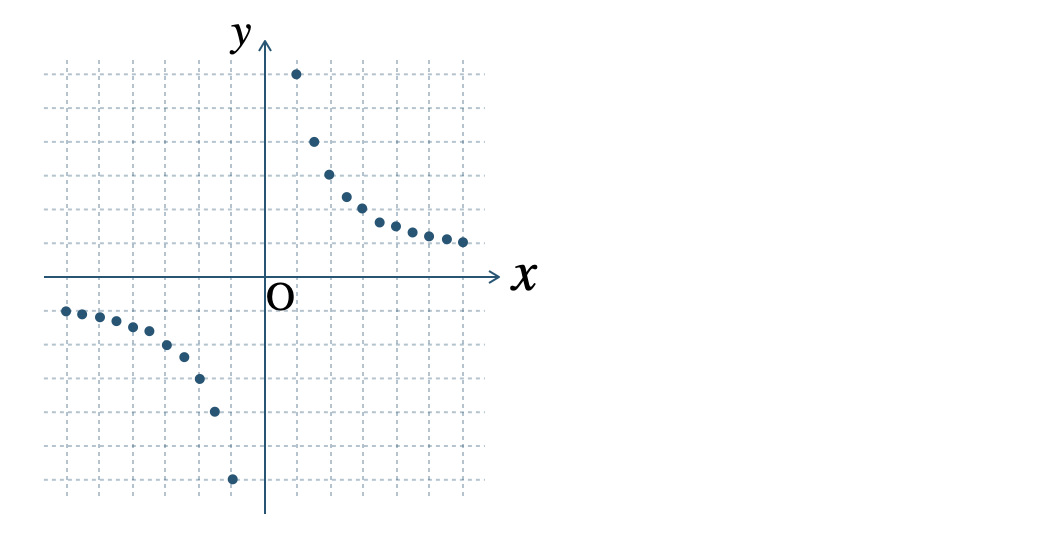
\(\begin{split}-1~,~-\frac{\,6\,}{\,5\,}~,~-\frac{\,3\,}{\,2\,}~,~-2~,~-3~,~-6~,~\end{split}\)
\(\begin{split}{\, \small \times \,}~,~6~,~3~,~2~,~\frac{\,3\,}{\,2\,}~,~\frac{\,6\,}{\,5\,}~,~1\end{split}\)
\(\begin{split}{\small (2)}~\end{split}\)

■ 同じタイプの例題解説
» 反比例のグラフ
» 反比例のグラフ
p.149 問2\(\begin{split}{\small (1)}~\end{split}\)\(y\) の値は \(0.6~,~0.06~,~0.006~,~\cdots\) と小さくなり、グラフは \(x\) 軸に近づく
\(\begin{split}{\small (2)}~\end{split}\)\(y\) の値は \(0~,~60~,~600~,~6000~,~\cdots\) と大きくなり、グラフは \(y\) 軸に近づく
\(\begin{split}{\small (2)}~\end{split}\)\(y\) の値は \(0~,~60~,~600~,~6000~,~\cdots\) と大きくなり、グラフは \(y\) 軸に近づく
■ 同じタイプの例題解説
» 反比例のグラフ
» 反比例のグラフ
p.150 問5\(\begin{split}{\small (1)}~\end{split}\)ア:\(y\) の値は減少する
イ:\(y\) の値は増加する
\(\begin{split}{\small (2)}~\end{split}\)ア:\(y\) の値は減少する
イ:\(y\) の値は増加する
イ:\(y\) の値は増加する
\(\begin{split}{\small (2)}~\end{split}\)ア:\(y\) の値は減少する
イ:\(y\) の値は増加する
■ 同じタイプの例題解説
» 反比例のグラフ
» 反比例のグラフ
p.150 問6\(\begin{split}{\small (1)}~\end{split}\)グラフの形(双曲線)
\(x\) 軸、\(y\) 軸に重ならない
\(\begin{split}{\small (2)}~\end{split}\)\(x\) の値を大きくするときの \(y\) こ値の変わり方
グラフの位置
\(x\) 軸、\(y\) 軸に重ならない
\(\begin{split}{\small (2)}~\end{split}\)\(x\) の値を大きくするときの \(y\) こ値の変わり方
グラフの位置
■ 同じタイプの例題解説
» 反比例のグラフ
» 反比例のグラフ
p.151 問1
\(\begin{split}{\small (1)}~y=\frac{\,28\,}{\,x\,}\end{split}\)、\(x=7\) のとき \(y=4\)
\(\begin{split}{\small (2)}~y=-\frac{\,100\,}{\,x\,}\end{split}\)、\(y=-4\) のとき \(x=25\)
\(\begin{split}{\small (1)}~y=\frac{\,28\,}{\,x\,}\end{split}\)、\(x=7\) のとき \(y=4\)
\(\begin{split}{\small (2)}~y=-\frac{\,100\,}{\,x\,}\end{split}\)、\(y=-4\) のとき \(x=25\)
■ 同じタイプの例題解説
» 反比例の式
» 反比例の式
p.151 問2
\(\begin{split}{\small (1)}~y=\frac{\,120\,}{\,x\,}\end{split}\) \(\begin{split}{\small (2)}~3\end{split}\) 時間
\(\begin{split}{\small (3)}~2≦y≦3\end{split}\)
\(\begin{split}{\small (1)}~y=\frac{\,120\,}{\,x\,}\end{split}\) \(\begin{split}{\small (2)}~3\end{split}\) 時間
\(\begin{split}{\small (3)}~2≦y≦3\end{split}\)
■ 同じタイプの例題解説
» 反比例の利用
» 反比例の利用
p.152 問4
\(\begin{split}{\small (1)}~y=\frac{\,15\,}{\,x\,}\end{split}\) \(\begin{split}{\small (2)}~y=-\frac{\,14\,}{\,x\,}\end{split}\)
\(\begin{split}{\small (1)}~y=\frac{\,15\,}{\,x\,}\end{split}\) \(\begin{split}{\small (2)}~y=-\frac{\,14\,}{\,x\,}\end{split}\)
■ 同じタイプの例題解説
» グラフと比例・反比例の式
» グラフと比例・反比例の式
基本の問題
p.153 基本の問題 1
\(\begin{split}{\small (1)}~-6~,~4\end{split}\) \(\begin{split}{\small (2)}~12\end{split}\)、\(\begin{split}\frac{\,1\,}{\,3\,}\end{split}\) 倍
\(\begin{split}{\small (3)}~y=\frac{\,12\,}{\,x\,}\end{split}\) \(\begin{split}{\small (4)}~12\end{split}\)
\(\begin{split}{\small (1)}~-6~,~4\end{split}\) \(\begin{split}{\small (2)}~12\end{split}\)、\(\begin{split}\frac{\,1\,}{\,3\,}\end{split}\) 倍
\(\begin{split}{\small (3)}~y=\frac{\,12\,}{\,x\,}\end{split}\) \(\begin{split}{\small (4)}~12\end{split}\)
■ 同じタイプの例題解説
» 反比例の関係
» 反比例の関係
p.153 基本の問題 4\(\begin{split}{\small (1)}~y=\frac{\,48\,}{\,x\,}\end{split}\) \(\begin{split}{\small (2)}~16\end{split}\) 分
\(\begin{split}{\small (3)}~0≦y≦24\end{split}\)
\(\begin{split}{\small (3)}~0≦y≦24\end{split}\)
■ 同じタイプの例題解説
» 反比例の利用
» 反比例の利用
4節 比例と反比例の活用
p.154 問1\(\begin{split}{\small (1)}~1~{\rm L}\end{split}\) の海水からとれる塩の量
\(\begin{split}{\small (2)}~\end{split}\)約 \(32~{\rm L}\)
\(\begin{split}{\small (2)}~\end{split}\)約 \(32~{\rm L}\)
■ 同じタイプの例題解説
» 比例の利用
» 比例の利用
p.155 問2
\(\begin{split}{\small (1)}~y=\frac{\,120\,}{\,x\,}\end{split}\) より、\(x=60\) のとき \(y=2\)
\(\begin{split}{\small (2)}~\end{split}\)\(x=10\) のとき \(y=12\) より、
\(x\) を \(6\) 倍すると、\(y\) は \(\begin{split}\frac{\,1\,}{\,6\,}\end{split}\) 倍となるので \(y=2\)
\(\begin{split}{\small (1)}~y=\frac{\,120\,}{\,x\,}\end{split}\) より、\(x=60\) のとき \(y=2\)
\(\begin{split}{\small (2)}~\end{split}\)\(x=10\) のとき \(y=12\) より、
\(x\) を \(6\) 倍すると、\(y\) は \(\begin{split}\frac{\,1\,}{\,6\,}\end{split}\) 倍となるので \(y=2\)
■ 同じタイプの例題解説
» 反比例の利用
» 反比例の利用
p.156 問1\(\begin{split}{\small (1)}~y=75x~,~0≦x≦8\end{split}\)
\(\begin{split}{\small (2)}~\end{split}\)歩いた速さ
\(\begin{split}{\small (2)}~\end{split}\)歩いた速さ
■ 同じタイプの例題解説
» 比例の利用
» 比例の利用
p.156 問2\(\begin{split}{\small (1)}~\end{split}\)
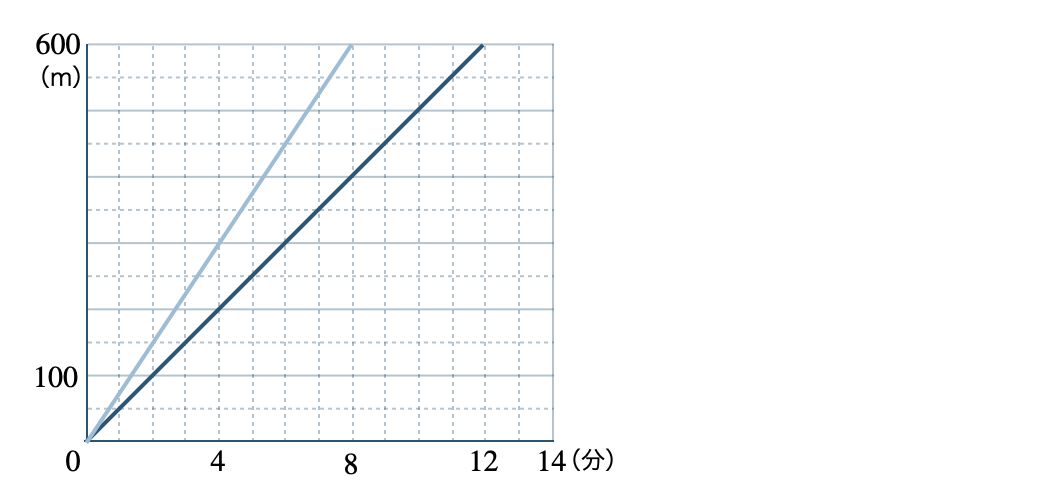

\(\begin{split}{\small (2)}~400~{\rm m}\end{split}\) \(\begin{split}{\small (3)}~100~{\rm m}\end{split}\)
■ 同じタイプの例題解説
» 比例の利用
» 比例の利用
次のページ「5章 平面図形」