【ご注意ください】このページの内容について
このページは、旧版教科書に基づいて作成された内容です。
現在の教科書とは一部内容や表現が異なる場合があります。
順次、最新版に対応したページへと更新を進めておりますので、ご了承ください。
このページは、啓林館:未来へ広がる数学3
4章 関数y=ax²
4章 関数y=ax²

教科書に完全対応の問題集|教科書ぴったりトレーニング
教科書に対応した数学の問題集|教科書ぴったりトレーニングの紹介 こんにちは、みなさん!今回は中学生の...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
啓林館中3 1章 式の展開と因数分解(令和7年度対応)
啓林館中3 2章 平方根(令和7年度対応)
啓林館中3 3章 二次方程式(令和7年度対応)
啓林館中3 4章 関数y=ax²
啓林館中3 5章 図形と相似
啓林館中3 6章 円の性質
啓林館中3 7章 三平方の定理
啓林館中3 8章 標本調査とデータの活用
4章 関数y=ax²
1節 関数とグラフ
1 関数y=ax²
p.93 問1\(\begin{split}~~~y=2x^2\end{split}\)
■ 同じタイプの例題解説
» 2乗に比例する関数
» 2乗に比例する関数
p.93 問2\(\begin{split}~~~y=\pi x^2\end{split}\)
\(4\) 倍、\(9\) 倍、\(16\) 倍、…となる
\(4\) 倍、\(9\) 倍、\(16\) 倍、…となる
■ 同じタイプの例題解説
» 2乗に比例する関数
» 2乗に比例する関数
p.94 問3\(\begin{split}{\small (1)}~y=3x^2\end{split}\) \(\begin{split}{\small (2)}~y=8x^2\end{split}\)
■ 同じタイプの例題解説
» 関数y=ax²の式
» 関数y=ax²の式
p.94 練習問題 1 \(3\) 秒
■ 同じタイプの例題解説
» 2乗に比例する関数
» 2乗に比例する関数
p.94 練習問題 2\(\begin{split}{\small (1)}~y=-2x^2\end{split}\) \(\begin{split}{\small (2)}~y=-50\end{split}\)
■ 同じタイプの例題解説
» 関数y=ax²の式
» 関数y=ax²の式
2 関数y=ax²のグラフ
p.95 問1\(\begin{split}&(-3~,~9)~,~(-2.5~,~6.25)\\[2pt]~~~&(-2~,~4)~,~(-1.5~,~2.25)\\[2pt]~~~&(-1~,~1)~,~(-0.5~,~0.25)\\[2pt]~~~&(0~,~0)~,~(0.5~,~0.25)\\[2pt]~~~&(1~,~1)~,~(1.5~,~2.25)\\[2pt]~~~&(2~,~4)~,~(2.5~,~6.25)\\[2pt]~~~&(3~,~9)\end{split}\)
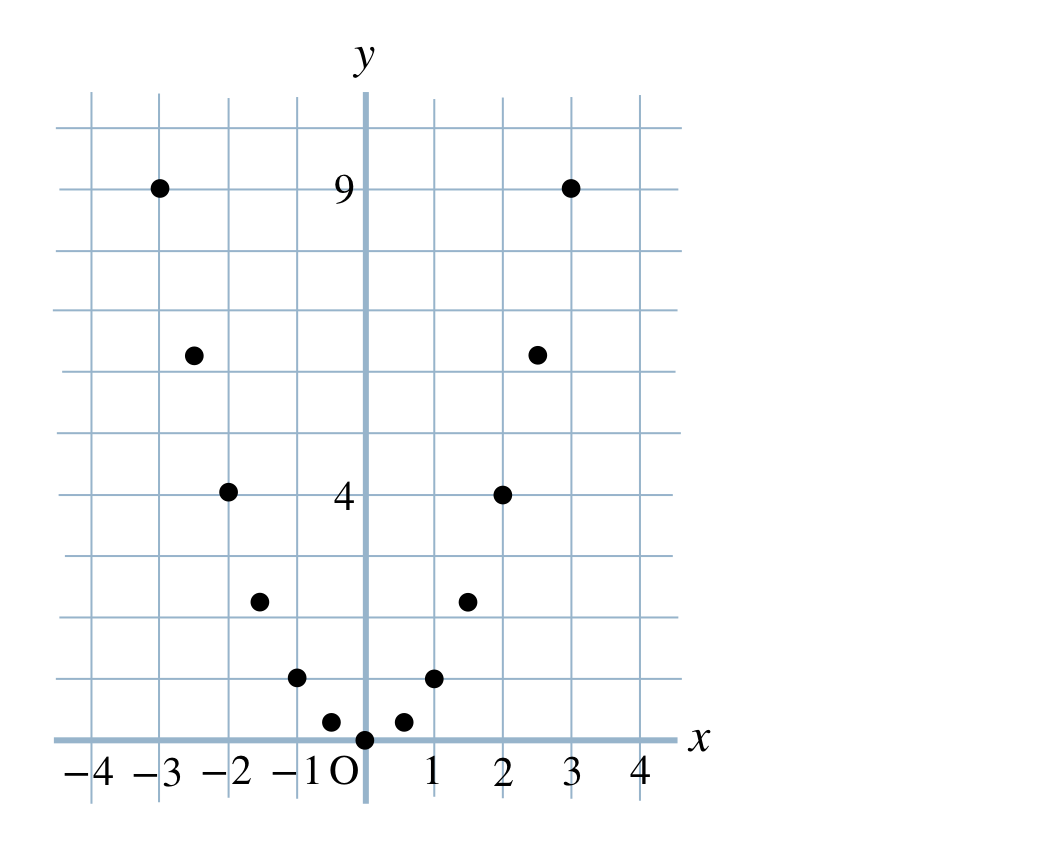

■ 同じタイプの例題解説
» 関数y=ax²のグラフ
» 関数y=ax²のグラフ
p.95 問2\(\begin{split}&(-1~,~1)~,~(-0.9~,~0.81)\\[2pt]~~~&(-0.8~,~0.64)~,~(-0.7~,~0.49)\\[2pt]~~~&(-0.6~,~0.36)~,~(-0.5~,~0.25)\\[2pt]~~~&(-0.4~,~0.16)~,~(-0.3~,~0.09)\\[2pt]~~~&(-0.2~,~0.04)~,~(-0.1~,~0.01)\\[2pt]~~~&(0~,~0)~,~(0.1~,~0.01)\\[2pt]~~~&(0.2~,~0.04)~,~(0.3~,~0.09)\\[2pt]~~~&(0.4~,~0.16)~,~(0.5~,~0.25)\\[2pt]~~~&(0.6~,~0.36)~,~(0.7~,~0.49)\\[2pt]~~~&(0.8~,~0.64)~,~(0.9~,~0.81)\\[2pt]~~~&(1~,~1)\end{split}\)
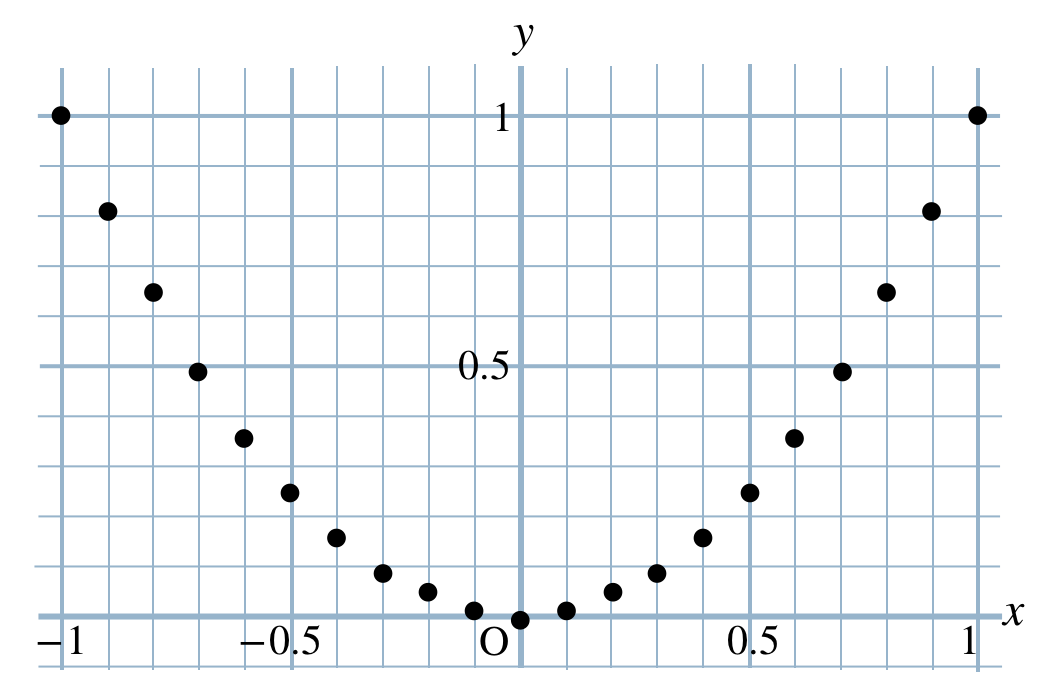

■ 同じタイプの例題解説
» 関数y=ax²のグラフ
» 関数y=ax²のグラフ
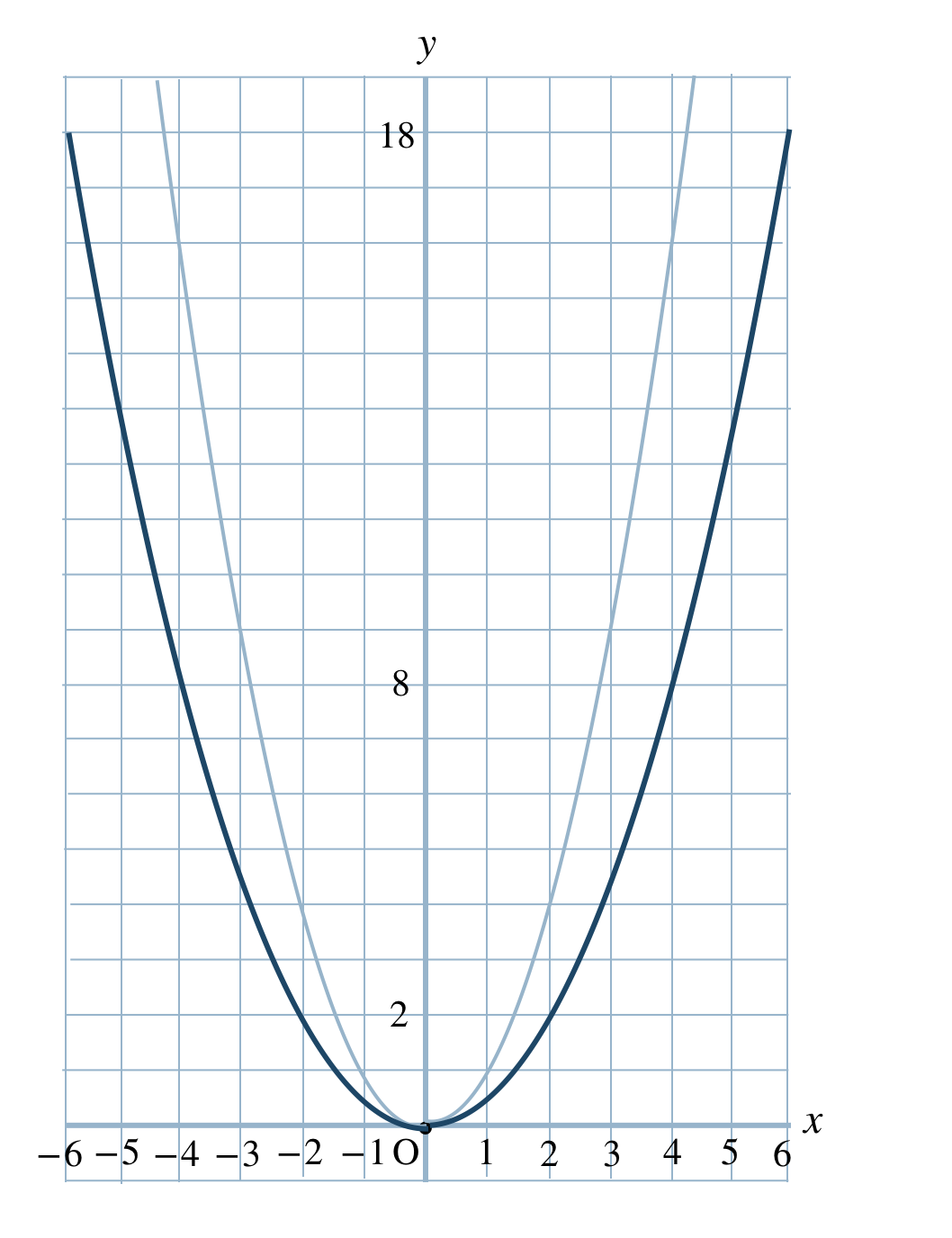
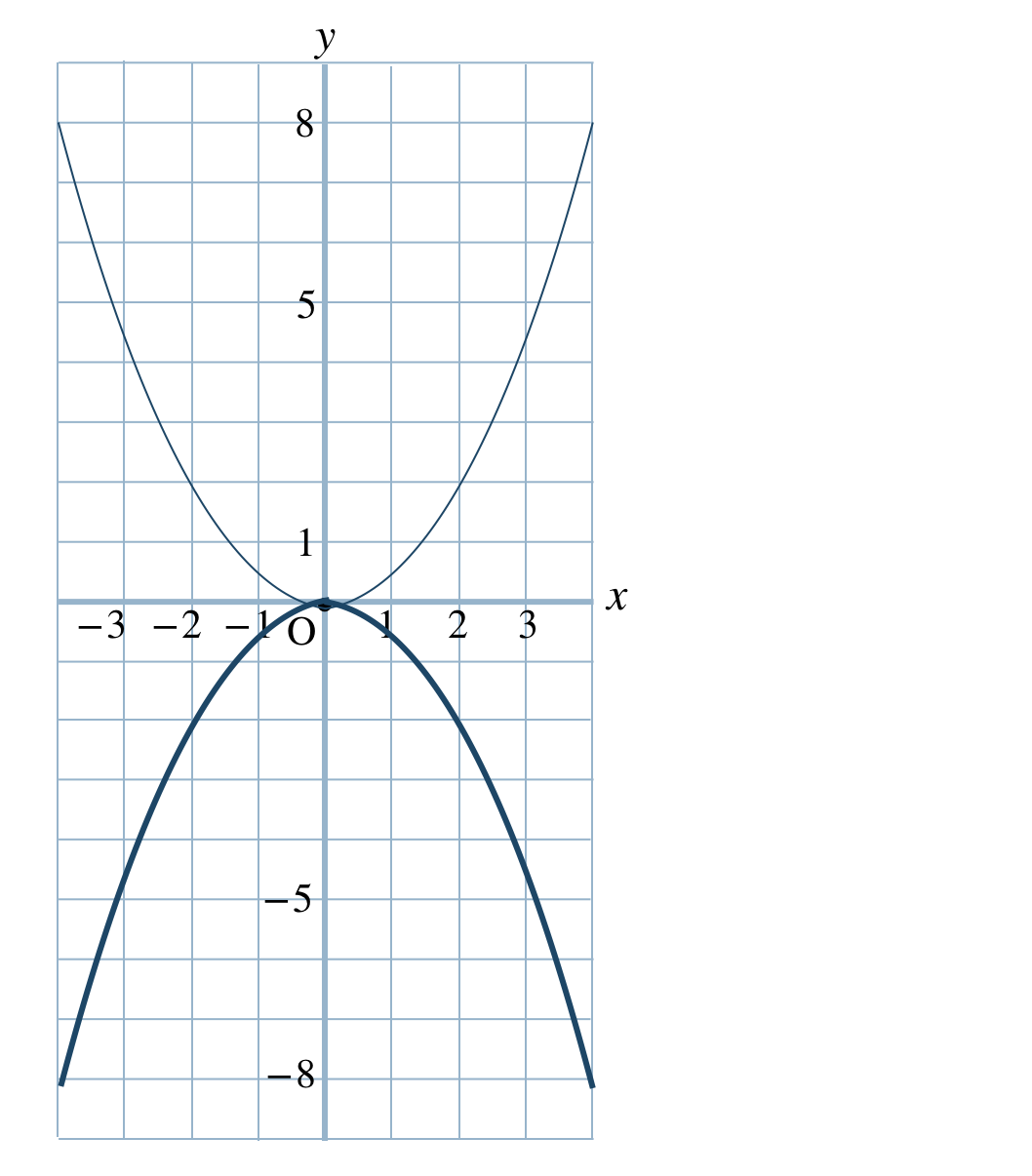
p.101 説明しよう ① \(\begin{split}y=3x^2\end{split}\) ② \(\begin{split}y=\frac{\,1\,}{\,4\,}x^2\end{split}\)
③ \(\begin{split}y=-x^2\end{split}\)
①と②は上に開いているグラフで、①の方が開き方が小さいので、比例定数の絶対値が大きい。
③は下に開いたグラフとなる。
③ \(\begin{split}y=-x^2\end{split}\)
①と②は上に開いているグラフで、①の方が開き方が小さいので、比例定数の絶対値が大きい。
③は下に開いたグラフとなる。
■ 同じタイプの例題解説
» 関数y=ax²のグラフ
» 関数y=ax²のグラフ
2節 関数y=ax²の値の変化
1 関数y=ax²の値の増減と変域
p.105 問1\(\begin{split}{\small (1)}~0≦y≦8\end{split}\) \(\begin{split}{\small (2)}~2≦y≦8\end{split}\)
■ 同じタイプの例題解説
» 関数y=ax²と変域
» 関数y=ax²と変域
p.105 問2\(\begin{split}{\small (1)}~-4≦y≦-1\end{split}\) \(\begin{split}{\small (2)}~-4≦y≦0\end{split}\)
■ 同じタイプの例題解説
» 関数y=ax²と変域
» 関数y=ax²と変域
2 関数y=ax²の値の変化の割合
p.107 問1\(\begin{split}{\small (1)}~10\end{split}\) \(\begin{split}{\small (2)}~-10\end{split}\)
■ 同じタイプの例題解説
» 関数y=ax²の変化の割合
» 関数y=ax²の変化の割合
p.107 問2\(\begin{split}{\small (1)}~-4\end{split}\) \(\begin{split}{\small (2)}~6\end{split}\)
■ 同じタイプの例題解説
» 関数y=ax²の変化の割合
» 関数y=ax²の変化の割合
p.109 問3\({\small (1)}~\)毎秒 \(6~{\rm m}\) \({\small (2)}~\)毎秒 \(16~{\rm m}\)
■ 同じタイプの例題解説
» 関数y=ax²と平均の速さ
» 関数y=ax²と平均の速さ
p.109 まとめよう 直線、放物線
減少、増加
\(a\)
減少、増加
\(a\)
3節 いろいろな事象と関数
1 関数y=ax²の利用
p.111 問1\(\begin{split}~~~y=\frac{\,3\,}{\,500\,}x^2\end{split}\)
■ 同じタイプの例題解説
» 関数y=ax²と制動距離
» 関数y=ax²と制動距離
p.111 問2\(\begin{split}~~~60~{\rm m}\end{split}\)
■ 同じタイプの例題解説
» 関数y=ax²と制動距離
» 関数y=ax²と制動距離
p.111 説明しよう時速 \(30~{\rm km}\) と時速 \(40~{\rm km}\) のときの制動距離の差は \(4.2~{\rm m}\) 。
時速 \(50~{\rm km}\) と時速 \(60~{\rm km}\) のときの制動距離の差は \(6.6~{\rm m}\) 。
よって、速さが早くなるほど制動距離の長さの変化も大きくなる。
時速 \(50~{\rm km}\) と時速 \(60~{\rm km}\) のときの制動距離の差は \(6.6~{\rm m}\) 。
よって、速さが早くなるほど制動距離の長さの変化も大きくなる。
■ 同じタイプの例題解説
» 関数y=ax²と制動距離
» 関数y=ax²と制動距離
p.112 問3\(\begin{split}~~~\frac{\,1\,}{\,4\,}~{\rm m}\end{split}\)
■ 同じタイプの例題解説
» 関数y=ax²と図形
» 関数y=ax²と図形
p.112 問4\({\small (1)}~\)\(2\) 秒 \({\small (2)}~\)\(4\) 秒
■ 同じタイプの例題解説
» 関数y=ax²と図形
» 関数y=ax²と図形
p.113 問5\(\begin{split}{\small (1)}~y=2x^2~~(0≦x≦4)\end{split}\)
\(\begin{split}{\small (2)}~\end{split}\)
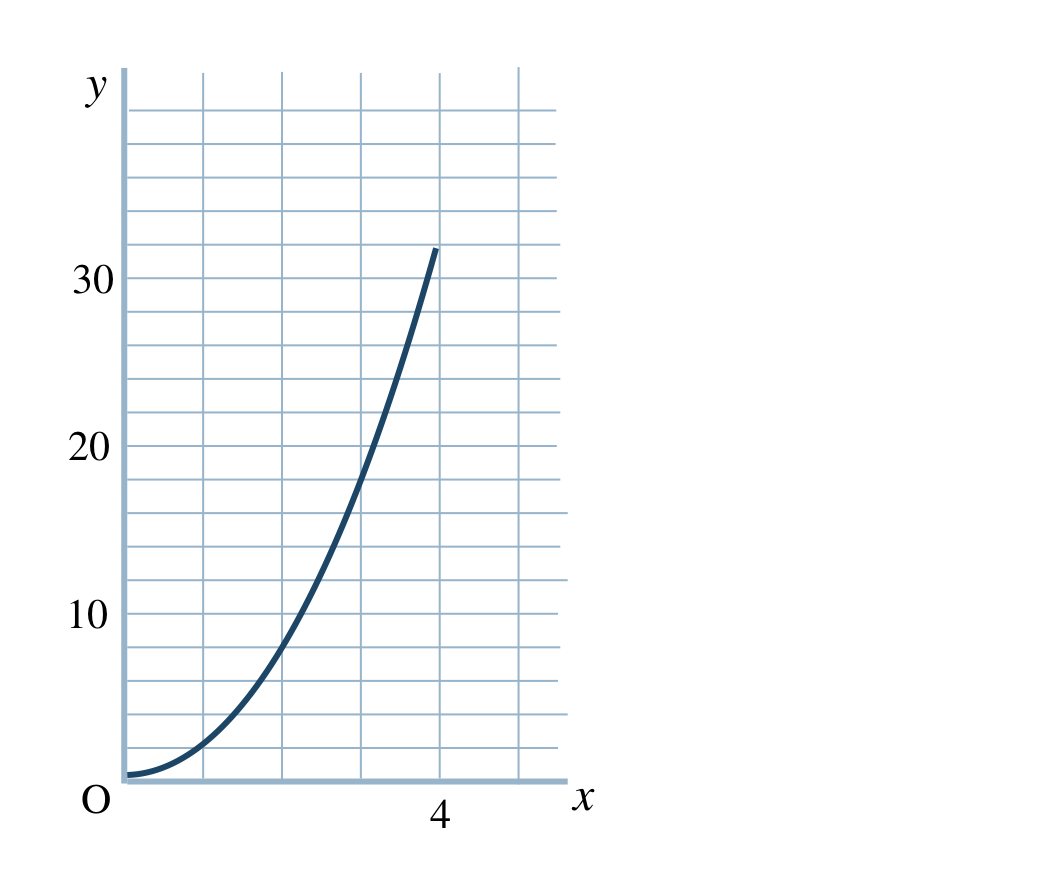
\(\begin{split}{\small (3)}~\end{split}\)\(2\sqrt{2}\) 秒後
\(\begin{split}{\small (2)}~\end{split}\)

\(\begin{split}{\small (3)}~\end{split}\)\(2\sqrt{2}\) 秒後
■ 同じタイプの例題解説
» 関数y=ax²と図形
» 関数y=ax²と図形
2 いろいろな関数
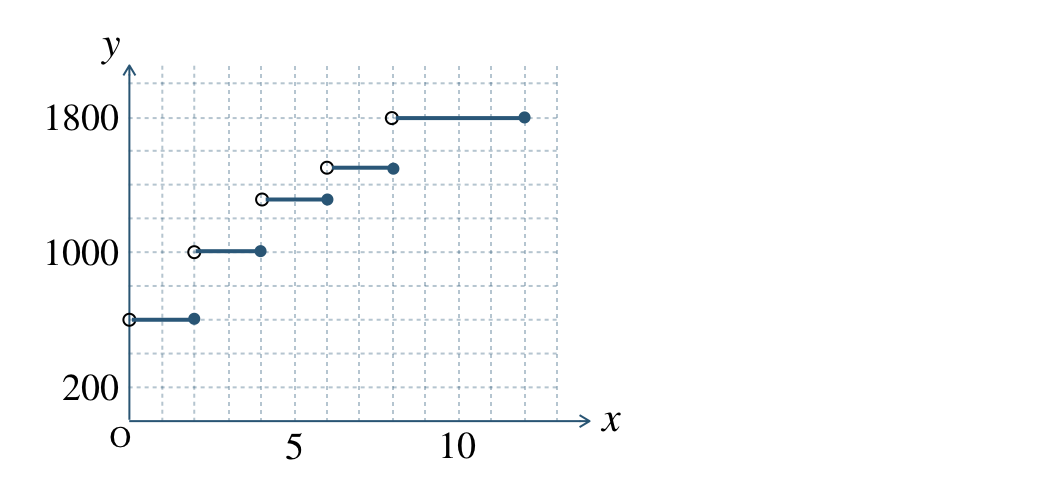
p.114 問1\(\begin{split}~~~2<x≦4\end{split}\) \(\begin{split}~~~4<x≦6\end{split}\)
\(\begin{split}~~~y=1500\end{split}\)
\(\begin{split}~~~y=1500\end{split}\)
■ 同じタイプの例題解説
» いろいろな関数
» いろいろな関数
p.115 話しあおう \(2\) 時間まではA店
\(2\) 時間から \(4\) 時間まではB店
\(4\) 時間から \(8\) 時間まではA店
\(8\) 時間から \(12\) 時間まではB店
\(2\) 時間から \(4\) 時間まではB店
\(4\) 時間から \(8\) 時間まではA店
\(8\) 時間から \(12\) 時間まではB店
■ 同じタイプの例題解説
» いろいろな関数
» いろいろな関数
p.115 説明しよう エ
■ 同じタイプの例題解説
» いろいろな関数
» いろいろな関数
次のページ「5章 図形と相似」