数研出版：これからの数学２

p.107 問1\(\angle a+\angle b=180^\circ\) より、
　\(\angle a=180^\circ-\angle b\)
また、\(\angle b+\angle c=180^\circ\) より、
　\(\angle c=180^\circ-\angle b\)
ともに \(180^\circ-\angle b\) であるので、
　\(\angle a=\angle c\)

p.107 問2\(\begin{split}~~~\angle a=35^\circ~,~\angle b=85^\circ\end{split}\)
\(\begin{split}~~~\angle c=60^\circ~,~\angle d=60^\circ\end{split}\)

p.108 問3\(\begin{split}{\small (1)}~\angle w\end{split}\)　　\(\begin{split}{\small (2)}~\angle t\end{split}\)

p.108 問4\(\begin{split}~~~\angle x=60^\circ~,~\angle y=70^\circ\end{split}\)

p.110 問5　\(l\,//\,n\)、同位角が等しい

p.111 問6　\(c\)、\(c\)、同位角

p.111 問7\({\small (1)}~\)錯角が等しい
\({\small (2)}~\angle x=80^\circ~,~\angle y=50^\circ\)

p.111 問8\(l\,//\,m\) より、同位角が等しいから
　\(\angle a=\angle b~~~\cdots{\large ①}\)
また、\(l\,//\,n\) より、同位角が等しいから
　\(\angle a=\angle c~~~\cdots{\large ②}\)
①、②より、
　\(\angle b=\angle c\)
よって、同位角が等しいから、
　\(m\,//\,n\)

p.113 問1\(\begin{split}~~~\angle d+\angle e\end{split}\)

p.113 問2\(\begin{split}{\small (1)}~\angle x=65^\circ\end{split}\)　　\(\begin{split}{\small (2)}~\angle x=100^\circ\end{split}\)
\(\begin{split}{\small (3)}~\angle x=110^\circ\end{split}\)

p.115 問3\(\begin{split}{\small (1)}~\angle x=80^\circ\end{split}\)　　\(\begin{split}{\small (2)}~\angle x=35^\circ\end{split}\)

p.115 問4３つの内角のうち２つがともに直角や鈍角とすると、
その２つの角の和が \(180^\circ\) より大きくなり、三角形の内角の和が \(180^\circ\) とならない

p.115 問5\({\small (1)}~\)直角三角形　　\({\small (2)}~\)鈍角三角形
\({\small (3)}~\)鋭角三角形

p.116 問6\(\begin{split}{\small (1)}~\angle x=70^\circ\end{split}\)　　\(\begin{split}{\small (2)}~\angle x=150^\circ\end{split}\)

p.118 問1かんなさん \(180^\circ\times(n-1)-180^\circ\)
ひびきさん \(180^\circ\times n-360^\circ\)

p.118 問2\({\small (1)}~1800^\circ\)　　\({\small (2)}~160^\circ\)
\({\small (3)}~\)九角形

p.120 問3\(\begin{split}{\small (1)}~\angle x=105^\circ\end{split}\)　　\(\begin{split}{\small (2)}~\angle x=80^\circ\end{split}\)
\(\begin{split}{\small (3)}~\angle x=45^\circ\end{split}\)

p.121 問4\({\small (1)}~30^\circ\)　　\({\small (2)}~\)正八角形

p.123 問1\(\begin{split}~~~\triangle {\rm ABD}\equiv\triangle {\rm CBD}\end{split}\)

p.123 問2\(\begin{split}{\small (1)}~{\rm AB=CB}\end{split}\)　　\(\begin{split}{\small (2)}~\angle {\rm C}=\angle {\rm A}\end{split}\)
\(\begin{split}{\small (3)}~{\rm AD=CD}\end{split}\)　　\(\begin{split}{\small (4)}~\angle {\rm ADB}=\angle {\rm CDB}\end{split}\)

p.123 問3\(\begin{split}{\small (1)}~4~{\rm cm}\end{split}\)　　\(\begin{split}{\small (2)}~120^\circ\end{split}\)
\(\begin{split}{\small (3)}~90^\circ\end{split}\)

p.125 問1\({\small (1)}~\)

\({\small (2)}~\)

p.127 問2\(\triangle {\rm ABC}\equiv\triangle {\rm OMN}\)
２組の辺とその間の角がそれぞれ等しい

---

\(\triangle {\rm DEF}\equiv\triangle {\rm RQP}\)
３組の辺がそれぞれ等しい

---

\(\triangle {\rm GHI}\equiv\triangle {\rm LJK}\)
１組の辺とその両端の角がそれぞれ等しい

p.127 問3\({\small (1)}~\)\(\triangle {\rm ABD}\equiv\triangle {\rm CBD}\)
３組の辺がそれぞれ等しい

---

\({\small (2)}~\)\(\triangle {\rm ACO}\equiv\triangle {\rm BDO}\)
１組の辺とその両端の角がそれぞれ等しい

---

\({\small (3)}~\)\(\triangle {\rm AOC}\equiv\triangle {\rm BOD}\)
２組の辺とその間の角がそれぞれ等しい

p.127 問4\({\small (1)}~\)いえない

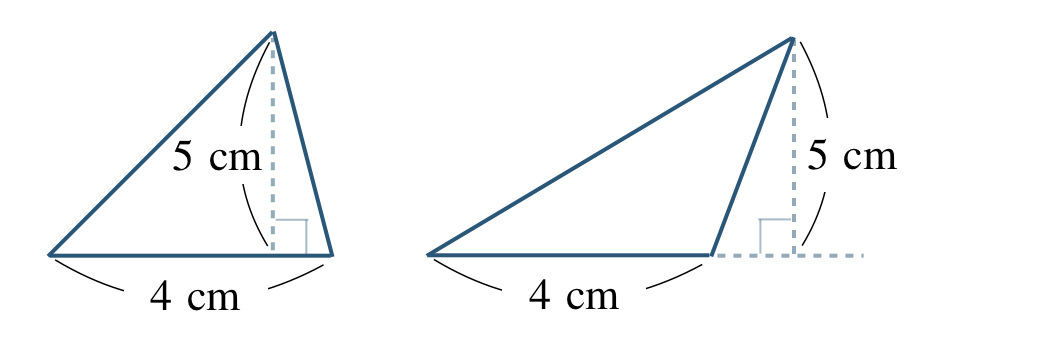
(３組の角が等しいときでも、３組の辺の長さが違う場合がある。)

---

\({\small (2)}~\)いえる

---

\({\small (3)}~\)いえない

p.128 問1\({\small (1)}~\)仮定：\(l\,//\,m\)
　　結論：\(\angle a=\angle b\)
\({\small (2)}~\)仮定：\({\rm AB=CB~,~AD=CD}\)
　　結論：\(\triangle {\rm ABD}\equiv\triangle {\rm CBD}\)

p.133 問2④の根拠は、
　３組の辺がそれぞれ等しい
⑤の根拠は、
　合同な図形では対応する角の大きさは等しい

p.134 問3\({\small (1)}~\)仮定：\({\rm AP=BP~,~CP=DP}\)
　　結論：\({\rm AC\,//\,DB}\)
\({\small (2)}~\)
ア：対頂角は等しいから
イ：\(\angle {\rm BPD}\)
ウ：２組の辺とその間の角がそれぞれ等しい
エ：対応する角の大きさは等しい
オ：\(\angle {\rm BDP}\)
カ：錯角が等しい

p.134 問4[証明] \(\triangle {\rm ABC}\) と \(\triangle {\rm ABC}\) において、
仮定から、
　\({\rm AB=CD}~~~\cdots{\large ①}\)
　\({\rm \angle ABD=\angle CDB}~~~\cdots{\large ②}\)
共通な辺であるから、
　\({\rm BD=DB}~~~\cdots{\large ③}\)
①、②、③より、
２組の辺とその間の角がそれぞれ等しいから
　\(\triangle {\rm ABD}\equiv\triangle {\rm CDB}\)
合同な図形では対応する角の大きさは等しいから
　\({\rm \angle ADB=\angle CBD}\)
錯角が等しいから
　\({\rm AD\,//\,BC}\) [終]