このページは、数研出版：これからの数学２
３章 １次関数
３章 １次関数
教科書に完全対応の問題集｜教科書ぴったりトレーニング
教科書に対応した数学の問題集｜教科書ぴったりトレーニングの紹介 こんにちは、みなさん！今回は中学生の...
jhs.yorikuwa.com
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
数研出版中２ １章 式の計算
数研出版中２ ２章 連立方程式
数研出版中２ ３章 １次関数
数研出版中２ ４章 図形の性質と合同
数研出版中２ ５章 三角形と四角形
数研出版中２ ６章 データの活用
数研出版中２ ７章 確率
３章 １次関数
１ １次関数
１ １次関数
p.70 問1\(\begin{split}~~~5~,~7~,~9~,~11~,~13\end{split}\)
■ 同じタイプの例題解説
» １次関数の式
» １次関数の式
p.71 問2\({\small (1)}~23~{\rm cm}\) \({\small (2)}~21~\)分後
■ 同じタイプの例題解説
» １次関数の式
» １次関数の式
p.71 問3\(\begin{split}~~~y=-2x+30\end{split}\)
■ 同じタイプの例題解説
» １次関数の式
» １次関数の式
p.72 問4\(\begin{split}~~~4.8~{\rm cm}\end{split}\)
■ 同じタイプの例題解説
» １次関数の式
» １次関数の式
p.72 問5
ア： \(y=-x+248\) イ： \(\begin{split}y={\frac{\,10\,}{\,x\,}}\end{split}\)
ウ： \(y=5x\)
１次関数であるものはア、ウ
ア： \(y=-x+248\) イ： \(\begin{split}y={\frac{\,10\,}{\,x\,}}\end{split}\)
ウ： \(y=5x\)
１次関数であるものはア、ウ
■ 同じタイプの例題解説
» １次関数の式
» １次関数の式
２ １次関数の値の変化
p.74 問1\({\small (1)}~y\) の増加量 \(12\)、変化の割合 \(4\)
\({\small (2)}~y\) の増加量 \(-9\)、変化の割合 \(-3\)
\({\small (2)}~y\) の増加量 \(-9\)、変化の割合 \(-3\)
■ 同じタイプの例題解説
» １次関数の変化の割合
» １次関数の変化の割合
p.74 問2\({\small (1)}~\) 変化の割合 \(3\)、\(y\)の増加量 \(6\)
\({\small (2)}~\) 変化の割合 \(-5\)、\(y\)の増加量 \(-10\)
\({\small (3)}~\) 変化の割合 \(\begin{split}-{\frac{\,1\,}{\,2\,}}\end{split}\)、\(y\)の増加量 \(-1\)
\({\small (2)}~\) 変化の割合 \(-5\)、\(y\)の増加量 \(-10\)
\({\small (3)}~\) 変化の割合 \(\begin{split}-{\frac{\,1\,}{\,2\,}}\end{split}\)、\(y\)の増加量 \(-1\)
■ 同じタイプの例題解説
» １次関数の変化の割合
» １次関数の変化の割合
p.74 問3
\(\begin{split}{\small (1)}~-\frac{\,1\,}{\,2\,}\end{split}\) \(\begin{split}{\small (2)}~-2\end{split}\)
\(\begin{split}{\small (1)}~-\frac{\,1\,}{\,2\,}\end{split}\) \(\begin{split}{\small (2)}~-2\end{split}\)
■ 同じタイプの例題解説
» １次関数の変化の割合
» １次関数の変化の割合
３ １次関数のグラフ
p.75 問1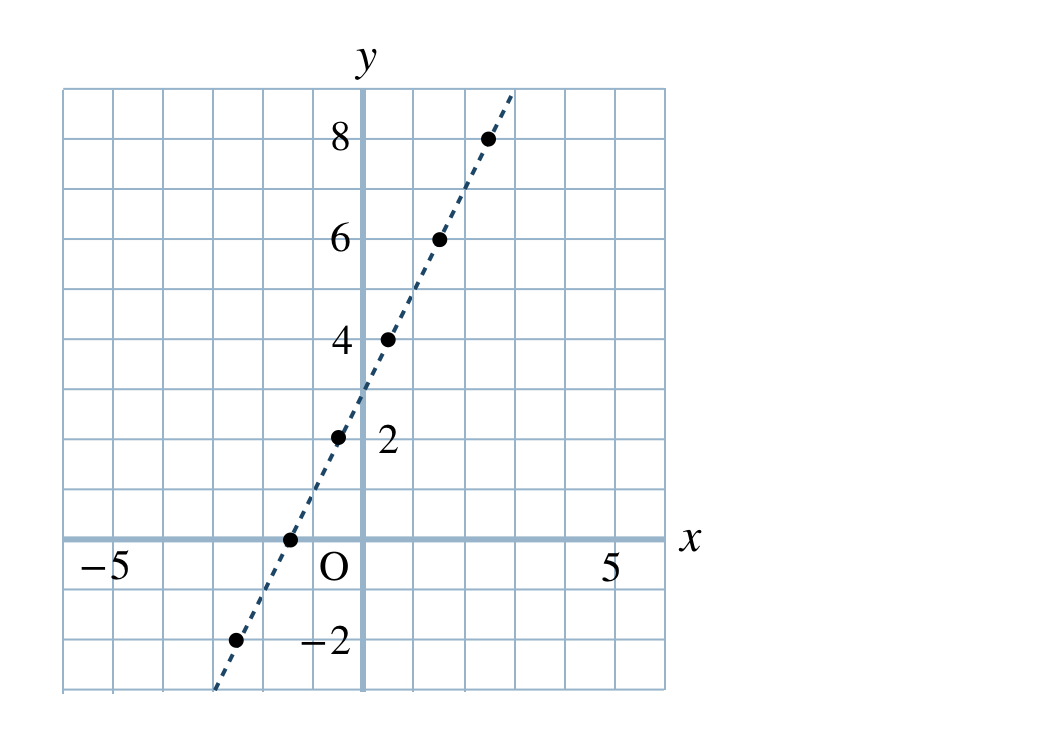
点全体は直線となる
点全体は直線となる
p.77 問2\({\small (1)}~\)\(y\) 軸の正の方向に \(+1\)
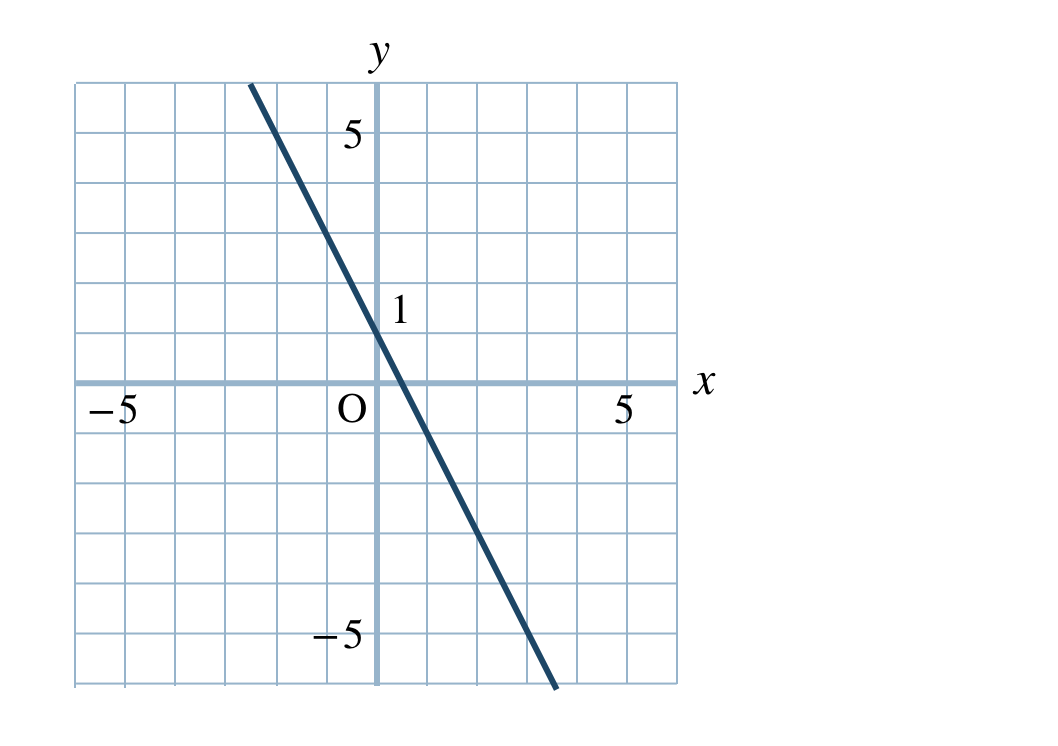
\({\small (2)}~\)\(y\) 軸の正の方向に \(-3\)
\({\small (2)}~\)\(y\) 軸の正の方向に \(-3\)
■ 同じタイプの例題解説
» １次関数のグラフと切片
» １次関数のグラフと切片
p.77 問3\({\small (1)}~\)③のグラフを \(y\) 軸の正の方向に \(+1\)
\({\small (2)}~\)①のグラフを \(y\) 軸の正の方向に \(-2\)
\({\small (3)}~\)②のグラフを \(y\) 軸の正の方向に \(\begin{split}-{\frac{\,3\,}{\,4\,}}\end{split}\)
\({\small (2)}~\)①のグラフを \(y\) 軸の正の方向に \(-2\)
\({\small (3)}~\)②のグラフを \(y\) 軸の正の方向に \(\begin{split}-{\frac{\,3\,}{\,4\,}}\end{split}\)
■ 同じタイプの例題解説
» １次関数のグラフと切片
» １次関数のグラフと切片
p.77 問4
\(\begin{split}{\small (1)}~3\end{split}\) \(\begin{split}{\small (2)}~0\end{split}\) \(\begin{split}{\small (3)}~-\frac{\,1\,}{\,4\,}\end{split}\)
\(\begin{split}{\small (1)}~3\end{split}\) \(\begin{split}{\small (2)}~0\end{split}\) \(\begin{split}{\small (3)}~-\frac{\,1\,}{\,4\,}\end{split}\)
■ 同じタイプの例題解説
» １次関数のグラフと切片
» １次関数のグラフと切片
p.78 問5\({\small (1)}~\)右へ \(1\) 進むとき上に \(1\) 進む
右へ \(2\) 進むとき上に \(2\) 進む
\({\small (2)}~\)右へ \(1\) 進むとき上に \(3\) 進む
右へ \(2\) 進むとき上に \(6\) 進む
右へ \(2\) 進むとき上に \(2\) 進む
\({\small (2)}~\)右へ \(1\) 進むとき上に \(3\) 進む
右へ \(2\) 進むとき上に \(6\) 進む
■ 同じタイプの例題解説
» １次関数のグラフと傾き
» １次関数のグラフと傾き
p.79 問6
\(\begin{split}{\small (1)}~2\end{split}\) \(\begin{split}{\small (2)}~-1\end{split}\) \(\begin{split}{\small (3)}~-\frac{\,2\,}{\,3\,}\end{split}\)
\(\begin{split}{\small (1)}~2\end{split}\) \(\begin{split}{\small (2)}~-1\end{split}\) \(\begin{split}{\small (3)}~-\frac{\,2\,}{\,3\,}\end{split}\)
■ 同じタイプの例題解説
» １次関数のグラフと傾き
» １次関数のグラフと傾き
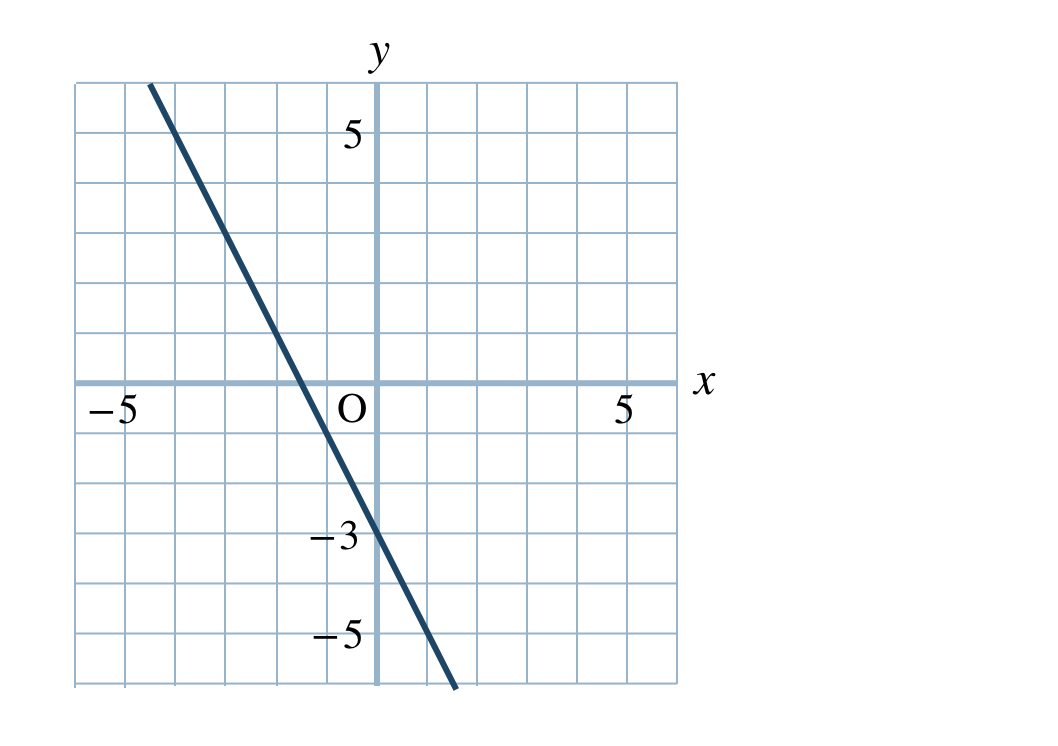
p.82 問7\(\begin{split}{\small (1)}~\end{split}\)
\(\begin{split}{\small (2)}~\end{split}\)
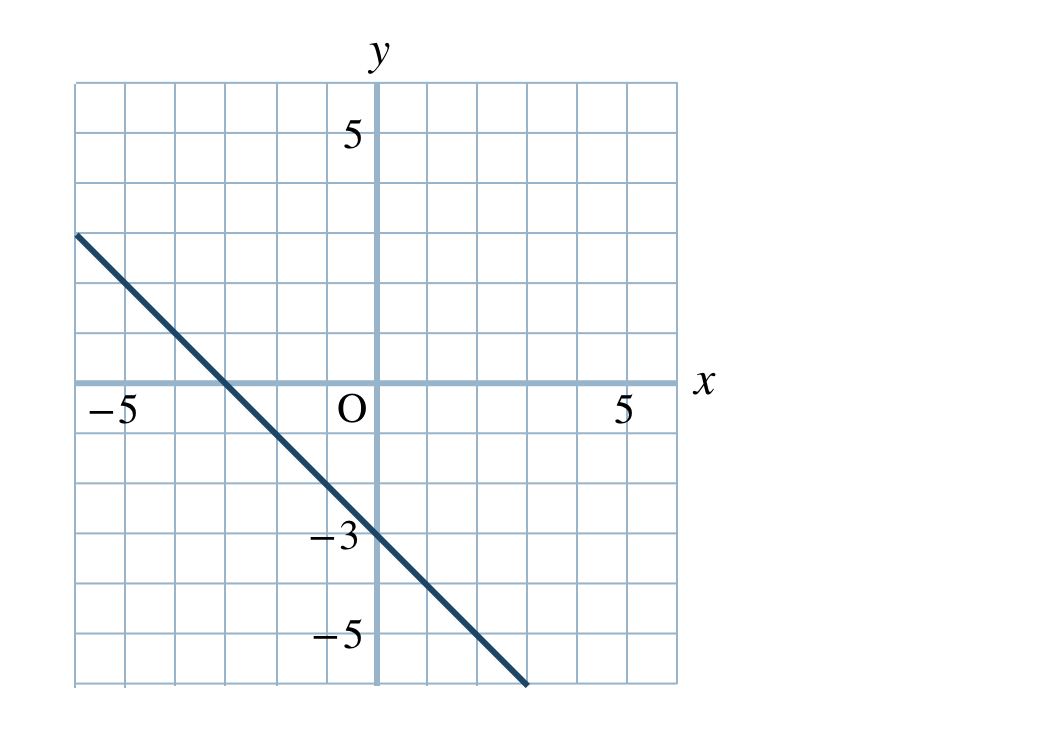
\(\begin{split}{\small (3)}~\end{split}\)
\(\begin{split}{\small (2)}~\end{split}\)
\(\begin{split}{\small (3)}~\end{split}\)
■ 同じタイプの例題解説
» １次関数のグラフのかき方
» １次関数のグラフのかき方
p.82 問8\(\begin{split}{\small (1)}~\end{split}\)
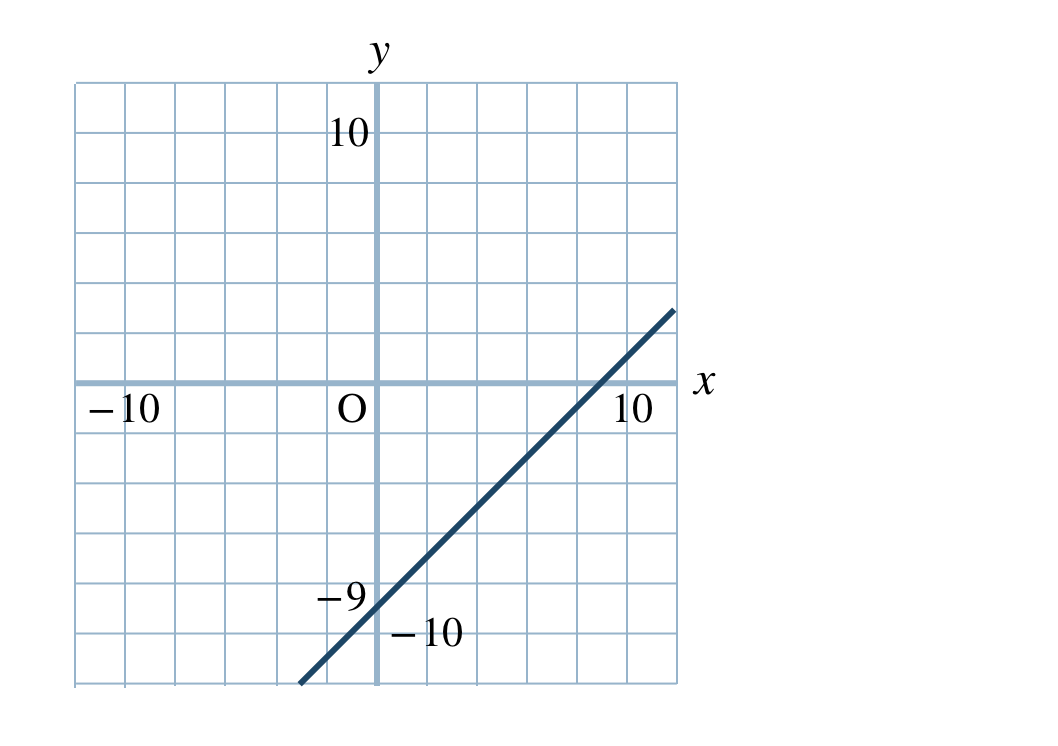
\(\begin{split}{\small (2)}~\end{split}\)
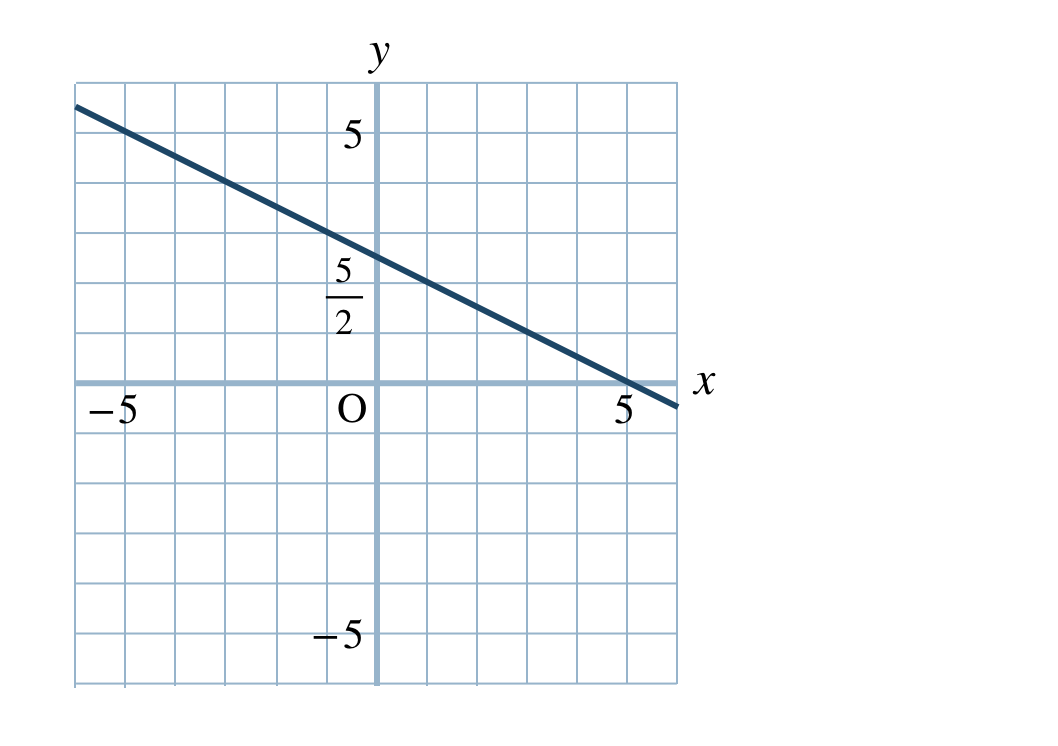
\(\begin{split}{\small (2)}~\end{split}\)
■ 同じタイプの例題解説
» １次関数のグラフのかき方
» １次関数のグラフのかき方
p.83 問9\(\begin{split}{\small (1)}~-5< y ≦ 5\end{split}\)
\(\begin{split}{\small (2)}~y< 4\end{split}\)
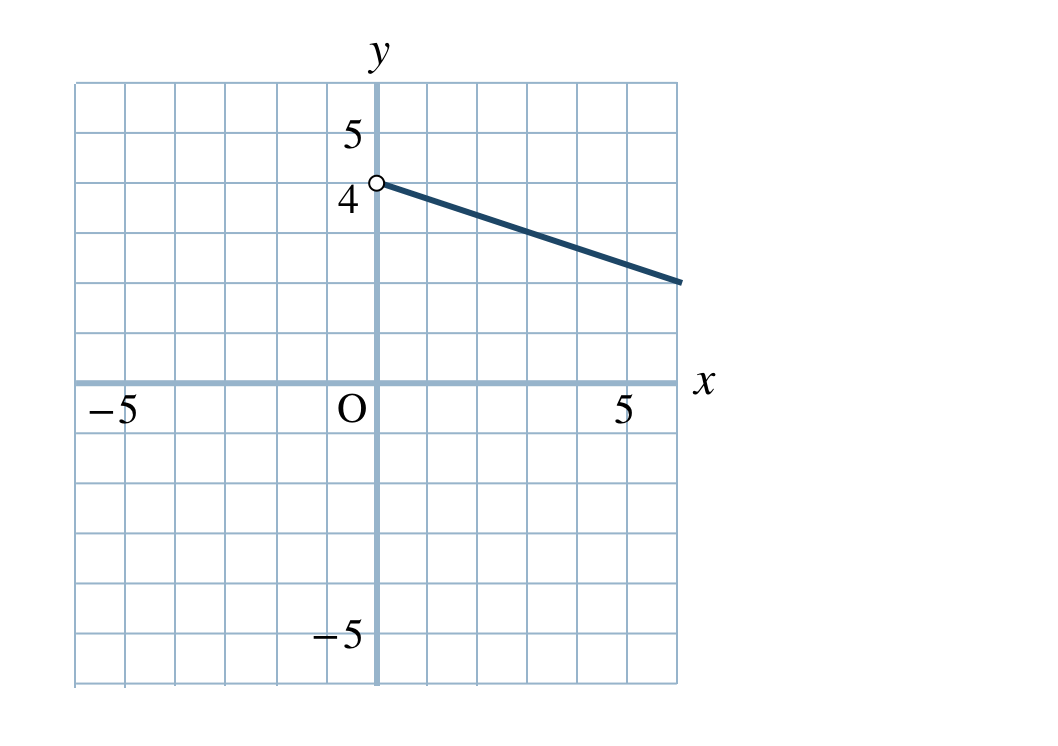
\(\begin{split}{\small (2)}~y< 4\end{split}\)
■ 同じタイプの例題解説
» １次関数のグラフの変域
» １次関数のグラフの変域
４ １次関数の式の求め方
p.84 問1\(\begin{split}{\small (1)}~y=x+1\end{split}\)
\(\begin{split}{\small (2)}~y=-2x+3\end{split}\)
\(\begin{split}{\small (3)}~y=\frac{\,3\,}{\,4\,}x+2\end{split}\)
\(\begin{split}{\small (2)}~y=-2x+3\end{split}\)
\(\begin{split}{\small (3)}~y=\frac{\,3\,}{\,4\,}x+2\end{split}\)
■ 同じタイプの例題解説
» グラフから１次関数の式を求める
» グラフから１次関数の式を求める
p.85 問2\(\begin{split}{\small (1)}~y=2x-9\end{split}\)
\(\begin{split}{\small (2)}~y=-3x+1\end{split}\)
\(\begin{split}{\small (3)}~y=\frac{\,1\,}{\,2\,}x+7\end{split}\)
\(\begin{split}{\small (2)}~y=-3x+1\end{split}\)
\(\begin{split}{\small (3)}~y=\frac{\,1\,}{\,2\,}x+7\end{split}\)
■ 同じタイプの例題解説
» １次関数の式と条件
» １次関数の式と条件
p.86 問3\(\begin{split}{\small (1)}~y=x-4\end{split}\)
\(\begin{split}{\small (2)}~y=-\frac{\,1\,}{\,2\,}x-1\end{split}\)
\(\begin{split}{\small (2)}~y=-\frac{\,1\,}{\,2\,}x-1\end{split}\)
■ 同じタイプの例題解説
» ２点を通る直線の式
» ２点を通る直線の式
２ １次関数と方程式
１ ２元１次方程式のグラフ
p.89 問1\(\begin{split}{\small (1)}~y=2x-2\end{split}\)
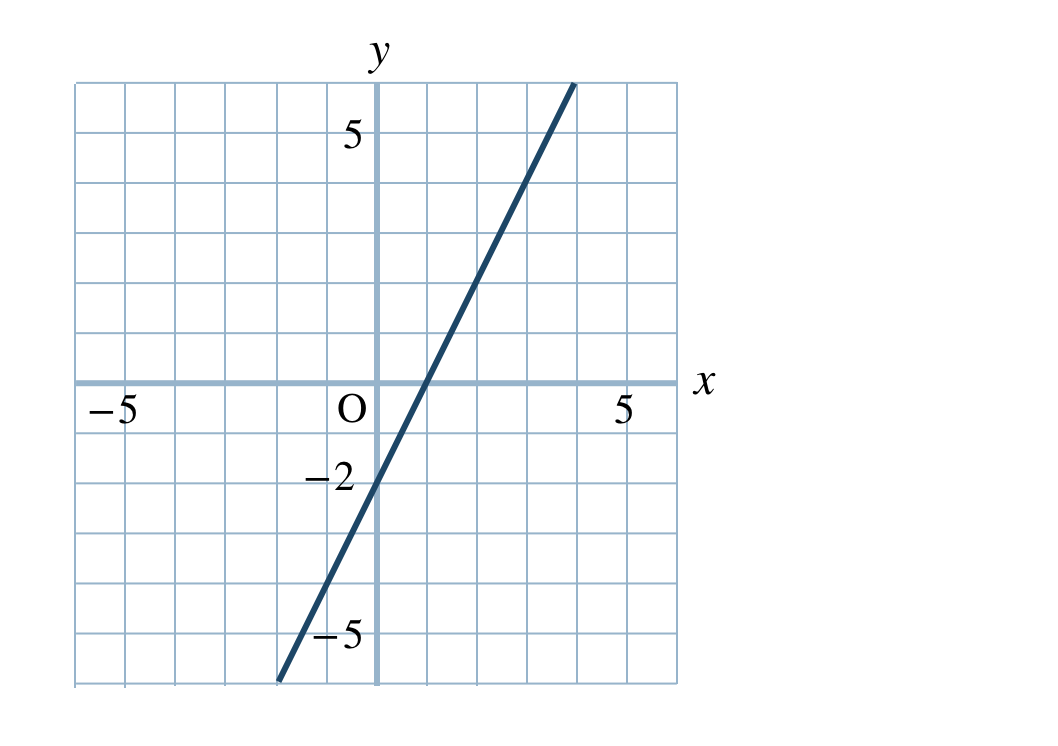
\(\begin{split}{\small (2)}~y=-\frac{\,3\,}{\,2\,}x+2\end{split}\)
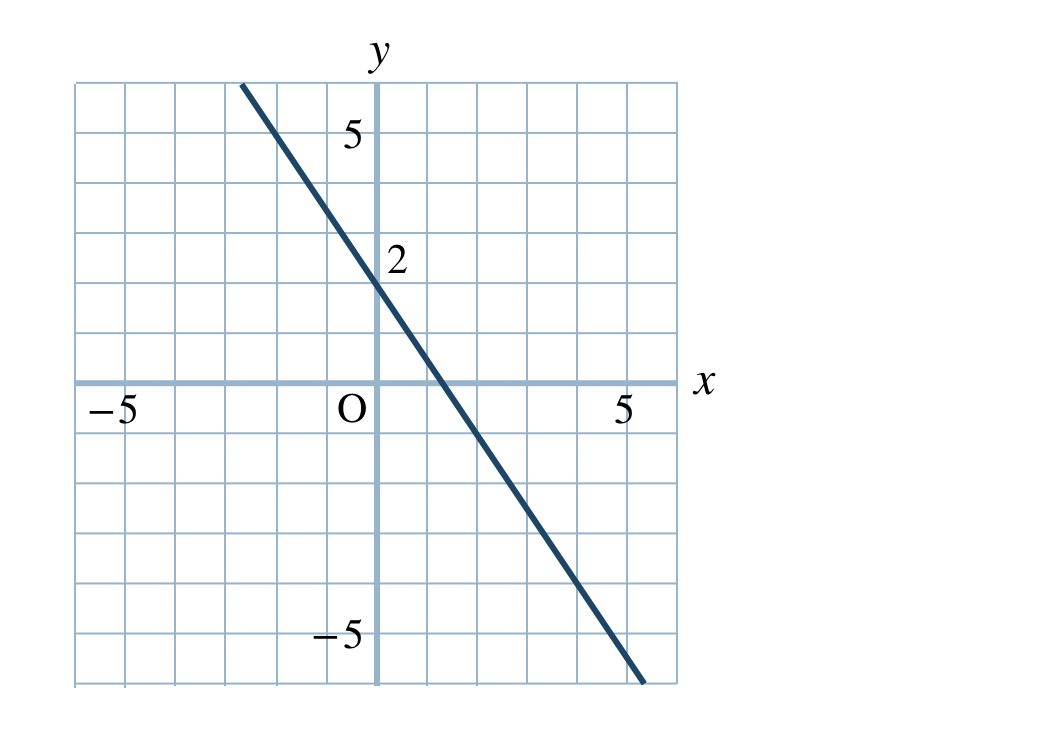
\(\begin{split}{\small (3)}~y=\frac{\,1\,}{\,3\,}x+1\end{split}\)
\(\begin{split}{\small (2)}~y=-\frac{\,3\,}{\,2\,}x+2\end{split}\)
\(\begin{split}{\small (3)}~y=\frac{\,1\,}{\,3\,}x+1\end{split}\)
■ 同じタイプの例題解説
» ２元１次方程式のグラフ
» ２元１次方程式のグラフ
p.90 問2\(\begin{split}~~~y=-\frac{\,2\,}{\,3\,}x+2\end{split}\)
■ 同じタイプの例題解説
» ２元１次方程式のグラフ
» ２元１次方程式のグラフ
p.90 問3\(\begin{split}{\small (1)}~y=\frac{\,2\,}{\,3\,}x-2\end{split}\)
\(\begin{split}{\small (2)}~y=-\frac{\,3\,}{\,4\,}x-3\end{split}\)
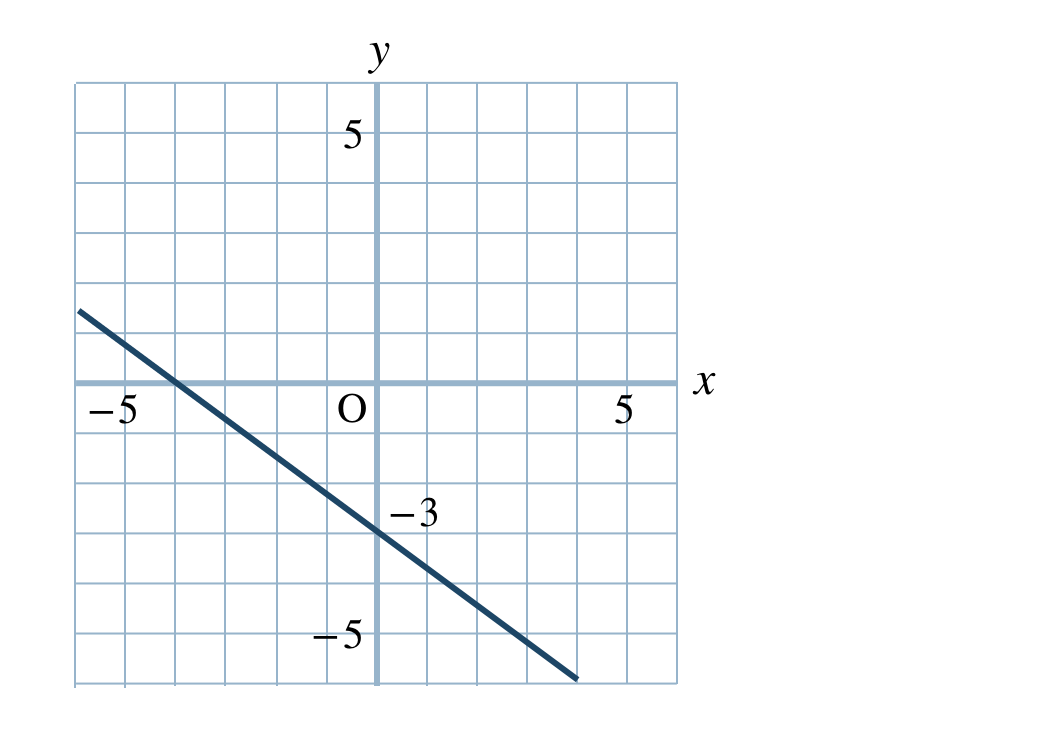
\(\begin{split}{\small (3)}~y=-\frac{\,2\,}{\,3\,}x+2\end{split}\)
\(\begin{split}{\small (2)}~y=-\frac{\,3\,}{\,4\,}x-3\end{split}\)
\(\begin{split}{\small (3)}~y=-\frac{\,2\,}{\,3\,}x+2\end{split}\)
■ 同じタイプの例題解説
» ２元１次方程式のグラフ
» ２元１次方程式のグラフ
p.91 問4\(\begin{split}{\small (1)}~y=2\end{split}\)
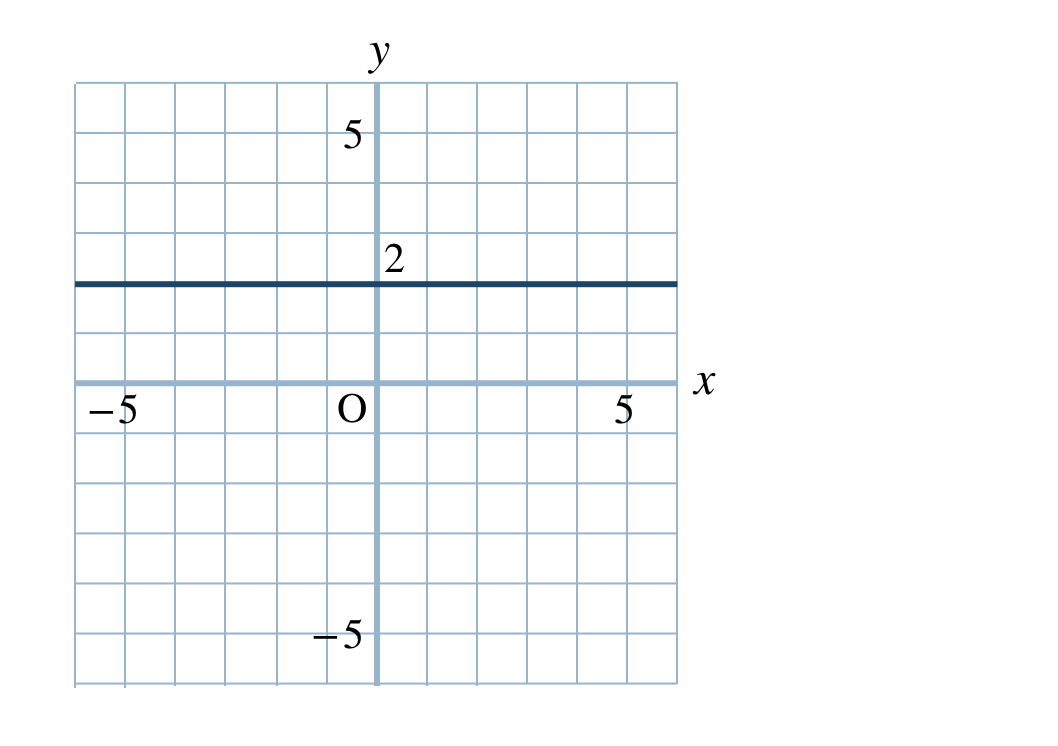
\(\begin{split}{\small (2)}~y=-2\end{split}\)
\(\begin{split}{\small (3)}~x=4\end{split}\)
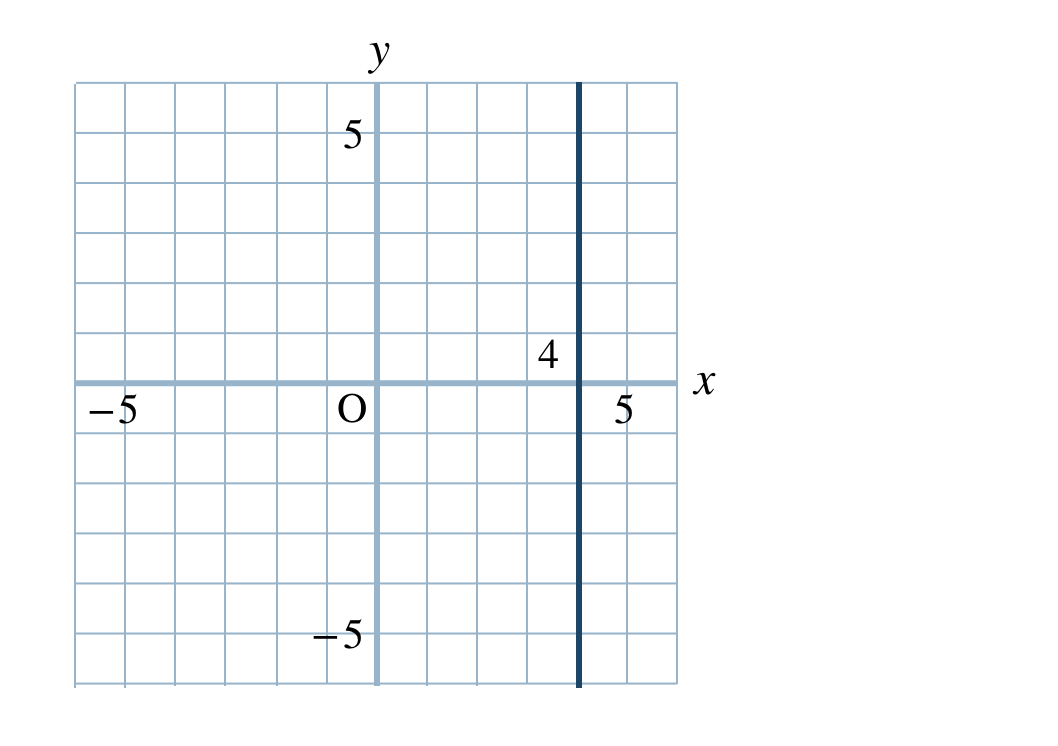
\(\begin{split}{\small (4)}~x=-3\end{split}\)
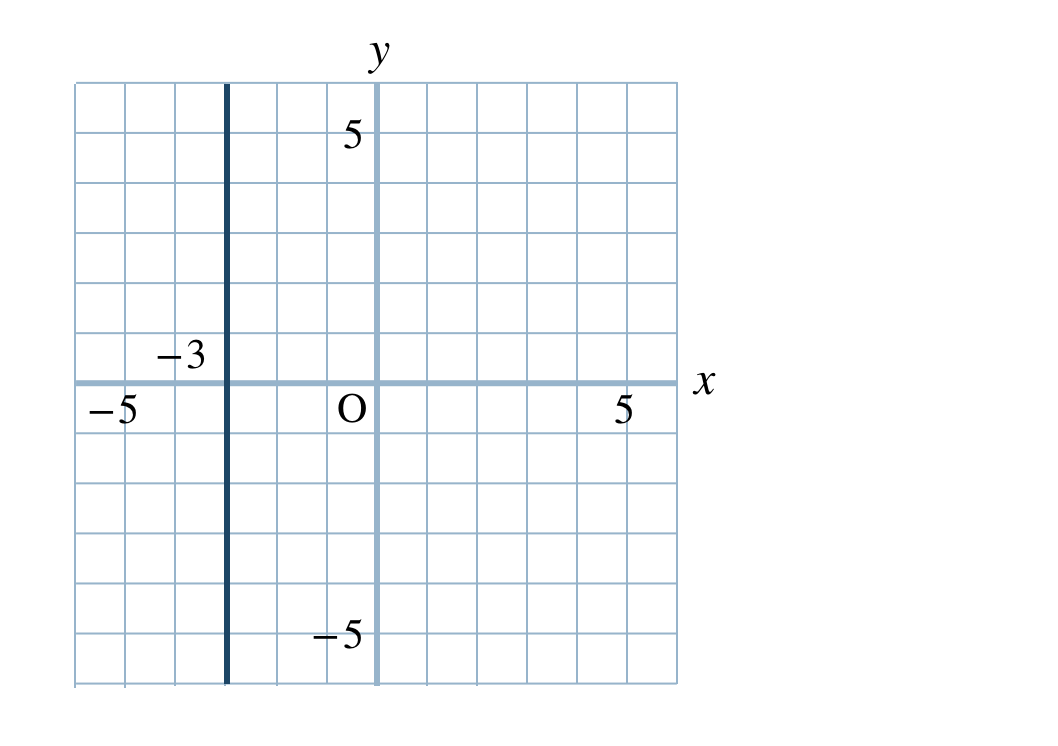
\(\begin{split}{\small (2)}~y=-2\end{split}\)
\(\begin{split}{\small (3)}~x=4\end{split}\)
\(\begin{split}{\small (4)}~x=-3\end{split}\)
■ 同じタイプの例題解説
» ２元１次方程式のグラフ
» ２元１次方程式のグラフ
２ 連立方程式とグラフ
p.92 問1\(\begin{split}{\small (1)}~x=-1~,~y=2\end{split}\)
\(\begin{split}{\small (2)}~x=\frac{\,4\,}{\,3\,}~,~y=-\frac{\,1\,}{\,3\,}\end{split}\)
\(\begin{split}{\small (2)}~x=\frac{\,4\,}{\,3\,}~,~y=-\frac{\,1\,}{\,3\,}\end{split}\)
■ 同じタイプの例題解説
» 連立方程式とグラフ
» 連立方程式とグラフ
p.93 問2
\(\begin{split}{\small (1)}~x=\frac{\,2\,}{\,3\,}~,~y=-\frac{\,5\,}{\,3\,}\end{split}\)
\(\begin{split}{\small (2)}~x=12~,~y=10\end{split}\)
\(\begin{split}{\small (1)}~x=\frac{\,2\,}{\,3\,}~,~y=-\frac{\,5\,}{\,3\,}\end{split}\)
\(\begin{split}{\small (2)}~x=12~,~y=10\end{split}\)
■ 同じタイプの例題解説
» 連立方程式とグラフ
» 連立方程式とグラフ
３ １次関数の利用
１ １次関数の利用
p.96 問1\({\small (1)}~76\) ℃ \({\small (2)}~\)およそ \(8\) 分後
p.97 問2\({\small (1)}~\)
\({\small (2)}~800~{\rm m}\)、8時16分 \({\small (3)}~\)郵便局の前
\({\small (2)}~800~{\rm m}\)、8時16分 \({\small (3)}~\)郵便局の前
■ 同じタイプの例題解説
» １次関数と道のり
» １次関数と道のり
p.98 問3\(\begin{split}~~~6≦x≦8\end{split}\)
\(\begin{split}~~~y=-2x+16\end{split}\)
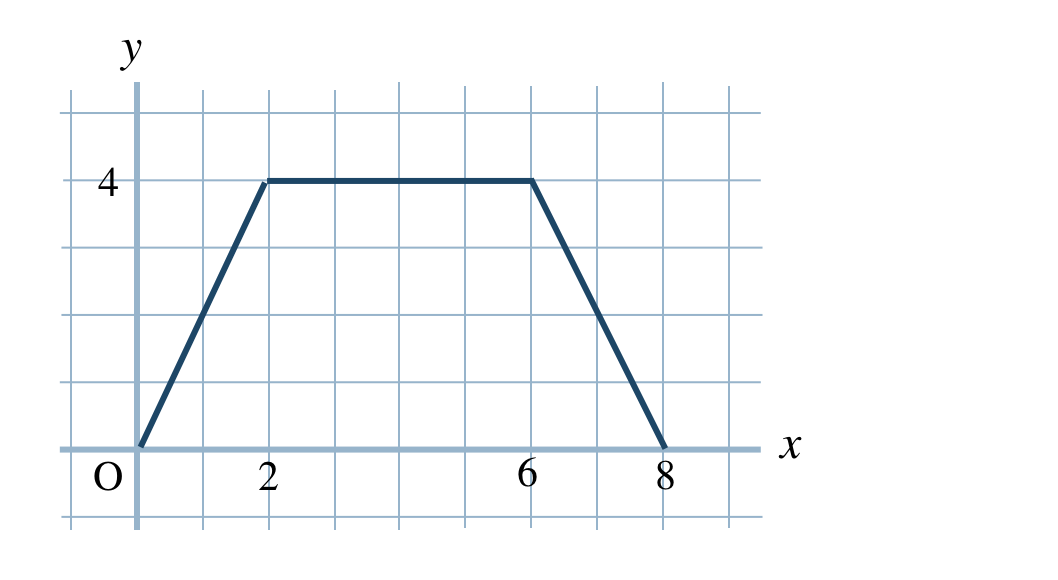
\(\begin{split}~~~y=-2x+16\end{split}\)
■ 同じタイプの例題解説
» １次関数と動く点
» １次関数と動く点
次のページ「４章 図形の性質と合同」
