学校図書：中学校数学３

p.141 問1\({\small (1)}~\)

\({\small (2)}~\)

p.141 問2

p.141 問3　画びょう

p.142 問1　\({\rm A’C’:AC}=3:1\)
　\({\rm B’D’:BD}=3:1\)

p.142 問2　\({\rm A’B’:AB}=2:1~,~{\rm B’C’:BC}=2:1\)
　\({\rm A’C’:AC}=2:1\)
　\(\angle{\rm A’}=\angle{\rm A}~,~\angle{\rm B’}=\angle{\rm B}~,~\angle{\rm C’}=\angle{\rm C}\)

p.143 問3　いえる

p.143 問4\({\small (1)}~\)いえる　　\({\small (2)}~\)いえない
\({\small (3)}~\)いえる

p.144 問5　\(2:3\)

p.144 問6　合同

p.145 問7　\(\begin{split}\frac{\,21\,}{\,2\,}=10.5~{\rm cm}\end{split}\)

p.145 問8　\(\begin{split}{\rm DC}=6~{\rm cm}~,~ {\rm EH}=\frac{\,15\,}{\,2\,}=7.5~{\rm cm}\end{split}\)

p.146 問1 問2

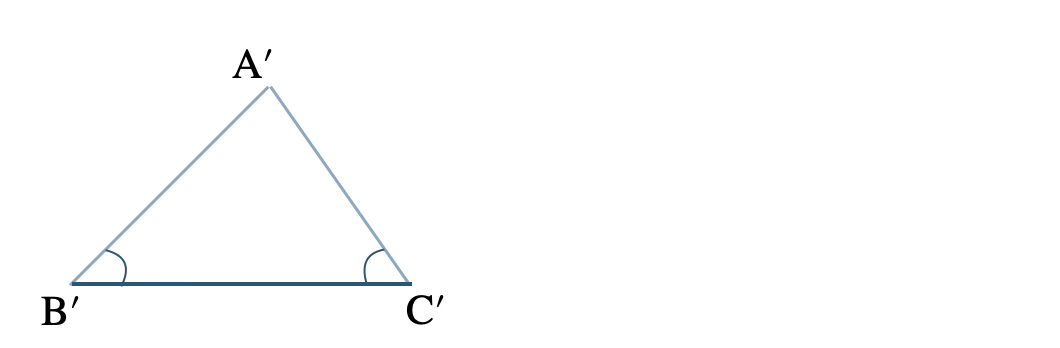
① \({\rm B’C’}=2a\) の線分を引く。
② \(\angle{\rm B’}=\angle{\rm B}\) となる直線を引く。
③ この直線上に \({\rm B’A’}=2c\) となる点 \({\rm A’}\) をとる。

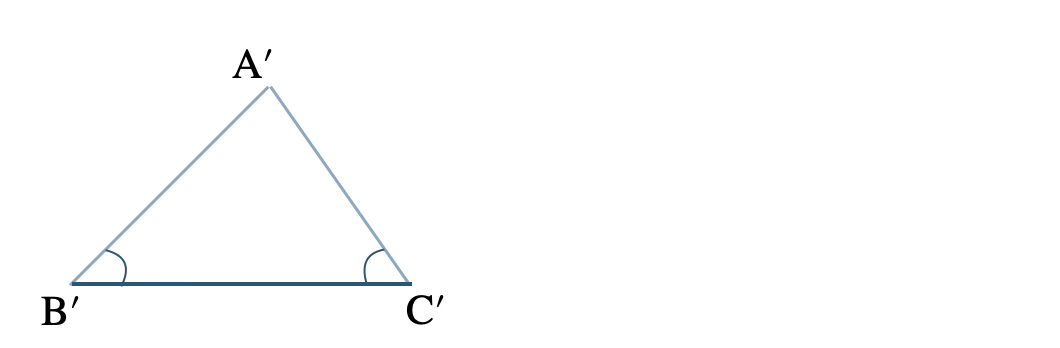
① \({\rm B’C’}=2a\) の線分を引く。
② \(\angle{\rm B’}=\angle{\rm B}\) となる直線を引く。
③ \(\angle{\rm C’}=\angle{\rm C}\) となる直線を引き、②の直線との交点が点 \({\rm A’}\) となる。

p.147 問3アとカ
２組の辺の比とその間の角がそれぞれ等しい

---

イとキ
２組の角がそれぞれ等しい

---

オとエ
３組の辺の比がすべて等しい

p.148 問4\({\small (1)}~\)\(\triangle {\rm AOC}\,\,\unicode{x223D}\,\,\triangle {\rm CBD}\)
２組の辺の比とその間の角がそれぞれ等しい

---

\({\small (2)}~\)\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm ADE}\)
２組の角がそれぞれ等しい

---

\({\small (3)}~\)\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm CBD}\)
２組の辺の比とその間の角がそれぞれ等しい

p.148 問5　\(4:3~,~4:3\)
　\(\angle{\rm AOC}=\angle{\rm BOD}\)
　２組の辺の比とその間の角がそれぞれ等しい

p.149 問6[証明] \(\triangle {\rm ABC}\) と \(\triangle {\rm DAC}\) において、
仮定より、
　\(\angle{\rm BAC}=\angle{\rm ADC}=90^\circ~~\cdots{\large ①}\)
共通の角より、
　\(\angle{\rm ACB}=\angle{\rm DCA}~~\cdots{\large ②}\)
①、②より、
２組の角がそれぞれ等しいから、
　\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm DAC}\)
[終]

p.149 問7　\(\begin{split}{\rm AC}=\frac{\,15\,}{\,2\,}=7.5~{\rm cm}\end{split}\)

---

　\(\begin{split}{\rm CD}=\frac{\,9\,}{\,2\,}=4.5~{\rm cm}\end{split}\)

p.149 問8\({\small (1)}~\)[証明] \(\triangle {\rm ABC}\) と \(\triangle {\rm DAC}\) において、
仮定より、
　\({\rm AC:DC}=2:1~~\cdots{\large ①}\)
　\({\rm BC:AC}=2:1~~\cdots{\large ②}\)
共通の角より、
　\(\angle{\rm ACB}=\angle{\rm DCA}~~\cdots{\large ③}\)
①、②、③より、
２組の辺の比とその間の角が、それぞれ等しいので、
　\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm DAC}\)
[終]

---

\({\small (2)}~\)\({\rm AD}=5~{\rm cm}\)

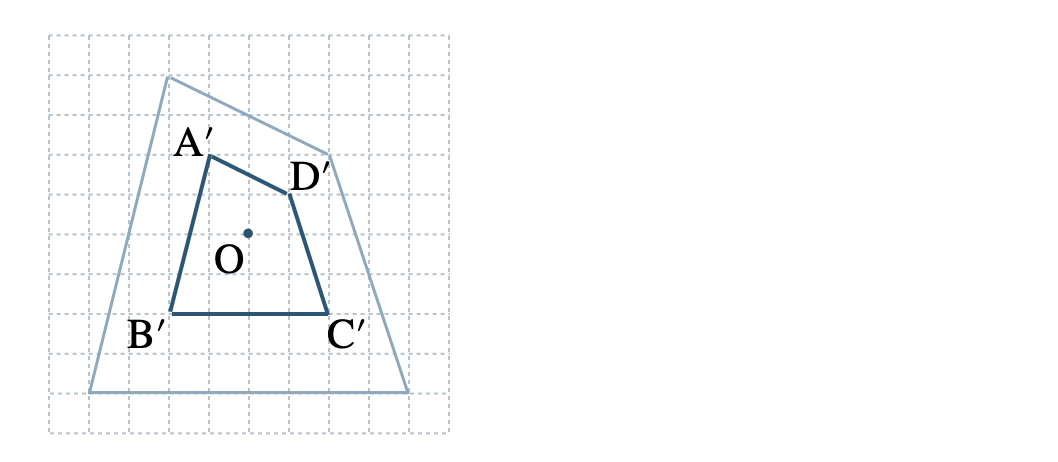
p.150 問9\({\small (1)}~\)[証明] \(\triangle {\rm OA’B’}\) と \(\triangle {\rm OAB}\) において、
仮定より、
　\({\rm OA’:OA}=3:1~~\cdots{\large ①}\)
　\({\rm OB’:OB}=3:1~~\cdots{\large ②}\)
共通の角より、
　\(\angle{\rm A’OB’}=\angle{\rm AOB}~~\cdots{\large ③}\)
①、②、③より、
２組の辺の比とその間の角が、それぞれ等しいので、
　\(\triangle {\rm OA’B’}\,\,\unicode{x223D}\,\,\triangle {\rm OAB}\)
[終]

---

\({\small (2)}~\)相似な図形の対応する辺の比は等しいから
　\({\rm A’B’:AB}=3:1\)

---

\({\small (3)}~\)平行

---

\({\small (4)}~\)[証明] \(\triangle {\rm ABC}\) と \(\triangle {\rm A’B’C’}\) において、
\({\small (2)}\) より、
　\({\rm AB:A’B’}=1:3~~\cdots{\large ①}\)
同様に考えて、
　\({\rm BC:B’C’}=1:3~~\cdots{\large ②}\)
　\({\rm AC:A’C’}=1:3~~\cdots{\large ③}\)
①、②、③より、
３組の辺の比が、それぞれ等しいから、
　\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm A’B’C’}\)
[終]

p.151 問1　\(140~{\rm m}\)

p.151 問2　\(18.3~{\rm m}\)

p.153 問3\({\rm A’B’}\) の長さを約 \(3.6~{\rm cm}\) としているから

p.153 問4\({\small (1)}~25.55≦ a < 25.65\)
誤差の絶対値は \(0.05~{\rm m}\) 以下

---

\({\small (2)}~1.825≦ a < 1.835\)
誤差の絶対値は \(0.005~{\rm m}\) 以下

p.154 問5　\(1~,~2~,~6\)

p.154 問6\({\small (1)}~2.5{\, \small \times \,}10^2~{\rm g}\)　　\({\small (2)}~6.0{\, \small \times \,}10^3~{\rm km}\)

---

\(\begin{split}{\small (3)}~8.0{\, \small \times \,}\frac{\,1\,}{\,10\,}~{\rm m}\end{split}\)

p.154 問7　\(0.0005{\, \small \times \,}10^3=0.5~{\rm m}\) 以下

p.155 確かめよう 1\(\begin{split}{\small (1)}~\end{split}\)点 \({\rm C}\)　　\(\begin{split}{\small (2)}~\frac{\,3\,}{\,2\,}\end{split}\) 倍

p.155 確かめよう 2\({\small (1)}~3:2\)　　\({\small (2)}~12~{\rm cm}\)　　\({\small (3)}~100^\circ\)

p.155 確かめよう 3\({\small (1)}~\)\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm AED}\)
２組の角がそれぞれ等しい

---

\({\small (2)}~\)\(\triangle {\rm ADO}\,\,\unicode{x223D}\,\,\triangle {\rm CBO}\)
２組の辺の比とその間の角がそれぞれ等しい

p.155 確かめよう 4[証明] \(\triangle {\rm ADC}\) と \(\triangle {\rm BEC}\) において、
仮定より、
　\(\angle{\rm ADC}=\angle{\rm EC}=90^\circ~~\cdots{\large ①}\)
共通の角より、
　\(\angle{\rm ACD}=\angle{\rm BCE}~~\cdots{\large ②}\)
①、②より、
２組の角がそれぞれ等しいから、
　\(\triangle {\rm ADC}\,\,\unicode{x223D}\,\,\triangle {\rm BEC}\)
[終]

p.155 確かめよう 5\(\begin{split}{\small (1)}~3.19{\, \small \times \,}10^3~{\rm m}\end{split}\)
誤差の絶対値は \(\begin{split}5~{\rm m}\end{split}\) 以下

---

\(\begin{split}{\small (2)}~5.26{\, \small \times \,}\frac{\,1\,}{\,10\,}~{\rm kg}\end{split}\)

---

誤差の絶対値は \(\begin{split}0.0005=5.00{\, \small \times \,}\frac{\,1\,}{\,10^4\,}~{\rm m}\end{split}\) 以下

p.157 問1\({\small (1)}~\)[証明] \(\triangle {\rm APQ}\) と \(\triangle {\rm ABC}\) において、
\({\rm PQ \,//\, BC}\) より、平行線の同位角は等しいから、
\(\begin{split}~~~\angle{\rm APQ}=\angle{\rm ABC}~~~\cdots{\large ①}\end{split}\)
また、\(\angle {\rm A}\) は共通 \(~~~\cdots{\large ②}\)
①、②より、２組の角がそれぞれ等しいから、
\(\begin{split}~~~\triangle {\rm APQ}∽\triangle {\rm ABC}\end{split}\)
[終]

---

\({\small (2)}~{\rm AQ:AC~,~PQ:BC}\)

p.157 問2[証明] 点Ｐを通り、辺ＡＣに平行な直線をひき、辺ＢＣとの交点をＲとする
\(\triangle {\rm APQ}\) と \(\triangle {\rm PBR}\) において、
\({\rm PQ \,//\, BC}\) より、平行線の同位角は等しいから、
\(\begin{split}~~~\angle{\rm APQ}=\angle{\rm PBR}~~~\cdots{\large ①}\end{split}\)
また、\({\rm AQ \,//\, PR}\) より、平行線の同位角は等しいから、
\(\begin{split}~~~\angle{\rm PAQ}=\angle{\rm BPR}~~~\cdots{\large ②}\end{split}\)
①、②より、２組の角がそれぞれ等しいから、
\(\begin{split}~~~\triangle {\rm APQ}∽\triangle {\rm PBR}\end{split}\)
相似な図形の対応する辺の比は等しいから、
\(\begin{split}~~~{\rm AP:PB=AQ:PR}~~~\cdots{\large ③}\end{split}\)
また、四角形ＤＦＣＥは、
\(\begin{split}~~~{\rm PQ\,//\,RC~,~PR\,//\,QC}\end{split}\)
これより、平行四辺形である
平行四辺形の２組の対辺はそれぞれ等しいから、
\(\begin{split}~~~{\rm PR=QC}~~~\cdots{\large ④}\end{split}\)
③と④より、
\(\begin{split}~~~{\rm AP:PB=AQ:QC}\end{split}\)
[終]

p.158 問3等間隔に引かれた平行線にそって切ると、ロールケーキの幅が等間隔になる

p.158 問4[証明] \(\triangle {\rm ABC}\) と \(\triangle {\rm APQ}\) において、
錯角が等しいから、
　\(\angle{\rm ABC}=\angle{\rm APQ}~~\cdots{\large ①}\)
対頂角が等しいから、
　\(\angle{\rm BAC}=\angle{\rm PAQ}~~\cdots{\large ②}\)
①、②より、
２組の角がそれぞれ等しいから、
　\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm APQ}\)
したがって、
　\({\rm AP:AB=AQ:AC=PQ:BC}\)
[終]

p.159 問5\({\rm AP:PB}\) と \({\rm PQ:BC}\) は等しくない

---

\(\begin{eqnarray}~~~{\rm AP:AB}&=&{\rm PQ:BC}
\\[2pt]~~~6:9&=&7:y
\\[2pt]~~~6y&=&63
\\[3pt]~~~y&=&\frac{\,21\,}{\,2\,}
\end{eqnarray}\)

p.159 問6\(\begin{split}{\small (1)}~x=\frac{\,9\,}{\,2\,}~{\rm cm}\end{split}\)　　\(\begin{split}{\small (2)}~x=8~{\rm cm}\end{split}\)

---

\(\begin{split}{\small (3)}~x=12~{\rm cm}~,~y=12~{\rm cm}\end{split}\)
\(\begin{split}{\small (4)}~x=6~{\rm cm}~,~y=5~{\rm cm}\end{split}\)

p.161 問7\(\begin{split}{\small (1)}~x=7~{\rm cm}\end{split}\)
\(\begin{split}{\small (2)}~x=10~{\rm cm}~,~y=12~{\rm cm}\end{split}\)

---

\(\begin{split}{\small (3)}~x=\frac{\,25\,}{\,6\,}~{\rm cm}\end{split}\)

p.161 問8\({\rm PS\,//\,QT}\) と \({\rm AP:PQ}=1:1\) より、
　\({\rm AS:ST}=1:1\)
\({\rm QT\,//\,RB}\) と \({\rm PQ:QR}=1:1\) より、
　\({\rm ST:TB}=1:1\)
よって、
　\({\rm AS:ST:TB}=1:1:1\)
これより、\({\rm AB}\) が３等分される

p.161 問9

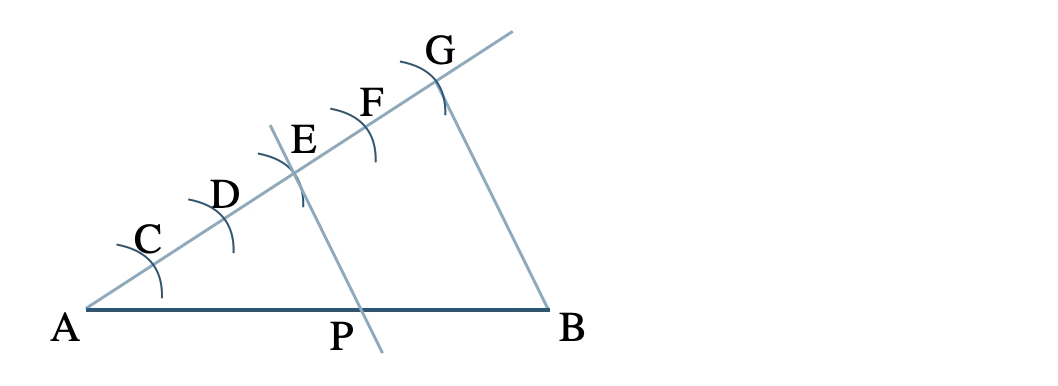
① 適当な半直線ＡＸを引く
② 半直線ＡＸ上に、点Ａから等しい長さで、順に点Ｃ、Ｄ、Ｅ、Ｆ、Ｇをとり、点Ｇと点Ｂを結ぶ
③ 点ＥからＧＢに平行な直線を引き、ＡＢとの交点がＰとなる

p.162 問1\({\small (1)}~\)\({\rm AP:AB}=3:5\)
　　\({\rm AQ:AC}=3:5\)

---

\({\small (2)}~\)[証明] \(\triangle {\rm APQ}\) と \(\triangle {\rm ABC}\) において、
\({\small (1)}\) より、
　\({\rm AP:AB}=3:5~~\cdots{\large ①}\)
　\({\rm AQ:AC}=3:5~~\cdots{\large ②}\)
共通の角より、
　\(\angle{\rm PAQ}=\angle{\rm BAC}~~\cdots{\large ③}\)
①、②、③より、
２組の辺の比とその間の角が、それぞれ等しいので、
　\(\triangle {\rm APQ}\,\,\unicode{x223D}\,\,\triangle {\rm BAC}\)
したがって、
　\(\angle{\rm APQ}=\angle{\rm ABC}\)
錯角が等しいので、
　\({\rm PQ\,//\,BC}\)
[終]

p.163 問2　\({\rm PQ\,//\,AC}\)

p.163 問3[証明] \(\triangle {\rm APQ}\) と \(\triangle {\rm ABC}\) において、
仮定より、
　\({\rm AP:AB}=1:2~~\cdots{\large ①}\)
　\({\rm AQ:AC}=1:2~~\cdots{\large ②}\)
対頂角が等しいので、
　\(\angle{\rm PAQ}=\angle{\rm BAC}~~\cdots{\large ③}\)
①、②、③より、
２組の辺の比とその間の角が、それぞれ等しいので、
　\(\triangle {\rm APQ}\,\,\unicode{x223D}\,\,\triangle {\rm BAC}\)
したがって、
　\(\angle{\rm APQ}=\angle{\rm ABC}\)
錯角が等しいので、
　\({\rm PQ\,//\,BC}\)
[終]

p.164 問4　\(\triangle {\rm ADF}~,~\triangle {\rm DBE}~,~\triangle {\rm FEC}\)

p.164 問5　\(8~{\rm cm}\)

p.167 確かめよう 1\(\begin{split}{\small (1)}~x=2~{\rm cm}~,~y=\frac{\,15\,}{\,2\,}=7.5~{\rm cm}\end{split}\)

---

\(\begin{split}{\small (2)}~x=\frac{\,48\,}{\,5\,}=9.6~{\rm cm}~,~y=15~{\rm cm}\end{split}\)

p.167 確かめよう 2\(\begin{split}{\small (1)}~x=6~{\rm cm}\end{split}\)

---

\(\begin{split}{\small (2)}~x=\frac{\,7\,}{\,2\,}=3.5~{\rm cm}\end{split}\)

p.167 確かめよう 3　\({\rm AD\,//\,EF}\)

---

　\({\rm OA:AE}=3:6=1:2\)
　\({\rm OB:BE}=4:8=1:2\)

p.167 確かめよう 4\(\begin{split}{\small (1)}~\end{split}\)二等辺三角形

---

\(\begin{split}{\small (2)}~\end{split}\)[証明]\(\triangle {\rm DAB}\) において、
仮定より、
　\(\begin{split}{\rm GE}=\frac{\,1\,}{\,2\,}{\rm AB}~~\cdots{\large ①}\end{split}\)

---

\(\triangle {\rm BDC}\) において、
仮定より、
　\(\begin{split}{\rm EF}=\frac{\,1\,}{\,2\,}{\rm DC}~~\cdots{\large ①}\end{split}\)

---

①と②と \({\rm AB=DC}\) より、
　\({\rm GE=EF}\)
よって、
２辺が等しいので、\(\triangle {\rm EFG}\) は二等辺三角形

p.169 問1　\(25\) 倍

p.170 問2　相似比 \(3:5\)
　円周の長さの比 \(3:5\)
　面積比 \(9:25\)

p.170 問3\({\small (1)}~4:9\)　　\({\small (2)}~25~{\rm cm}^2\)

p.170 問4　\(\triangle {\rm OAD}=16~{\rm cm}^2\)、\(\triangle {\rm OAB}=24~{\rm cm}^2\)
　台形 \({\rm ABCD}=100~{\rm cm}^2\)

p.171 問1\({\small (1)}~\)いえる　　\({\small (2)}~\)いえない
\({\small (3)}~\)いえない　　\({\small (4)}~\)いえる

p.172 問2　相似比 \(5:2\)、表面積比 \(25:4\)
　体積比 \(125:8\)

p.173 問3\({\small (1)}~320~{\rm cm}^2\)　　\({\small (2)}~108~{\rm cm}^3\)

p.173 問4　\(1:26\)

p.174 確かめよう 1\({\small (1)}~4:9\)　　\({\small (2)}~72~{\rm cm}^2\)

p.174 確かめよう 2　相似比 \(3:4\)、表面積比 \(9:16\)
　体積比 \(27:64\)