このページは「中学数学２ 三角形と四角形」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう！
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
【問題一覧】中学数学２ 三角形と四角形
二等辺三角形の性質
次の問いに答えよ。
\({\small (1)}~\)次の \({\rm AB=AC}\) 二等辺三角形 \(\triangle {\rm ABC}\) について、
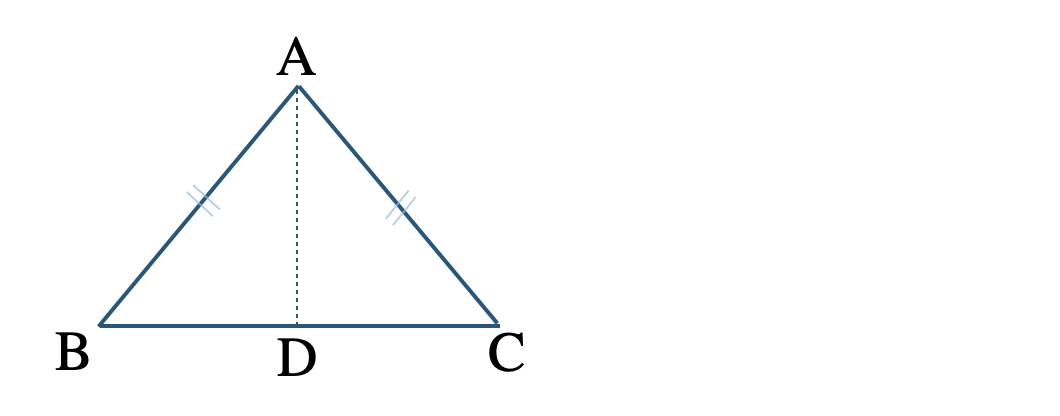
\(~~{\large ①}~\)二等辺三角形の定義を答えよ。
\(~~{\large ②}~\)\(\angle {\rm A}\) を何というか答えよ。
\(~~{\large ③}~\)辺 \({\rm BC}\) を何というか答えよ。
\(~~{\large ④}~\)\(\angle {\rm B}~,~\angle {\rm C}\) を何というか答えよ。また、\(\angle {\rm B}\) と \(\angle {\rm C}\) の関係を答えよ。
\(~~{\large ⑤}~\)\(\angle {\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) とするとき、二等分線 \({\rm AD}\) と辺 \({\rm BC}\) の関係、線分 \({\rm BD}\) と \({\rm CD}\) の関係をそれぞれ答えよ。
\({\small (2)}~\)次の \(\triangle {\rm ABC}\) が \({\rm AB=AC}\) の二等辺三角形であるとき、\(\angle x~,~\angle y\) の大きさを求めよ。
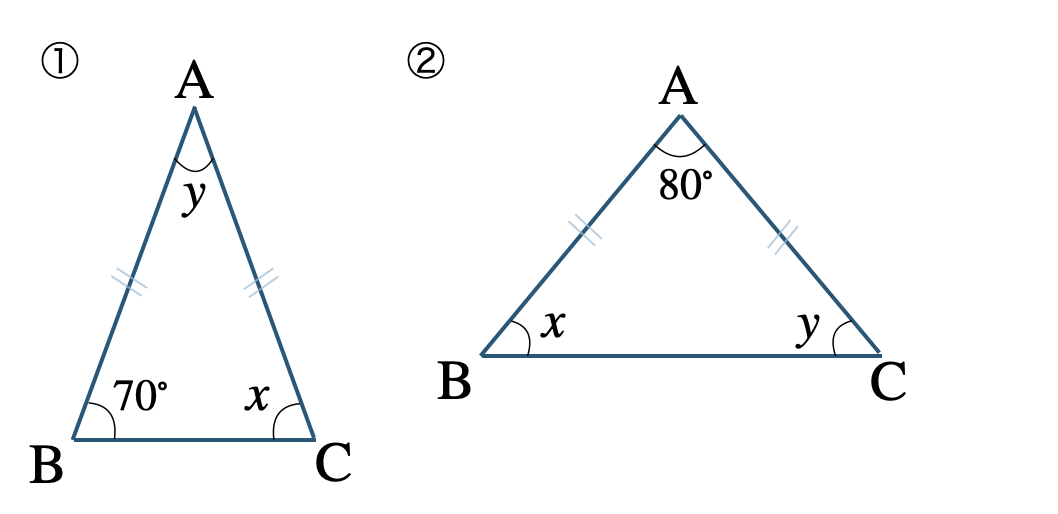
[ 解答を見る ]
【解答】
\({\small (1)}~\)
\(~~{\large ①}~\)２つの辺が等しい三角形を二等辺三角形という
\(~~{\large ②}~\)\(\angle {\rm A}\) は頂角
\(~~{\large ③}~\)辺 \({\rm BC}\) は底辺
\(~~{\large ④}~\)\(\angle {\rm B}~,~\angle {\rm C}\) は底角、\(\angle {\rm B}=\angle {\rm C}\)
\(~~{\large ⑤}~\)\({\rm AD\perp BC~,~BD=CD}\)
\({\small (2)}~\)
\(~~{\large ①}~\angle x=70^\circ~,~\angle y=40^\circ\)
\(~~{\large ②}~\angle x=50^\circ~,~\angle y=50^\circ\)
詳しい解説ページはこちらから↓
二等辺三角形の証明
次の証明をせよ。
\({\small (1)}~\)\(\triangle {\rm ABC}\) において、
\({\rm AB=AC}\) ならば \(\angle{\rm B}=\angle{\rm C}\)
であることを、\(\angle {\rm A}\) の二等分線をひくことで証明せよ。
\({\small (2)}~\)\({\rm AB=AC}\) の二等辺三角形 \(\triangle {\rm ABC}\) において、\(\angle {\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) とすると、\({\rm AD\perp BC}\) であることを証明せよ。
\({\small (3)}~\)次の図において、\({\rm AB=AC~,~BD=CD}\) であるとき、
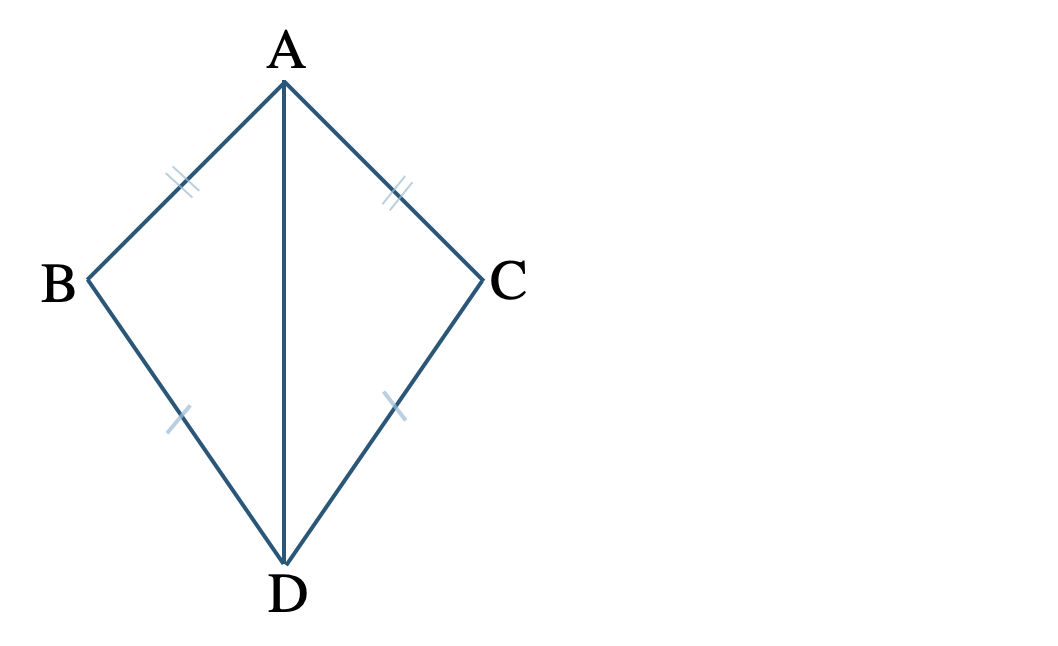
\(\angle{\rm BAD}=\angle{\rm CAD}\) であることを証明せよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)[証明] \(\angle{\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) とする
\(\triangle {\rm ABD}\) と \(\triangle {\rm ACD}\) について、
仮定より、$$~~~{\rm AB=AC}~~~\cdots{\large ①}$$線分 \({\rm AD}\) は \(\angle{\rm A}\) の二等分するので、$$~~~\angle{\rm BAD}=\angle{\rm CAD}~~~\cdots{\large ②}$$また、共通の辺より、$$~~~{\rm AD=AD}~~~\cdots{\large ③}$$①、②、③より、２組の辺とその間の角がそれぞれ等しいので、$$~~~\triangle {\rm ABD}\equiv\triangle {\rm ACD}$$合同な図形では、対応する角が等しいから、$$~~~\angle{\rm ABD}=\angle{\rm ACD}$$よって、$$~~~\angle{\rm B}=\angle{\rm C}$$したがって、
\({\rm AB=AC}\) ならば \(\angle{\rm B}=\angle{\rm C}\)
となる [終]
\({\small (2)}~\)[証明] (1)より、\(\triangle {\rm ABD}\equiv\triangle {\rm ACD}\) であり、合同な図形では、対応する角が等しいから、$$~~~\angle{\rm ADB}=\angle{\rm ADC}~~~\cdots{\large ①}$$また、$$~~~\angle{\rm ADB}+\angle{\rm ADC}=180^\circ~~~\cdots{\large ②}$$①を代入すると、$$\begin{eqnarray}~~~\angle{\rm ADB}+\angle{\rm ADC}&=&180^\circ\\[2pt]~~~2\angle{\rm ADB}&=&180^\circ\\[2pt]~~~\angle{\rm ADB}&=&90^\circ\end{eqnarray}$$したがって、\({\rm AD\perp BC}\) [終]
\({\small (3)}~\)[証明] \(\triangle {\rm ABD}\) と \(\triangle {\rm ACD}\) について、
仮定より、$$~~~{\rm AB=AC}~~~\cdots{\large ①}$$$$~~~{\rm BD=CD}~~~\cdots{\large ②}$$また、共通の辺より、$$~~~{\rm AD=AD}~~~\cdots{\large ③}$$①、②、③より、３組の辺がそれぞれ等しいので、$$~~~\triangle {\rm ABD}\equiv\triangle {\rm ACD}$$合同な図形では、対応する角が等しいから、$$~~~\angle{\rm BAD}=\angle{\rm CAD}$$[終]
詳しい解説ページはこちらから↓
二等辺三角形になるための条件
次の証明をせよ。
\({\small (1)}~\)\(\triangle {\rm ABC}\) において、
\(\angle{\rm B}=\angle{\rm C}\) ならば \({\rm AB=AC}\)
であることを、\(\angle {\rm A}\) の二等分線をひくことで証明せよ。
\({\small (2)}~\)\({\rm AB=AC}\) の二等辺三角形 \(\triangle {\rm ABC}\) において、底角 \(\angle{\rm B}~,~\angle{\rm C}\) のそれぞれの二等分線をひいて、その交点を \({\rm P}\) とする
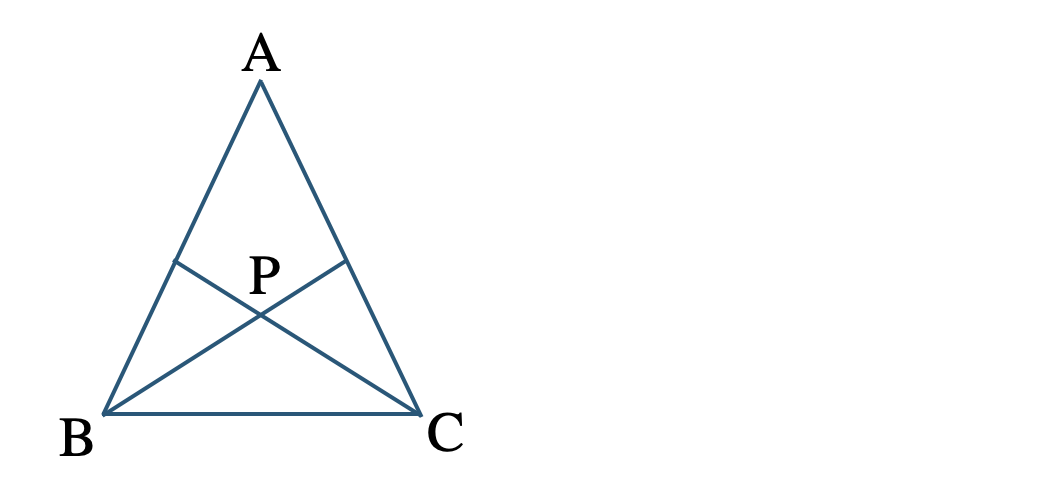
このとき、\(\triangle {\rm PBC}\) が二等辺三角形であることを証明せよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)[証明] \(\angle{\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) とする
\(\triangle {\rm ABD}\) と \(\triangle {\rm ACD}\) について、
仮定より、$$~~~\angle{\rm ABD}=\angle{\rm ACD}~~~\cdots{\large ①}$$線分 \({\rm AD}\) は \(\angle{\rm A}\) の二等分するので、$$~~~\angle{\rm BAD}=\angle{\rm CAD}~~~\cdots{\large ②}$$①、②と三角形の内角の和が \(180^\circ\) より、残りの角も等しいので、$$~~~\angle{\rm ADB}=\angle{\rm ADC}~~~\cdots{\large ③}$$また、共通の辺より、$$~~~{\rm AD=AD}~~~\cdots{\large ④}$$②、③、④より、１組の辺とその両端の角がそれぞれ等しいので、$$~~~\triangle {\rm ABD}\equiv\triangle {\rm ACD}$$合同な図形では、対応する角が等しいから、$$~~~{\rm AB=AC}$$[終]
\({\small (2)}~\)[証明] \(\triangle {\rm ABC}\) は \({\rm AB=AC}\) の二等辺三角形より、底角が等しいので、$$~~~\angle{\rm ABC}=\angle{\rm ACB}~~~\cdots{\large ①}$$また、\({\rm BP}\) と \({\rm CP}\) はそれぞれ \(\angle{\rm B}=\angle{\rm C}\) の二等分線であるので、$$~~~\angle{\rm PBC}=\frac{\,1\,}{\,2\,}\angle{\rm ABC}~~~\cdots{\large ②}$$$$~~~\angle{\rm PCB}=\frac{\,1\,}{\,2\,}\angle{\rm ACB}~~~\cdots{\large ③}$$①、②、③より、$$~~~\angle{\rm PBC}=\angle{\rm PCB}$$これより、\(\triangle {\rm PBC}\) の２つの角が等しいので、
\(\triangle {\rm PBC}\) は二等辺三角形である [終]
詳しい解説ページはこちらから↓
ことがらの逆と反例
次のことがらの逆を答えよ。また、それが正しいかどうかを調べて正しくない場合は反例も答えよ。
\({\small (1)}~\)\(\triangle {\rm ABC}\) で、
\({\rm AB=AC}\) ならば \(\angle{\rm B}=\angle{\rm C}\)
\({\small (2)}~\)\(a\) も \(b\) も奇数 ならば \(a+b\) は偶数。
\({\small (3)}~\)\(\triangle {\rm ABC}\) で、
\(\angle{\rm A}\) が直角 ならば \(\angle{\rm B}+\angle{\rm C}=90^\circ\)
\({\small (4)}~\)２直線が平行 ならば 錯角が等しい。
\({\small (5)}~\)２つの三角形が合同 ならば その２つの三角形の面積が等しい。
\({\small (6)}~\)\(x\) が \(6\) の倍数 ならば \(x\) は \(2\) の倍数。
\({\small (7)}~\)\(a\) が奇数で \(b\) が偶数 ならば \(ab\) は偶数。
\({\small (8)}~\)\(\triangle {\rm ABC}\) と \(\triangle {\rm A’B’C’}\) において、
\(\triangle {\rm ABC}\equiv\triangle {\rm A’B’C’}\) ならば \({\rm AB=A’B’}\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)正しい
\({\small (2)}~\)正しくない、反例は \(a=2~,~b=4\)
\({\small (3)}~\)正しい
\({\small (4)}~\)正しい
\({\small (5)}~\)正しくない、反例は、
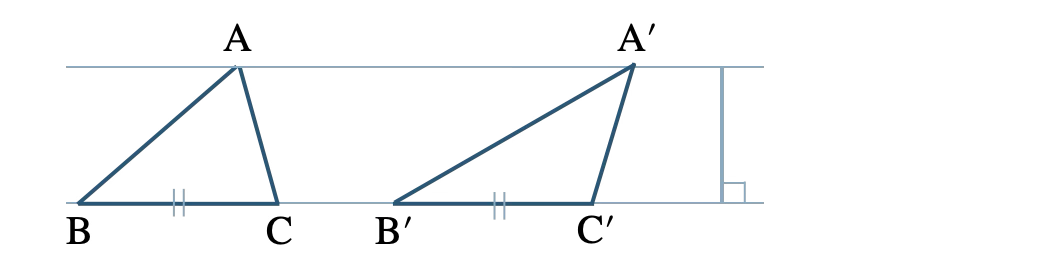
\({\small (6)}~\)正しくない、反例は \(x=4\)
\({\small (7)}~\)正しくない、反例は \(a=2~,~b=3\)
\({\small (8)}~\)正しくない、反例は、
詳しい解説ページはこちらから↓
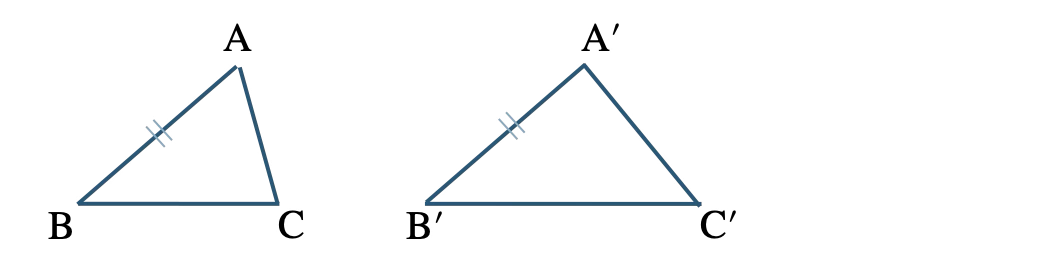
正三角形の性質
次の証明をせよ。
\({\small (1)}~\)\(\triangle {\rm ABC}\) において、
\({\rm AB=BC=CA}\)
ならば \(\angle{\rm A}=\angle{\rm B}=\angle{\rm C}\)
であることを証明せよ。
\({\small (2)}~\)３つの角がすべて等しい \(\triangle {\rm ABC}\) は正三角形であることを証明せよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)[証明] \(\triangle {\rm ABC}\) において、
\({\rm AB=AC}\) より、\(\angle{\rm A}\) を頂角とする二等辺三角形となる
よって、底角が等しいので、$$~~~\angle{\rm B}=\angle{\rm C}~~~\cdots{\large ①}$$また、\({\rm BA=BC}\) より、\(\angle{\rm B}\) を頂角とする二等辺三角形となる
よって、底角が等しいので、$$~~~\angle{\rm A}=\angle{\rm C}~~~\cdots{\large ②}$$したがって、①と②より、$$~~~\angle{\rm A}=\angle{\rm B}=\angle{\rm C}$$[終]
\({\small (2)}~\)[証明] \(\triangle {\rm ABC}\) において、
\(\angle{\rm B}=\angle{\rm C}\) より、底角が等しいので、\(\angle{\rm A}\) を頂角とする二等辺三角形となる
よって、二等辺三角形の定義より、$$~~~{\rm AB=AC}~~~\cdots{\large ①}$$また、\(\angle{\rm A}=\angle{\rm C}\) より、底角が等しいので、\(\angle{\rm B}\) を頂角とする二等辺三角形となる
よって、二等辺三角形の定義より、$$~~~{\rm BA=BC}~~~\cdots{\large ②}$$①、②より、$$~~~{\rm AB=BC=CA}$$したがって、３つの辺が等しいので、
\(\triangle {\rm ABC}\) は正三角形
である [終]
詳しい解説ページはこちらから↓
直角三角形の合同条件
次の問いに答えよ。
\({\small (1)}~\)次の図において、合同な図形を見つけ記号 \(\equiv\) で表し、合同条件を答えよ。
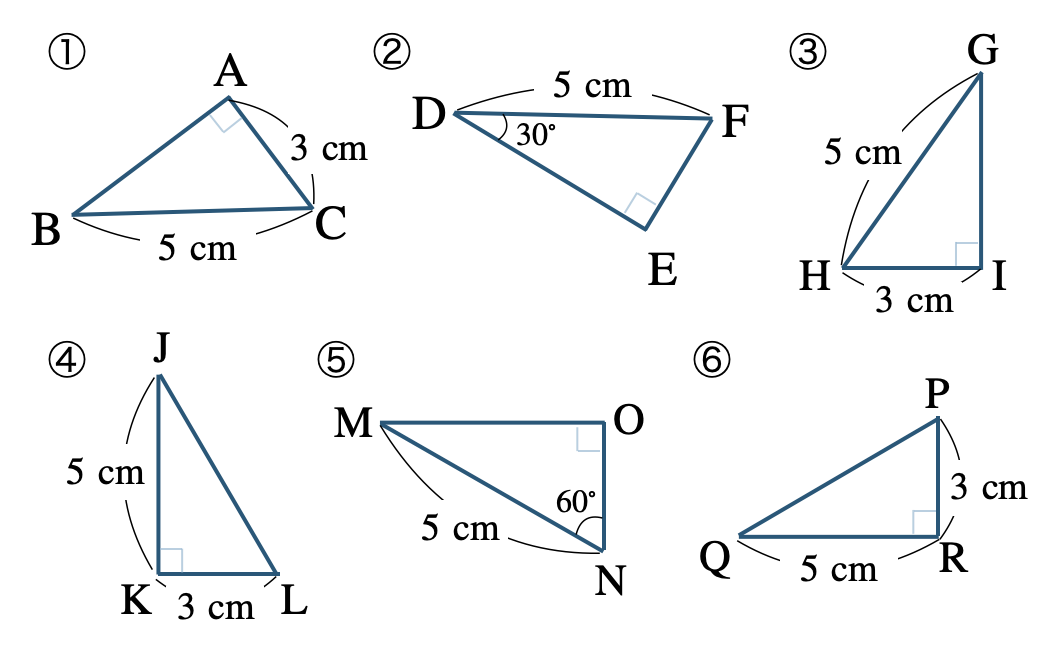
\({\small (2)}~\)次の図において、合同な図形を見つけ記号 \(\equiv\) で表し、合同条件を答えよ。
\(~~{\large ①}~\)\(\triangle {\rm ABC}\) は \({\rm AB=AC}\) の二等辺三角形で、点 \({\rm A}\) から辺 \({\rm BC}\) におろした垂線との交点を \({\rm D}\) とする。
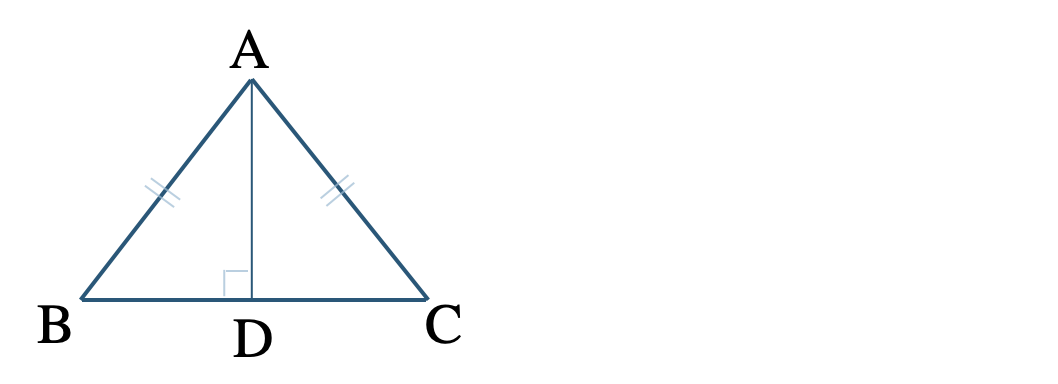
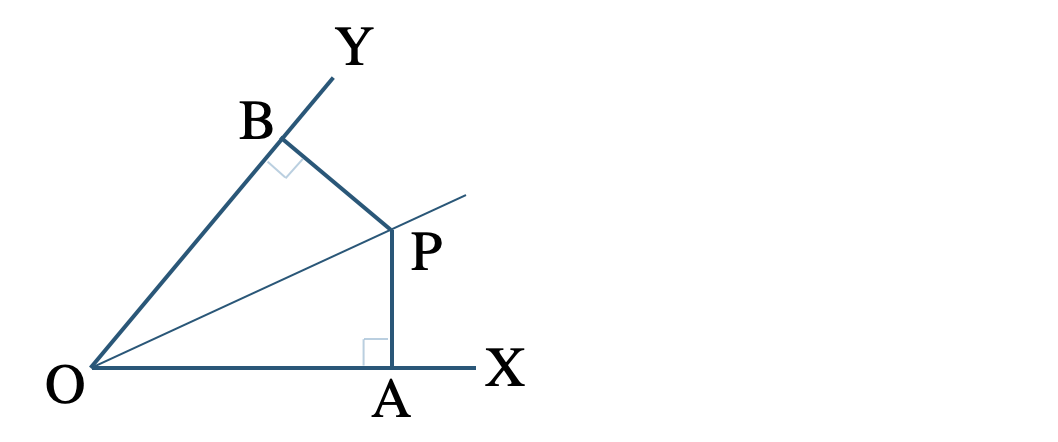
\(~~{\large ②}~\)直線 \({\rm OP}\) は \(\angle{\rm XOY}\) の二等分線で、点 \({\rm P}\) からそれぞれ直線 \({\rm OX~,~OY}\) におろした垂線との交点を \({\rm A~,~B}\) とする。
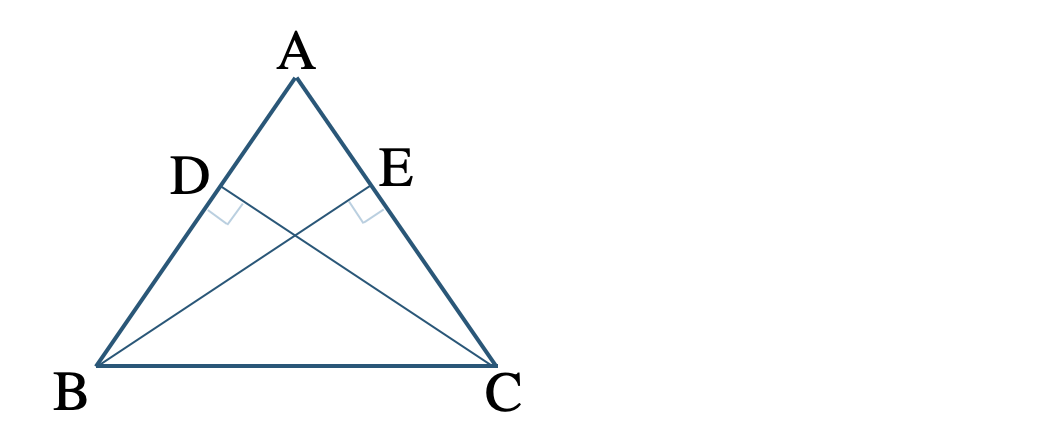
\(~~{\large ③}~\)\(\triangle {\rm ABC}\) は \({\rm AB=AC}\) の二等辺三角形で、点 \({\rm B~,~C}\) からそれぞれ辺 \({\rm AC~,~AB}\) におろした垂線との交点を \({\rm E~,~D}\) とする。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
①と③ \(\triangle {\rm ABC}\equiv\triangle {\rm IGH}\)
直角三角形の斜辺と他の１辺がそれぞれ等しい
②と⑤ \(\triangle {\rm DEF}\equiv\triangle {\rm MON}\)
直角三角形の斜辺と１つの鋭角がそれぞれ等しい
④と⑥ \(\triangle {\rm JKL}\equiv\triangle {\rm QRP}\)
２組の辺とその間の角がそれぞれ等しい
\({\small (2)}~\)
\(~~{\large ①}~\)\(\triangle {\rm ABD}\equiv\triangle {\rm ACD}\)
直角三角形の斜辺と他の１辺がそれぞれ等しい
\(~~{\large ②}~\)\(\triangle {\rm POA}\equiv\triangle {\rm POB}\)
直角三角形の斜辺と１つの鋭角がそれぞれ等しい
\(~~{\large ③}~\)\(\triangle {\rm DBC}\equiv\triangle {\rm ECB}\)
直角三角形の斜辺と１つの鋭角がそれぞれ等しい
詳しい解説ページはこちらから↓
直角三角形の証明
次の証明をせよ。
\({\small (1)}~\)\(\triangle {\rm ABC}\) は \({\rm AB=AC}\) の二等辺三角形で、点 \({\rm A}\) から辺 \({\rm BC}\) に垂線をひき、その交点を \({\rm D}\) とするとき、\({\rm BD=CD}\) となることを証明せよ。
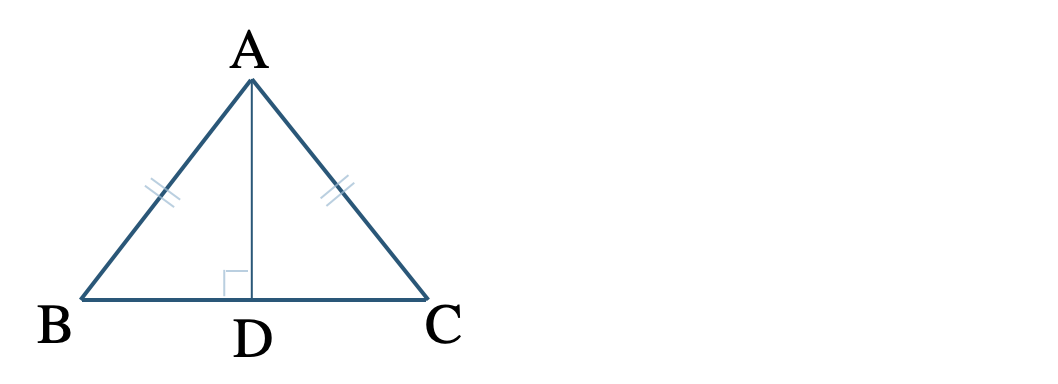
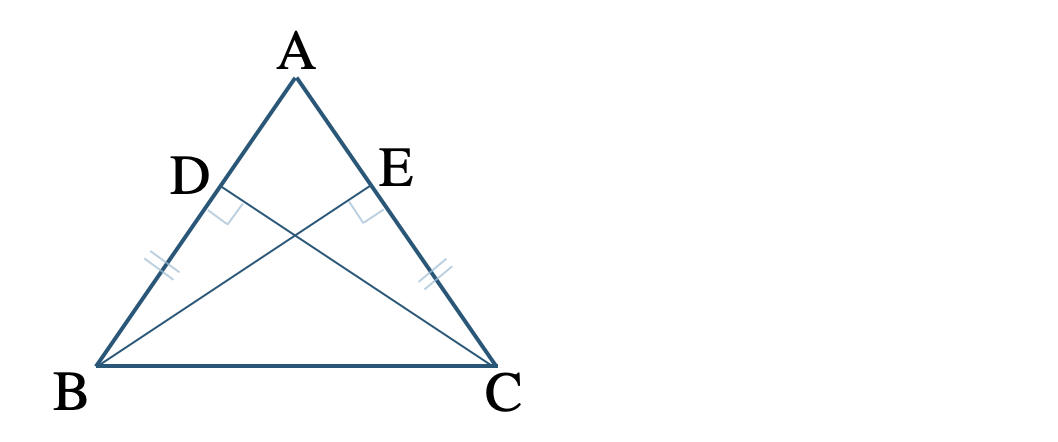
\({\small (2)}~\)\(\triangle {\rm ABC}\) の点 \({\rm B~,~C}\) からそれぞれ辺 \({\rm AC~,~AB}\) に垂線をひき、その交点を \({\rm E~,~D}\) とするとき、\({\rm BD=CE}\) ならば \(\triangle {\rm ABC}\) が二等辺三角形となることを証明せよ。
\({\small (3)}~\)次の図において、点 \({\rm P}\) から直線 \({\rm OX~,~OY}\) にそれぞれ垂線をひき、その交点を \({\rm A~,~B}\) とするとき、\({\rm OA=OB}\) ならば直線 \({\rm OP}\) は \(\angle{\rm XOY}\) の二等分線となることを証明せよ。
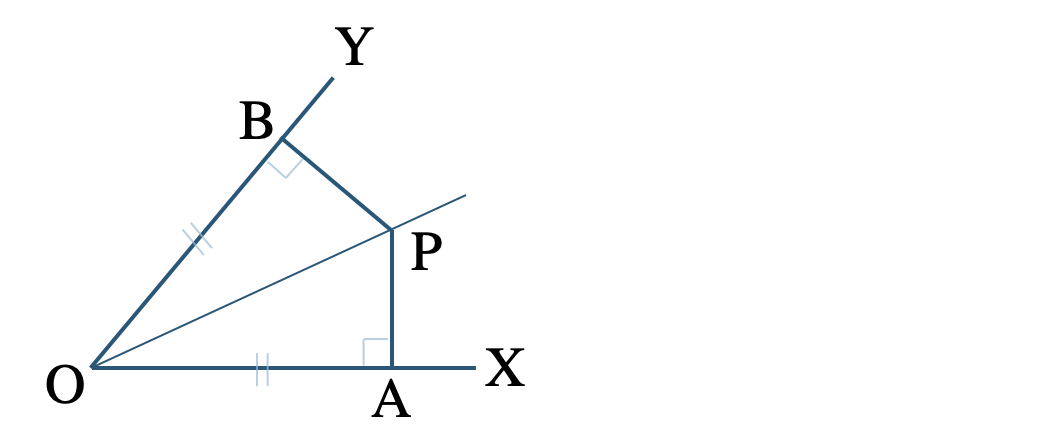
[ 解答を見る ]
【解答】
\({\small (1)}~\)[証明] \(\triangle {\rm ABD}\) と \(\triangle {\rm ACD}\) において、
仮定より、
\({\rm AB=AC}~~~\cdots{\large ①}\)
\(\angle{\rm ADB}=\angle{\rm ADC}=90^\circ~~~\cdots{\large ②}\)
共通の辺より、
\({\rm AD=AD}~~~\cdots{\large ③}\)
①、②、③より、直角三角形の斜辺と他の１辺がそれぞれ等しいから、
\(\triangle {\rm ABD}\equiv\triangle {\rm ACD}\)
合同な図形では対応する辺の長さは等しいから、
\({\rm BD=CD}\)
[終]
\({\small (2)}~\)[証明] \(\triangle {\rm DBC}\) と \(\triangle {\rm ECB}\) において、
仮定より、
\({\rm BD=CE}~~~\cdots{\large ①}\)
\(\angle{\rm BDC}=\angle{\rm CEB}=90^\circ~~~\cdots{\large ②}\)
共通の辺より、
\({\rm BC=CB}~~~\cdots{\large ③}\)
①、②、③より、直角三角形の斜辺と他の１辺がそれぞれ等しいので、
\(\triangle {\rm DBC}\equiv\triangle {\rm ECB}\)
合同な図形では対応する角の大きさは等しいから、
\(\angle{\rm DBC}=\angle{\rm ECB}\)
よって、\(\angle{\rm B}=\angle{\rm C}\) となり、底角が等しいから、
\(\triangle {\rm ABC}\) は二等辺三角形となる
[終]
\({\small (3)}~\)[証明] \(\triangle {\rm POA}\) と \(\triangle {\rm POB}\) において、
仮定より、
\({\rm OA=OB}~~~\cdots{\large ①}\)
\(\angle{\rm PAO}=\angle{\rm PBO}=90^\circ~~~\cdots{\large ②}\)
共通の辺より、
\({\rm PO=PO}~~~\cdots{\large ③}\)
①、②、③より、直角三角形の斜辺と他の１辺がそれぞれ等しいから、
\(\triangle {\rm POA}\equiv\triangle {\rm POB}\)
合同な図形では対応する角の大きさは等しいから、
\(\angle{\rm POA}=\angle{\rm POB}\)
したがって、
直線 \({\rm OP}\) が \(\angle{\rm XOY}\) の二等分線となる
[終]
詳しい解説ページはこちらから↓
平行四辺形の性質
次の問いに答えよ。
\({\small (1)}~\)平行四辺形について、次のことを答えよ。
\(~~{\large ①}~\)平行四辺形の定義を答えよ。
\(~~{\large ②}~\)２組の対辺についての定理を答えよ。
\(~~{\large ③}~\)２組の対角についての定理を答えよ。
\(~~{\large ④}~\)対角線についての定理を答えよ。
\({\small (2)}~\)次の図の ▱ \({\rm ABCD}\) において、次の値を求めよ。
\(~~{\large ①}~\)\({\rm EF\,//\,BC}\) のとき、\(x~,~y\) の値と \(\angle a~,~\angle b\) の大きさを求めよ。
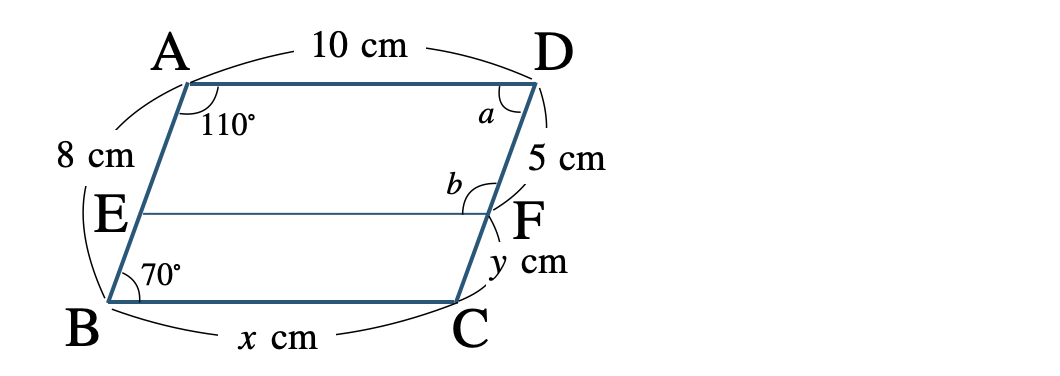
\(~~{\large ②}~\)対角線 \({\rm AC~,~BD}\) の交点を \({\rm O}\) とするとき、\(x~,~y\) の値を求めよ。
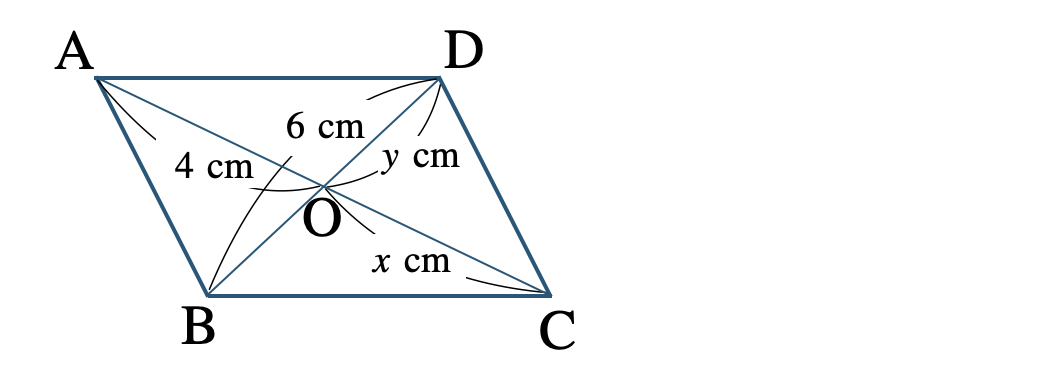
[ 解答を見る ]
【解答】
\({\small (1)}~\)
\(~~{\large ①}~\)２組の対辺がそれぞれ平行な四角形を平行四辺形という
\(~~{\large ②}~\)平行四辺形の対辺はそれぞれ等しい
\(~~{\large ③}~\)平行四辺形の対角はそれぞれ等しい
\(~~{\large ④}~\)平行四辺形の対角線はそれぞれの中点で交わる
\({\small (2)}~\)$$~~{\large ①}~x=10~{\rm cm}~,~y=3~{\rm cm}~,~a=70^\circ~,~b=110^\circ$$$$~~{\large ②}~x=4~{\rm cm}~,~y=3~{\rm cm}$$
詳しい解説ページはこちらから↓
平行四辺形の証明
次の証明をせよ。
\({\small (1)}~\)平行四辺形の定理１と定理２を、対角線 \({\rm AC}\) をひくことで証明せよ。
【定理１】平行四辺形の対辺はそれぞれ等しい
【定理２】平行四辺形の対角はそれぞれ等しい
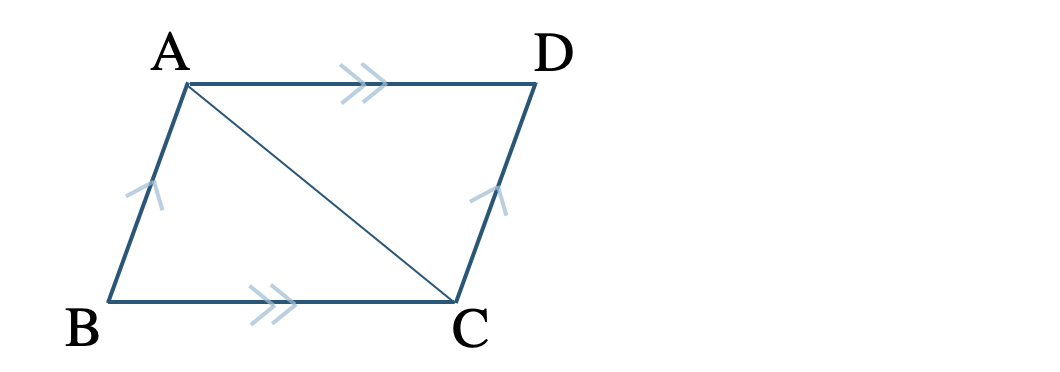
\({\small (2)}~\)平行四辺形の定理３を、対角線 \({\rm AC~,~BD}\) の交点 \({\rm O}\) をすることで証明せよ。
【定理３】平行四辺形の対角線はそれぞれの中点で交わる
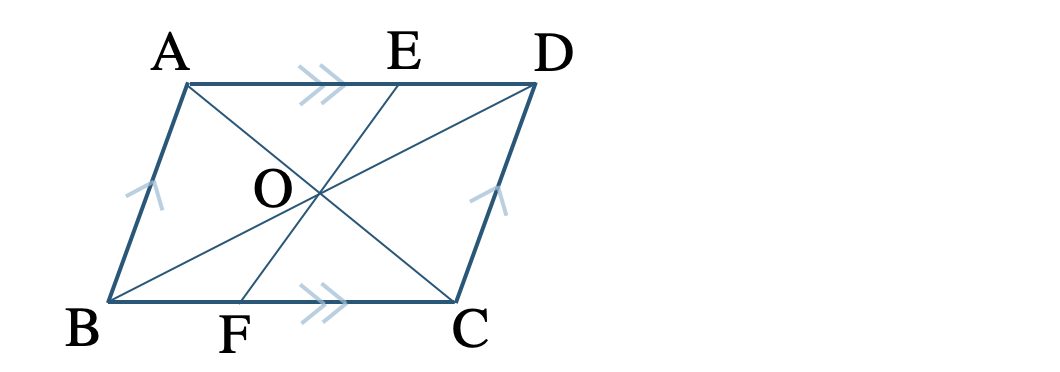
\({\small (3)}~\)▱ \({\rm ABCD}\)の対角線 \({\rm AC~,~BD}\) との交点を \({\rm O}\) として、この交点 \({\rm O}\) を通る直線と辺 \({\rm AD~,~BC}\) との交点を \({\rm E~,~F}\) とするとき、\({\rm OE=OF}\) であることを証明せよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)[証明] \(\triangle {\rm ABC}\) と \(\triangle {\rm CDA}\) において、
\({\rm AD\,//\,BC}\) より、錯角が等しいので、
\(\angle{\rm ACB}=\angle{\rm CAD}~~~\cdots{\large ①}\)
\({\rm AB\,//\,DC}\) より、錯角が等しいので、
\(\angle{\rm BAC}=\angle{\rm DCA}~~~\cdots{\large ②}\)
共通の辺より、
\({\rm AC=CA}~~~\cdots{\large ③}\)
①、②、③より、１組の辺とその両端の角がそれぞれ等しいから、
\(\triangle {\rm ABC}\equiv\triangle {\rm CDA}\)
合同な図形では対応する辺の長さ、角の大きさは等しいから、
\({\rm AB=CD~,~BC=DA}~~~\cdots{\large ④}\)
\(\angle{\rm ABC}=\angle{\rm CDA}~~~\cdots{\large ⑤}\)
④より、\({\rm AB=CD~,~AD=BC}\) となるので、
【定理１】平行四辺形の対辺はそれぞれ等しい
が示される
また、①と②より、$$\begin{eqnarray}~~~\angle{\rm BAC}+\angle{\rm DAC}&=&\angle{\rm ACD}+\angle{\rm DCA}\\[2pt]~~~\angle{\rm BAD}&=&\angle{\rm DCB}\\[2pt]~~~\angle{\rm A}&=&\angle{\rm C}\end{eqnarray}$$⑤より、\(\angle{\rm B}=\angle{\rm D}\) となるので、
【定理２】平行四辺形の対角はそれぞれ等しい
が示される [終]
\({\small (2)}~\)[証明] \(\triangle {\rm AOB}\) と \(\triangle {\rm COB}\) において、
平行四辺形の対辺は等しいので、
\({\rm AB=CD}~~~\cdots{\large ①}\)
平行四辺形の定義 \({\rm AB\,//\,DC}\) より、錯角が等しいので、
\(\angle{\rm BAO}=\angle{\rm DCO}~~~\cdots{\large ②}\)
\(\angle{\rm ABO}=\angle{\rm CDO}~~~\cdots{\large ③}\)
①、②、③より、１組の辺とその両端の角がそれぞれ等しいから、
\(\triangle {\rm AOB}\equiv\triangle {\rm COD}\)
合同な図形では対応する辺の長さは等しいから、
\({\rm AO=CO~,~BO=DO}\)
したがって、
【定理３】平行四辺形の対角線はそれぞれの中点で交わる
[終]
\({\small (3)}~\)[証明] \(\triangle {\rm OBF}\) と \(\triangle {\rm ODE}\) において、
仮定より、
\({\rm BF=DF}~~~\cdots{\large ①}\)
平行四辺形の対角線はそれぞれの中点で交わるので、
\({\rm OB=OD}~~~\cdots{\large ②}\)
平行四辺形の定義 \({\rm BC\,//\,AD}\) より、錯角が等しいので、
\(\angle{\rm OBF}=\angle{\rm ODE}~~~\cdots{\large ③}\)
①、②、③より、２組の辺とその間の角がそれぞれ等しいから、
\(\triangle {\rm OBF}\equiv\triangle {\rm ODE}\)
合同な図形では対応する辺の長さは等しいから、
\({\rm OE=OF}\)
[終]
詳しい解説ページはこちらから↓
平行四辺形になるための条件
次の問いに答えよ。
\({\small (1)}~\)四角形 \({\rm ABCD}\) で、
\({\rm AB=DC~,~AD=BC}\) ならば
四角形 \({\rm ABCD}\) は平行四辺形である
ことを証明せよ。
\({\small (2)}~\)四角形 \({\rm ABCD}\) で、
\(\angle{\rm A}=\angle{\rm C}~,~\angle{\rm B}=\angle{\rm D}\) ならば
四角形 \({\rm ABCD}\) は平行四辺形である
ことを証明せよ。
\({\small (3)}~\)四角形 \({\rm ABCD}\) で対角線の交点を \({\rm O}\) とするとき、
\({\rm AO=CO~,~BO=DO}\) ならば
四角形 \({\rm ABCD}\) は平行四辺形である
ことを証明せよ。
\({\small (4)}~\)四角形 \({\rm ABCD}\) で、
\({\rm AD=BC~,~AD\,//\,BC}\) ならば
四角形 \({\rm ABCD}\) は平行四辺形である
ことを証明せよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)[証明] 対角線 \({\rm AC}\) をひき、\(\triangle {\rm ABC}\) と \(\triangle {\rm ABC}\) において、
仮定より、
\({\rm AB=CD}~~~\cdots{\large ①}\)
\({\rm BC=DA}~~~\cdots{\large ②}\)
共通の辺より、
\({\rm AC=CA}~~~\cdots{\large ③}\)
①、②、③より、３組の辺がそれぞれ等しいから、
\(\triangle {\rm ABC}\equiv\triangle {\rm CDA}\)
合同な図形では対応する角の大きさは等しいから、
\(\angle{\rm BAC}=\angle{\rm DCA}~~~\cdots{\large ④}\)
\(\angle{\rm ACB}=\angle{\rm CAD}~~~\cdots{\large ⑤}\)
④より、錯角が等しいので \({\rm AB\,//\,CD}\)
⑤より、錯角が等しいので \({\rm AD\,//\,BC}\)
対辺がそれぞれ平行であるので、
四角形 \({\rm ABCD}\) は平行四辺形である
[終]
\({\small (2)}~\)[証明] 辺 \({\rm BC}\) の延長線上の点を \({\rm E}\) とする
四角形の内角の和が \(360^\circ\) より、$$~~~\angle{\rm A}+\angle{\rm B}+\angle{\rm C}+\angle{\rm D}=360^\circ$$\(\angle{\rm A}=\angle{\rm C}~,~\angle{\rm B}=\angle{\rm D}\) であるので、$$\begin{eqnarray}~~~\angle{\rm A}+\angle{\rm B}+\angle{\rm C}+\angle{\rm D}&=&360^\circ\\[2pt]~~~\angle{\rm C}+\angle{\rm D}+\angle{\rm C}+\angle{\rm D}&=&360^\circ\\[2pt]~~~2(\angle{\rm C}+\angle{\rm D})&=&360^\circ\\[2pt]~~~\angle{\rm C}+\angle{\rm D}&=&180^\circ\end{eqnarray}$$これより、$$~~~\angle{\rm DCE}=180^\circ-\angle{\rm C}=\angle{\rm D}$$錯角が等しいので、
\({\rm AD\,//\,BC}~~~\cdots{\large ①}\)
同様に考えて、
\({\rm AB\,//\,DC}~~~\cdots{\large ②}\)
①と②より、対辺がそれぞれ平行であるので、
四角形 \({\rm ABCD}\) は平行四辺形である
[終]
\({\small (3)}~\)[証明] \(\triangle {\rm ABO}\) と \(\triangle {\rm CDO}\) において、
仮定より、
\({\rm AO=CO}~~~\cdots{\large ①}\)
\({\rm BO=DO}~~~\cdots{\large ②}\)
対頂角が等しいので、
\(\angle{\rm AOB}=\angle{\rm COD}~~~\cdots{\large ③}\)
①、②、③より、２組の辺とその間の角がそれぞれ等しいから、
\(\triangle {\rm ABO}\equiv\triangle {\rm CDO}\)
合同な図形では対応する角の大きさは等しいから、
\(\angle{\rm BAO}=\angle{\rm DCO}\)
錯角が等しいので、
\({\rm AB\,//\,DC}\)
\(\triangle {\rm AOD}\) と \(\triangle {\rm COB}\) でも同様に考えて、
\({\rm AD\,//\,BC}\)
対辺がそれぞれ平行であるので、
四角形 \({\rm ABCD}\) は平行四辺形である
[終]
\({\small (4)}~\)[証明] 対角線 \({\rm AC}\) をひき、\(\triangle {\rm ABC}\) と \(\triangle {\rm ABC}\) において、
仮定より、
\({\rm BC=DA}~~~\cdots{\large ①}\)
\({\rm BC\,//\,AD}\) より、錯角が等しいので、
\(\angle{\rm ACB}=\angle{\rm CAD}~~~\cdots{\large ②}\)
共通の辺より、
\({\rm AC=CA}~~~\cdots{\large ③}\)
①、②、③より、２組の辺とその間の角がそれぞれ等しいから、
\(\triangle {\rm ABC}\equiv\triangle {\rm CDA}\)
合同な図形では対応する角の大きさは等しいから、
\(\angle{\rm BAC}=\angle{\rm DCA}\)
錯角が等しいので \({\rm AB\,//\,CD}\)
したがって、対辺がそれぞれ平行であるので、
四角形 \({\rm ABCD}\) は平行四辺形である
[終]
詳しい解説ページはこちらから↓
辺や角の条件と平行四辺形
次の四角形 \({\rm ABCD}\) が平行四辺形であるか調べよ。
\({\small (1)}~\)\(\angle{\rm A}=\angle{\rm B}~,~\angle{\rm C}=\angle{\rm D}\)
\({\small (2)}~\)\({\rm AB=CD~,~AD=BC}\)
\({\small (3)}~\)\(\angle{\rm A}=\angle{\rm C}~,~\angle{\rm B}=\angle{\rm D}\)
\({\small (4)}~\)\({\rm AD=BC~,~AB\,//\,CD}\)
\({\small (5)}~\)\({\rm AB=BC~,~AD=CD}\)
\({\small (6)}~\)\({\rm AD=BC~,~}\)\(\angle{\rm A}=60^\circ~,~\angle{\rm B}=120^\circ\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)四角形 \({\rm ABCD}\) は平行四辺形でない
\({\small (2)}~\)四角形 \({\rm ABCD}\) は平行四辺形である
\({\small (3)}~\)四角形 \({\rm ABCD}\) は平行四辺形である
\({\small (4)}~\)四角形 \({\rm ABCD}\) は平行四辺形でない
\({\small (5)}~\)四角形 \({\rm ABCD}\) は平行四辺形でない
\({\small (6)}~\)四角形 \({\rm ABCD}\) は平行四辺形である
詳しい解説ページはこちらから↓
図形の中の平行四辺形
次の証明をせよ。
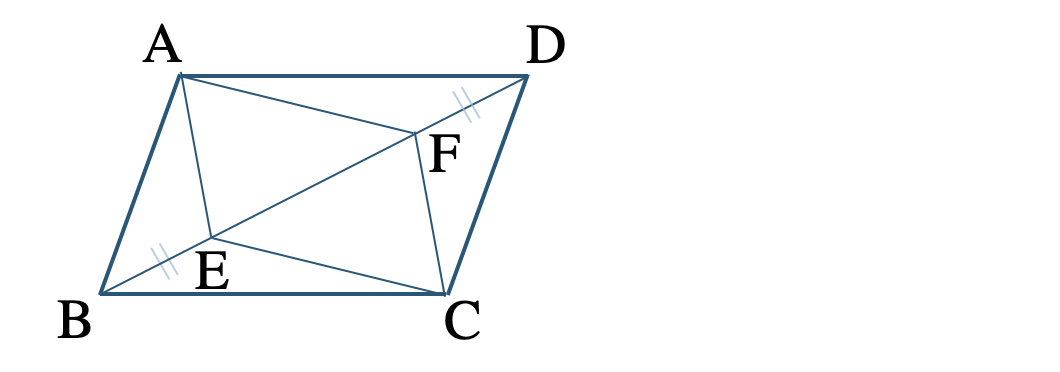
\({\small (1)}~\)▱ \({\rm ABCD}\) の対角線 \({\rm BD}\) 上に、\({\rm BE=DF}\) となるように点 \({\rm E~,~F}\) をとる。
このとき、四角形 \({\rm AECF}\) が平行四辺形となることを示せ。
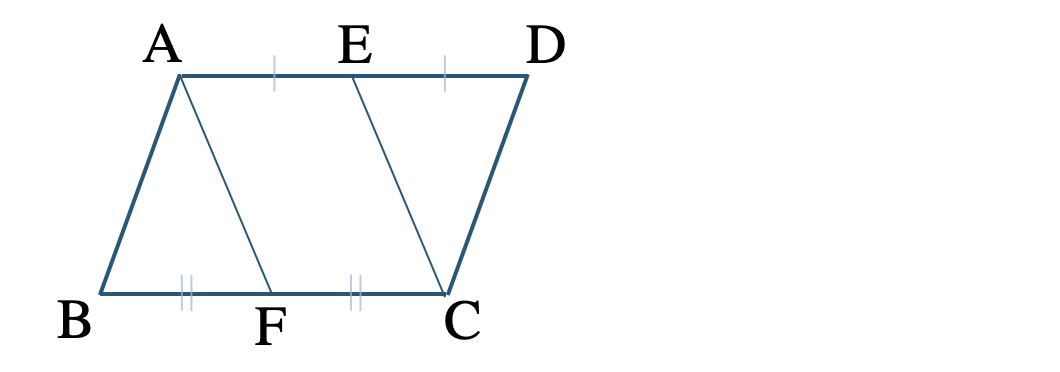
\({\small (2)}~\)▱ \({\rm ABCD}\) について、辺 \({\rm AD~,~BC}\) の中点をそれぞれ \({\rm E~,~F}\) とする。
このとき、四角形 \({\rm AFCE}\) が平行四辺形となることを示せ。
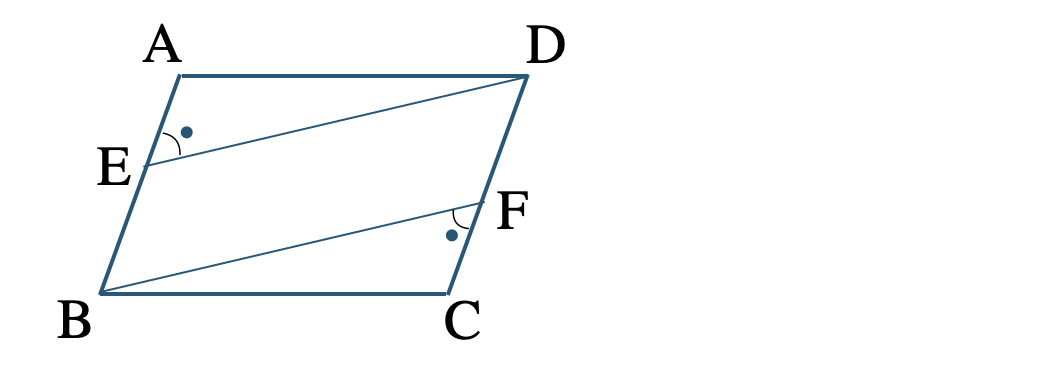
\({\small (3)}~\)▱ \({\rm ABCD}\) の辺 \({\rm AB~,~CD}\) 上に \(\angle{\rm AED}=\angle{\rm CFB}\) となるように点 \({\rm E~,~F}\) をとる。
このとき、四角形 \({\rm EBFD}\) が平行四辺形となることを示せ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)[証明] 対角線の交点を \({\rm O}\) として、▱ \({\rm ABCD}\) の対角線がそれぞれの中点で交わるので、
\({\rm AO=CO}~~~\cdots{\large ①}\)
\({\rm BO=DO}~~~\cdots{\large ②}\)
仮定より、
\({\rm BE=DF}~~~\cdots{\large ③}\)
②と③より、$$\begin{eqnarray}~~~{\rm BO-BE}&=&{\rm DO-DF}\\[2pt]~~~{\rm EO}&=&{\rm FO}~~~\cdots{\large ④}\end{eqnarray}$$①と④より、対角線がそれぞれの中点で交わるので、
四角形 \({\rm AECF}\) が平行四辺形となる
[終]
\({\small (2)}~\)[証明] ▱ \({\rm ABCD}\) の対辺は平行で長さが等しいので、
\({\rm AD\,//\,BC}~~~\cdots{\large ①}\)
\({\rm AD=BC}~~~\cdots{\large ②}\)
①より、
\({\rm AE\,//\,FC}~~~\cdots{\large ③}\)
仮定より、点 \({\rm E~,~F}\) は辺 \({\rm AD~,~BC}\) の中点であるので、$$~~~{\rm AE}=\frac{\,1\,}{\,2\,}{\rm AD}~,~{\rm FC}=\frac{\,1\,}{\,2\,}{\rm BC}$$これと②より、
\({\rm AE=FC}~~~\cdots{\large ④}\)
③と④より、１組の対辺が等しくて平行であるので、
四角形 \({\rm AFCE}\) が平行四辺形となる
[終]
\({\small (3)}~\)[証明] ▱ \({\rm ABCD}\) の２組の対角がそれぞれ等しいので、
\(\angle{\rm EAD}=\angle{\rm FCB}~~~\cdots{\large ①}\)
\(\angle{\rm ADC}=\angle{\rm CBA}~~~\cdots{\large ②}\)
仮定より、
\(\angle{\rm AED}=\angle{\rm CFB}~~~\cdots{\large ③}\)
①と③より、三角形の内角の和が \(180^\circ\) であるので、
\(\angle{\rm ADE}=\angle{\rm CBF}\)
これと②より、
\(\angle{\rm EDF}=\angle{\rm FBE}~~~\cdots{\large ④}\)
また、③より、
\(\angle{\rm DEB}=\angle{\rm BFD}~~~\cdots{\large ⑤}\)
④と⑤より、２組の対角がそれぞれ等しいので、
四角形 \({\rm EBFD}\) が平行四辺形となる
[終]
詳しい解説ページはこちらから↓
特別な平行四辺形
次の問いに答えよ。
\({\small (1)}~\)四角形 \({\rm ABCD}\) が長方形であるとき、
\({\rm AC=BD}\)
であることを証明せよ。
\({\small (2)}~\)四角形 \({\rm ABCD}\) がひし形であるとき、対角線の交点を \({\rm O}\) として、
\({\rm AC\perp BD}\)
であることを証明せよ。
\({\small (3)}~\)次の図において、
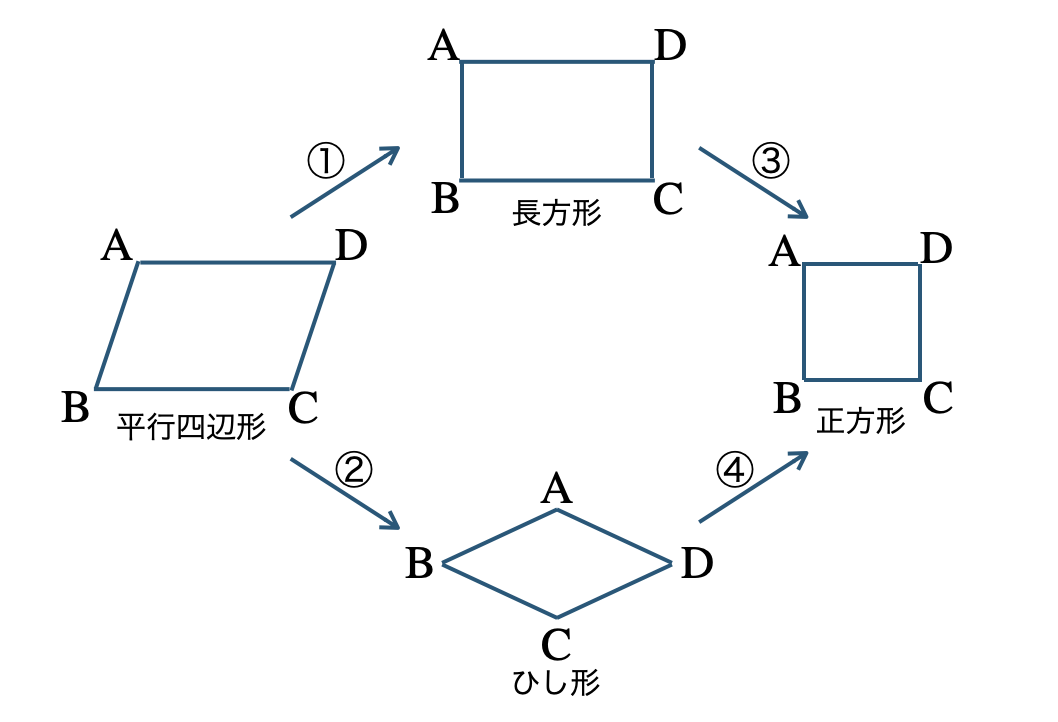
①〜④にはどのような条件を加えればよいか、以下よりすべて選べ。$$\begin{split}~~~&\angle{\rm A}=\angle{\rm B}~,~{\rm AB=BC}\\[2pt]~~~&{\rm AC=BD}~,~{\rm AC\perp BD}~,~\angle{\rm A}=90^\circ\end{split}$$
[ 解答を見る ]
【解答】
\({\small (1)}~\)[証明] \(\triangle {\rm ABC}\) と \(\triangle {\rm DCB}\) について、
長方形の定義より、
\(\angle{\rm ABC}=\angle{\rm DCB}~~~\cdots{\large ①}\)
長方形は平行四辺形でもあり、対辺が等しいので、
\({\rm AB=DC}~~~\cdots{\large ②}\)
共通の辺より、
\({\rm BC=CB}~~~\cdots{\large ③}\)
①、②、③より、２組の辺とその間の角がそれぞれ等しいので、
\(\triangle {\rm ABC}\equiv\triangle {\rm DCB}\)
合同な図形では対応する辺の長さは等しいから、
\({\rm AC=DB}\)
したがって、
\({\rm AC=BD}\)
[終]
\({\small (2)}~\)[証明] \(\triangle {\rm ABO}\) と \(\triangle {\rm ADO}\) について、
ひし形の定義より、
\({\rm AB=AD}~~~\cdots{\large ①}\)
ひし形は平行四辺形でもあり、対角線がそれぞれの中点で交わるので、
\({\rm BO=DO}~~~\cdots{\large ②}\)
共通の辺より、
\({\rm AO=AO}~~~\cdots{\large ③}\)
①、②、③より、３組の辺がそれぞれ等しいので、
\(\triangle {\rm ABO}\equiv\triangle {\rm ADO}\)
合同な図形では対応する角の大きさは等しいから、
\(\angle{\rm BAO}=\angle{\rm DAO}\)
これより、\(\triangle {\rm ABD}\) は二等辺三角形であり、線分 \({\rm AO}\) は \(\angle{\rm }\) の二等分線である
二等辺三角形の頂角の二等分線は、底辺を垂直に二等分するので、
\({\rm AO\perp BD}\)
したがって、
\({\rm AB\perp BD}\)
[終]
\({\small (3)}~\)$$~~{\large ①}~\angle{\rm A}=\angle{\rm B}~,~{\rm AC=BD}~,~\angle{\rm A}=90^\circ$$$$~~{\large ②}~{\rm AB=BC~,~AC\perp BD}$$$$~~{\large ③}~{\rm AB=BC~,~AC\perp BD}$$$$~~{\large ④}~\angle{\rm A}=\angle{\rm B}~,~{\rm AC=BD}~,~\angle{\rm A}=90^\circ$$
詳しい解説ページはこちらから↓
平行線と面積
次の問いに答えよ。
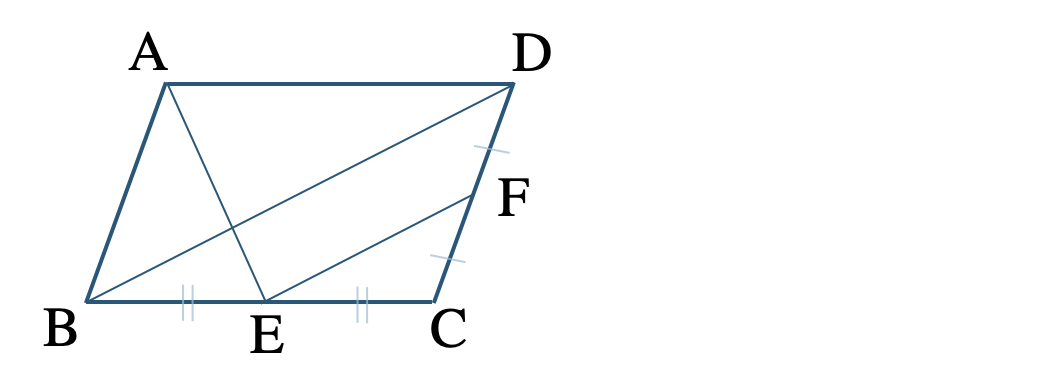
\({\small (1)}~\)▱ \({\rm ABCD}\) で辺 \({\rm BC~,~CD}\) の中点をそれぞれ \({\rm E~,~F}\) として \({\rm BD\,//\,EF}\) であるとき、\(\triangle {\rm ABE}\) と同じ面積の三角形をすべて答えよ。
\({\small (2)}~\)四角形 \({\rm ABCD}\) で \({\rm AD\,//\,BC}\) であり、対角線 \({\rm AC~,~BD}\) の交点を \({\rm O}\) とするとき、\(\triangle {\rm ABO}=\triangle {\rm DCO}\) であることを証明せよ。
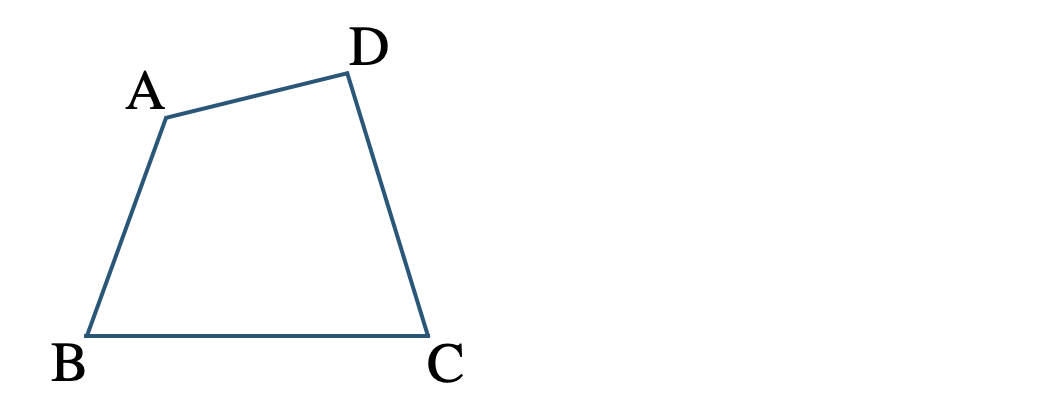
\({\small (3)}~\)図の四角形 \({\rm ABCD}\) の面積を変えずに三角形にするにはどのようにすればよいか答えよ。
\({\small (4)}~\)長方形 \({\rm ABCD}\) が境界線で２つの部分①、②に分けられる。
①と②の面積を変えずに、点 \({\rm E}\) を通る直線で境界線をひきなおすとき、どのようにひけばよいか答えよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
\(\triangle {\rm DBE}~,~\triangle {\rm DEC}~,~\triangle {\rm AEC}~,~\triangle {\rm DBF}\)
\(~,~\triangle {\rm AFD}~,~\triangle {\rm ACF}~,~\triangle {\rm BCF}\)
\({\small (2)}~\)[証明] \({\rm AD\,//\,BC}\) より、\({\rm BC}\) を底辺とする三角形について、
\(\triangle {\rm ABC}=\triangle {\rm DBC}\)
ここで、
\(\triangle {\rm ABC}=\triangle {\rm ABO}+\triangle {\rm OBC}\)
\(\triangle {\rm DBC}=\triangle {\rm DOC}+\triangle {\rm OBC}\)
\(\triangle {\rm OBC}\) が共通しているので、
\(\triangle {\rm ABO}=\triangle {\rm DOC}\)
[終]
\({\small (3)}~\)対角線 \({\rm AC}\) をひき、これに平行で点 \({\rm D}\) を通る直線をひく
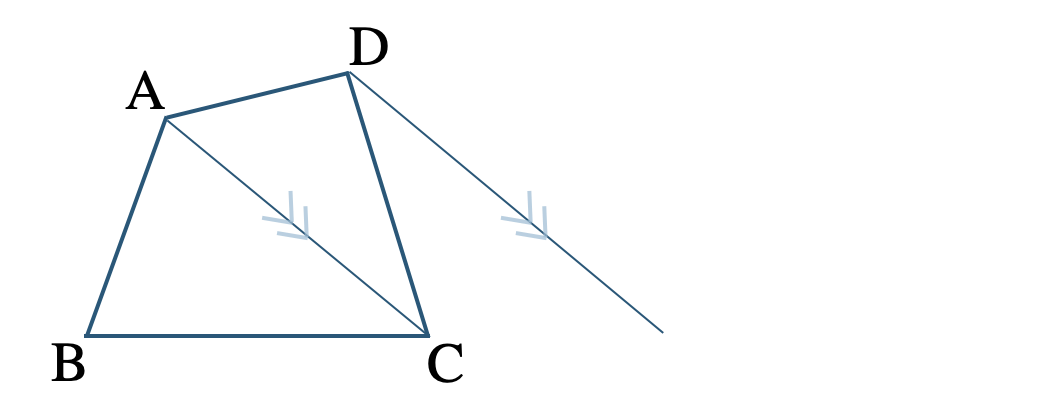
この平行線と辺 \({\rm BC}\) の延長線との交点を \({\rm E}\) とする
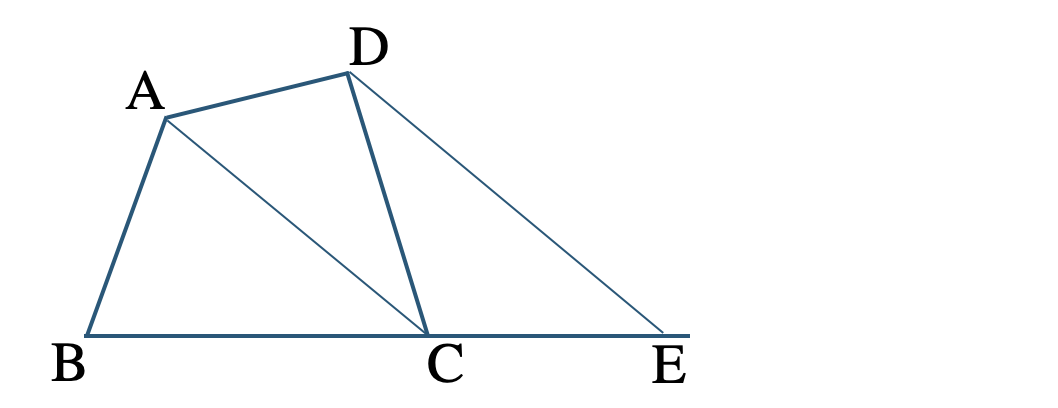
線分 \({\rm AE}\) をひくと、\({\rm AC\,//\,DE}\) より、
\(\triangle {\rm ACD}=\triangle {\rm ACE}\)
となるので、
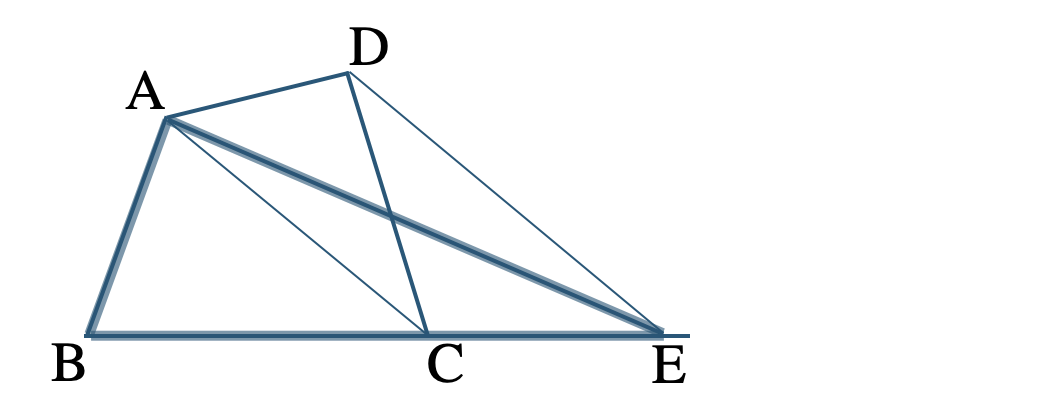
\(\triangle {\rm ABE}\) がもとの四角形 \({\rm ABCD}\) と面積が等しくなる
\({\small (4)}~\)線分 \({\rm EF}\) をひき、これに平行で点 \({\rm G}\) を通る直線をひく
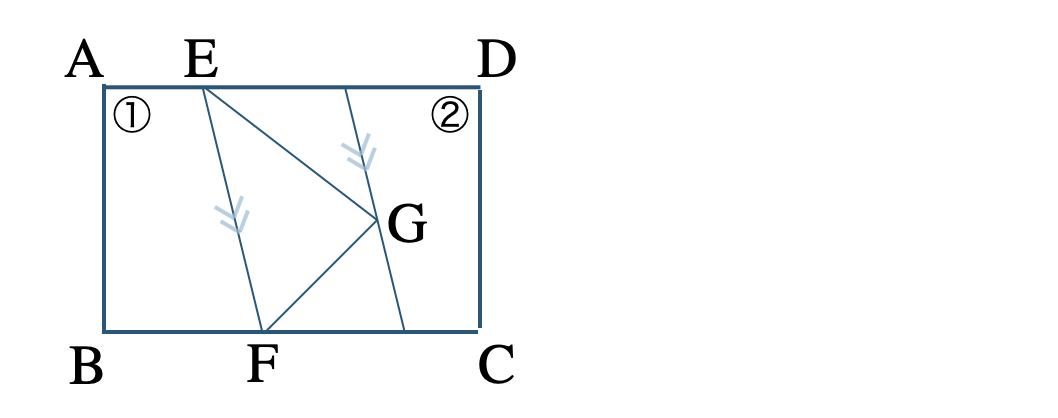
この平行線と辺 \({\rm BC}\) との交点を \({\rm H}\) とする
\({\rm EH}\) をひくと \({\rm EF\,//\,GH}\) より、
\(\triangle {\rm EFG}=\triangle {\rm EFH}\)
となる
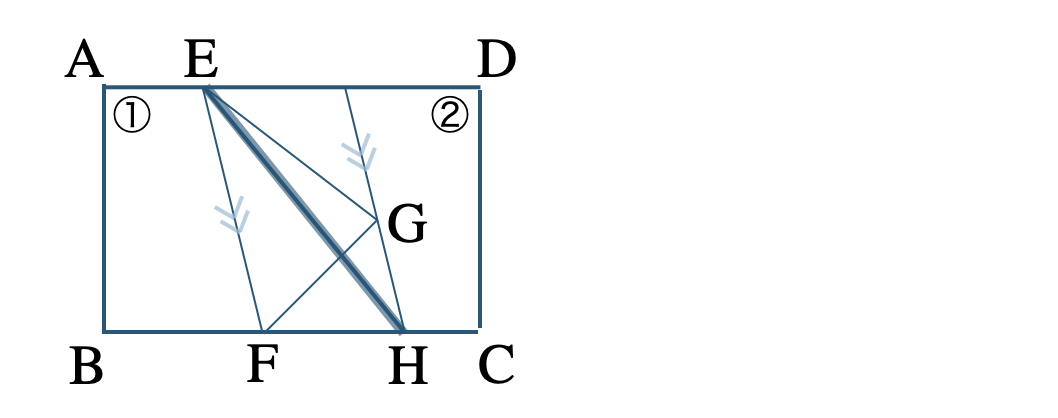
したがって、
線分 \({\rm EH}\) によって、①と②の面積を変えずに境界線をひきなおせる
詳しい解説ページはこちらから↓
