【ご注意ください】このページの内容について
このページは、旧版教科書に基づいて作成された内容です。
現在の教科書とは一部内容や表現が異なる場合があります。
順次、最新版に対応したページへと更新を進めておりますので、ご了承ください。
このページは、数研出版:これからの数学1
6章 空間図形
6章 空間図形

教科書に完全対応の問題集|教科書ぴったりトレーニング
教科書に対応した数学の問題集|教科書ぴったりトレーニングの紹介 こんにちは、みなさん!今回は中学生の...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
数研出版中1 1章 正の数と負の数(令和7年度対応)
数研出版中1 2章 文字と式(令和7年度対応)
数研出版中1 3章 1次方程式(令和7年度対応)
数研出版中1 4章 比例と反比例(令和7年度対応)
数研出版中1 5章 平面図形(令和7年度対応)
数研出版中1 6章 空間図形
数研出版中1 7章 データの活用
6章 空間図形
1 空間図形
1 いろいろな立体
p.189 問1 エ:五面体 カ:六面体 キ:四面体
■ 同じタイプの例題解説
» いろいろな立体
» いろいろな立体
p.190 問2\({\small (1)}~\)底面が六角形で2つ
\(~~~~~\)側面が長方形で6つ
\({\small (2)}~\)底面が正五角形で1つ
\(~~~~~\)側面が二等辺三角形で5つ
\(~~~~~\)側面が長方形で6つ
\({\small (2)}~\)底面が正五角形で1つ
\(~~~~~\)側面が二等辺三角形で5つ
■ 同じタイプの例題解説
» いろいろな立体
» いろいろな立体
p.190 問3\(~~~\)②
■ 同じタイプの例題解説
» いろいろな立体
» いろいろな立体
p.190 問4\({\small (1)}~\)
・同じであること
\(~~~\)底面の形が正方形、側面の数が4つ
・異なっていること
\(~~~\)底面の数、側面の形
\({\small (2)}~\)
・同じであること
\(~~~\)底面の形が円
・異なっていること
\(~~~\)底面の数、側面の形
・同じであること
\(~~~\)底面の形が正方形、側面の数が4つ
・異なっていること
\(~~~\)底面の数、側面の形
\({\small (2)}~\)
・同じであること
\(~~~\)底面の形が円
・異なっていること
\(~~~\)底面の数、側面の形
■ 同じタイプの例題解説
» いろいろな立体
» いろいろな立体
p.191 問5\({\small (1)}~\)
\(~~~\)正四面体:正三角形
\(~~~\)正六面体:正方形
\(~~~\)正八面体:正三角形
\(~~~\)正十二面体:正五角形
\(~~~\)正二十面体:正三角形
\({\small (2)}~\)
\(~~~\)正四面体:\(3\)
\(~~~\)正六面体:\(3\)
\(~~~\)正八面体:\(4\)
\(~~~\)正十二面体:\(3\)
\(~~~\)正二十面体:\(5\)
\(~~~\)正四面体:正三角形
\(~~~\)正六面体:正方形
\(~~~\)正八面体:正三角形
\(~~~\)正十二面体:正五角形
\(~~~\)正二十面体:正三角形
\({\small (2)}~\)
\(~~~\)正四面体:\(3\)
\(~~~\)正六面体:\(3\)
\(~~~\)正八面体:\(4\)
\(~~~\)正十二面体:\(3\)
\(~~~\)正二十面体:\(5\)
■ 同じタイプの例題解説
» 正多面体
» 正多面体
p.191 問6正多面体の性質「どの頂点にも同じ数の面が集まる」をもたない
■ 同じタイプの例題解説
» 正多面体
» 正多面体
2 空間における平面と直線
p.193 問1異なる3点がつくる平面上にもう1つの点がないとき
p.194 問3\(~~~\)3本(直線BE、DE、EF)
■ 同じタイプの例題解説
» 空間内の2直線
» 空間内の2直線
p.195 問4\({\small (1)}~\)直線AB、BC、AC
\({\small (2)}~\)直線AD、BE、CF
\({\small (3)}~\)直線CF
\({\small (2)}~\)直線AD、BE、CF
\({\small (3)}~\)直線CF
■ 同じタイプの例題解説
» 直線と平面の位置関係
» 直線と平面の位置関係
p.196 問5\({\small (1)}~\)面EFGH
\({\small (2)}~\)面AEFB、BFGC、
\(~~~~~\)CGHD、AEHD
\({\small (2)}~\)面AEFB、BFGC、
\(~~~~~\)CGHD、AEHD
■ 同じタイプの例題解説
» 2つの平面の位置関係
» 2つの平面の位置関係
p.196 問6\(\begin{split}{\small (1)}~45^\circ\end{split}\) \(\begin{split}{\small (2)}~90^\circ\end{split}\)
■ 同じタイプの例題解説
» 2つの平面の位置関係
» 2つの平面の位置関係
3 立体のいろいろな見方
p.198 問1\(\begin{split}{\small (1)}~3~{\rm cm}\end{split}\) \(\begin{split}{\small (2)}~7~{\rm cm}\end{split}\)
■ 同じタイプの例題解説
» 直線と平面の位置関係
» 直線と平面の位置関係
p.199 問2\(~~~\)正三角柱の側面
■ 同じタイプの例題解説
» 面や線が動いてできる立体
» 面や線が動いてできる立体
p.200 問3\({\small (1)}~\)回転の軸をふくむ平面
\(~~~\)円柱:長方形、円錐:二等辺三角形
\({\small (2)}~\)回転の軸に垂直な平面
\(~~~\)円柱:円、円錐:円
\(~~~\)円柱:長方形、円錐:二等辺三角形
\({\small (2)}~\)回転の軸に垂直な平面
\(~~~\)円柱:円、円錐:円
■ 同じタイプの例題解説
» 平面の回転体
» 平面の回転体
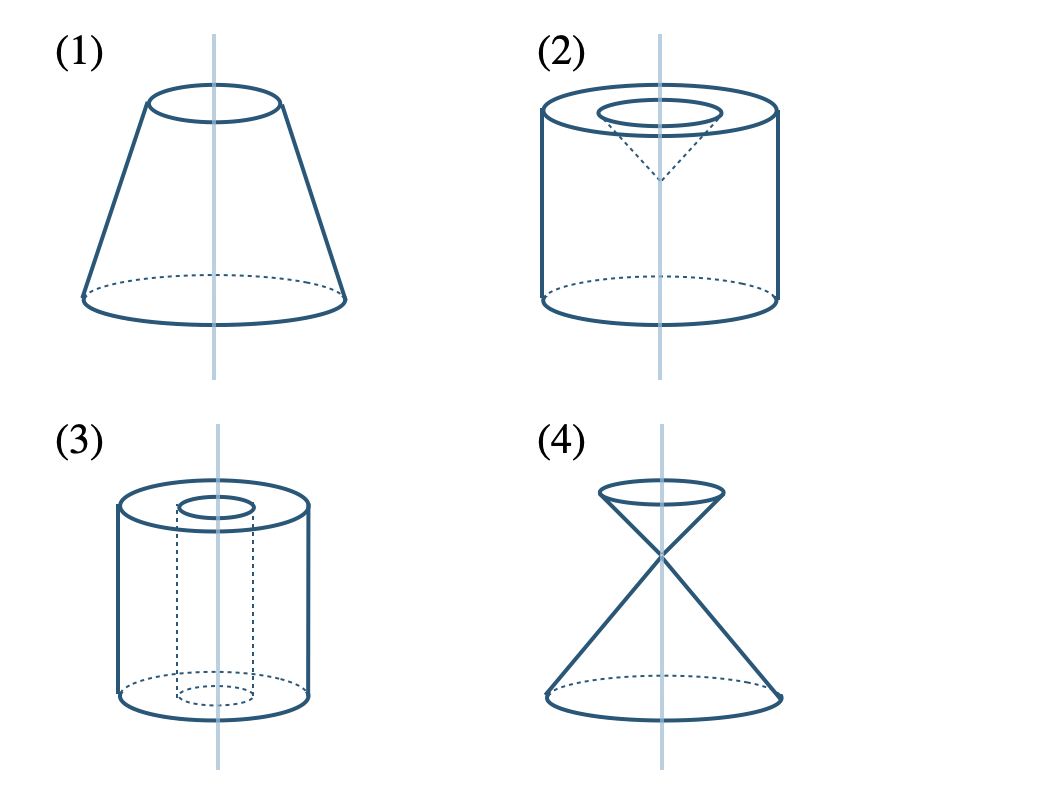
p.201 問4\(~~~\)ウ
■ 同じタイプの例題解説
» 平面の回転体
» 平面の回転体
p.203 問8どちらも投影図では同じ形になるので、これを区別するには側面からの図も必要である
■ 同じタイプの例題解説
» 立体の投影図
» 立体の投影図
2 立体の体積と表面積
1 立体の体積
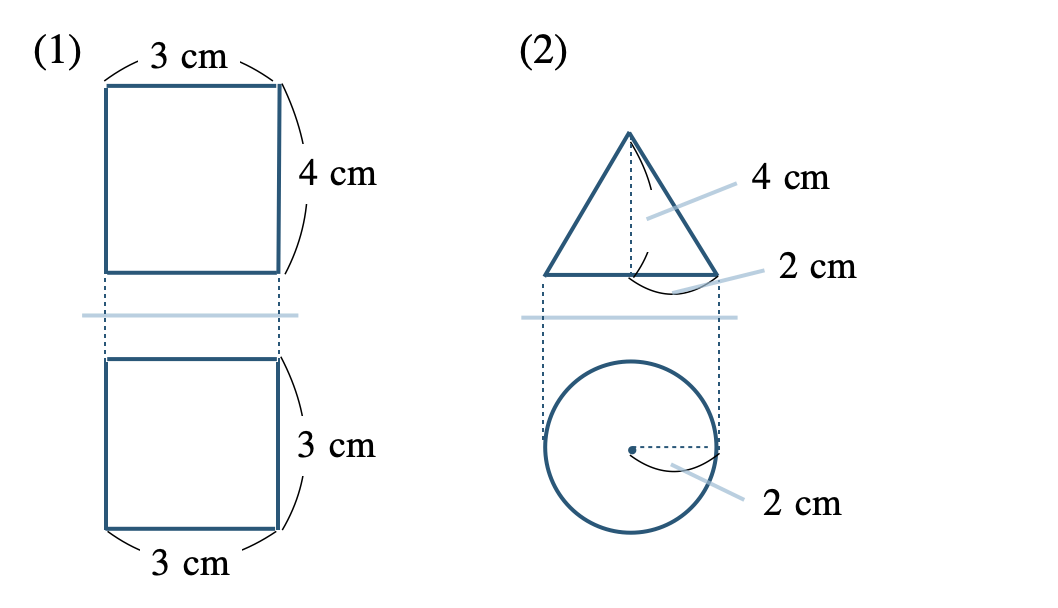
p.206 問1\(\begin{split}{\small (1)}~45~{\rm cm}^3\end{split}\) \(\begin{split}{\small (2)}~96\pi ~{\rm cm}^3\end{split}\)
■ 同じタイプの例題解説
» 立体の体積
» 立体の体積
p.207 問2\(\begin{split}{\small (1)}~50~{\rm cm}^3\end{split}\) \(\begin{split}{\small (2)}~120\pi~{\rm cm}^3\end{split}\)
■ 同じタイプの例題解説
» 立体の体積
» 立体の体積
2 立体の展開図
p.208 問2\(\begin{split}~~~6\pi~{\rm cm}\end{split}\)
■ 同じタイプの例題解説
» 立体の展開図
» 立体の展開図
3 おうぎ形の計量
p.213 問1\({\small (1)}~\)弧の長さ \(6\pi~{\rm cm}\)、面積 \(27\pi~{\rm cm}^2\)
\({\small (2)}~\)弧の長さ \(10\pi~{\rm cm}\)、面積 \(40\pi~{\rm cm}^2\)
\({\small (2)}~\)弧の長さ \(10\pi~{\rm cm}\)、面積 \(40\pi~{\rm cm}^2\)
■ 同じタイプの例題解説
» 円とおうぎ形の計量
» 円とおうぎ形の計量
p.214 問2\(\begin{split}{\small (1)}~12\pi~{\rm cm}^2\end{split}\) \(\begin{split}{\small (2)}~63\pi~{\rm cm}^2\end{split}\)
\(\begin{split}{\small (3)}~130\pi~{\rm cm}^2\end{split}\)
\(\begin{split}{\small (3)}~130\pi~{\rm cm}^2\end{split}\)
■ 同じタイプの例題解説
» 円とおうぎ形の計量
» 円とおうぎ形の計量
p.215 問3\(\begin{split}~~~150^\circ\end{split}\)
■ 同じタイプの例題解説
» 円とおうぎ形の計量
» 円とおうぎ形の計量
4 立体の表面積
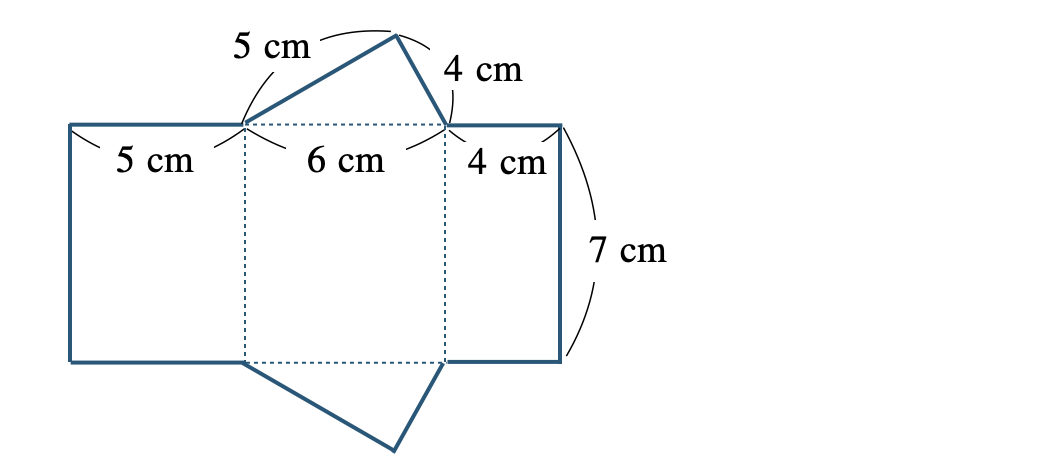
p.216 問1\(\begin{split}{\small (1)}~236~{\rm cm}^2\end{split}\) \(\begin{split}{\small (2)}~120~{\rm cm}^2\end{split}\)
■ 同じタイプの例題解説
» 立体の表面積
» 立体の表面積
p.216 問2\(\begin{split}{\small (1)}~9\pi~{\rm cm}^2\end{split}\) \(\begin{split}{\small (2)}~30\pi~{\rm cm}^2\end{split}\)
\(\begin{split}{\small (3)}~48\pi~{\rm cm}^2\end{split}\)
\(\begin{split}{\small (3)}~48\pi~{\rm cm}^2\end{split}\)
■ 同じタイプの例題解説
» 立体の表面積
» 立体の表面積
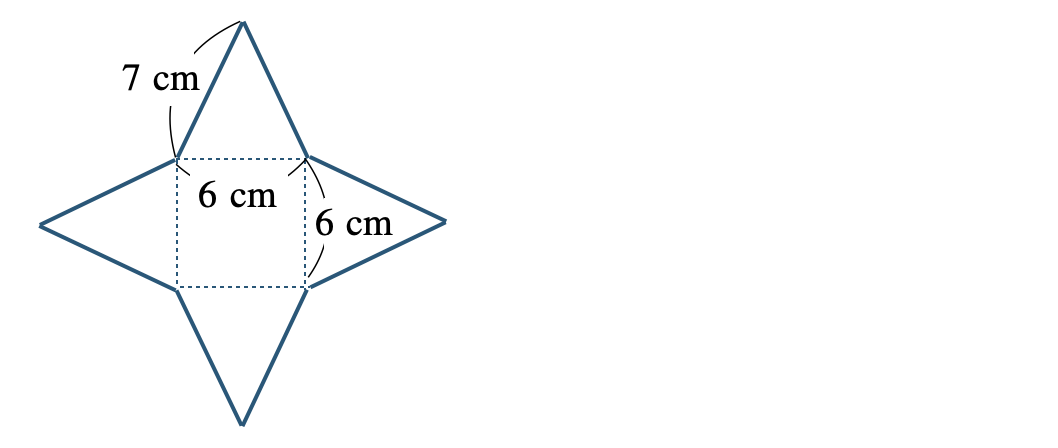
p.217 問3\(\begin{split}{\small (1)}~9~{\rm cm}^2\end{split}\) \(\begin{split}{\small (2)}~24~{\rm cm}^2\end{split}\)
\(\begin{split}{\small (3)}~33~{\rm cm}^2\end{split}\)
\(\begin{split}{\small (3)}~33~{\rm cm}^2\end{split}\)
■ 同じタイプの例題解説
» 立体の表面積
» 立体の表面積
p.217 問4おうぎ形の中心角の大きさは、
\(\begin{split}~~~\frac{\,6\pi \,}{\,16\pi \,}{\, \small \times \,} 360^\circ=135^\circ\end{split}\)
おうぎ形の面積は、
\(\begin{split}~~~8{\, \small \times \,} 8{\, \small \times \,} \pi {\, \small \times \,}\frac{\,135\,}{\,360\,}=24\pi\end{split}\)
底面積は、
\(\begin{split}~~~3{\, \small \times \,} 3{\, \small \times \,} \pi =9\pi\end{split}\)
よって、
\(\begin{split}~~~24\pi +9\pi =33\pi~{\rm cm}^2\end{split}\)
\(\begin{split}~~~\frac{\,6\pi \,}{\,16\pi \,}{\, \small \times \,} 360^\circ=135^\circ\end{split}\)
おうぎ形の面積は、
\(\begin{split}~~~8{\, \small \times \,} 8{\, \small \times \,} \pi {\, \small \times \,}\frac{\,135\,}{\,360\,}=24\pi\end{split}\)
底面積は、
\(\begin{split}~~~3{\, \small \times \,} 3{\, \small \times \,} \pi =9\pi\end{split}\)
よって、
\(\begin{split}~~~24\pi +9\pi =33\pi~{\rm cm}^2\end{split}\)
■ 同じタイプの例題解説
» 立体の表面積
» 立体の表面積
p.217 問5\(\begin{split}{\small (1)}~49\pi~{\rm cm}^2\end{split}\) \(\begin{split}{\small (2)}~84\pi~{\rm cm}^2\end{split}\)
\(\begin{split}{\small (3)}~133\pi~{\rm cm}^2\end{split}\)
\(\begin{split}{\small (3)}~133\pi~{\rm cm}^2\end{split}\)
■ 同じタイプの例題解説
» 立体の表面積
» 立体の表面積
5 球の体積と表面積
p.218 問1
\(\begin{split}{\small (1)}~\frac{\,4\,}{\,3\,}\pi~{\rm cm}^3\end{split}\) \(\begin{split}{\small (2)}~36\pi~{\rm cm}^3\end{split}\)
\(\begin{split}{\small (1)}~\frac{\,4\,}{\,3\,}\pi~{\rm cm}^3\end{split}\) \(\begin{split}{\small (2)}~36\pi~{\rm cm}^3\end{split}\)
■ 同じタイプの例題解説
» 球の体積と表面積
» 球の体積と表面積
p.219 問2\(\begin{split}{\small (1)}~16\pi~{\rm cm}^2\end{split}\) \(\begin{split}{\small (2)}~100\pi~{\rm cm}^2\end{split}\)
■ 同じタイプの例題解説
» 球の体積と表面積
» 球の体積と表面積
次のページ「7章 データの活用」