日本文教出版：中学数学１

p.200 問1立方体は、四角柱とも正四角柱ともいえる
直方体は四角柱といえるが、正四角柱とはいえない
※ 側面が合同とはならない

p.201 問2\({\small (1)}~\)六面体　　\({\small (2)}~\)五面体　　\({\small (3)}~\)四面体

p.201 問3　① 正八面体　　② 正十二面体
　③ 正二十面体

p.201 問4１つの頂点に集まる面の数が３つと４つがあり、同じにならない

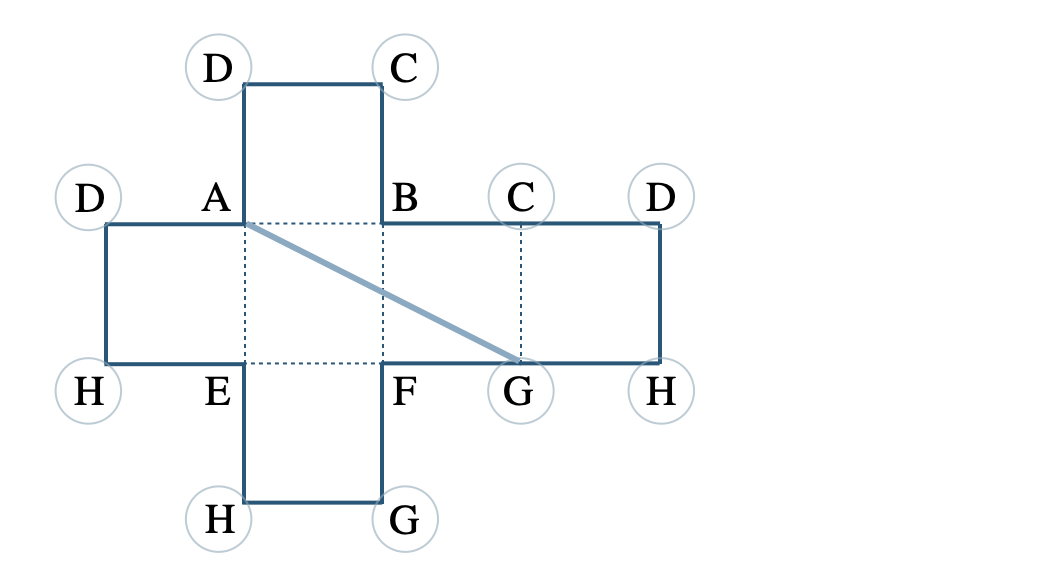
p.202 問1\({\small (1)}~\)辺 \({\rm DC~,~EF~,~HG}\)
\({\small (2)}~\)辺 \({\rm AD~,~AE~,~BC~,~BF}\)
\({\small (3)}~\)辺 \({\rm DH~,~EH~,~CG~,~FG}\)

p.203 問2　辺 \({\rm AE~,~AD}\)

p.203 問3　辺 \({\rm CH~,~DI~,~EJ~,~GH~,~HI~,~IJ~,~FJ}\)

p.205 問1\({\small (1)}~\)面 \({\rm ABC~,~ADFC}\)
\({\small (2)}~\)面 \({\rm DEF}\)
\({\small (3)}~\)辺 \({\rm AD~,~BE~,~CF}\)

p.205 問2　交わる

p.206 問3\({\small (1)}~\)面 \({\rm DHGC}\)
\({\small (2)}~\)面 \({\rm ABCD~,~BFGC~,~AEHD~,~EFGH}\)

p.206 問4\({\small (1)}~\)辺 \({\rm AD}\)　　\({\small (2)}~\)辺 \({\rm BD}\)

p.207 問1底面が半径 \(3~{\rm cm}\) の円で、高さが \(5~{\rm cm}\) の円柱

p.208 問2\({\small (1)}~\)円柱　　\({\small (2)}~\)球

p.209 問3　円柱は、長方形と円
　円錐は、二等辺三角形と円

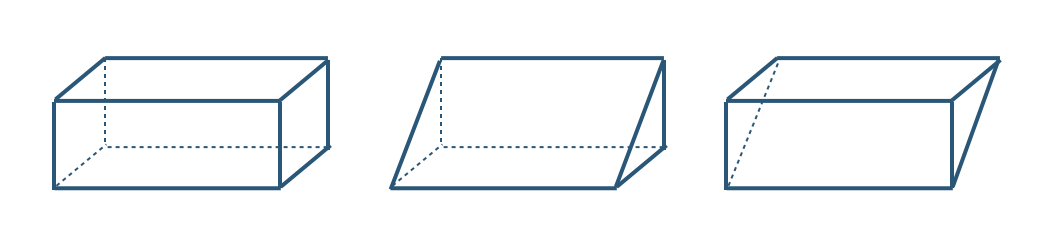
p.209 問4\({\small (1)}~\)底面の形、側面の数は同じ
　　側面の形、底面の数はちがう

---

\({\small (2)}~\)底面の形が円で同じ
　　底面の数がちがう

---

\({\small (3)}~\)底面の数が同じ
　　底面の形がちがう

p.210 問1

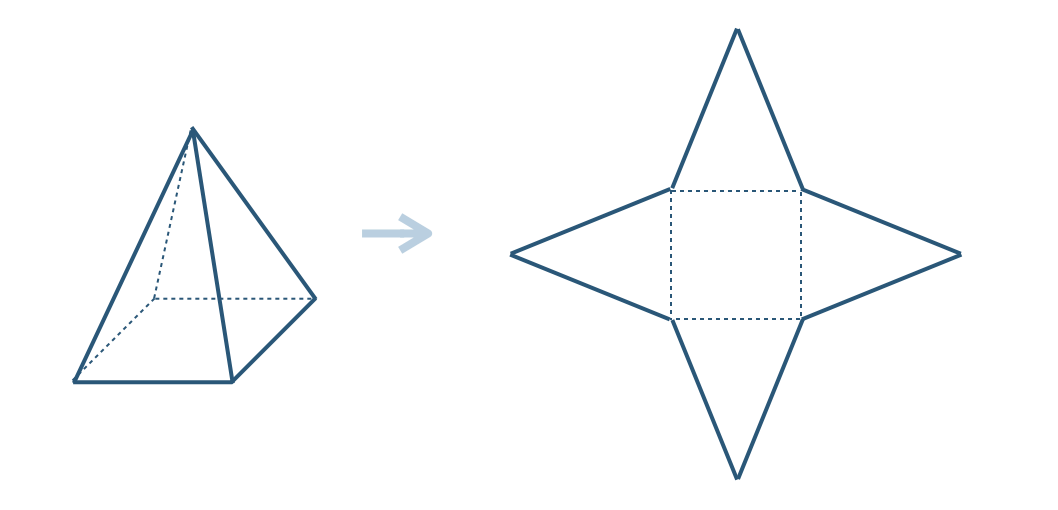
p.210 問2　辺 \({\rm EC}\)

p.211 問3\(\begin{split}{\small (1)}~16\pi~{\rm cm}\end{split}\)　　\(\begin{split}{\small (2)}~8~{\rm cm}\end{split}\)

p.211 問4\({\small (1)}~\)
\({\small (2)}~\)

p.212 問5\({\small (1)}~\)円柱　　\({\small (2)}~\)円錐　　\({\small (3)}~\)球

p.212 問6

p.213 基本の問題 1\({\small (1)}~\)辺 \({\rm EF}\)
\({\small (2)}~\)辺 \({\rm BC~,~EF}\)
\({\small (3)}~\)辺 \({\rm BE~,~CF}\)

p.213 基本の問題 2\({\small (1)}~\)エ　　\({\small (2)}~\)ア　　\({\small (3)}~\)イ　　\({\small (4)}~\)ウ

p.213 基本の問題 3\({\small (1)}~\)

\({\small (2)}~\)

p.214 問1　\(148~{\rm cm}^2\)

p.214 問2　\(105~{\rm cm}^2\)

p.215 問3　\(36\pi~{\rm cm}^2\)

p.215 問4\({\small (1)}~60\pi~{\rm cm}^2\)　　\({\small (2)}~20\pi~{\rm cm}^2\)

p.216 問1　\(200\pi~{\rm cm}^3\)

p.216 問2　\(35~{\rm cm}^2\)

p.217 問3

---

　円錐の体積は円柱の \(\begin{split}\frac{\,1\,}{\,3\,}\end{split}\) 倍

p.217 問4\({\small (1)}~96~{\rm cm}^3\)　　\({\small (2)}~80\pi~{\rm cm}^3\)

p.218 問1　\(100\pi~{\rm cm}^2\)

p.218 問2

---

　球の体積は円柱の \(\begin{split}\frac{\,2\,}{\,3\,}\end{split}\) 倍

p.219 問3　\(36\pi~{\rm cm}^3\)

p.219 問4　表面積 \(243\pi~{\rm cm}^2\)　　体積 \(486\pi~{\rm cm}^3\)

p.220 基本の問題 1\({\small (1)}~108~{\rm cm}^2\)　　\({\small (2)}~72~{\rm cm}^3\)

p.220 基本の問題 2\({\small (1)}~16\pi~{\rm cm}\)　　\({\small (2)}~8~{\rm cm}\)
\({\small (3)}~160\pi~{\rm cm}^2\)

p.220 基本の問題 3\({\small (1)}~30~{\rm cm}^3\)　　\({\small (2)}~108\pi~{\rm cm}^3\)

p.220 基本の問題 4\(\begin{split}{\small (1)}~400\pi~{\rm cm}^2\end{split}\)

---

\(\begin{split}{\small (2)}~\frac{\,4000\pi\,}{\,3\,}~{\rm cm}^3\end{split}\)、\(4000~{\rm cm}^3\) より大きい

---