啓林館：未来へ広がる数学１

p.217 問1\(~~~\)\(0.68\) 秒

p.218 問2\(~~~47~,~50\)

p.218 問3　(ア) \(46\) 回　　(イ) \(14\) 回

p.221 問4

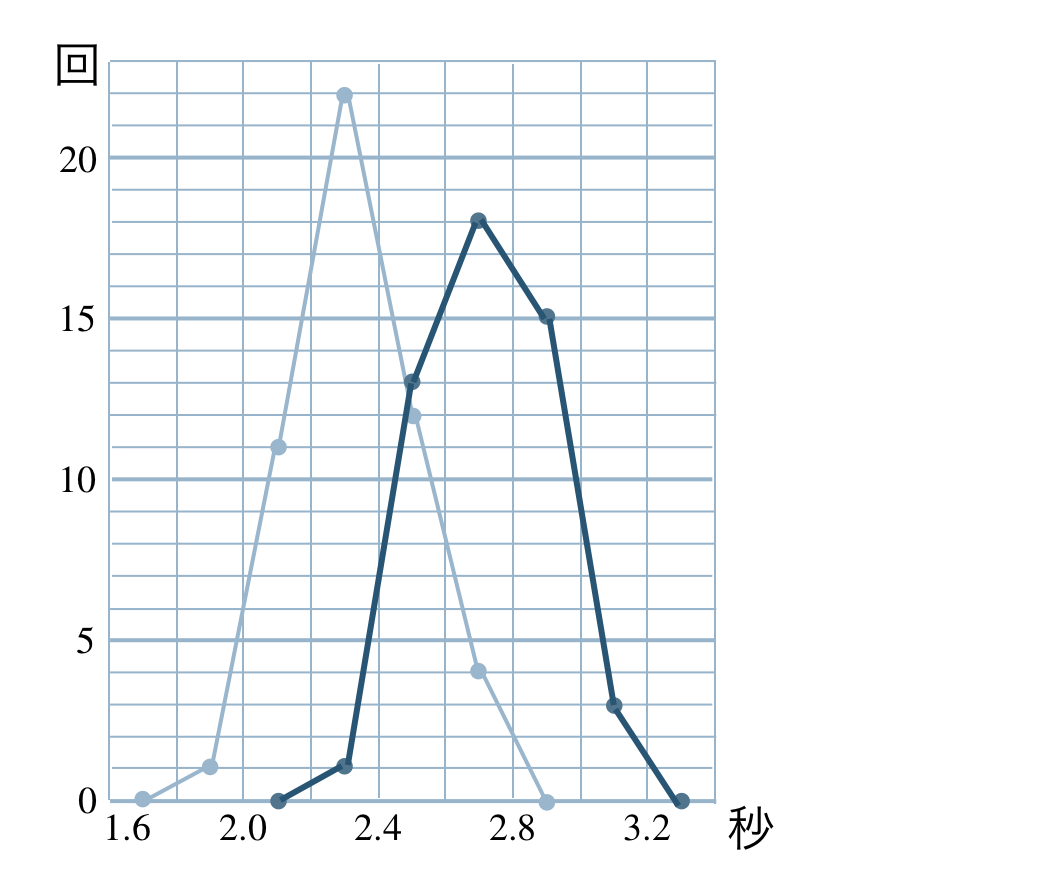
p.222 問5\(~~~1.90~,~2.10~,~2.30~,~2.50\)
\(~~~2.70~,~(2.90)~,~3.10\)

---

　(ア) の最頻値 \(2.30\) (秒)
　(イ) の最頻値 \(2.70\) (秒)

p.225 問6\(~~~0.03\)

p.226 問7相対度数
\(~~~0.03~,~0.03~,~(0.17)~,~(0.17)~,~0.30\)
\(~~~~,~0.10~,~0.10~,~0.03~,~0.07~,~1.00\)

---

累積相対度数
\(~~~0.03~,~0.06~,~0.23~,~0.40~,~0.70\)
\(~~~~,~0.80~,~0.90~,~0.93~,~1.00\)

p.226 問8　(イ) \(94~\)%　　(ウ) \(23~\)%

p.226 問9

p.231 問1階級値
\(~~~5~,~15~,~25~,~(35)~,~45~,~55\)

---

階級値×度数
\(~~~25~,~135~,~275~,~(105)~,~90~,~55~,~685\)

---

平均値は、約 \(22.1\) (分)
最頻値は \(25\) (分)
中央値が含まれる階級は \(20\) 分以上 \(30\) 分未満

p.235 問1　(イ) \(0.45\)　　(ウ) \(0.05\)　　(エ) \(0.03\)

p.235 問2　(イ)

p.236 問3\(~~~0.51\)

p.236 問4\(~~~0.75\)

p.237 問5\({\small (1)}~25\) 以上 \(30\) 分未満
\({\small (2)}~35\) 以上 \(40\) 分未満
\({\small (3)}~0.76\)