このページは「中学数学２ 式の計算」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう！
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
【問題一覧】中学数学２ 式の計算
多項式の項と次数
問題
\({\small (1)}~\)次の多項式の項を答えよ。
① \(3a-7b\)
② \(2x^2-5x+3\)
\({\small (2)}~\)次の単項式の次数を求めよ。
① \(3a^2\) ② \(-4x^2y\) ③ \(5x^2yz^3\)
\({\small (3)}~\)次の多項式の次数を答えよ。また、何次式か答えよ。
① \(2a+9b-5\)
② \(x^2-6x+5\)
③ \(3x^2y-10xy^3\)
次の問いに答えよ。
\({\small (1)}~\)次の多項式の項を答えよ。
① \(3a-7b\)
② \(2x^2-5x+3\)
\({\small (2)}~\)次の単項式の次数を求めよ。
① \(3a^2\) ② \(-4x^2y\) ③ \(5x^2yz^3\)
\({\small (3)}~\)次の多項式の次数を答えよ。また、何次式か答えよ。
① \(2a+9b-5\)
② \(x^2-6x+5\)
③ \(3x^2y-10xy^3\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(3a~,~-7b\)
② \(2x^2~,~-5x~,~3\)
\({\small (2)}~\)
① 次数 \(2\) ② 次数 \(3\) ③ 次数 \(6\)
\({\small (3)}~\)
① 次数 \(1\)、\(1\)次式
② 次数 \(2\)、\(2\)次式
③ 次数 \(4\)、\(4\)次式
多項式の項と次数
今回の問題は「多項式の項と次数」です。 \(~\)数研出版 これからの数学２ p.17~18 問1~...
jhs.yorikuwa.com
同類項と多項式の加法・減法
問題
\({\small (1)}~7a-3b+4a+10b\)
\({\small (2)}~8x^2-9x-5x^2+x-2\)
\({\small (3)}~(4x+7y)+(x-3y)\)
\({\small (4)}~(4x+7y)-(x-3y)\)
\({\small (5)}~~~\begin{array}{rr}
& 3a^2+a-2\\
+\big{)}&a^2-5a+6\\
\hline
\end{array}\)
\({\small (6)}~~~\begin{array}{rr}
& 3a^2+a-2\\
-\big{)}&a^2-5a+6\\
\hline
\end{array}\)
\({\small (7)}~\)２つの式 \(a+5b~,~7a-2b\) について、
① ２つの式の和を求めよ。
② 左の式から右の式を引いた差を求めよ。
次の計算や問いに答えよ。
\({\small (1)}~7a-3b+4a+10b\)
\({\small (2)}~8x^2-9x-5x^2+x-2\)
\({\small (3)}~(4x+7y)+(x-3y)\)
\({\small (4)}~(4x+7y)-(x-3y)\)
\({\small (5)}~~~\begin{array}{rr}
& 3a^2+a-2\\
+\big{)}&a^2-5a+6\\
\hline
\end{array}\)
\({\small (6)}~~~\begin{array}{rr}
& 3a^2+a-2\\
-\big{)}&a^2-5a+6\\
\hline
\end{array}\)
\({\small (7)}~\)２つの式 \(a+5b~,~7a-2b\) について、
① ２つの式の和を求めよ。
② 左の式から右の式を引いた差を求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~11a+7b\) \({\small (2)}~3x^2-8x-2\)
\({\small (3)}~5x+4y\) \({\small (4)}~3x+10y\)
\({\small (5)}~4a^2-4a+4\) \({\small (6)}~2a^2+6a-8\)
\({\small (7)}~\)
① \(8a+3b\) ② \(-6a+7b\)
同類項と多項式の加法・減法
今回の問題は「同類項と多項式の加法・減法」です。 \(~\)数研出版 これからの数学２ p.19~2...
jhs.yorikuwa.com
多項式と数の乗法・除法
問題
\(\begin{split}{\small (1)}~2(a-3b)\end{split}\)
\(\begin{split}{\small (2)}~\frac{\,1\,}{\,2\,}(10x-6y+8)\end{split}\)
\(\begin{split}{\small (3)}~(21a-15b){\, \small \div \,} 3\end{split}\)
\(\begin{split}{\small (4)}~(10x^2-35x-5){\, \small \div \,}\frac{\,5\,}{\,2\,}\end{split}\)
次の計算をせよ。
\(\begin{split}{\small (1)}~2(a-3b)\end{split}\)
\(\begin{split}{\small (2)}~\frac{\,1\,}{\,2\,}(10x-6y+8)\end{split}\)
\(\begin{split}{\small (3)}~(21a-15b){\, \small \div \,} 3\end{split}\)
\(\begin{split}{\small (4)}~(10x^2-35x-5){\, \small \div \,}\frac{\,5\,}{\,2\,}\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~2a-6b\) \({\small (2)}~5x-3y+4\)
\({\small (3)}~7a-5b\) \({\small (4)}~4x^2-14x-2\)
多項式と数の乗法・除法
今回の問題は「多項式と数の乗法・除法」です。 \(~\)数研出版 これからの数学２ p.21~22 ...
jhs.yorikuwa.com
いろいろな多項式と数の計算
問題
\(\begin{split}{\small (1)}~3(a-3b)+2(5a+6b)\end{split}\)
\(\begin{split}{\small (2)}~3(a-3b)-2(5a+6b)\end{split}\)
\(\begin{split}{\small (3)}~4(x^2-2x+1)+3(x-5)\end{split}\)
\(\begin{split}{\small (4)}~4(x^2-2x+1)-3(x-5)\end{split}\)
次の計算をせよ。
\(\begin{split}{\small (1)}~3(a-3b)+2(5a+6b)\end{split}\)
\(\begin{split}{\small (2)}~3(a-3b)-2(5a+6b)\end{split}\)
\(\begin{split}{\small (3)}~4(x^2-2x+1)+3(x-5)\end{split}\)
\(\begin{split}{\small (4)}~4(x^2-2x+1)-3(x-5)\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~13a+3b\) \({\small (2)}~-7a-21b\)
\({\small (3)}~4x^2-5x-11\) \({\small (4)}~4x^2-11x+19\)
いろいろな多項式と数の計算
今回の問題は「いろいろな多項式と数の計算」です。 \(~\)数研出版 これからの数学２ p.22 問...
jhs.yorikuwa.com
分数をふくむ多項式の計算
問題
\(\begin{split}&{\small (1)}~\frac{\,x+y\,}{\,2\,}+\frac{\,3x-2y\,}{\,4\,}\end{split}\)
\(\begin{split}&{\small (2)}~\frac{\,2a-b\,}{\,3\,}-\frac{\,a-5b\,}{\,2\,}\end{split}\)
\(\begin{split}&{\small (3)}~\frac{\,3a+2b\,}{\,10\,}-\frac{\,7a-3b\,}{\,15\,}\end{split}\)
\(\begin{split}&{\small (4)}~x+2y-\frac{\,x-2y\,}{\,5\,}\end{split}\)
次の計算をせよ。
\(\begin{split}&{\small (1)}~\frac{\,x+y\,}{\,2\,}+\frac{\,3x-2y\,}{\,4\,}\end{split}\)
\(\begin{split}&{\small (2)}~\frac{\,2a-b\,}{\,3\,}-\frac{\,a-5b\,}{\,2\,}\end{split}\)
\(\begin{split}&{\small (3)}~\frac{\,3a+2b\,}{\,10\,}-\frac{\,7a-3b\,}{\,15\,}\end{split}\)
\(\begin{split}&{\small (4)}~x+2y-\frac{\,x-2y\,}{\,5\,}\end{split}\)
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~\frac{\,5x\,}{\,4\,}\end{split}\) \(\begin{split}{\small (2)}~\frac{\,a+13b\,}{\,6\,}\end{split}\)
\(\begin{split}{\small (3)}~\frac{\,-5a+12b\,}{\,30\,}\end{split}\) \(\begin{split}{\small (4)}~\frac{\,4x+12y\,}{\,5\,}\end{split}\)
分数をふくむ多項式の計算
今回の問題は「分数をふくむ多項式の計算」です。 \(~\)数研出版 これからの数学２ p.23 問6...
jhs.yorikuwa.com
単項式の乗法
問題
\(\begin{split}{\small (1)}~5x{\, \small \times \,} 3y\end{split}\)
\(\begin{split}{\small (2)}~(-3xy){\, \small \times \,}(-5z)\end{split}\)
\(\begin{split}{\small (3)}~2a{\, \small \times \,} (-7a)\end{split}\)
\(\begin{split}{\small (4)}~(-xy){\, \small \times \,}\frac{\,2\,}{\,3\,}x^2y\end{split}\)
\(\begin{split}{\small (5)}~(-2a)^2\end{split}\)
\(\begin{split}{\small (6)}~\frac{\,1\,}{\,6\,}a{\, \small \times \,}(-3a)^2\end{split}\)
次の計算をせよ。
\(\begin{split}{\small (1)}~5x{\, \small \times \,} 3y\end{split}\)
\(\begin{split}{\small (2)}~(-3xy){\, \small \times \,}(-5z)\end{split}\)
\(\begin{split}{\small (3)}~2a{\, \small \times \,} (-7a)\end{split}\)
\(\begin{split}{\small (4)}~(-xy){\, \small \times \,}\frac{\,2\,}{\,3\,}x^2y\end{split}\)
\(\begin{split}{\small (5)}~(-2a)^2\end{split}\)
\(\begin{split}{\small (6)}~\frac{\,1\,}{\,6\,}a{\, \small \times \,}(-3a)^2\end{split}\)
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~15xy\end{split}\) \(\begin{split}{\small (2)}~15xyz\end{split}\)
\(\begin{split}{\small (3)}~-14a^2\end{split}\) \(\begin{split}{\small (4)}~-\frac{\,2\,}{\,3\,}x^3y^2\end{split}\)
\(\begin{split}{\small (5)}~4a^2\end{split}\) \(\begin{split}{\small (6)}~\frac{\,3\,}{\,2\,}a^3\end{split}\)
単項式の乗法
今回の問題は「単項式の乗法」です。 \(~\)数研出版 これからの数学２ p.24~25 問1~2 ...
jhs.yorikuwa.com
単項式の除法
問題
\(\begin{split}{\small (1)}~6x^2 {\, \small \div \,} 3x\end{split}\)
\(\begin{split}{\small (2)}~(-28ab){\, \small \div \,} 7b\end{split}\)
\(\begin{split}{\small (3)}~20x^3y {\, \small \div \,}(-5xy)\end{split}\)
\(\begin{split}{\small (4)}~(-8ab^2){\, \small \div \,}\frac{\,b\,}{\,4\,}\end{split}\)
\(\begin{split}{\small (5)}~\left(-\frac{\,1\,}{\,7\,}a^3\right) {\, \small \div \,} \left(-\frac{\,1\,}{\,14\,}a\right)\end{split}\)
\(\begin{split}{\small (6)}~\frac{\,3\,}{\,10\,}x^3y^2{\, \small \div \,}\left(-\frac{\,6\,}{\,5\,}xy\right)\end{split}\)
次の計算をせよ。
\(\begin{split}{\small (1)}~6x^2 {\, \small \div \,} 3x\end{split}\)
\(\begin{split}{\small (2)}~(-28ab){\, \small \div \,} 7b\end{split}\)
\(\begin{split}{\small (3)}~20x^3y {\, \small \div \,}(-5xy)\end{split}\)
\(\begin{split}{\small (4)}~(-8ab^2){\, \small \div \,}\frac{\,b\,}{\,4\,}\end{split}\)
\(\begin{split}{\small (5)}~\left(-\frac{\,1\,}{\,7\,}a^3\right) {\, \small \div \,} \left(-\frac{\,1\,}{\,14\,}a\right)\end{split}\)
\(\begin{split}{\small (6)}~\frac{\,3\,}{\,10\,}x^3y^2{\, \small \div \,}\left(-\frac{\,6\,}{\,5\,}xy\right)\end{split}\)
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~2x\end{split}\) \(\begin{split}{\small (2)}~-4a\end{split}\)
\(\begin{split}{\small (3)}~-4x^2\end{split}\) \(\begin{split}{\small (4)}~-32ab\end{split}\)
\(\begin{split}{\small (5)}~2a^2\end{split}\) \(\begin{split}{\small (6)}~-\frac{\,x^2y\,}{\,4\,}\end{split}\)
単項式の除法
今回の問題は「単項式の除法」です。 \(~\)数研出版 これからの数学２ p.25~26 問3~5 ...
jhs.yorikuwa.com
３つの単項式の乗法・除法
問題
\(\begin{split}{\small (1)}~\left(-4a^2\right){\, \small \times \,} 3b {\, \small \div \,} 24ab\end{split}\)
\(\begin{split}{\small (2)}~(-5x){\, \small \div \,} (-15x){\, \small \times \,} (-6x)\end{split}\)
\(\begin{split}{\small (3)}~18a^2b {\, \small \div \,}(-3b){\, \small \div \,}(-6a)\end{split}\)
\(\begin{split}{\small (4)}~20x^3y^2 {\, \small \div \,} \frac{\,6\,}{\,7\,}xy {\, \small \div \,} \frac{\,5\,}{\,9\,}x^2\end{split}\)
次の計算をせよ。
\(\begin{split}{\small (1)}~\left(-4a^2\right){\, \small \times \,} 3b {\, \small \div \,} 24ab\end{split}\)
\(\begin{split}{\small (2)}~(-5x){\, \small \div \,} (-15x){\, \small \times \,} (-6x)\end{split}\)
\(\begin{split}{\small (3)}~18a^2b {\, \small \div \,}(-3b){\, \small \div \,}(-6a)\end{split}\)
\(\begin{split}{\small (4)}~20x^3y^2 {\, \small \div \,} \frac{\,6\,}{\,7\,}xy {\, \small \div \,} \frac{\,5\,}{\,9\,}x^2\end{split}\)
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~-\frac{\,a\,}{\,2\,}\end{split}\) \(\begin{split}{\small (2)}~-2x\end{split}\)
\(\begin{split}{\small (3)}~a\end{split}\) \(\begin{split}{\small (4)}~42y\end{split}\)
３つの単項式の乗法・除法
今回の問題は「３つの単項式の乗法・除法」です。 \(~\)数研出版 これからの数学２ p.27 問6...
jhs.yorikuwa.com
多項式と式の値
問題
\(\begin{split}a=-3~,~b={\frac{\,1\,}{\,2\,}}\end{split}\) のとき、次の式の値を求めよ。
\(\begin{split}{\small (1)}~a+6b\end{split}\)
\(\begin{split}{\small (2)}~a^2-2ab\end{split}\)
\(\begin{split}{\small (3)}~20a^3b^2{\, \small \div \,}\left(-5a^2b\right)\end{split}\)
\(\begin{split}{\small (4)}~2(3a-5b)-3(3a-2b)\end{split}\)
\(\begin{split}a=-3~,~b={\frac{\,1\,}{\,2\,}}\end{split}\) のとき、次の式の値を求めよ。
\(\begin{split}{\small (1)}~a+6b\end{split}\)
\(\begin{split}{\small (2)}~a^2-2ab\end{split}\)
\(\begin{split}{\small (3)}~20a^3b^2{\, \small \div \,}\left(-5a^2b\right)\end{split}\)
\(\begin{split}{\small (4)}~2(3a-5b)-3(3a-2b)\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~0\) \({\small (2)}~12\)
\({\small (3)}~6\) \({\small (4)}~7\)
多項式と式の値
今回の問題は「多項式と式の値」です。 \(~\)数研出版 これからの数学２ p.28 問1~2 \(...
jhs.yorikuwa.com
文字式の利用と数の性質
問題
\({\small (1)}~\)偶数と奇数の和は奇数である
\({\small (2)}~\)連続する３つの整数の和は３の倍数である
\({\small (3)}~\)２けたの自然数と、その数の十の位の数と一の位の数を入れかえた数の和は１１の倍数である
次のことを文字を使って説明せよ。
\({\small (1)}~\)偶数と奇数の和は奇数である
\({\small (2)}~\)連続する３つの整数の和は３の倍数である
\({\small (3)}~\)２けたの自然数と、その数の十の位の数と一の位の数を入れかえた数の和は１１の倍数である
[ 解答を見る ]
【解答】
\({\small (1)}~\)\(m~,~n\) 整数として、
偶然を \(2m\)、奇数を \(2n+1\) とすると、
偶然と奇数の和は、
\(\begin{split}&2m+(2n+1)\\[2pt]~~=~&2m+2n+1\\[2pt]~~=~&2(m+n)+1\end{split}\)
ここで、\(m+n\) は整数であるから
\(2(m+n)+1\) は奇数である
したがって、偶数と奇数の和は奇数である
\({\small (2)}~\)\(n\) を整数として、
連続する３つの整数を \(n~,~n+1~,~n+2\)とすると、
連続する３つの整数の和は、
\(\begin{split}&n+(n+1)+(n+2)\\[2pt]~~=~&n+n+1+n+2\\[2pt]~~=~&n+n+n+1+2\\[2pt]~~=~&(1+1+1)n+(1+2)\\[2pt]~~=~&3n+3\\[2pt]~~=~&3(n+1)\end{split}\)
ここで、\(n+1\) は整数であるから
\(3(n+1)\) は３の倍数である
したがって、
連続する３つの整数の和は３の倍数である
\({\small (3)}~\)\(a~,~b\) を整数として、
もとの自然数の十の位の数を \(a\)、一の位の数を \(b\) とすると、もとの自然数は \(10a+b\) となる
また、十の位の数と一の位の数を入れかえた数は、十の位の数が \(b\)、一の位の数が \(a\) となるので \(10b+a\) となる
これより、この２つの数の和は、
\(\begin{split}&(10a+b)+(10b+a)\\[2pt]~~=~&10a+b+10b+a\\[2pt]~~=~&10a+a+b+10b\\[2pt]~~=~&(10+1)a+(1+10)b\\[2pt]~~=~&11a+11b\\[2pt]~~=~&11(a+b)\end{split}\)
ここで、\(a+b\) は整数であるから
\(11(a+b)\) は１１の倍数である
したがって、２けたの自然数と、その数の十の位の数と一の位の数を入れかえた数の和は１１の倍数である
文字式の利用と数の性質
今回の問題は「文字式の利用と数の性質」です。 \(~\)数研出版 これからの数学２ p.31~33 ...
jhs.yorikuwa.com
文字式の利用と図形の性質
問題
次の図のような、直線部分が \(a~({\rm m})\)、半円部分の半径が \(r~({\rm m})\) のトラックがある。このとき、トラック１周の長さを文字式で表せ。
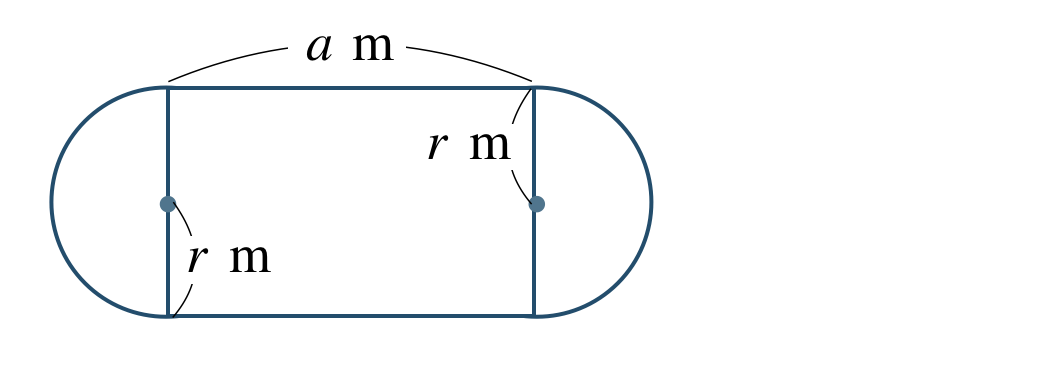
[ 解答を見る ]
【解答】
\(~~~2\pi r+2a~({\rm m})\)
文字式の利用と図形の性質
今回の問題は「文字式の利用と図形の性質」です。 \(~\)数研出版 これからの数学２ p.33~34...
jhs.yorikuwa.com
等式の変形
問題
\(\begin{split}{\small (1)}~y=2x-5~~[\,x\,]\end{split}\)
\(\begin{split}{\small (2)}~3x-7y=1~~[\,y\,]\end{split}\)
\(\begin{split}{\small (3)}~\frac{\,1\,}{\,2\,}ab=8~~[\,a\,]\end{split}\)
\(\begin{split}{\small (4)}~l=2\pi r~~[\,r\,]\end{split}\)
\(\begin{split}{\small (5)}~V=\frac{\,1\,}{\,3\,}Sh~~[\,S\,]\end{split}\)
\(\begin{split}{\small (6)}~V=\pi r^2 h~~[\,h\,]\end{split}\)
次の等式を [ ] の中の文字について解きなさい。
\(\begin{split}{\small (1)}~y=2x-5~~[\,x\,]\end{split}\)
\(\begin{split}{\small (2)}~3x-7y=1~~[\,y\,]\end{split}\)
\(\begin{split}{\small (3)}~\frac{\,1\,}{\,2\,}ab=8~~[\,a\,]\end{split}\)
\(\begin{split}{\small (4)}~l=2\pi r~~[\,r\,]\end{split}\)
\(\begin{split}{\small (5)}~V=\frac{\,1\,}{\,3\,}Sh~~[\,S\,]\end{split}\)
\(\begin{split}{\small (6)}~V=\pi r^2 h~~[\,h\,]\end{split}\)
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~x=\frac{\,y+5\,}{\,2\,}\end{split}\)
\(\begin{split}{\small (2)}~y=\frac{\,3x-1\,}{\,7\,}\end{split}\)
\(\begin{split}{\small (3)}~a=\frac{\,16\,}{\,b\,}\end{split}\)
\(\begin{split}{\small (4)}~r=\frac{\,l\,}{\,2\pi\,}\end{split}\)
\(\begin{split}{\small (5)}~S=\frac{\,3V\,}{\,h\,}\end{split}\)
\(\begin{split}{\small (6)}~h=\frac{\,V\,}{\,\pi r^2\,}\end{split}\)
等式の変形
今回の問題は「等式の変形」です。 \(~\)数研出版 これからの数学２ p.36 問2~3 \(~\...
jhs.yorikuwa.com
