このページは教科書改訂(令和7年度、2025年度)に対応済みの内容です。
このページは、啓林館:未来へ広がる数学1
5章 平面図形(令和7年度対応)
5章 平面図形(令和7年度対応)

教科書に完全対応の問題集|教科書ぴったりトレーニング
教科書に対応した数学の問題集|教科書ぴったりトレーニングの紹介 こんにちは、みなさん!今回は中学生の...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
啓林館中1 1章 正の数・負の数(令和7年度対応)
啓林館中1 2章 文字の式(令和7年度対応)
啓林館中1 3章 方程式(令和7年度対応)
啓林館中1 4章 変化と対応(令和7年度対応)
啓林館中1 5章 平面図形(令和7年度対応)
啓林館中1 6章 空間図形(令和7年度対応)
啓林館中1 7章 データの活用
5章 平面図形
1 直線と図形
1 直線と図形
p.151 問2\(\begin{split}{\small (1)}~\angle {\rm DCA}=65^\circ\end{split}\) \(\begin{split}{\small (2)}~\angle {\rm POS}=130^\circ\end{split}\)
■ 同じタイプの例題解説
» 平面上の図形の表し方
» 平面上の図形の表し方
p.152 問3\(\begin{split}~~~{\rm AC}\perp{\rm BD}\end{split}\)
■ 同じタイプの例題解説
» 平面上の図形の表し方
» 平面上の図形の表し方
p.153 説明しよう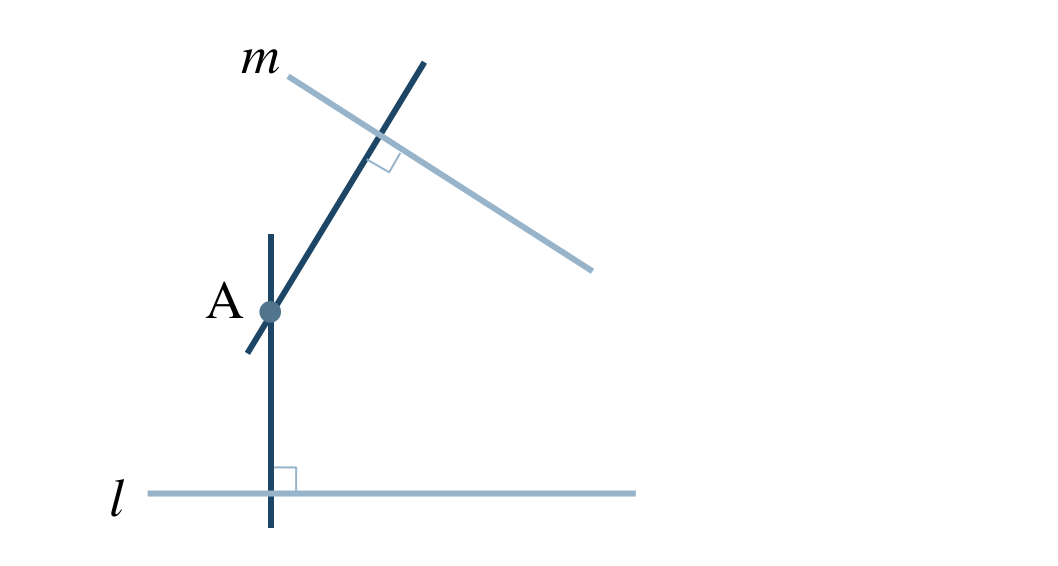
点 \({\rm A}\) と直線 \(l\) :\(1.5~{\rm cm}\)
点 \({\rm A}\) と直線 \(m\) :\(2~{\rm cm}\)
① 直線 \(l~(m)\) にそって三角定規を1つ付ける
② もう1つの三角定規の直角の部分をこの直線 \(l~(m)\) に付けてスライドさせる
③ 点Aに合わせて、点Aから直線 \(l~(m)\) に線を引く

点 \({\rm A}\) と直線 \(l\) :\(1.5~{\rm cm}\)
点 \({\rm A}\) と直線 \(m\) :\(2~{\rm cm}\)
① 直線 \(l~(m)\) にそって三角定規を1つ付ける
② もう1つの三角定規の直角の部分をこの直線 \(l~(m)\) に付けてスライドさせる
③ 点Aに合わせて、点Aから直線 \(l~(m)\) に線を引く
■ 同じタイプの例題解説
» 平面上の図形の表し方
» 平面上の図形の表し方
p.153 問4\(\begin{split}~~~{\rm AD} \,//\, {\rm BC}\end{split}\)
■ 同じタイプの例題解説
» 平面上の図形の表し方
» 平面上の図形の表し方
p.153 問5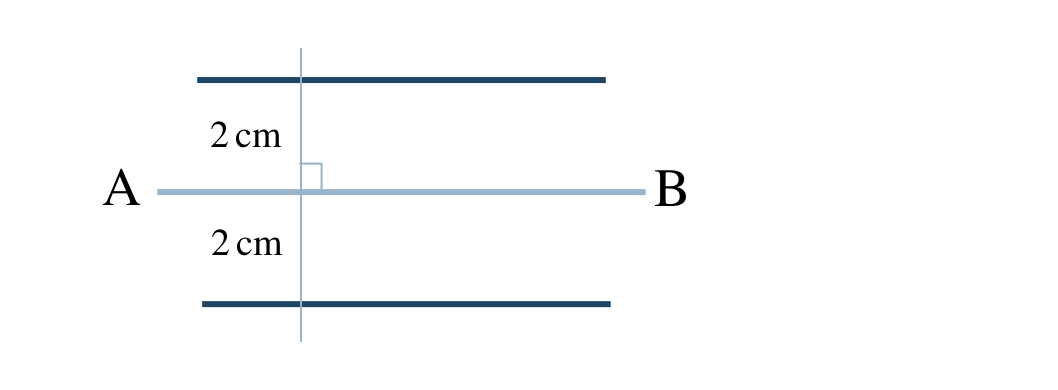
\(~~~2\) 本
① 問4と同じ方法で直線ABに垂直な線を引く
② この垂直な線にそって三角定規を付ける
このとき、目盛りを合わせておく
③ もう1つの三角定規の直角部分を付けて \(2~{\rm cm}\) 離れたところまでスライドさせて平行な線を引く
(上側と下側の2本引ける)
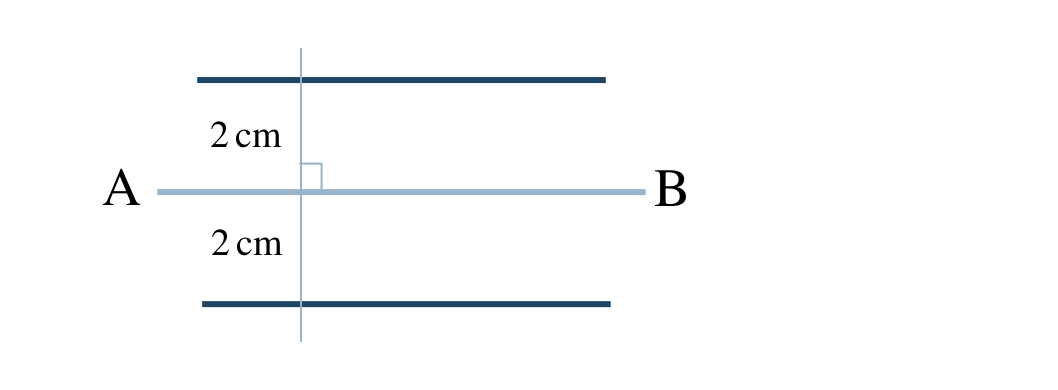
\(~~~2\) 本
① 問4と同じ方法で直線ABに垂直な線を引く
② この垂直な線にそって三角定規を付ける
このとき、目盛りを合わせておく
③ もう1つの三角定規の直角部分を付けて \(2~{\rm cm}\) 離れたところまでスライドさせて平行な線を引く
(上側と下側の2本引ける)
■ 同じタイプの例題解説
» 平面上の図形の表し方
» 平面上の図形の表し方
p.154 問6\(\begin{split}~~~\triangle {\rm ABC}~,~\triangle {\rm ABD}~,~\triangle {\rm ADC}\end{split}\)
■ 同じタイプの例題解説
» 平面上の図形の表し方
» 平面上の図形の表し方
p.154 問7\({\small (1)}~\)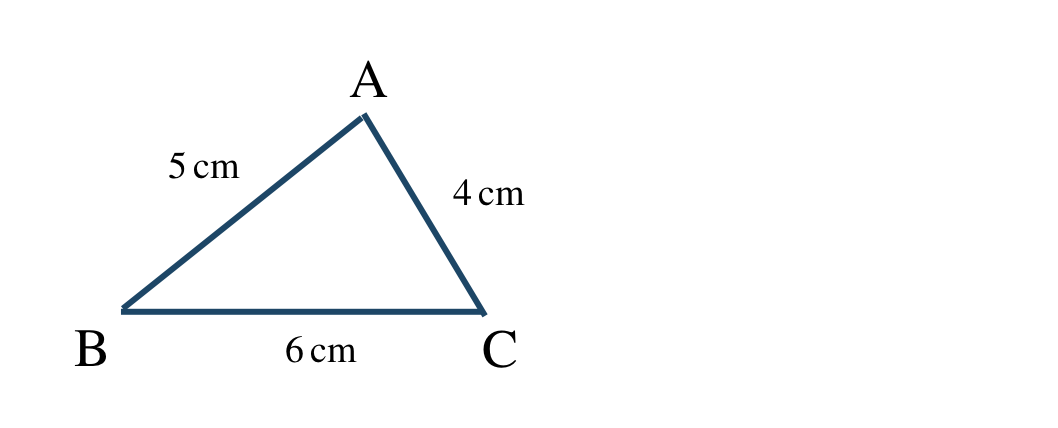
① \(6~{\rm cm}\) の辺BCを引く
② コンパスで \(5~{\rm cm}\) をはかり、点Bから円を描く
③ コンパスで \(4~{\rm cm}\) をはかり、点Cから円を描く
④ 2つの円の交点が点Aで、点B、Cと結ぶ
\({\small (2)}~\)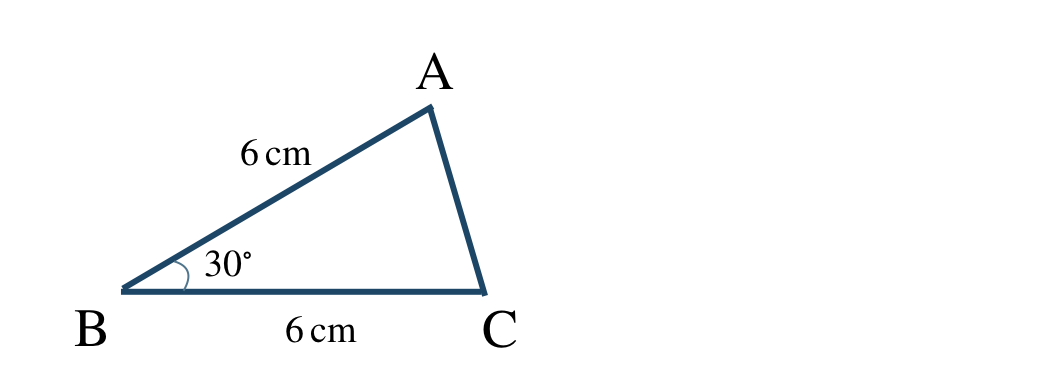
① \(6~{\rm cm}\) の辺BCを引く
② 分度器で点Bから \(30^\circ\) をはかり、線を引く
③ 点Bから \(6~{\rm cm}\) のところが点Aとなる
④ 点Aと点Cを結ぶ
\({\small (3)}~\)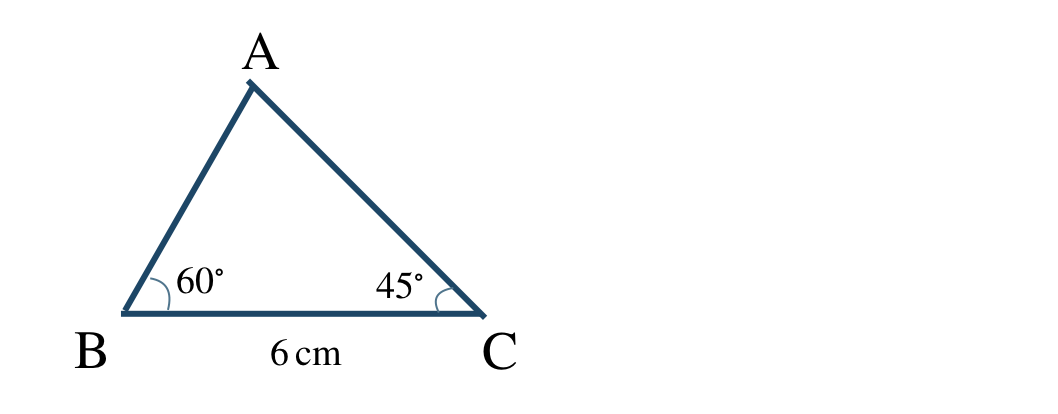
① \(6~{\rm cm}\) の辺BCを引く
② 分度器で点Bから \(60^\circ\) をはかり、線を引く
③ 分度器で点Cから \(45^\circ\) をはかり、線を引く
④ 2つの線の交点が点Aとなる
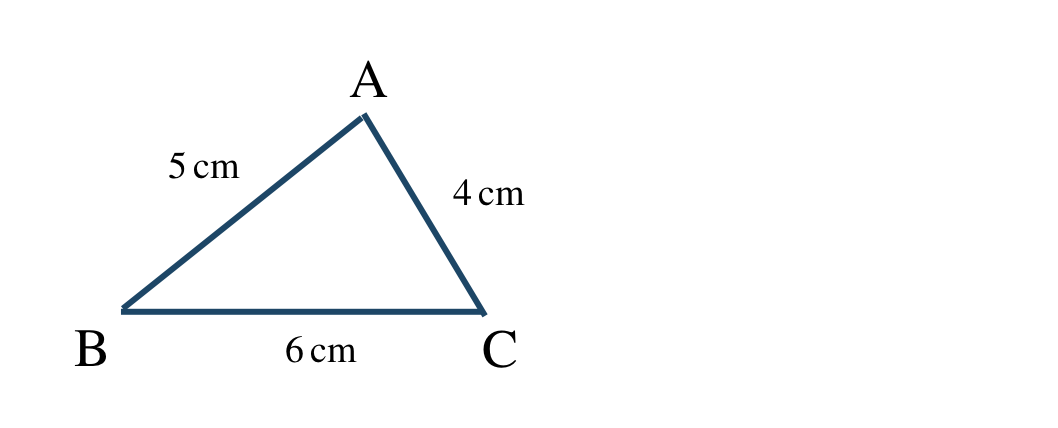
① \(6~{\rm cm}\) の辺BCを引く
② コンパスで \(5~{\rm cm}\) をはかり、点Bから円を描く
③ コンパスで \(4~{\rm cm}\) をはかり、点Cから円を描く
④ 2つの円の交点が点Aで、点B、Cと結ぶ
\({\small (2)}~\)

① \(6~{\rm cm}\) の辺BCを引く
② 分度器で点Bから \(30^\circ\) をはかり、線を引く
③ 点Bから \(6~{\rm cm}\) のところが点Aとなる
④ 点Aと点Cを結ぶ
\({\small (3)}~\)

① \(6~{\rm cm}\) の辺BCを引く
② 分度器で点Bから \(60^\circ\) をはかり、線を引く
③ 分度器で点Cから \(45^\circ\) をはかり、線を引く
④ 2つの線の交点が点Aとなる
p.154 問8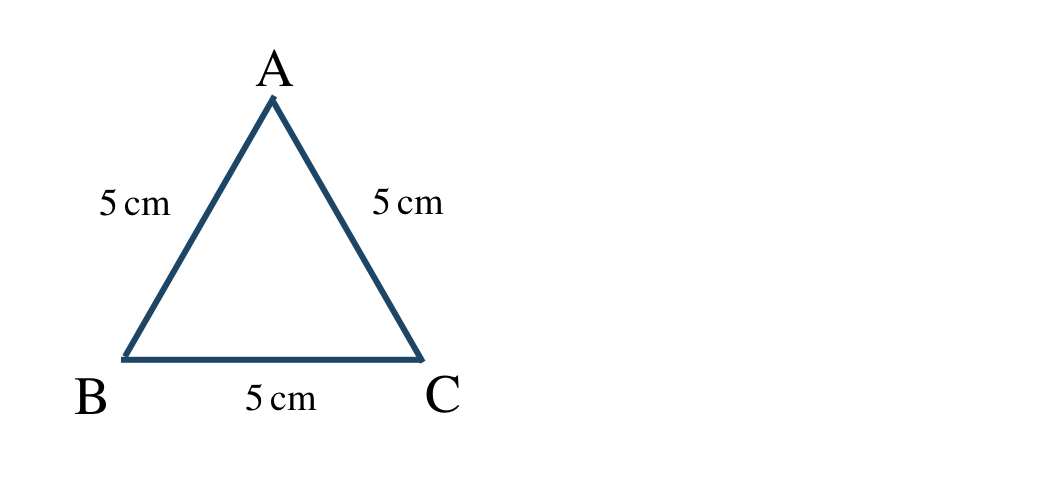
① \(5~{\rm cm}\) の辺BCを引く
② コンパスで \(5~{\rm cm}\) をはかり、点Bと点Cをそれぞれ中心とした円を描く
③ 2つの円の交点が点Aとなり、点B、点Cと結ぶ
(点Aは上側と下側の2つできるので、どちらでもよい)
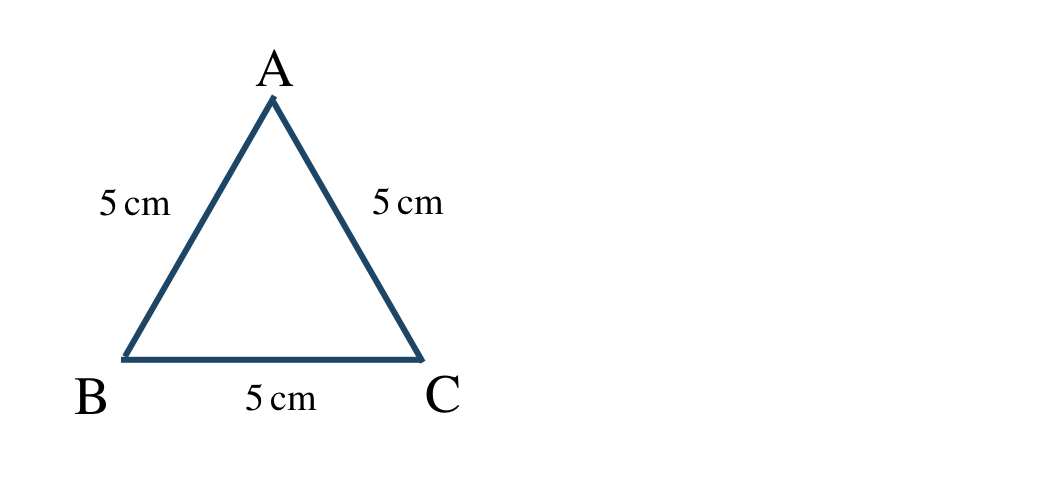
① \(5~{\rm cm}\) の辺BCを引く
② コンパスで \(5~{\rm cm}\) をはかり、点Bと点Cをそれぞれ中心とした円を描く
③ 2つの円の交点が点Aとなり、点B、点Cと結ぶ
(点Aは上側と下側の2つできるので、どちらでもよい)
2節 移動と作図
1 図形と移動
p.156 問1\(~~~\) 平行で長さが等しい
■ 同じタイプの例題解説
» 図形の平行移動
» 図形の平行移動
p.157 問3
① 直線APを引く
② 三角定規を使い、点Bから直線APに平行な直線を引く
点Cからも同じように引く
③ コンパスで線分APの長さをはかり、点B、Cから同じ長さの点をそれぞれの直線上にとる
④ 点Pとこの2つの点を結ぶ

① 直線APを引く
② 三角定規を使い、点Bから直線APに平行な直線を引く
点Cからも同じように引く
③ コンパスで線分APの長さをはかり、点B、Cから同じ長さの点をそれぞれの直線上にとる
④ 点Pとこの2つの点を結ぶ
■ 同じタイプの例題解説
» 図形の平行移動
» 図形の平行移動
p.157 問4 線分 \({\rm OA}\)、\({\rm OP}\) は長さが等しい
■ 同じタイプの例題解説
» 図形の回転移動
» 図形の回転移動
p.158 問5
① 3点A、B、Cと点Oを結ぶ直線をそれぞれ引く
② OAの長さをコンパスではかり、点Oを中心として点Aとは逆方向でOAと同じ長さのところに点をとる
③ 点B、点Cでも同じように点をとる
④ 3点を結ぶ

① 3点A、B、Cと点Oを結ぶ直線をそれぞれ引く
② OAの長さをコンパスではかり、点Oを中心として点Aとは逆方向でOAと同じ長さのところに点をとる
③ 点B、点Cでも同じように点をとる
④ 3点を結ぶ
■ 同じタイプの例題解説
» 図形の回転移動
» 図形の回転移動
p.158 問6線分 \({\rm AP}\)、\({\rm BQ}\)、\({\rm CR}\) と対称の軸 \(l\) は垂直に交わり、その交点で2等分される
■ 同じタイプの例題解説
» 図形の対称移動
» 図形の対称移動
p.159 問7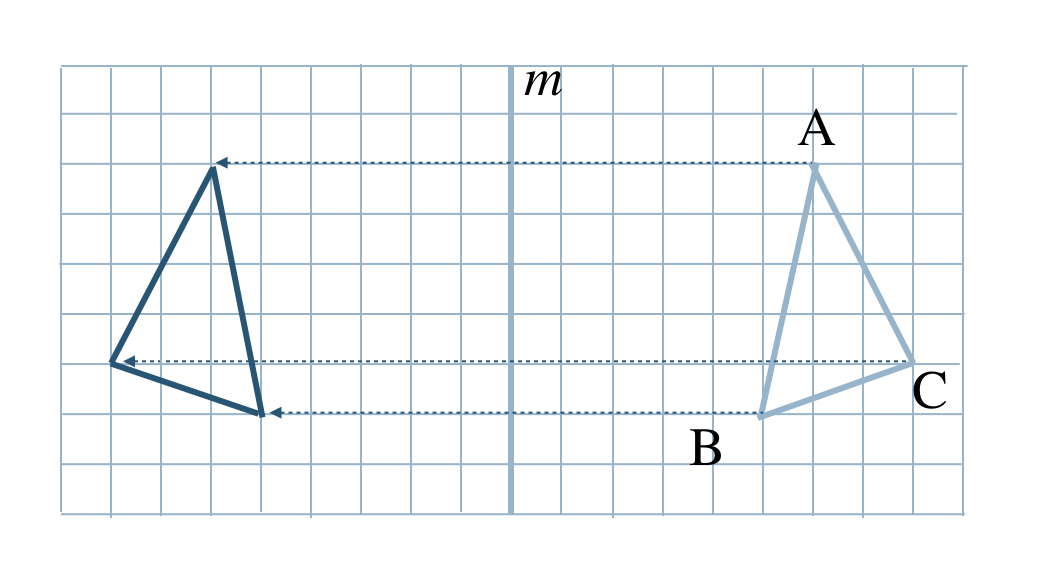
① 点Aは軸 \(m\) と6マス離れているので、点Aとは逆方向に6マス離れたところに点をとる
② 点Bは軸 \(m\) と5マス離れているので、点Bとは逆方向に5マス離れたところに点をとる
③ 点Cは軸 \(m\) と8マス離れているので、点Cとは逆方向に8マス離れたところに点をとる
④ 3点を結ぶ

① 点Aは軸 \(m\) と6マス離れているので、点Aとは逆方向に6マス離れたところに点をとる
② 点Bは軸 \(m\) と5マス離れているので、点Bとは逆方向に5マス離れたところに点をとる
③ 点Cは軸 \(m\) と8マス離れているので、点Cとは逆方向に8マス離れたところに点をとる
④ 3点を結ぶ
■ 同じタイプの例題解説
» 図形の対称移動
» 図形の対称移動
p.161 練習問題 1\(\begin{split}{\small (1)}~\triangle {\rm COQ}\end{split}\)
\(\begin{split}{\small (2)}~\triangle {\rm OBP}\end{split}\)
\(\begin{split}{\small (3)}~\triangle {\rm ODS}~,~\triangle {\rm OCR}~,~\triangle {\rm OBQ}\end{split}\)
\(\begin{split}{\small (4)}~\triangle {\rm OCQ}\end{split}\)
\(\begin{split}{\small (2)}~\triangle {\rm OBP}\end{split}\)
\(\begin{split}{\small (3)}~\triangle {\rm ODS}~,~\triangle {\rm OCR}~,~\triangle {\rm OBQ}\end{split}\)
\(\begin{split}{\small (4)}~\triangle {\rm OCQ}\end{split}\)
■ 同じタイプの例題解説
» 図形の移動のまとめ
» 図形の移動のまとめ
2 基本の作図
p.163 問1\({\small (1)}~\)
① 点B、Cを中心とした等しい半径の円をそれぞれ描く
② 2つの交点を結ぶ
\({\small (2)}~\)
① 点A、Bを中心とした等しい半径の円をそれぞれ描く
② 2つの交点を結ぶ

① 点B、Cを中心とした等しい半径の円をそれぞれ描く
② 2つの交点を結ぶ
\({\small (2)}~\)

① 点A、Bを中心とした等しい半径の円をそれぞれ描く
② 2つの交点を結ぶ
■ 同じタイプの例題解説
» 垂直二等分線の作図
» 垂直二等分線の作図
p.163 問2\({\small (1)}~\)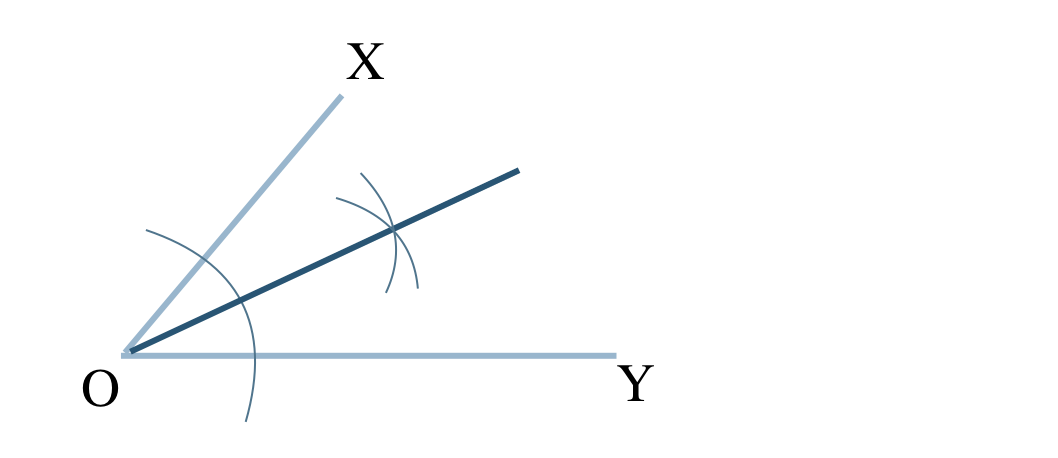
① 点Oを中心とした円を描く
② この円と半直線OX、OYとの交点を中心とした等しい半径の円をそれぞれ描き、交点をとる
③ 点Oとこの交点を結ぶ
\({\small (2)}~\)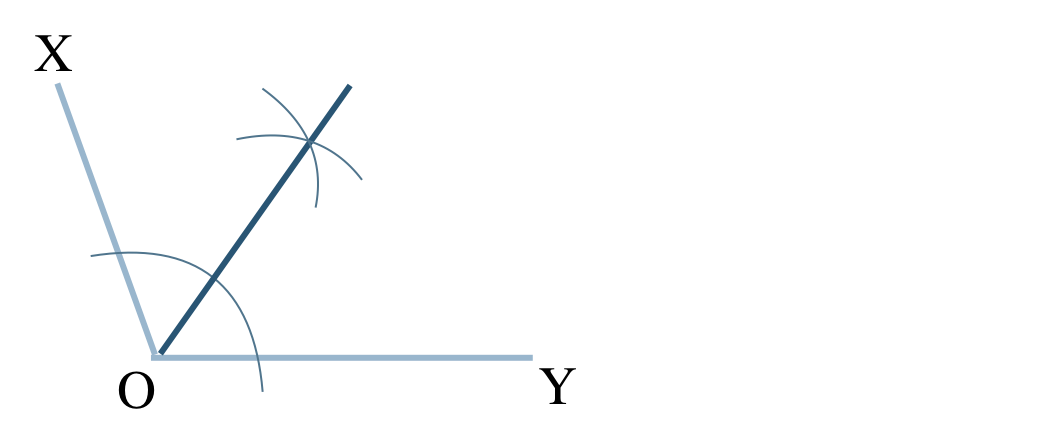
① 点Oを中心とした円を描く
② この円と半直線OX、OYとの交点を中心とした等しい半径の円をそれぞれ描き、この2つの円の交点をとる
③ 点Oとこの交点を結ぶ

① 点Oを中心とした円を描く
② この円と半直線OX、OYとの交点を中心とした等しい半径の円をそれぞれ描き、交点をとる
③ 点Oとこの交点を結ぶ
\({\small (2)}~\)
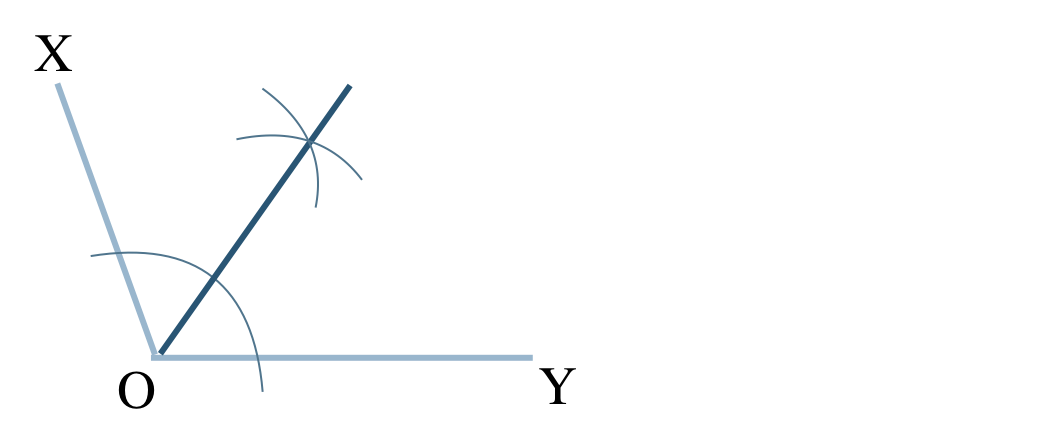
① 点Oを中心とした円を描く
② この円と半直線OX、OYとの交点を中心とした等しい半径の円をそれぞれ描き、この2つの円の交点をとる
③ 点Oとこの交点を結ぶ
■ 同じタイプの例題解説
» 角の二等分線の作図
» 角の二等分線の作図
p.164 問3
① 点Pを中心とする円を描く
② この円と辺BCとの交点を中心とした等しい半径の円をそれぞれ描き、この2つの円の交点をとる
③ 点Pとこの交点を結ぶ

① 点Pを中心とする円を描く
② この円と辺BCとの交点を中心とした等しい半径の円をそれぞれ描き、この2つの円の交点をとる
③ 点Pとこの交点を結ぶ
■ 同じタイプの例題解説
» 垂線の作図
» 垂線の作図
p.165 問4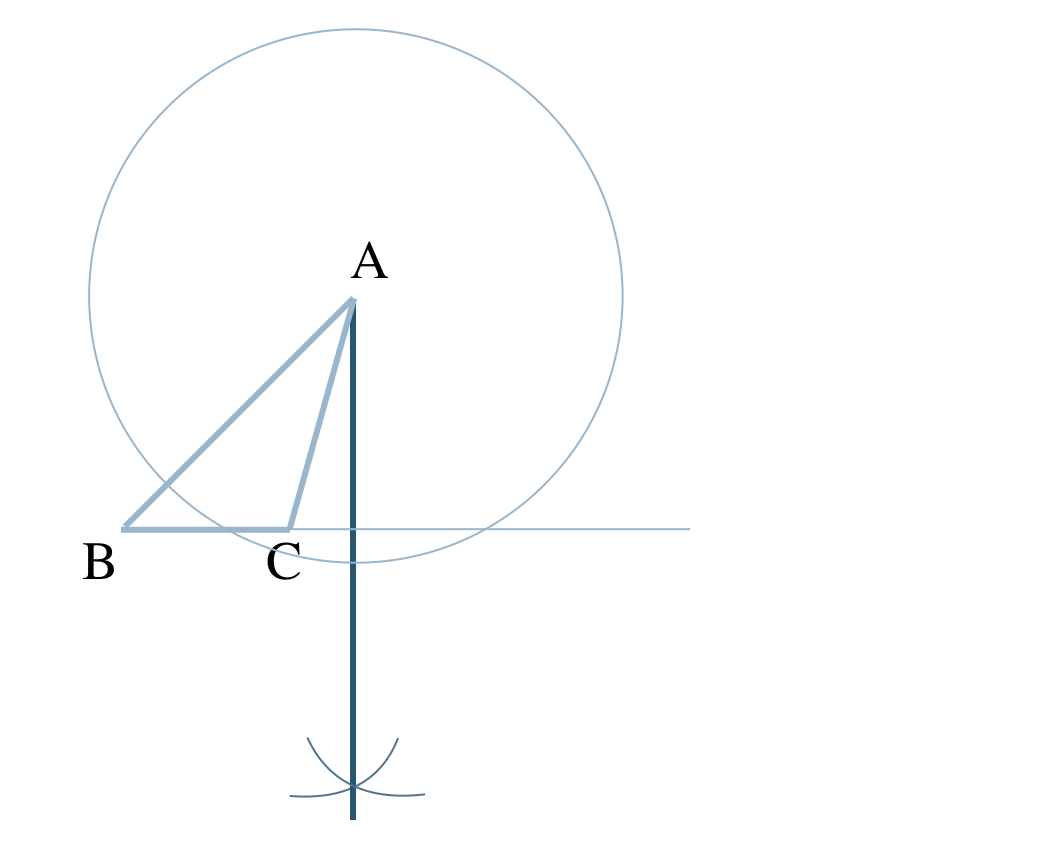
① 辺BCの延長線を引く
② 点Aを中心とする円を描く
(直線BCと交わるように)
③ この円と直線BCとの交点を中心とした等しい半径の円をそれぞれ描き、2つの円の交点をとる
④ 点Aとこの交点を結ぶ
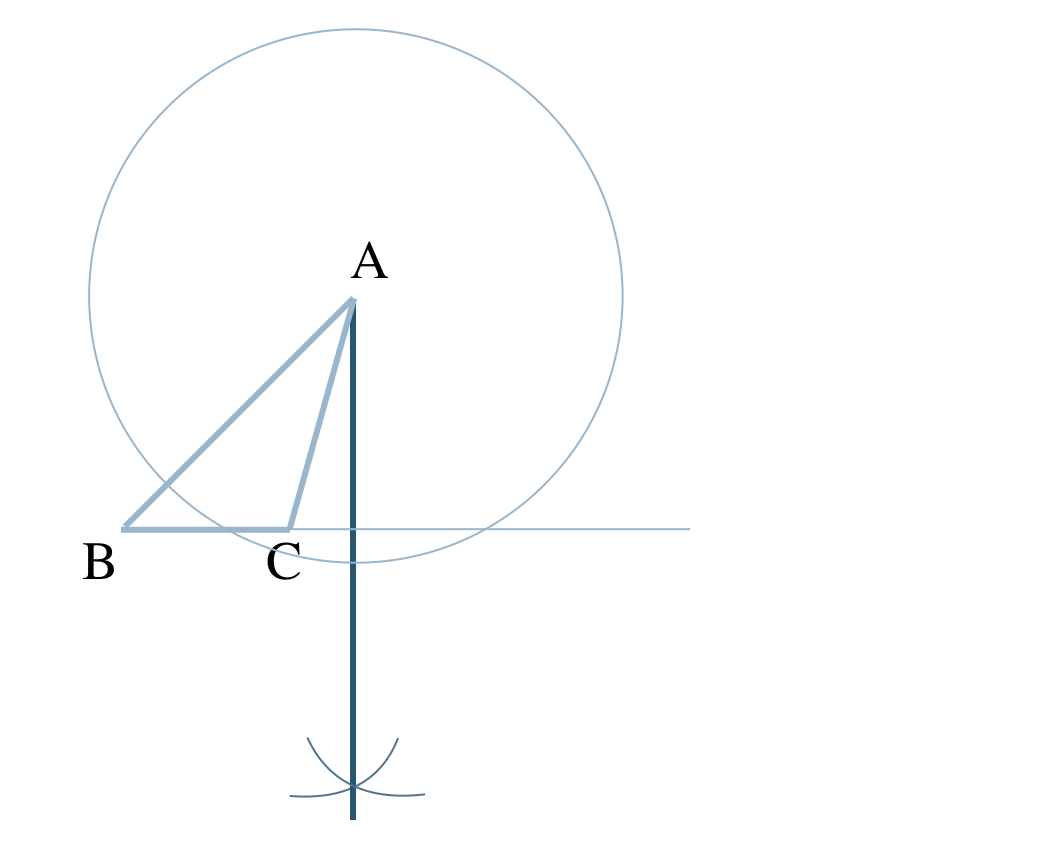
① 辺BCの延長線を引く
② 点Aを中心とする円を描く
(直線BCと交わるように)
③ この円と直線BCとの交点を中心とした等しい半径の円をそれぞれ描き、2つの円の交点をとる
④ 点Aとこの交点を結ぶ
■ 同じタイプの例題解説
» 垂線の作図
» 垂線の作図
3 図形の移動と基本の作図の利用
p.167 1
① 放牧場を中心とした円を描く
(草原と川の境界線と交わるように)
② 境界線との2つの交点を中心とした等しい半径の円をそれぞれ描き、この2つの円の交点をとる
③ この交点と放牧場を結ぶ
(放牧場から境界線への垂線)
④ この直線と境界線との交点を中心として、放牧場と交点までの長さを半径とした円を描く
⑤ 円と直線との交点で、放牧場でない方の点をとる
(放牧場の境界線での対称な点)
⑥ この点と小屋を結ぶ
⑦ この直線と境界線との交点が点P

① 放牧場を中心とした円を描く
(草原と川の境界線と交わるように)
② 境界線との2つの交点を中心とした等しい半径の円をそれぞれ描き、この2つの円の交点をとる
③ この交点と放牧場を結ぶ
(放牧場から境界線への垂線)
④ この直線と境界線との交点を中心として、放牧場と交点までの長さを半径とした円を描く
⑤ 円と直線との交点で、放牧場でない方の点をとる
(放牧場の境界線での対称な点)
⑥ この点と小屋を結ぶ
⑦ この直線と境界線との交点が点P
p.168 問1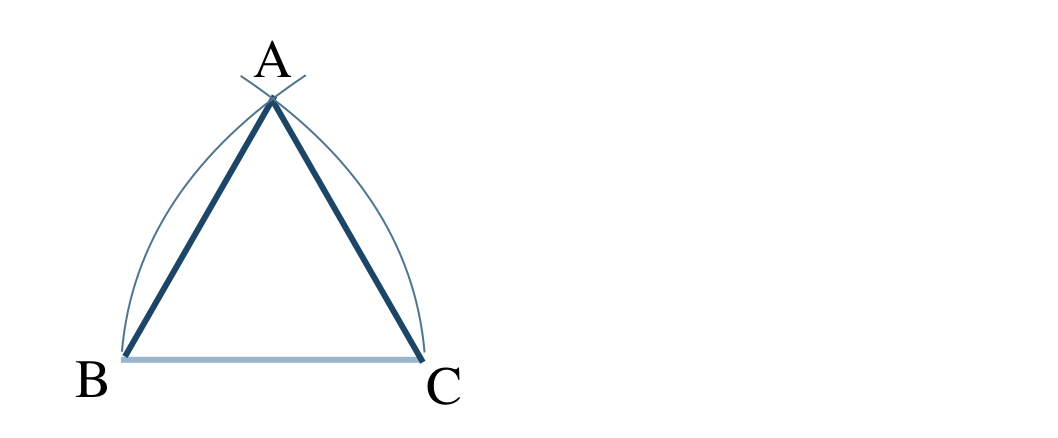
① 線分 \({\rm BC}\) を引く
② 点 \({\rm B}\) が中心、半径が線分 \({\rm BC}\) と等しい円を描く
同様に、点 \({\rm C}\) が中心、半径が線分 \({\rm BC}\) と等しい円を描く
③ 2つの円の交点を \({\rm A}\) とする
④ 線分 \({\rm AB~,~AC}\) を結べば、\(\triangle {\rm ABC}\) が正三角形となる
\(30^\circ\) は正三角形の1つの角が \(60^\circ\) であるので、角の二等分線を引けばよい
また、\(15^\circ\) は \(30^\circ\) の角より、角の二等分線を引けばよい
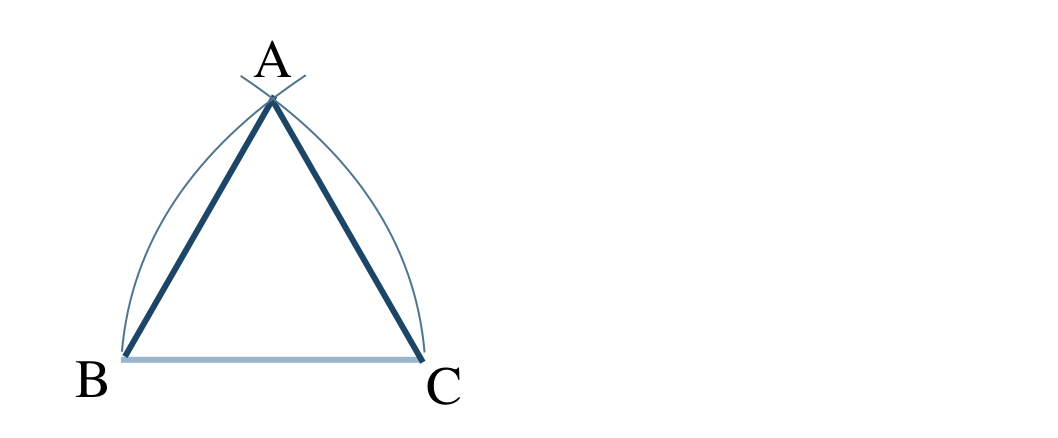
① 線分 \({\rm BC}\) を引く
② 点 \({\rm B}\) が中心、半径が線分 \({\rm BC}\) と等しい円を描く
同様に、点 \({\rm C}\) が中心、半径が線分 \({\rm BC}\) と等しい円を描く
③ 2つの円の交点を \({\rm A}\) とする
④ 線分 \({\rm AB~,~AC}\) を結べば、\(\triangle {\rm ABC}\) が正三角形となる
\(30^\circ\) は正三角形の1つの角が \(60^\circ\) であるので、角の二等分線を引けばよい
また、\(15^\circ\) は \(30^\circ\) の角より、角の二等分線を引けばよい
3節 円とおうぎ形
1 円とおうぎ形の性質
p.170 問1\(\begin{split}~~~{\rm OP}>{\rm OQ}~,~{\rm OP}<{\rm OR}\end{split}\)
■ 同じタイプの例題解説
» 円とおうぎ形
» 円とおうぎ形
p.170 問2\(~~~\) 直径
■ 同じタイプの例題解説
» 円とおうぎ形
» 円とおうぎ形
p.170 問3\(\begin{split}~~~180^\circ\end{split}\)
■ 同じタイプの例題解説
» 円とおうぎ形
» 円とおうぎ形
p.171 問4直径 \(m\) は弦 \({\rm AB}\) の垂直二等分線となる
■ 同じタイプの例題解説
» 円とおうぎ形
» 円とおうぎ形
p.171 問5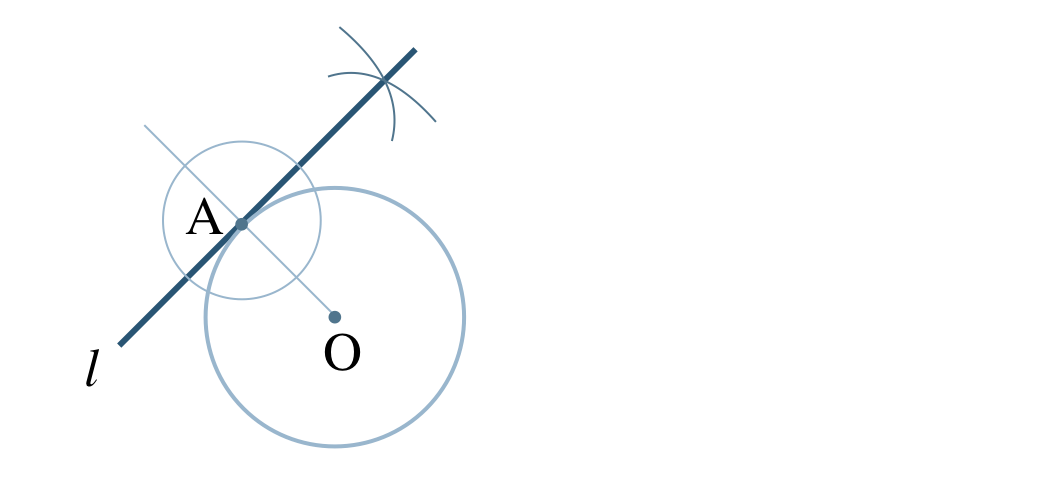
① 点Aと円Oの中心を結ぶ
② 点Aを中心とした円を描く
③ 円と直線OAとの2つの交点を中心とした等しい半径の円をそれぞれ描き、この2つの円の交点をとる
(点Aでの直線OAの垂線を引く)
④ 点Aとこの交点を結ぶ
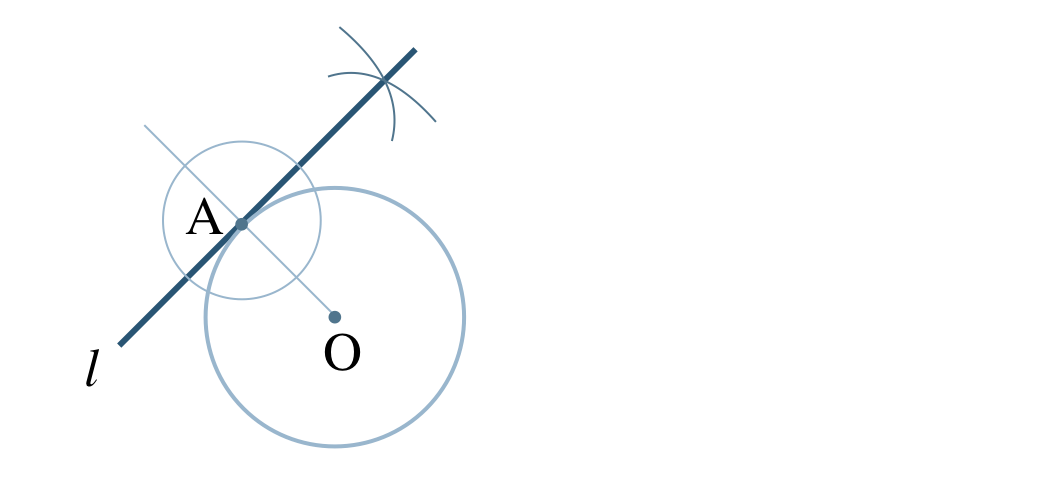
① 点Aと円Oの中心を結ぶ
② 点Aを中心とした円を描く
③ 円と直線OAとの2つの交点を中心とした等しい半径の円をそれぞれ描き、この2つの円の交点をとる
(点Aでの直線OAの垂線を引く)
④ 点Aとこの交点を結ぶ
■ 同じタイプの例題解説
» 円と接線
» 円と接線
p.172 問6\({\small (1)}~\)
① \(3~{\rm cm}\) の線分を引く
② \(3~{\rm cm}\) をコンパスではかり、線分が半径となるような円を描く
③ 線分から \(45^\circ\) をはかり線を引く
④ 残りの円の部分を消す
\({\small (2)}~\)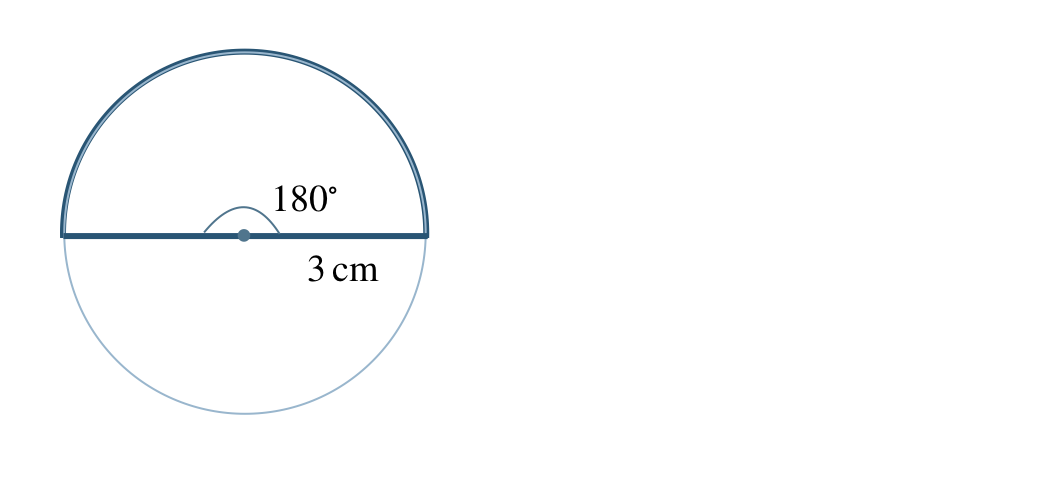
① \(3~{\rm cm}\) の線分を引く
② \(3~{\rm cm}\) をコンパスではかり、線分が半径となるような円を描く
③ 線分を伸ばし、円の直径とする
(中心角が \(180^\circ\) のとき、弦が直径となる)
④ 残りの円の部分を消す
\({\small (3)}~\)
① \(3~{\rm cm}\) の線分を引く
② \(3~{\rm cm}\) をコンパスではかり、線分が半径となるような円を描く
③ 線分を伸ばし、直径とする
④ さらに \(60^\circ\) をはかり、線を引く
⑤ 残りの円の部分を消す

① \(3~{\rm cm}\) の線分を引く
② \(3~{\rm cm}\) をコンパスではかり、線分が半径となるような円を描く
③ 線分から \(45^\circ\) をはかり線を引く
④ 残りの円の部分を消す
\({\small (2)}~\)

① \(3~{\rm cm}\) の線分を引く
② \(3~{\rm cm}\) をコンパスではかり、線分が半径となるような円を描く
③ 線分を伸ばし、円の直径とする
(中心角が \(180^\circ\) のとき、弦が直径となる)
④ 残りの円の部分を消す
\({\small (3)}~\)

① \(3~{\rm cm}\) の線分を引く
② \(3~{\rm cm}\) をコンパスではかり、線分が半径となるような円を描く
③ 線分を伸ばし、直径とする
④ さらに \(60^\circ\) をはかり、線を引く
⑤ 残りの円の部分を消す
2 円とおうぎ形の計量
p.174 問2
\(\begin{split}{\small (1)}~{\frac{1}{3}}\end{split}\) 倍、\(\begin{split}{\frac{1}{3}}\end{split}\) 倍
\(\begin{split}{\small (2)}~{\frac{1}{5}}\end{split}\) 倍、\(\begin{split}{\frac{1}{5}}\end{split}\) 倍
\(\begin{split}{\small (3)}~{\frac{1}{8}}\end{split}\) 倍、\(\begin{split}{\frac{1}{8}}\end{split}\) 倍
\(\begin{split}{\small (1)}~{\frac{1}{3}}\end{split}\) 倍、\(\begin{split}{\frac{1}{3}}\end{split}\) 倍
\(\begin{split}{\small (2)}~{\frac{1}{5}}\end{split}\) 倍、\(\begin{split}{\frac{1}{5}}\end{split}\) 倍
\(\begin{split}{\small (3)}~{\frac{1}{8}}\end{split}\) 倍、\(\begin{split}{\frac{1}{8}}\end{split}\) 倍
■ 同じタイプの例題解説
» 円とおうぎ形の計量
» 円とおうぎ形の計量
p.175 問3\({\small (1)}~\)弧の長さ \(2\pi~{\rm cm}\)、面積 \(6\pi~{\rm cm}^2\)
\({\small (2)}~\)弧の長さ \(5\pi~{\rm cm}\)、面積 \(10\pi~{\rm cm}^2\)
\({\small (2)}~\)弧の長さ \(5\pi~{\rm cm}\)、面積 \(10\pi~{\rm cm}^2\)
■ 同じタイプの例題解説
» 円とおうぎ形の計量
» 円とおうぎ形の計量
p.176 問4\(\begin{split}~~~24\pi~{\rm cm}^2\end{split}\)
■ 同じタイプの例題解説
» 円とおうぎ形の計量
» 円とおうぎ形の計量
p.176 問5
中心角 \(100^\circ\)、面積 \(\begin{split}{\frac{\,45\,}{\,2\,}}\pi~{\rm cm}^2\end{split}\)
中心角 \(100^\circ\)、面積 \(\begin{split}{\frac{\,45\,}{\,2\,}}\pi~{\rm cm}^2\end{split}\)
■ 同じタイプの例題解説
» 円とおうぎ形の計量
» 円とおうぎ形の計量
次のページ「6章 空間図形」


