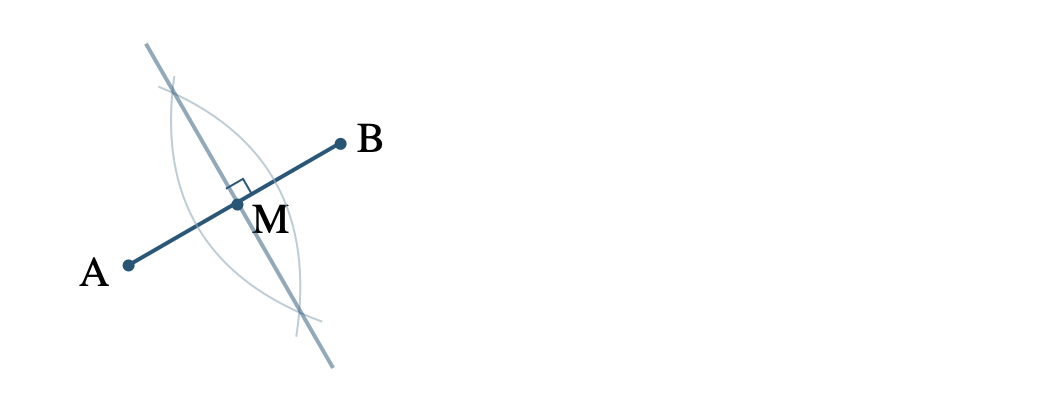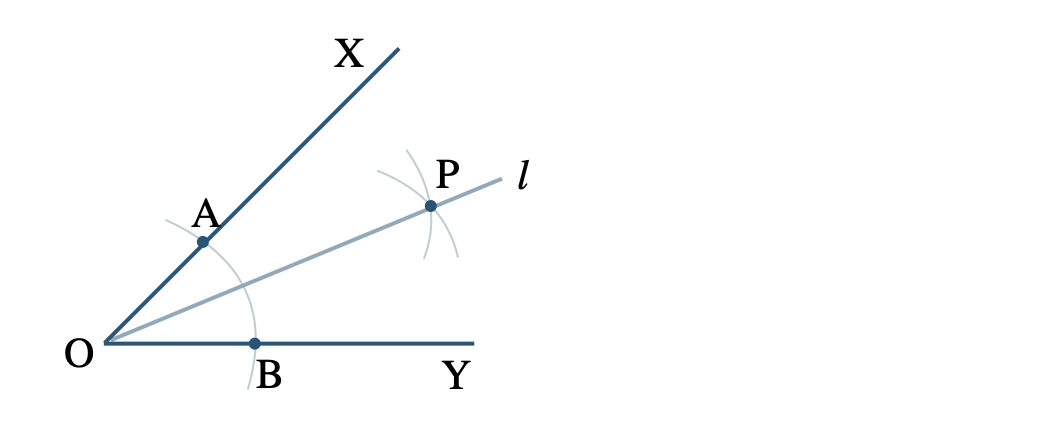【ご注意ください】このページの内容について
このページは、旧版教科書に基づいて作成された内容です。
現在の教科書とは一部内容や表現が異なる場合があります。
順次、最新版に対応したページへと更新を進めておりますので、ご了承ください。
5章 平面図形

文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
日本文教出版中1 1章 正の数と負の数(令和7年度対応)
日本文教出版中1 2章 文字と式(令和7年度対応)
日本文教出版中1 3章 方程式(令和7年度対応)
日本文教出版中1 4章 比例と反比例
日本文教出版中1 5章 平面図形
日本文教出版中1 6章 空間図形
日本文教出版中1 7章 データの活用
5章 平面図形
1節 基本の図形
» 平面上の図形の表し方
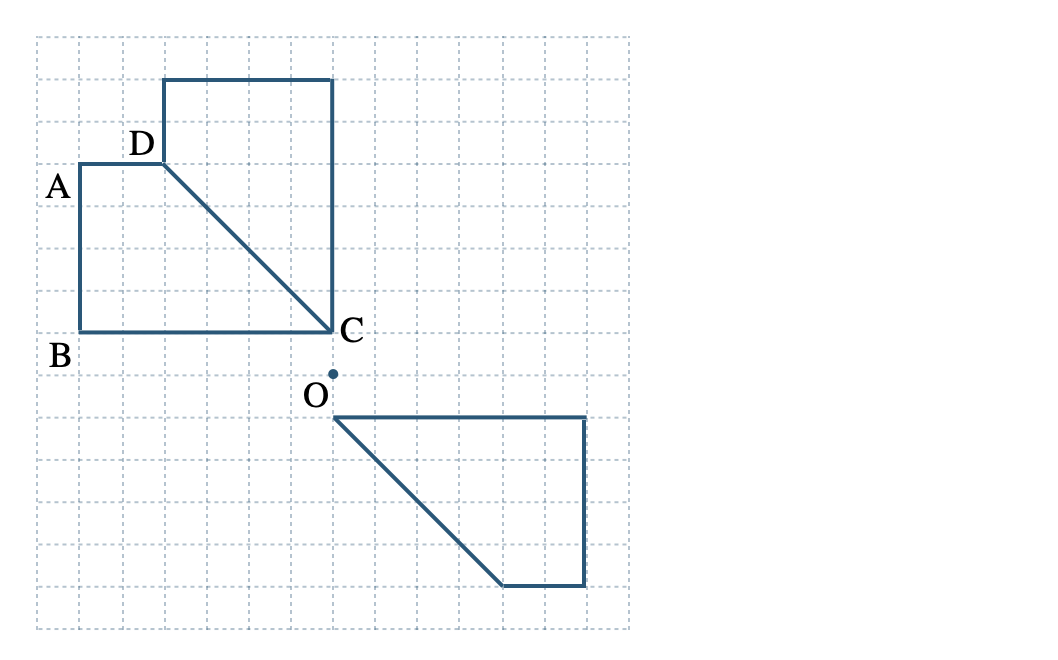
\(\begin{split}{\small (3)}~\triangle {\rm CDE}\end{split}\)
» 平面上の図形の表し方
» 平面上の図形の表し方
» 平面上の図形の表し方
» 平面上の図形の表し方
» 平面上の図形の表し方
» 円と接線
» 円と接線
2節 図形の移動
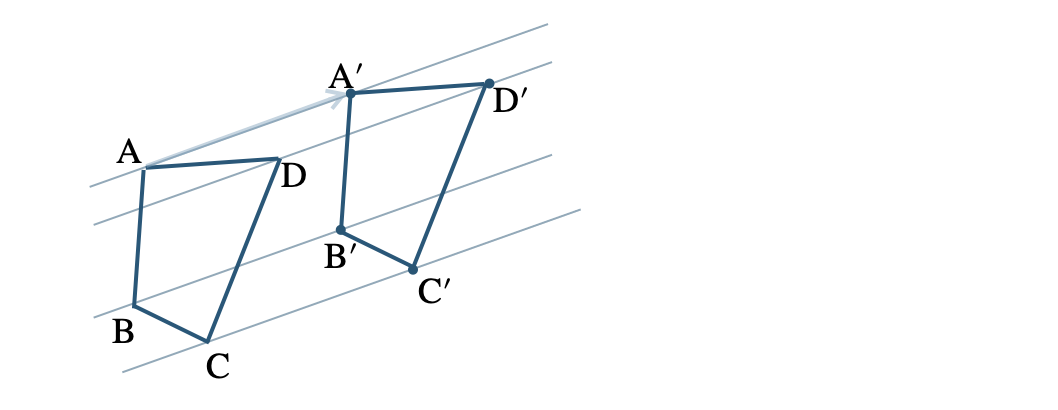
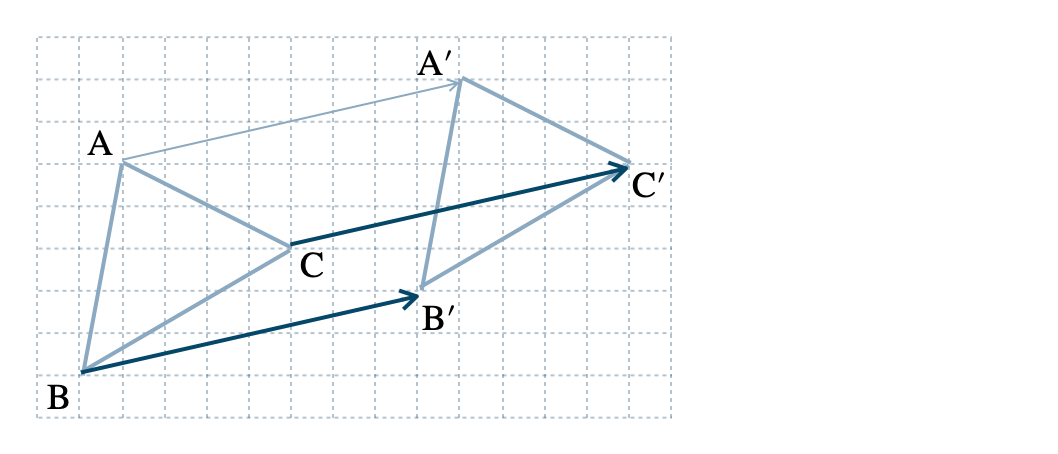
① 線分 \({\rm AA’}\) の長さをはかる
② 点 \({\rm B~,~C~,~D}\) から \({\rm AA’}\) と同じ長さの点 \({\rm B’~,~C’~,~D’}\) をとる
③ 4点をむすんで、四角形 \({\rm A’B’C’D’}\) とする
» 図形の平行移動
\(\angle{\rm AOA’}=\angle{\rm BOB’}=\angle{\rm COC’}=60^\circ\)
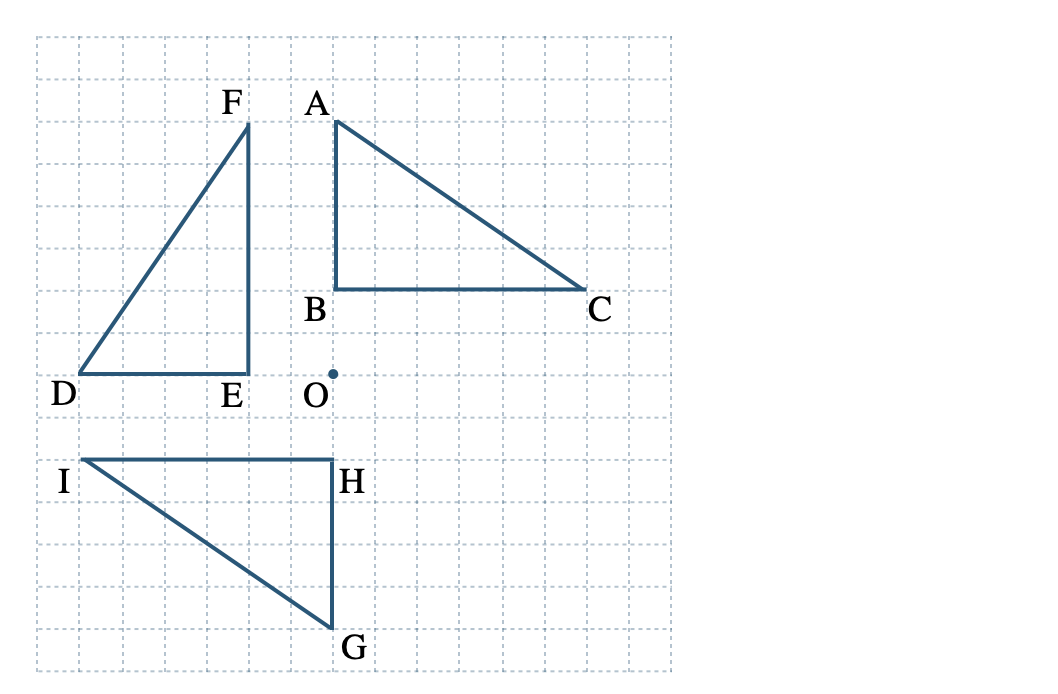
» 図形の回転移動
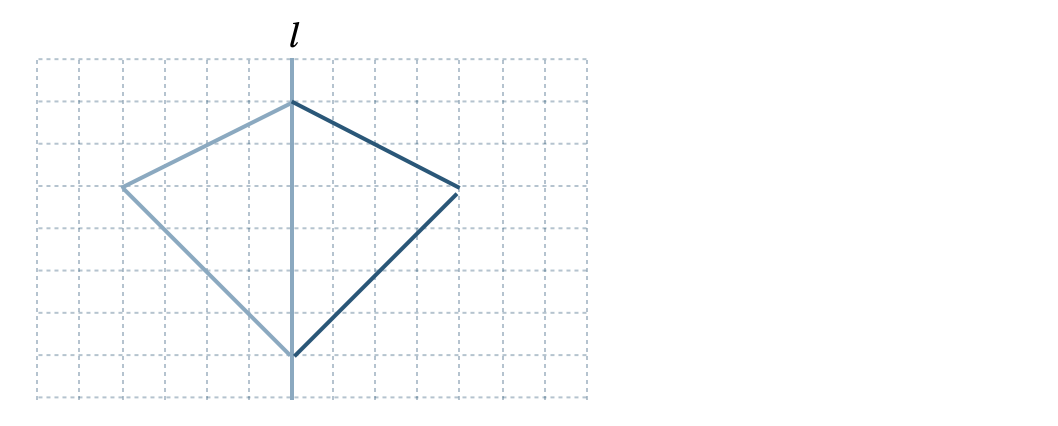
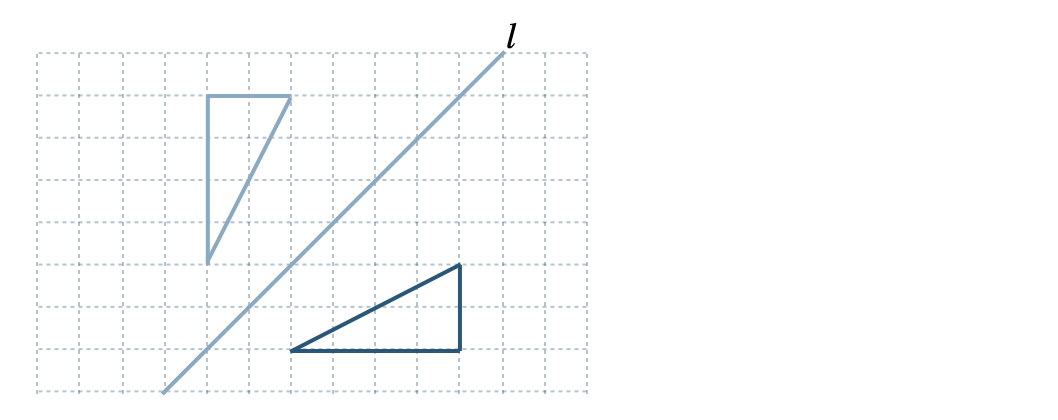
» 図形の対称移動
» 図形の対称移動
基本の問題
\(\begin{split}{\small (2)}~\angle{\rm B}= \angle{\rm Q}\end{split}\)
\(\begin{split}{\small (3)}~{\rm AP=BQ=CR}\end{split}\)
\(\begin{split}{\small (4)}~{\rm AP\,//\,BQ~,~AP\,//\,CR}\end{split}\)
» 図形の平行移動
3節 基本の作図
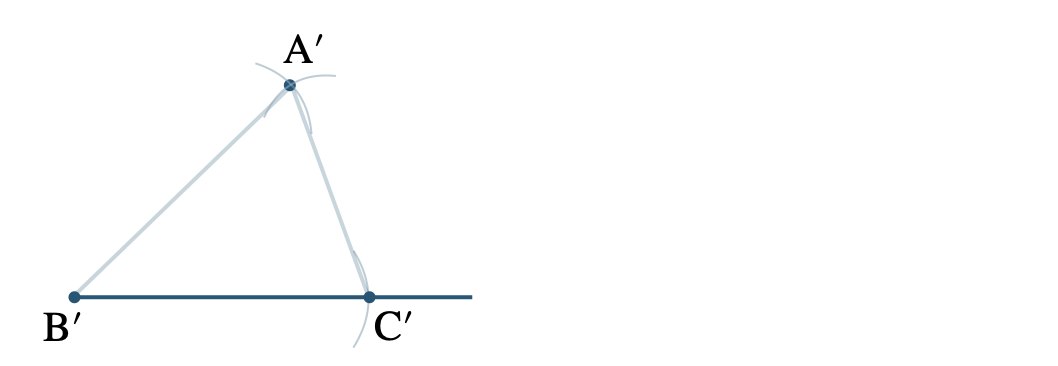
① \({\rm AB}\) の長さをコンパスでとり、点 \({\rm B’}\) を中心とした円をかく
② \({\rm AC}\) の長さをコンパスでとり、点 \({\rm C’}\) を中心とした円をかく
③ この2つの円の交点が \({\rm A’}\) となり、3点をむすぶ
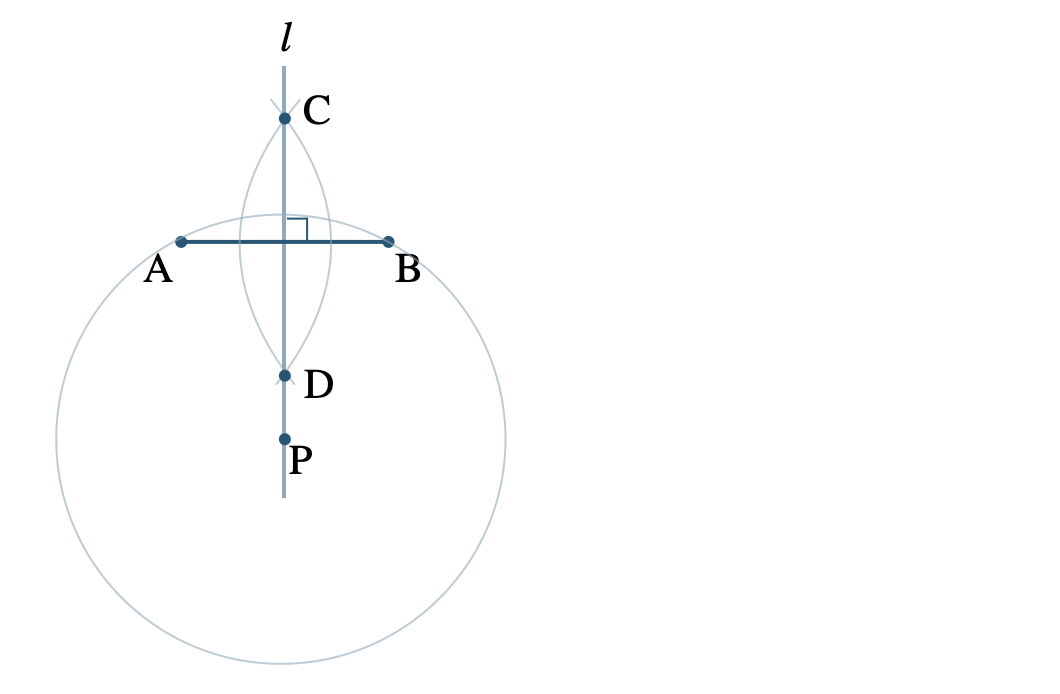
① 点 \({\rm A~,~B}\) を中心として、等しい半径の円をそれぞれ描く
② その2つの円の交点 \({\rm C~,~D}\) をむすぶ直線が \(l\) となる
また、直線 \(l\) 上の点は、点 \({\rm A~,~B}\) からの距離が等しいので、点 \({\rm P}\) を中心として \({\rm PA}\) を半径とする円は点 \({\rm B}\) も通る
» 垂直二等分線の作図

① 点 \({\rm P~,~Q}\) を中心として、等しい半径の円をそれぞれ描く
② その2つの円の交点をむすぶと垂直二等分線となる
③ この垂直二等分線と直線 \(l\) との交点が円 \({\rm O}\) の中心となる
※ 垂直二等分線上の点は、2点 \({\rm P~,~Q}\) からの距離が等しくなるので、半径が \({\rm OP=OQ}\) の円となる
» 垂直二等分線の作図
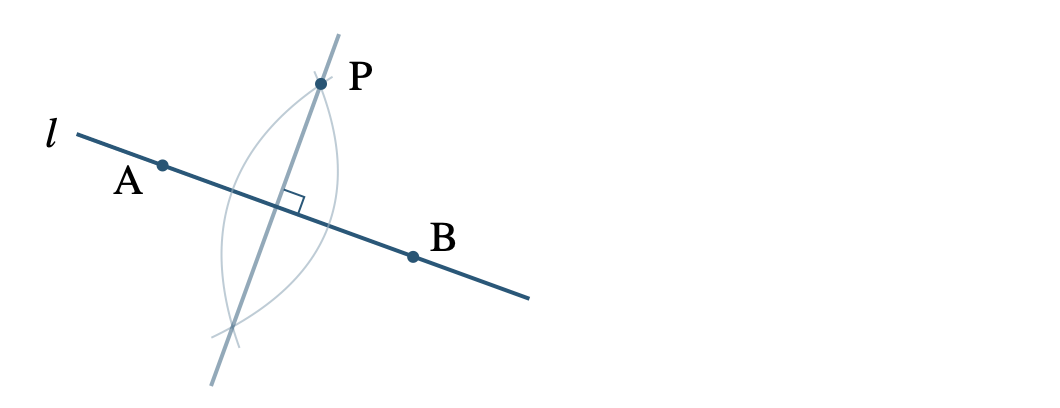
① 直線 \(l\) 上に2点 \({\rm A~,~B}\) をとる
② \({\rm AP}\) を半径とする円を描く
③ \({\rm BP}\) を半径とする円を描く
④ 2つの円の交点を通る直線をひく
» 垂線の作図
② 点 \({\rm A~,~B}\) を中心として等しい半径の円をかき、その交点を \({\rm Q}\) とする。
③ 直線 \({\rm PQ}\) をむすぶと、垂線となる。
» 垂線の作図
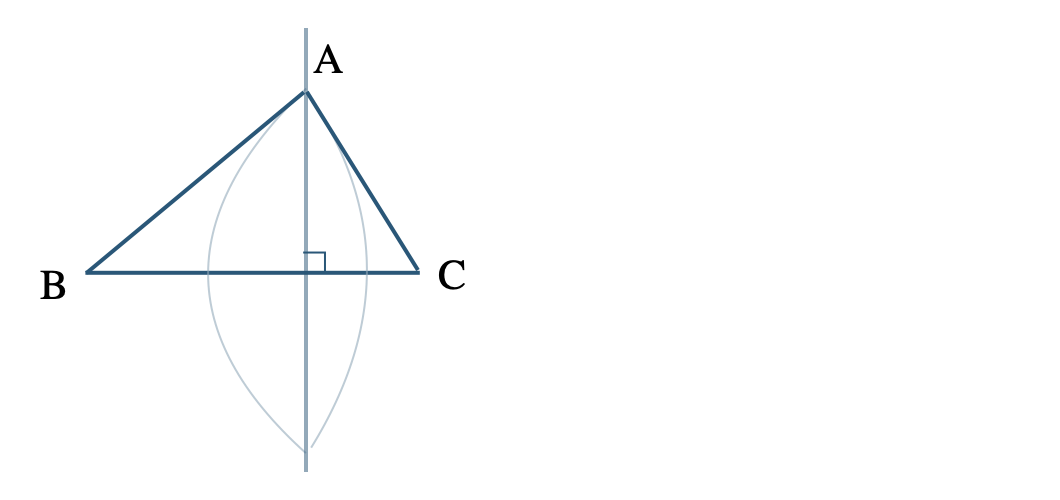
① 点 \({\rm B}\) を中心、半径 \({\rm AB}\) の円を描く
② 点 \({\rm C}\) を中心、半径 \({\rm AC}\) の円を描く
③ 点 \({\rm A}\) と2つの円の交点をむすぶ
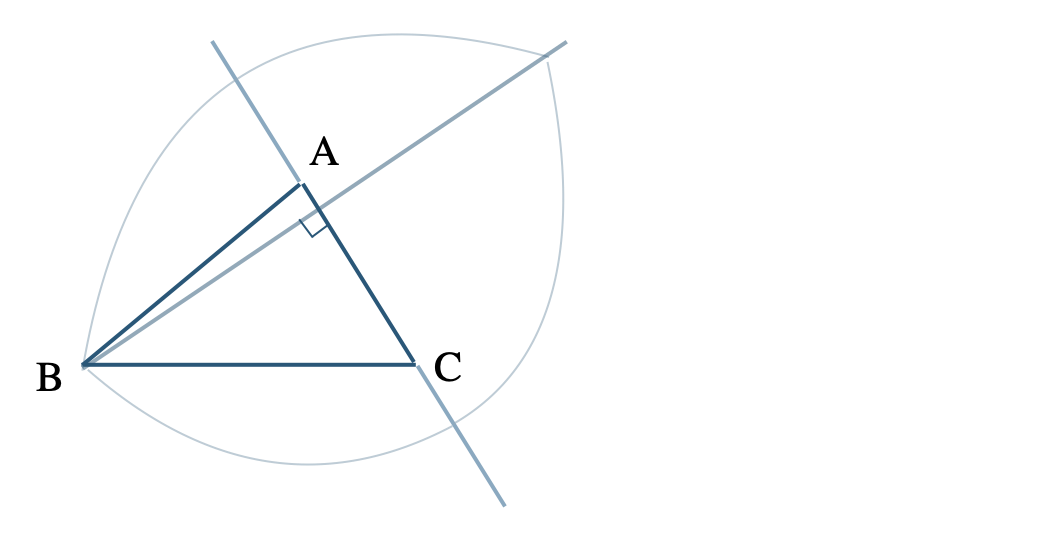
① 辺 \({\rm AC}\) をのばす
② 点 \({\rm A}\) を中心、半径 \({\rm BA}\) の円を描く
③ 点 \({\rm C}\) を中心、半径 \({\rm BC}\) の円を描く
④ 点 \({\rm B}\) と2つの円の交点をむすぶ
» 垂線の作図
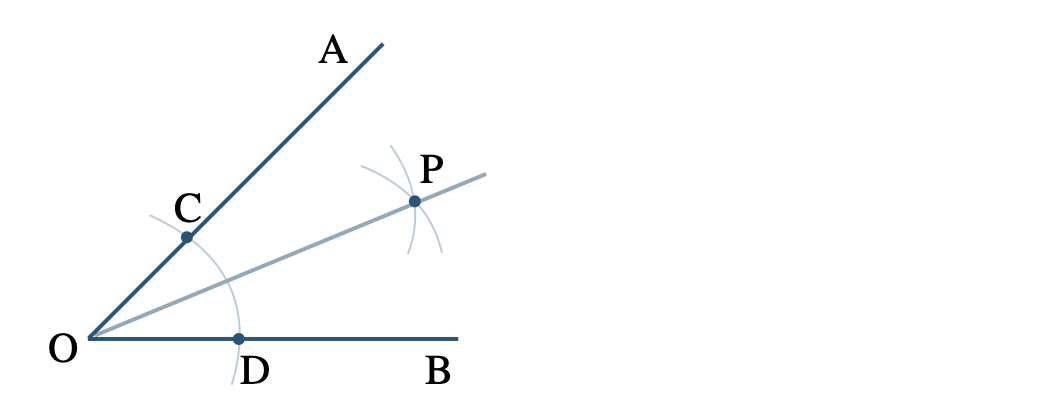
① 点 \({\rm O}\) を中心とする円をかき、その円と \({\rm OA~,~OB}\) との交点をそれぞれ \({\rm C~,~D}\) とする
② 点 \({\rm C~,~D}\) を中心として、等しい半径の円をそれぞれかき、その2つの円の交点を \({\rm P}\) とする
③ 半直線 \({\rm OP}\) をひく
» 角の二等分線の作図
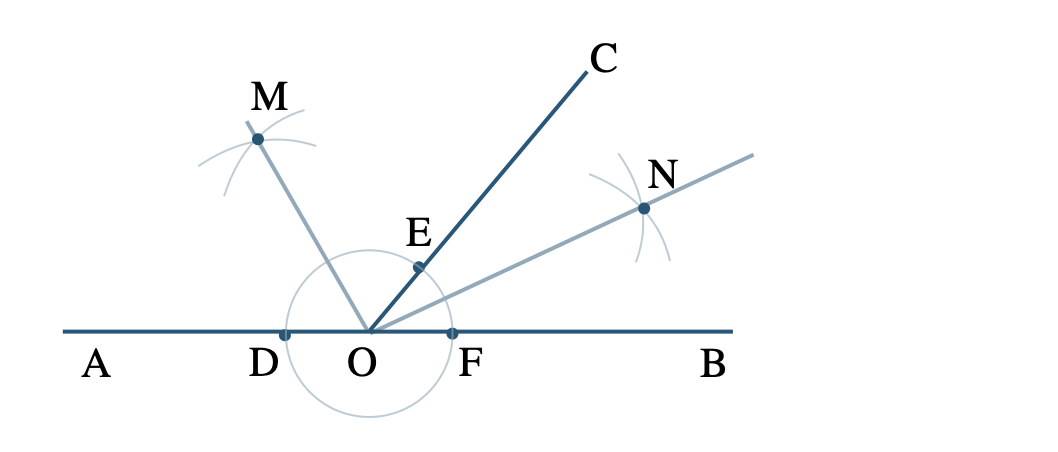
① 点 \({\rm O}\) を中心とする円を描き、\({\rm OA~,~OB~,~OC}\) との交点を \({\rm D~,~E~,~F}\) とする
② 点 \({\rm D~,~E}\) を中心として、等しい半径の円をそれぞれかき、その2つの円の交点を \({\rm M}\) とする
③ 点 \({\rm E~,~F}\) を中心として、等しい半径の円をそれぞれかき、その2つの円の交点を \({\rm N}\) とする
④ 直線 \({\rm OM~,~ON}\) が角の二等分線となる
\(\angle{\rm MON}=90^\circ\)
» 角の二等分線の作図
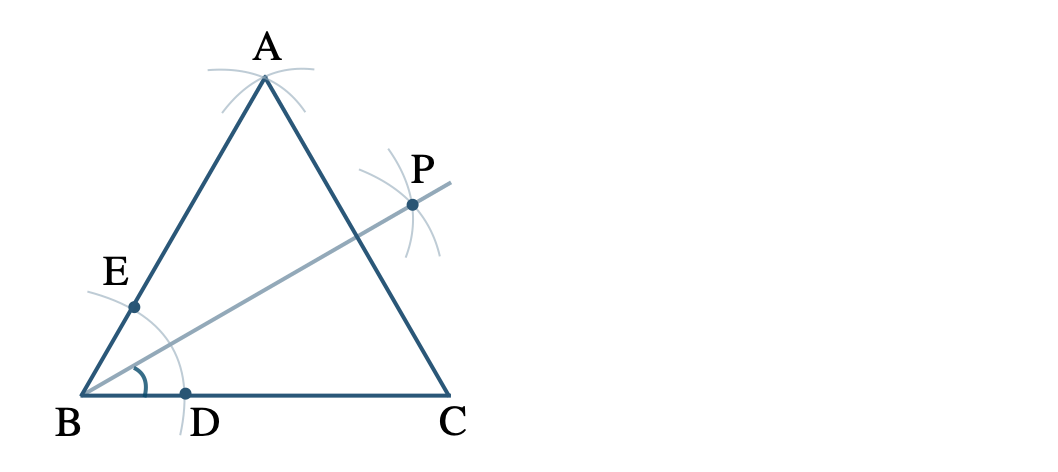
① 線分 \({\rm BC}\) をひく
② 点 \({\rm B}\) が中心、半径が線分 \({\rm BC}\) と等しい円を描く
同様に、点 \({\rm C}\) が中心、半径が線分 \({\rm BC}\) と等しい円を描く
③ 2つの円の交点を \({\rm A}\) とする
④ \(\triangle {\rm ABC}\) が正三角形となり、\(\angle{\rm ABC}=60^\circ\)
⑤ また、\(\angle{\rm ABC}=60^\circ\) の二等分線を引くと、\(\angle{\rm PBC}=30^\circ\)
» 角の二等分線の作図
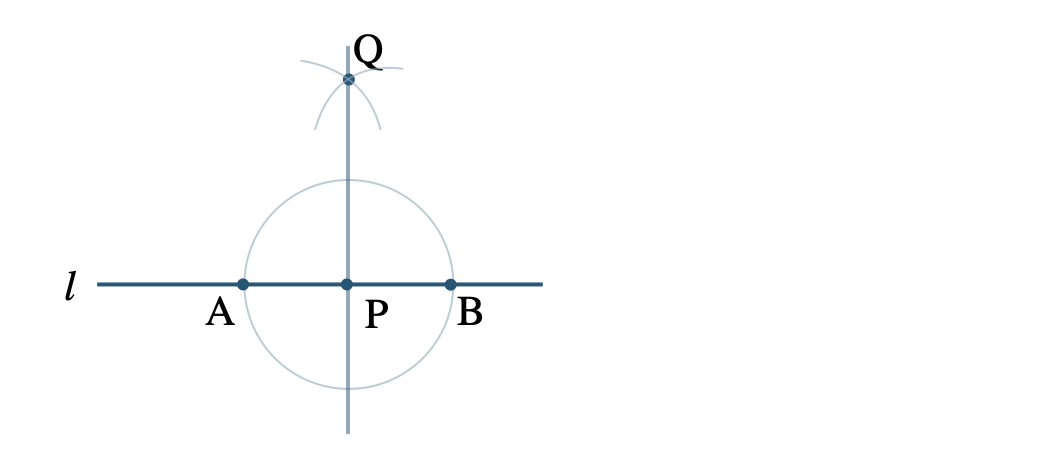
① 点 \({\rm P}\) を中心とした円を描く
② この円と直線 \(l\) との交点を \({\rm A~,~B}\) とする
③ 点 \({\rm A~,~B}\) を中心とした等しい半径の円をそれぞれ描き、交点 \({\rm Q}\) をとる
④ 点 \({\rm P}\) とこの交点 \({\rm Q}\) を結ぶ
» 垂線の作図
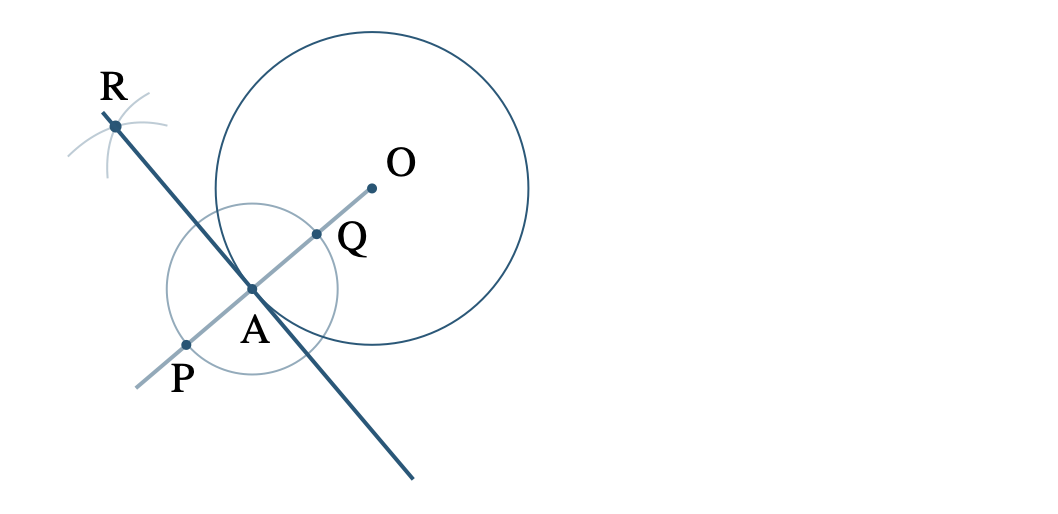
① 半直線 \({\rm OA}\) をひく
② 点 \({\rm A}\) を中心とした円を描き、円と半直線 \({\rm OA}\) との交点を \({\rm P~,~Q}\) とする
③ 点 \({\rm P~,~Q}\) を中心とした、等しい半径の円をそれぞれかき、その2つの円の交点を \({\rm R}\) とする
④ 直線 \({\rm AR}\) をひく
※ 直線 \({\rm OA}\) の点 \({\rm A}\) での垂線を引く
» 円と接線
また、別の2点をとり、この2点を結ぶ線分の垂直二等分線をひく。
この2本の垂直二等分線の交点が円の中心となり、外周までの距離を半径として、もとの円がかける。
» 垂直二等分線の作図
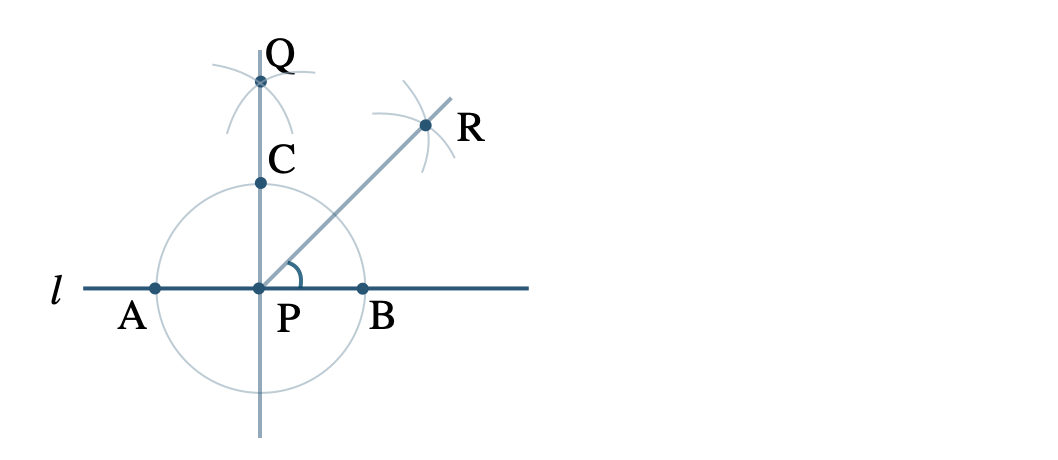
\(\begin{split}{\small (2)}~\end{split}\)点 \({\rm P}\) を中心、\({\rm AB}\) が直径の円となり、\({\rm AB\perp PQ}\) と半径 \({\rm AP=RP}\) より、\(\triangle {\rm ABC}\) は二等辺三角形となる。
よって、\(\angle{\rm RAP}=45^\circ\)
» 垂線の作図
» 角の二等分線の作図
基本の問題
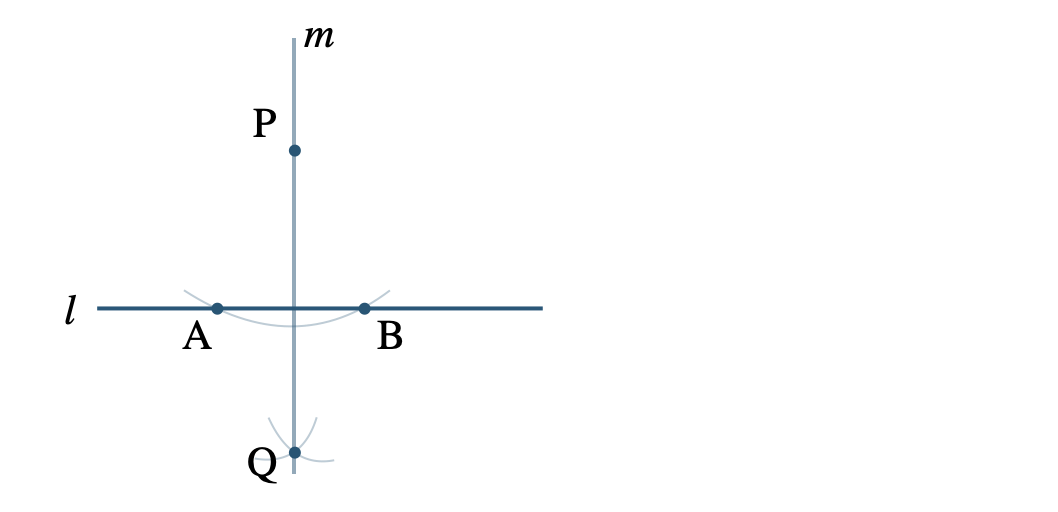
点 \({\rm P}\) を通る垂線を引く
\({\small (2)}~\)

点 \({\rm P}\) を通る直線 \(m\) の垂線を引く
» 垂線の作図
4節 おうぎ形
» 円とおうぎ形の計量
» 円とおうぎ形の計量
» 円とおうぎ形の計量
» 円とおうぎ形の計量
基本の問題
» 円とおうぎ形の計量
» 円とおうぎ形の計量
次のページ「6章 空間図形」