啓林館：未来へ広がる数学１

p.12 問1\({\small (1)}~-3~\)℃　　\({\small (2)}~-2.5~\)℃

p.12 問2\(~~~\)旭川 \(-4.8~\)℃、\(~~~\)札幌 \(-4.3~\)℃
\(~~~\)釧路 \(-4~\)℃、\(~~~\)青森 \(-1~\)℃

p.13 問3\({\small (1)}~-12\)　　\({\small (2)}~+9\)

---

\({\small (3)}~+1.5\)　　\(\begin{split}{\small (4)}~-\frac{\,2\,}{\,3\,}\end{split}\)

---

p.13 問4整数は、\(-5~,~-6~,~4~,~0~,~+12\)
自然数は、\(4~,~+12\)

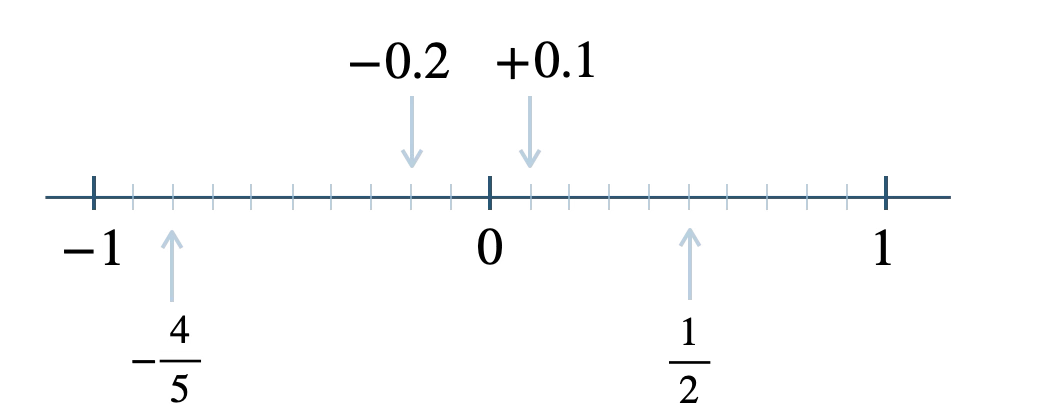
p.14 問5\(~~~\)Ａ \(-4\)、Ｂ \(-1.5\)、Ｃ \(+0.5\)

p.14 問6

p.14 練習問題 1\({\small (1)}~+18\)　　\({\small (2)}~-36\)

---

\(\begin{split}{\small (3)}~+\frac{\,1\,}{\,3\,}\end{split}\)　　\({\small (4)}~-0.8\)

p.14 練習問題 2負の数は、

---

　\(\begin{split}-3.2~,~-10~,~-\frac{\,5\,}{\,6\,}~,~-1~,~-0.1\end{split}\)

---

自然数は、\(\begin{split}+9~,~6\end{split}\)

p.15 問1\(~~~\)\(-500\) 円

p.15 問2\(~~~\)\(-50\) 分

p.16 問3\(~~~\)\(-12~,~+3~,~+27\)

p.16 問4\({\small (1)}~-4\) 個多い　　\({\small (2)}~-6~{\rm cm}\) 長い
\({\small (3)}~-3~{\rm kg}\) 重い　　\({\small (4)}~-10\) 円余る
※ 反対の性質のことばにして、正の数を負の数にする。

p.17 問1\({\small (1)}~\)絶対値 \(5\)、符号を変えた数 \(+5\)
\({\small (2)}~\)絶対値 \(8\)、符号を変えた数 \(-8\)
\({\small (3)}~\)絶対値 \(3.5\)、符号を変えた数 \(+3.5\)

---

\({\small (4)}~\)絶対値 \(\begin{split}\frac{\,3\,}{\,4\,}\end{split}\)、符号を変えた数 \(\begin{split}-\frac{\,3\,}{\,4\,}\end{split}\)

---

p.18 問2\({\small (1)}~\)大きい数 \(3\)、絶対値が大きい数 \(-4\)
\({\small (2)}~\)大きい数 \(-2\)、絶対値が大きい数 \(-5\)

p.18 問3\({\small (1)}~4< 5\)　　\({\small (2)}~-3> -7\)

---

\({\small (3)}~-1.6< -0.6\)　　\(\begin{split}{\small (4)}~-\frac{\,3\,}{\,8\,}> -\frac{\,5\,}{\,8\,}\end{split}\)

---

※ 負の数の大小は絶対値の大小を考えて、その逆となる。

p.19 問4

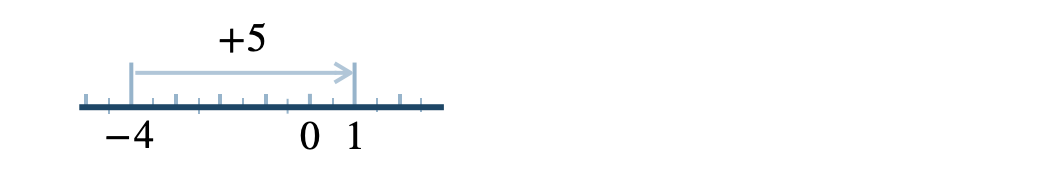
よって、\(-4\) より \(5\) 大きい数は \(1\)

p.19 問5

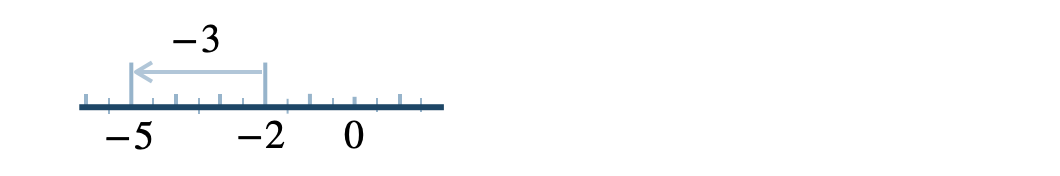
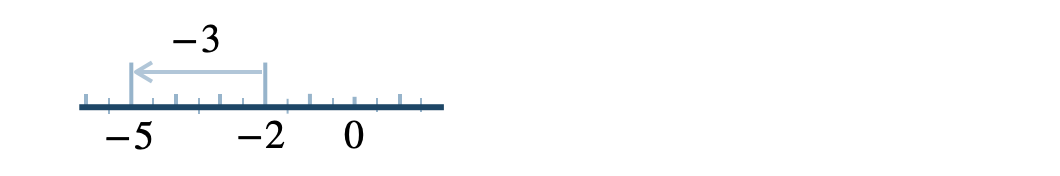
よって、\(-2\) より \(-3\) 大きい数は \(-5\)
※ \(-3\) 大きい数を、\(3\) 小さい数と考える。

p.20 問6\({\small (1)}~-2\)　　\({\small (2)}~2\)　　\({\small (3)}~-3\)　　\({\small (4)}~-5\)
\({\small (5)}~-3\)　　\({\small (6)}~-4\)　　\({\small (7)}~5\)　　\({\small (8)}~4\)
※ \(-4\) 大きい数を、\(4\) 小さい数
　\(-3\) 大きい数を、\(3\) 小さい数
　\(-3\) 小さい数を、\(3\) 大きい数
　\(-8\) 小さい数を、\(8\) 大きい数
　と考える。

p.20 練習問題 1　\(-2~,~-1~,~0~,~1~,~2\)

p.20 練習問題 2　６つ
　\((-4~,~-3~,~-2~,~2~,~3~,~4~)\)

p.20 練習問題 3

---

\({\small (1)}~-0.01> -0.1\)　　\(\begin{split}{\small (2)}~-\frac{\,1\,}{\,2\,}<-\frac{\,1\,}{\,3\,}\end{split}\)

---

\({\small (3)}~-1< -0.6\)

p.20 練習問題 4小さい順は、

---

　\(\begin{split}-\frac{\,8\,}{\,5\,}~,~-1.2~,~-0.5~,~0~,~0.2~,~\frac{\,3\,}{\,5\,}\end{split}\)

---

絶対値が小さい順は、

---

　\(\begin{split}0~,~0.2~,~-0.5~,~\frac{\,3\,}{\,5\,}~,~-1.2~,~-\frac{\,8\,}{\,5\,}\end{split}\)

---

※ \(\begin{split}\frac{\,3\,}{\,5\,}=0.6~,~-\frac{\,8\,}{\,5\,}=-1.6\end{split}\) と考える。

p.20 練習問題 5\({\small (1)}~3\)　　\({\small (2)}~-6\)

p.24 問1\({\small (1)}~-11\)　　\({\small (2)}~-16\)
\({\small (3)}~-61\)　　\({\small (4)}~-24\)

p.24 問2\({\small (1)}~+11\)　　\({\small (2)}~-4\)
\({\small (3)}~-5\)　　\({\small (4)}~-3\)
\({\small (5)}~0\)　　\({\small (6)}~-37\)

p.25 問3\({\small (1)}~(+8)+(-4)=+4\)
\({\small (2)}~(-4)+(-6)=-10\)
\({\small (3)}~(-5)+(-5)=-10\)
\({\small (4)}~(-9)+(+9)=0\)
\({\small (5)}~(-7)+(+9)=+2\)
\({\small (6)}~(+4)+(-10)=-6\)

p.25 問4\({\small (1)}~-0.7\)　　\({\small (2)}~+3\)

---

\(\begin{split}{\small (3)}~-\frac{\,1\,}{\,7\,}\end{split}\)　　\({\small (4)}~-1\)

---

\(\begin{split}{\small (5)}~-\frac{\,7\,}{\,12\,}\end{split}\)　　\(\begin{split}{\small (6)}~-\frac{\,2\,}{\,15\,}\end{split}\)

---

p.27 問5\({\small (1)}~+8\)　　\({\small (2)}~-13\)
\({\small (3)}~+7\)　　\({\small (4)}~0\)
\({\small (5)}~-15\)　　\({\small (6)}~-71\)

p.27 問6\({\small (1)}~-2.2\)　　\({\small (2)}~+5.8\)

---

\(\begin{split}{\small (3)}~+\frac{\,2\,}{\,3\,}\end{split}\)　　\(\begin{split}{\small (4)}~+\frac{\,5\,}{\,6\,}\end{split}\)

---

p.27 問7\({\small (1)}~-2\)　　\({\small (2)}~4\)　　\({\small (3)}~0\)

p.28 問8\({\small (1)}~-3\)　　\({\small (2)}~12\)　　\({\small (3)}~-23\)

p.29 問9　\(\begin{split}&\{3+(-4)\}+(-5)
\\[2pt]~~=~&(-1)+(-5)
\\[2pt]~~=~&-6\end{split}\)
　また、
　\(\begin{split}&3+\{(-4)+(-5)\}
\\[2pt]~~=~&3+(-9)
\\[2pt]~~=~&-6\end{split}\)

p.29 問10\({\small (1)}~-12\)　　\({\small (2)}~10\)
\({\small (3)}~-19\)　　\({\small (4)}~-2\)
\({\small (5)}~-6\)　　\({\small (6)}~-20\)

p.30 練習問題 1\(\begin{split}{\small (1)}~-15\end{split}\)　　\({\small (2)}~8\)　　\({\small (3)}~-100\)
\(\begin{split}{\small (4)}~15\end{split}\)　　\({\small (5)}~-18\)　　\({\small (6)}~0\)
\(\begin{split}{\small (7)}~-8\end{split}\)　　\({\small (8)}~2.5\)　　\({\small (9)}~-2.4\)

---

\(\begin{split}{\small (10)}~-\frac{\,4\,}{\,3\,}\end{split}\)　　\(\begin{split}{\small (11)}~-\frac{\,7\,}{\,10\,}\end{split}\)　　\(\begin{split}{\small (12)}~\frac{\,17\,}{\,24\,}\end{split}\)

---

\(\begin{split}{\small (13)}~-10\end{split}\)　　\({\small (14)}~4\)

p.30 練習問題 2\({\small (1)}~33\)　　\({\small (2)}~-6\)　　\({\small (3)}~-3\)

---

\({\small (4)}~-8.1\)　　\(\begin{split}{\small (5)}~-\frac{\,1\,}{\,6\,}\end{split}\)　　\(\begin{split}{\small (6)}~\frac{\,1\,}{\,28\,}\end{split}\)

---

\({\small (7)}~-10\)　　\({\small (8)}~6\)
\({\small (9)}~0\)　　\({\small (10)}~-33\)

p.30 練習問題 3　イ
※ \(b\) が負の数より、\(-b\) は正の数となる。よって、\(a-b\) はいつでも正の数となる。

p.31 問1\({\small (1)}~-21\)　　\({\small (2)}~-48\)　　\({\small (3)}~-72\)

p.32 問2\({\small (1)}~-30\)　　\({\small (2)}~-72\)　　\({\small (3)}~-100\)

p.33 問3\({\small (1)}~36\)　　\({\small (2)}~56\)　　\({\small (3)}~100\)

p.34 問4\({\small (1)}~-2\)　　\({\small (2)}~-7\)　　\({\small (3)}~4\)

---

\({\small (4)}~8\)　　\(\begin{split}{\small (5)}~-\frac{\,5\,}{\,7\,}\end{split}\)　　\(\begin{split}{\small (6)}~\frac{\,3\,}{\,4\,}\end{split}\)

---

p.35 問5\({\small (1)}~-1.5\)　　\({\small (2)}~0.48\)
\({\small (3)}~-4\)　　\({\small (4)}~-0.05\)

p.35 問6

---

\({\small (1)}~-4\)　　\(\begin{split}{\small (2)}~\frac{\,11\,}{\,3\,}\end{split}\)　　\(\begin{split}{\small (3)}~-\frac{\,4\,}{\,3\,}\end{split}\)

---

p.36 問7

---

\(\begin{split}{\small (1)}~-\frac{\,5\,}{\,2\,}\end{split}\)　　\({\small (2)}~-6\)　　\(\begin{split}{\small (3)}~-\frac{\,1\,}{\,3\,}\end{split}\)

---

p.37 問8

---

\(\begin{split}{\small (1)}~-\frac{\,1\,}{\,12\,}\end{split}\)　　\({\small (2)}~-4\)　　\(\begin{split}{\small (3)}~\frac{\,2\,}{\,3\,}\end{split}\)

---

p.37 問9\(\begin{split}&\{3{\, \small \times \,}(-4)\}{\, \small \times \,}(-5)
\\[2pt]~~=~&(-12){\, \small \times \,}(-5)
\\[2pt]~~=~&60\end{split}\)
　また、
\(\begin{split}&3{\, \small \times \,}\{(-4){\, \small \times \,}(-5)\}
\\[2pt]~~=~&3{\, \small \times \,} 20
\\[2pt]~~=~&60\end{split}\)

p.37 問10\({\small (1)}~-1100\)
※ \(25{\, \small \times \,}(-4)\) を先に計算する。
\({\small (2)}~360\)
※ \((-2){\, \small \times \,}(-15)\) を先に計算する。

p.38 問11

---

\({\small (1)}~-240\)　　\(\begin{split}{\small (2)}~\frac{\,3\,}{\,2\,}\end{split}\)

---

p.39 問12\({\small (1)}~20\)　　\({\small (2)}~-50\)

---

\(\begin{split}{\small (3)}~\frac{\,2\,}{\,7\,}\end{split}\)　　\({\small (4)}~-35\)

---

p.39 練習問題 1\({\small (1)}~-63\)　　\({\small (2)}~-20\)　　\({\small (3)}~0\)
\({\small (4)}~-0.4\)　　\({\small (5)}~0.06\)　　\({\small (6)}~-7\)

p.39 練習問題 2\({\small (1)}~-8\)　　\({\small (2)}~-1\)　　\({\small (3)}~5\)
\({\small (4)}~-20\)　　\({\small (5)}~0\)　　\({\small (6)}~-0.05\)

p.39 練習問題 3

---

\(\begin{split}{\small (1)}~\frac{\,1\,}{\,6\,}\end{split}\)　　\(\begin{split}{\small (2)}~-\frac{\,2\,}{\,3\,}\end{split}\)　　\({\small (3)}~-9\)

p.39 練習問題 4\(\begin{split}{\small (1)}~270\end{split}\)　　\({\small (2)}~-8\)
\(\begin{split}{\small (3)}~24\end{split}\)　　\({\small (4)}~2\)

---

\(\begin{split}{\small (5)}~-\frac{\,5\,}{\,12\,}\end{split}\)　　\(\begin{split}{\small (6)}~-\frac{\,3\,}{\,2\,}\end{split}\)

---

\(\begin{split}{\small (7)}~\frac{\,3\,}{\,2\,}\end{split}\)　　\({\small (8)}~3\)

p.40 問1\({\small (1)}~16\)　　\({\small (2)}~27\)　　\({\small (3)}~32\)

p.40 問2\({\small (1)}~-27\)　　\({\small (2)}~-125\)　　\({\small (3)}~-2.25\)

---

\({\small (4)}~-112\)　　\(\begin{split}{\small (5)}~\frac{\,9\,}{\,2\,}\end{split}\)

---

p.41 問3\({\small (1)}~14\)　　\({\small (2)}~51\)
\({\small (3)}~-58\)　　\({\small (4)}~10\)
\({\small (5)}~-17\)　　\({\small (6)}~2\)

p.41 問4\({\small (1)}~-3\)　　\({\small (2)}~-2\)

p.42 問5\(\begin{split}&\{3+(-4)\}{\, \small \times \,}(-5)
\\[2pt]~~=~&(-1){\, \small \times \,}(-5)
\\[2pt]~~=~&5\end{split}\)
　また、
\(\begin{split}&3{\, \small \times \,}(-5)+(-4){\, \small \times \,}(-5)
\\[2pt]~~=~&-15+20
\\[2pt]~~=~&5\end{split}\)

p.42 練習問題 1\({\small (1)}~72\)　　\({\small (2)}~-3\)
\({\small (3)}~1\)　　\({\small (4)}~5\)

p.42 練習問題 2\({\small (1)}~1\)　　\({\small (2)}~-34\)
\({\small (3)}~-2\)　　\({\small (4)}~-6\)
\({\small (5)}~-8\)　　\({\small (6)}~-12\)

p.42 練習問題 3\({\small (1)}~14\)　　\({\small (2)}~26\)

p.44 問1

---

\(\begin{split}~~~3\div 2=\frac{\,3\,}{\,2\,}=1.5\end{split}\)

---

など、自然数とならないこともある

p.46 問2\(~~~\)(イ)、(エ)

p.47 問3\({\small (1)}~2^2{\, \small \times \,}5\)　　\({\small (2)}~2{\, \small \times \,}3^3\)　　\({\small (3)}~2{\, \small \times \,}3^2{\, \small \times \,}7\)

p.47 問4　\(6\) の倍数は(ウ)、(エ)
　\(14\) の倍数は(ア)、(ウ)、(オ)

p.47 問5\(~~~6\)

p.48 練習問題 1\({\small (1)}~2{\, \small \times \,}3^3{\, \small \times \,}7\)　　\({\small (2)}~2^2{\, \small \times \,}3{\, \small \times \,}5{\, \small \times \,}7\)
\({\small (3)}~3^2{\, \small \times \,}7{\, \small \times \,}11\)

p.48 練習問題 2\(~~~15\)
※ \(540\) を素因数分解して、２乗とならない数の積。

p.48 練習問題 3\(~~~14\)
※ それぞれを素因数分解して、共通している素因数の積。

p.50 問1\(~~~-6~,~-8~,~+7~,~0~,~+2\)

p.51 問2\(~~~\)\(49\) 回

p.51 問3\(~~~51~,~40~,~37~,~55~,~42\)
\(~~~+6~,~-5~,~-8~,~+10~,~-3\)
※ 仮平均が \(45\) であることを読み取る。

p.51 問4\(~~~45\) 回

p.51 練習問題 1\(~~~\)平均 \(155\) 枚
\(~~~\)総売上数 \(1085\) 枚
※ 仮平均 \(150\) との違いの合計が \(+35\) より求める。