東京書籍：新しい数学３

p.131 問1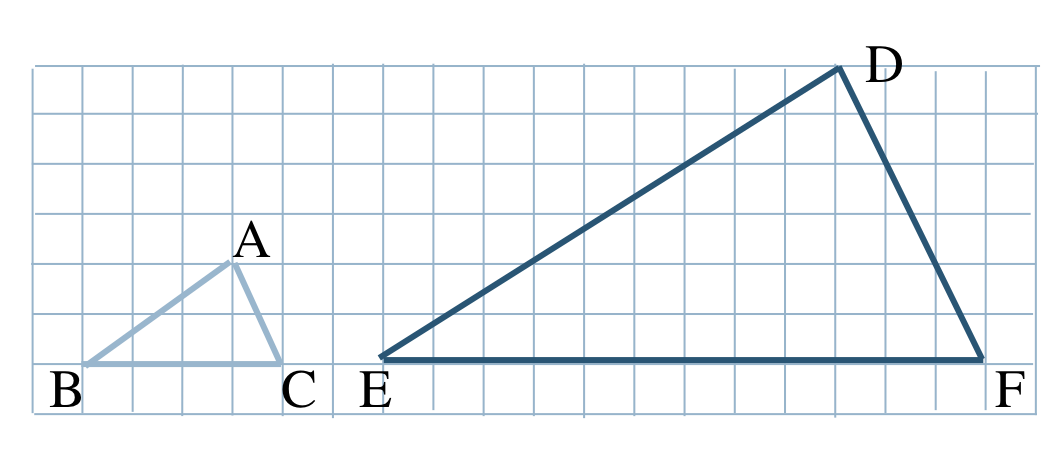
① ＢＣは4マスなので、ＥＦを12マスとる
② ＣからＡまで左1マス上2マスなので、ＦからＤまで左3マス上6マスとる
③ ３点を結ぶ
\(\begin{split}~~~{\rm DE=3AB~,~EF=3BC~,~DF=3AC}\end{split}\)
\(\begin{split}~~~\angle{\rm D}=\angle{\rm A}~,~\angle{\rm E}=\angle{\rm B}~,~\angle{\rm F}=\angle{\rm C}\end{split}\)

p.131 問2\(~~~3\) 倍

p.132 問3\(~~~1~:~2\)

p.132 問4\(~~~\)合同

p.133 問5
① 直線ＢＯ、ＣＯを引く
② ＯからＢＯの長さの２倍の距離に点Ｅをとる
次に、ＯからＣＯの長さの２倍の距離に点Ｆをとる
③ ３点Ｄ、Ｅ、Ｆを結ぶ

p.133 問6
① 点Ｏを内部にとる
（外部でもよいが、内部の方がわかりやすい）
② ＯＡ、ＯＢ、ＯＣ、ＯＤを結ぶ
③ ＯＡ、ＯＢ、ＯＣ、ＯＤのそれぞれの中点をＥ、Ｆ、Ｇ、Hとする
④ その４点を結ぶ

p.134 問7\(\begin{split}~~~{\rm AB}=9~{\rm cm}~,~{\rm EH}=10~{\rm cm}\end{split}\)

p.134 問8\(\begin{split}~~~{\rm AC}=2.3~{\rm cm}\end{split}\)

p.137 問1\(\triangle {\rm ABC}∽\triangle {\rm QRP}\)
\(~~~\)２組の角がそれぞれ等しい

---

\(\triangle {\rm DEF}∽\triangle {\rm TSU}\)
\(~~~\)２組の辺の比とその間の角がそれぞれ等しい

---

\(\triangle {\rm IGH}∽\triangle {\rm JLK}\)
\(~~~\)３組の辺の比がそれぞれ等しい

p.137 問2\({\small (1)}~\triangle {\rm ABC}∽\triangle {\rm ADE}\)
\(~~~\)２組の角がそれぞれ等しい

---

\({\small (2)}~\triangle {\rm ABC}∽\triangle {\rm DEC}\)
\(~~~\)２組の角がそれぞれ等しい

---

\({\small (3)}~\triangle {\rm ABE}∽\triangle {\rm DCE}\)
\(~~~\)２組の辺の比とその間の角がそれぞれ等しい

p.138 問3[証明] \(\triangle {\rm ABC}\) と \(\triangle {\rm DAC}\) において、
仮定より、
\(\begin{split}~~~\angle{\rm BAC}=\angle{\rm ADC}~~~\cdots{\large ①}\end{split}\)
また、\(\angle {\rm C}\) は共通 \(~~~\cdots{\large ②}\)
①、②より、２組の角がそれぞれ等しいから、
\(\begin{split}~~~\triangle {\rm ABC}∽\triangle {\rm DAC}\end{split}\)
[終]

p.138 問4\({\small (1)}~\)[証明] \(\triangle {\rm DAB}\) と \(\triangle {\rm DAC}\) において、
仮定より、
\(\begin{split}~~~\angle{\rm BDA}=\angle{\rm CDA}=90^\circ~~~\cdots{\large ①}\end{split}\)
次に、\(\angle{\rm BDA}=90^\circ\) より、
\(\begin{split}~~~\angle{\rm DBA}=90^\circ-\angle{\rm DAB}\cdots{\large ②}\end{split}\)
また、\(\angle{\rm DAB}+\angle{\rm DAC}=90^\circ\) より、
\(\begin{split}~~~\angle{\rm DAC}=90^\circ-\angle{\rm DAB}\cdots{\large ③}\end{split}\)
よって、②と③より、
\(\begin{split}~~~\angle{\rm DBA}=\angle{\rm DAC}~~~\cdots{\large ④}\end{split}\)
①と④より、２組の角がそれぞれ等しいから、
\(\begin{split}~~~\triangle {\rm DBA}∽\triangle {\rm DAC}\end{split}\)
[終]

---

\({\small (2)}~\)相似な図形の対応する辺の比は等しいから、
\(\begin{split}~~~{\rm AD~:~CD=BD~:~AD}\end{split}\)

p.138 問5[証明] \(\triangle {\rm ABD}\) と \(\triangle {\rm ACE}\) において、
仮定より、
\(\begin{split}~~~\angle{\rm ADB}=\angle{\rm AEC}=90^\circ~~~\cdots{\large ①}\end{split}\)
また、\(\angle {\rm A}\) は共通 \(~~~\cdots{\large ②}\)
①、②より、２組の角がそれぞれ等しいから、
\(\begin{split}~~~\triangle {\rm ABD}∽\triangle {\rm ACE}\end{split}\)
[終]

p.140 問1\(~~~15~{\rm m}\)

p.141 問2\(~~~115≦a< 125\)

p.141 問3\(~~~1.50\times 10^3~{\rm m}\)

p.144 問1\({\small (1)}~\)[証明] \(\triangle {\rm ADE}\) と \(\triangle {\rm ABC}\) において、
\({\rm DE \,//\, BC}\) より、平行線の同位角は等しいから、
\(\begin{split}~~~\angle{\rm ADE}=\angle{\rm ABC}~~~\cdots{\large ①}\end{split}\)
また、\(\angle {\rm A}\) は共通 \(~~~\cdots{\large ②}\)
①、②より、２組の角がそれぞれ等しいから、
\(\begin{split}~~~\triangle {\rm ADE}∽\triangle {\rm ABC}\end{split}\)
[終]

---

\({\small (2)}~{\rm AE:AC~,~DE:BC}\)

p.145 問2\(\begin{split}{\small (1)}~{\rm AE}=12~{\rm cm}\end{split}\)
\(\begin{split}{\small (2)}~{\rm AD:DB}=2:1~,~{\rm AE:EC}=2:1\end{split}\)

p.145 問3[証明] 点Ｄを通り、辺ＡＣに平行な直線をひき、辺ＢＣとの交点をＦとする
\(\triangle {\rm ADE}\) と \(\triangle {\rm DBF}\) において、
\({\rm DE \,//\, BC}\) より、平行線の同位角は等しいから、
\(\begin{split}~~~\angle{\rm ADE}=\angle{\rm DBF}~~~\cdots{\large ①}\end{split}\)
また、\({\rm AE \,//\, DF}\) より、平行線の同位角は等しいから、
\(\begin{split}~~~\angle{\rm DAE}=\angle{\rm BDF}~~~\cdots{\large ②}\end{split}\)
①、②より、２組の角がそれぞれ等しいから、
\(\begin{split}~~~\triangle {\rm ADE}∽\triangle {\rm DBF}\end{split}\)
相似な図形の対応する辺の比は等しいから、
\(\begin{split}~~~{\rm AD:DB=AE:DF}~~~\cdots{\large ③}\end{split}\)
また、四角形ＤＦＣＥは、
\(\begin{split}~~~{\rm DE\,//\,FC~,~DF\,//\,EC}\end{split}\)
これより、平行四辺形である
平行四辺形の２組の対辺はそれぞれ等しいから、
\(\begin{split}~~~{\rm DF=EC}~~~\cdots{\large ④}\end{split}\)
③と④より、
\(\begin{split}~~~{\rm AD:DB=AE:EC}\end{split}\)
[終]

p.146 問4\(\begin{split}{\small (1)}~x=4~,~y=4.8\end{split}\)
\(\begin{split}{\small (2)}~x=2~,~y=5\end{split}\)
\(\begin{split}{\small (3)}~x=10~,~y=4\end{split}\)

p.147 問5[証明] 点Ｃを通り、辺ＡＢに平行な直線をひき、直線ＤＥとの交点をＦとする
\(\triangle {\rm ADE}\) と \(\triangle {\rm CFE}\) において、
対頂角が等しいから、
\(\begin{split}~~~\angle{\rm AED}=\angle{\rm CEF}~~~\cdots{\large ①}\end{split}\)
また、\({\rm AD \,//\, CF}\) より、平行線の錯角は等しいから、
\(\begin{split}~~~\angle{\rm ADE}=\angle{\rm CFE}~~~\cdots{\large ②}\end{split}\)
①、②より、２組の角がそれぞれ等しいから、
\(\begin{split}~~~\triangle {\rm ADE}∽\triangle {\rm CFE}\end{split}\)
相似な図形の対応する辺の比は等しいから、
\(\begin{split}~~~{\rm AD:CF=AE:CE}\end{split}\)
仮定 \({\rm AD:DB=AE:EC}\) より、
\(\begin{split}~~~{\rm DB=CF}\end{split}\)
また、\({\rm DB\,//\,CF}\) であるので、１組の対辺が平行でその長さが等しいから、四角形ＤＢＣＦは平行四辺形である
したがって、
\(\begin{split}~~~{\rm DE\,//\,BC}\end{split}\)
[終]

p.147 問6\(\begin{split}~~~{\rm FD\,//\,AC}\end{split}\)
理由
\(\begin{split}~~~{\rm BF:FA}=6:4.5=4:3\end{split}\)
\(\begin{split}~~~{\rm BD:DC}=8:6=4:3\end{split}\)

p.148 問7\(~~~\)相似比 \(1:2\)
\(~~~\triangle {\rm DED}=2~{\rm cm^2}\)

p.148 問8\(\begin{split}~~~{\rm EF}=2~{\rm cm}~,~{\rm EG}=7~{\rm cm}\end{split}\)

p.152 問1\(\begin{split}{\small (1)}~x=3.6\end{split}\)　　\(\begin{split}{\small (2)}~x=9.6\end{split}\)
\(\begin{split}{\small (3)}~x=7.2\end{split}\)

p.152 問2
① 直線ＡＸを引く
② コンパスを使い、等間隔に点Ｃ、Ｄ、Ｅ、Ｆ、Ｇをとる
③ 直線ＧＢを引き、この直線に平行で点Ｅを通る直線を引く
④ この直線と線分ＡＢの交点が点Ｐとなる

p.153 問3[証明] 線分ＡＤに平行で点Ｃを通る直線を引く
この直線と線分ＡＢとの延長線との交点をＥとする
\({\rm AD \,//\, EC}\) より、平行線の錯角は等しいから、
\(\begin{split}~~~\angle{\rm DAC}=\angle{\rm ACE}~~~\cdots{\large ①}\end{split}\)
\({\rm AD \,//\, EC}\) より、平行線の同位角は等しいから、
\(\begin{split}~~~\angle{\rm BAD}=\angle{\rm AEC}~~~\cdots{\large ②}\end{split}\)
\(\angle{\rm BAD}=\angle{\rm DAC}\) と①、②より、
\(\begin{split}~~~\angle{\rm ACE}=\angle{\rm AEC}\end{split}\)
よって、\(\triangle {\rm ACE}\) は二等辺三角形となるので、
\(\begin{split}~~~{\rm AC=AE}\cdots{\large ③}\end{split}\)
次に、\(\triangle {\rm BEC}\) において、\({\rm AD \,//\, EC}\) より
\(\begin{split}~~~{\rm BA:AE=BD:DC}\end{split}\)
③より、
\(\begin{split}~~~{\rm AB:AC=BD:DC}\end{split}\)
[終]

---

【別解】
辺ＡＣと平行で点Ｂを通る直線を引く
この直線と二等分線ＡＤの延長線との交点をＦとする
\({\rm AC \,//\, BF}\) より、平行線の錯角は等しいから、
\(\begin{split}~~~\angle{\rm DAC}=\angle{\rm BFD}~~~\cdots{\large ①}\end{split}\)
\(\angle{\rm BAD}=\angle{\rm DAC}\) と①より、
\(\begin{split}~~~\angle{\rm BAD}=\angle{\rm BFD}\end{split}\)
よって、\(\triangle {\rm ABF}\) は二等辺三角形となるので、
\(\begin{split}~~~{\rm AB=BF}\cdots{\large ②}\end{split}\)
次に、\(\triangle {\rm BFD}\) と \(\triangle {\rm CAD}\) において、対頂角が等しいから、
\(\begin{split}~~~\angle{\rm BDF}=\angle{\rm CDA}~~~\cdots{\large ③}\end{split}\)
①と③より、２組の角がそれぞれ等しいから、
\(\begin{split}~~~\triangle {\rm BFD}∽\triangle {\rm CAD}\end{split}\)
相似な図形の対応する辺の比は等しいから、
\(\begin{split}~~~{\rm BF:CA=BD:CD}\end{split}\)
②より、
\(\begin{split}~~~{\rm AB:AC=BD:DC}\end{split}\)
[終]

p.156 問1\(\begin{split}~~~\frac{\,8\,}{\,3\,}~{\rm cm^2}\end{split}\)

p.158 問2\(~~~\)周の長さの比 \(~3:5\)
\(~~~\)面積比 \(~9:25\)

p.158 問3\(\begin{split}{\small (1)}~2:5\end{split}\)　　\(\begin{split}{\small (2)}~225~{\rm cm}^2\end{split}\)

p.158 問4(イ) \(~3a\)　　(ウ) \(~5a\)　　(エ) \(~7a\)

p.158 問5ピザの直径の相似比は、
\(\begin{split}~~~24:36=2:3\end{split}\)
よって、面積比は、
\(\begin{split}~~~2^2:3^2=4:9\end{split}\)
また、値段の比は、
\(\begin{split}~~~2200:3600=11:18\end{split}\)
よって、ＭからＬに変えると、面積が \(2.25\) 倍になるのに対して値段が約 \(1.6\) 倍にしかならない
したがって、Ｌサイズの方が得

p.160 問1\(\begin{split}{\small (1)}~9:16\end{split}\)　　\(\begin{split}{\small (2)}~27:64\end{split}\)

p.161 問2\(~~~\)表面積は \(9\) 倍　　体積は \(27\) 倍

p.161 問3\(\begin{split}{\small (1)}~48~{\rm cm^2}\end{split}\)　　\(\begin{split}{\small (2)}~162~{\rm cm^3}\end{split}\)

p.161 問4\(\begin{split}{\small (1)}~32\pi~{\rm cm^3}\end{split}\)　　\(\begin{split}{\small (2)}~1:3\end{split}\)

---

\(\begin{split}{\small (3)}~\frac{\,32\,}{\,27\,}\pi~{\rm cm^3}\end{split}\)