東京書籍：新しい数学２

p.129 問1角の二等分線で分けられた２つの角は等しい

p.130 問2$\begin{split}{\small (1)}~\angle x=45^\circ\end{split}$　　$\begin{split}{\small (2)}~\angle x=50^\circ\end{split}$
$\begin{split}{\small (3)}~\angle x=110^\circ\end{split}$　　$\begin{split}{\small (4)}~\angle x=27^\circ\end{split}$

p.130 問3いってよい

---

鈍角三角形は１つの角が鈍角で、残り２つの角は鋭角である
よって、底角２つが鈍角となることはない

p.131 問4$\begin{split}~~~\angle{\rm ADC}~,~\angle{\rm ADC}~,~90^\circ\end{split}$

p.132 問5${\small (1)}~$[証明]
$\triangle {\rm ACD}$ と $\triangle {\rm BCD}$ において、
仮定より、
$\begin{split}~~~{\rm CA=CB}~~~\cdots{\large ①}\end{split}$
$\begin{split}~~~{\rm DA=DB}~~~\cdots{\large ②}\end{split}$
また、${\rm CD}$ は共通 $~~~\cdots{\large ③}$
①、②、③より、３組の辺がそれぞれ等しいから
$\begin{split}~~~\triangle {\rm ACD}\equiv\triangle {\rm BCD}\end{split}$
合同な図形の対応する角は等しいから
$\begin{split}~~~\angle {\rm ACD}=\angle {\rm BCD}\end{split}$
[終]

---

${\small (2)}~$[証明] $\triangle {\rm CAB}$ は二等辺三角形で (1) の結果より、
$\begin{split}~~~\angle{\rm ACD}=\angle{\rm BCD}\end{split}$
これより、ＣＤは頂角の二等分線となる
二等辺三角形の頂角の二等分線は底辺を垂直に二等分するので、ＣＤは線分ＡＢの垂直二等分線である [終]

p.132 問6$\begin{split}~~~\angle {\rm C}~,~\angle {\rm C}\end{split}$

p.134 問1[証明] $\triangle {\rm ABC}$ 二等辺三角形より、底角が等しいから
$\begin{split}~~~\angle{\rm B}=\angle{\rm C}~~~\cdots{\large ①}\end{split}$
ＢＰは角の二等分線より、
$\begin{split}~~~\angle{\rm PBC}=\angle{\rm B}\times\frac{\,1\,}{\,2\,}\end{split}$
また、ＣＰは角の二等分線より、
$\begin{split}~~~\angle{\rm PCB}=\angle{\rm C}\times\frac{\,1\,}{\,2\,}\end{split}$
よって、①より、
$\begin{split}~~~\angle{\rm B}\times\frac{\,1\,}{\,2\,}=\angle{\rm C}\times\frac{\,1\,}{\,2\,}\end{split}$
したがって、
$\begin{split}~~~\angle{\rm PBC}=\angle{\rm PCB}\end{split}$
三角形の２つの角が等しいから、$\triangle {\rm PBC}$ は二等辺三角形となる [終]

p.134 問2[証明] $\triangle {\rm ABC}$ において、
仮定より、
$\begin{split}~~~\angle{\rm A}=\angle{\rm B}=\angle{\rm C}\end{split}$
$\angle{\rm B}=\angle{\rm C}$ より、$\triangle {\rm ABC}$ は $\angle{\rm A}$ を頂角とする二等辺三角形となるから
$\begin{split}~~~{\rm AB=AC}~~~\cdots{\large ①}\end{split}$
また、$\angle{\rm A}=\angle{\rm C}$ より、$\triangle {\rm ABC}$ は $\angle{\rm B}$ を頂角とする二等辺三角形となるから
$\begin{split}~~~{\rm BA=BC}~~~\cdots{\large ②}\end{split}$
①と②より、
$\begin{split}~~~{\rm AB=BC=AC}\end{split}$
３辺が等しいので正三角形となる
したがって、３つの角が等しい三角形は正三角形である [終]

p.135 問3${\small (1)}~$右の図で、$\angle a=\angle b$ ならば $l \,//\, m$
　正しい

---

${\small (2)}~$２つの三角形の面積が等しいならばこの２つの三角形は合同である
　正しくない

---

${\small (3)}~x> 3$ ならば $x≧5$
　正しくない

p.136 問1${\rm AB=AE}$ より、$\triangle {\rm ABE}$ は二等辺三角形となる
よって、底角が等しいから
$\begin{split}~~~\angle{\rm B}=\angle{\rm E}\end{split}$

---

[証明] $\triangle {\rm ABC}$ と $\triangle {\rm DEF}$ において、
仮定より、
$\begin{split}~~~{\rm AB=DE}~~~\cdots{\large ①}\end{split}$
$\begin{split}~~~{\rm AC=DF}~~~\cdots{\large ②}\end{split}$
$\triangle {\rm ABE}$ が二等辺三角形で底角が等しいから
$\begin{split}~~~\angle{\rm B}=\angle{\rm E}\end{split}$
また、$\angle{\rm C}=\angle{\rm F}=90^\circ$ より、
$\begin{split}~~~\angle{\rm A}=\angle{\rm D}~~~\cdots{\large ③}\end{split}$
①、②、③より、２組の辺とその間の角がそれぞれ等しいから、
$\begin{split}~~~\triangle {\rm ABC}=\triangle {\rm DEF}\end{split}$
[終]

p.137 問2$~~~\triangle {\rm ABC}\equiv\triangle {\rm LKJ}$
直角三角形で、斜辺と他の１辺がそれぞれ等しい

---

$~~~\triangle {\rm DFE}\equiv\triangle {\rm GIH}$
直角三角形で、斜辺と１つの鋭角がそれぞれ等しい

p.138 問3${\small (1)}~$[証明] $\triangle {\rm IBE}$ と $\triangle {\rm IBD}$ において、
仮定より、
$\begin{split}~~~\angle{\rm IEB}=\angle{\rm IDB}=90^\circ~~~\cdots{\large ①}\end{split}$
$\begin{split}~~~\angle{\rm IBE}=\angle{\rm IBD}~~~\cdots{\large ②}\end{split}$
また、${\rm IB}$ は共通 $~~~\cdots{\large ③}$
①、②、③より、直角三角形で、斜辺と１つの鋭角がそれぞれ等しいから
$\begin{split}~~~\triangle {\rm IBE}\equiv\triangle {\rm IBD}\end{split}$
合同な図形の対応する辺は等しいから
$\begin{split}~~~{\rm IE=ID}~~~\cdots{\large ④}\end{split}$
次に、 $\triangle {\rm ICE}$ と $\triangle {\rm ICF}$ においても同様にして、
$\begin{split}~~~{\rm IE=IF}~~~\cdots{\large ⑤}\end{split}$
したがって、④と⑤より、
$\begin{split}~~~{\rm ID=IE=IF}\end{split}$
[終]

---

${\small (2)}~$[証明] $\triangle {\rm AID}$ と $\triangle {\rm AIF}$ において、
仮定より、
$\begin{split}~~~\angle{\rm ADI}=\angle{\rm AFI}=90^\circ~~~\cdots{\large ①}\end{split}$
(1) より、
$\begin{split}~~~{\rm ID=IF}~~~\cdots{\large ②}\end{split}$
また、${\rm AI}$ は共通 $~~~\cdots{\large ③}$
①、②、③より、直角三角形で、斜辺と他の１辺がそれぞれ等しいから
$\begin{split}~~~\triangle {\rm AID}\equiv\triangle {\rm AIF}\end{split}$
合同な図形の対応する角は等しいから
$\begin{split}~~~\angle{\rm DAI}=\angle{\rm FAI}\end{split}$
したがって、$\angle{\rm BAI}=\angle{\rm CAI}$ となり、半直線ＡＩは $\angle{\rm BAC}$ を二等分する [終]

---

${\small (3)}~$

p.140 問1［１］${\rm AB=DC~,~AD=BC}$

---

［２］$\angle{\rm A}=\angle{\rm C}~,~\angle{\rm B}=\angle{\rm D}$

p.141 問2[証明] 対角線 ${\rm AC}$ を引く
平行線の錯角は等しいから
$~~~{\rm AB \,//\, DC}$ より、$\angle{\rm BAC}=\angle{\rm DCA}$
$~~~{\rm AD \,//\, BC}$ より、$\angle{\rm DAC}=\angle{\rm BCA}$
よって、
$\begin{split}~~~\angle{\rm BAC}+\angle{\rm DAC}=\angle{\rm DCA}+\angle{\rm BCA}\end{split}$
これより、
$\begin{split}~~~\angle{\rm A}=\angle{\rm C}~~~\cdots{\large ①}\end{split}$
また、対角線 ${\rm BD}$ を引き、同様にすると、
$\begin{split}~~~\angle{\rm B}=\angle{\rm D}~~~\cdots{\large ②}\end{split}$
①、②より、平行四辺形では２組の対角はそれぞれ等しい [終]

p.141 問3[証明] $\triangle {\rm ABO}$ と $\triangle {\rm CDO}$ において、
平行四辺形では、２組の対辺はそれぞれ等しいから
$\begin{split}~~~{\rm AB=CD}~~~\cdots{\large ①}\end{split}$
また、平行線の錯角が等しいから、${\rm AB \,//\, DC}$ より、
$\begin{split}~~~\angle{\rm BAO}=\angle{\rm DCO}~~~\cdots{\large ②}\end{split}$
$\begin{split}~~~\angle{\rm ABO}=\angle{\rm CDO}~~~\cdots{\large ③}\end{split}$
①、②、③より、１組の辺とその両端の角がそれぞれ等しいから
$\begin{split}~~~\triangle {\rm ABO}\equiv\triangle {\rm CDO}\end{split}$
合同な図形の対応する辺は等しいから、
$\begin{split}~~~{\rm AO=CO~,~BO=DO}\end{split}$
したがって、平行四辺形では、対角線はそれぞれの中点で交わる [終]

p.142 問4${\small (1)}~$

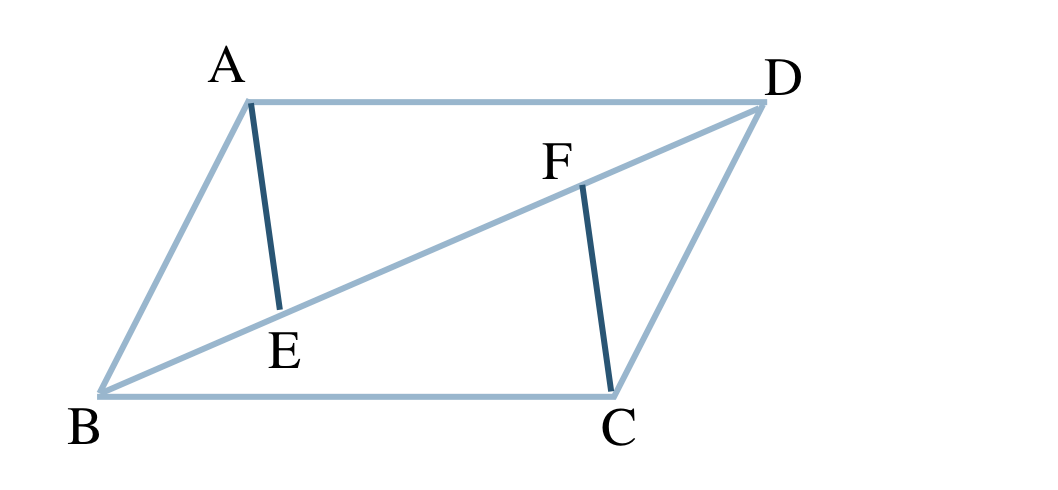
${\small (2)}~$[証明] $\triangle {\rm ABE}$ と $\triangle {\rm CDF}$ において、
仮定より、
$\begin{split}~~~{\rm BE=DF}~~~\cdots{\large ①}\end{split}$
平行四辺形の２組の対辺はそれぞれ等しいから、
$\begin{split}~~~{\rm AB=CD}~~~\cdots{\large ②}\end{split}$
${\rm AB \,//\, CD}$ より、平行線の錯角が等しいから、
$\begin{split}~~~\angle{\rm ABE}=\angle{\rm CDF}~~~\cdots{\large ③}\end{split}$
①、②、③より、２組の辺とその間の角がそれぞれ等しいから、
$\begin{split}~~~\triangle {\rm ABE}\equiv\triangle {\rm CDF}\end{split}$
合同な図形の対応する辺は等しいから、
$\begin{split}~~~{\rm AE=CF}\end{split}$
[終]

p.145 問1[証明] $\triangle {\rm AOB}$ と $\triangle {\rm COD}$ において、
仮定より、
$\begin{split}~~~{\rm AO=CO}~~~\cdots{\large ①}\end{split}$
$\begin{split}~~~{\rm BO=DO}~~~\cdots{\large ②}\end{split}$
対頂角は等しいから
$\begin{split}~~~\angle{\rm AOB}=\angle{\rm COD}~~~\cdots{\large ③}\end{split}$
①、②、③より、２組の辺とその間の角がそれぞれ等しいから、
$\begin{split}~~~\triangle {\rm AOB}\equiv\triangle {\rm COD}\end{split}$
合同な図形の対応する角は等しいから、
$\begin{split}~~~\angle{\rm ABO}=\angle{\rm CDO}\end{split}$
錯角が等しいから、
$\begin{split}~~~{\rm AB \,//\, DC}~~~\cdots{\large ④}\end{split}$
$\triangle {\rm AOD}$ と $\triangle {\rm COB}$ においても同様にすると、
$\begin{split}~~~{\rm AD \,//\, BC}~~~\cdots{\large ⑤}\end{split}$
④、⑤より、この四角形は平行四辺形である
したがって、対角線がそれぞれの中点で交わる四角形は、平行四辺形である [終]

p.146 問2$~~~$ウ

p.147 問3対角線ＡＣを引き、対角線の交点をＯとする
平行四辺形の対角線はそれぞれの中点で交わるから
$\begin{split}~~~{\rm AO=CO}~~~\cdots{\large ①}\end{split}$
$\begin{split}~~~{\rm BO=DO}~~~\cdots{\large ②}\end{split}$
また、仮定より、
$\begin{split}~~~{\rm BE=DF}~~~\cdots{\large ③}\end{split}$
よって、②と③より、
$\begin{split}~~~{\rm BO+BE=DO+DF}\end{split}$
$\begin{split}~~~~~~~~~{\rm EO=FO}\cdots{\large ④}\end{split}$
①、④より、対角線がそれぞれの中点で交わるから、四角形ＡＥＣＦは平行四辺形である [終]

p.147 問4[証明] $\triangle {\rm ABE}$ と $\triangle {\rm CDF}$ において、
仮定より、
$\begin{split}~~~{\rm BE=DF}~~~\cdots{\large ①}\end{split}$
平行四辺形の２組の対辺がそれぞれ等しいから、
$\begin{split}~~~{\rm AB=CD}~~~\cdots{\large ②}\end{split}$
$\begin{split}~~~{\rm BC=DA}~~~\cdots{\large ③}\end{split}$
また、平行四辺形の２組の対角は等しいから、
$\begin{split}~~~\angle{\rm ABE}=\angle{\rm CDF}~~~\cdots{\large ④}\end{split}$
①、②、④より、２組の辺とその間の角がそれぞれ等しいから、
$\begin{split}~~~\triangle {\rm ABE}\equiv\triangle {\rm CDF}\end{split}$
合同な図形の対応する辺は等しいから、
$\begin{split}~~~{\rm AE=CF}~~~\cdots{\large ⑤}\end{split}$
また、①と③より、
$\begin{split}~~~{\rm BC-BE=DA-DE}\end{split}$
$\begin{split}~~~~~~~{\rm EC=FA}~~~\cdots{\large ⑥}\end{split}$
⑤と⑥より、２組の対辺がそれぞれ等しいから、四角形ＡＥＣＦは平行四辺形となる [終]

p.149 問1[証明] ひし形の定義より、４つの辺がすべて等しいから、２組の対辺がそれぞれ等しい
よって、ひし形は平行四辺形である [終]

---

[証明] 正方形の定義より、４つの角がすべて等しいから２つの対角がそれぞれ等しい
よって、正方形は平行四辺形である [終]
（４つの辺がすべて等しいを用いてもよい）

p.149 問2[証明] $\triangle {\rm ABC}$ と $\triangle {\rm DCB}$ において、
長方形の４つの角がすべて等しいから
$\begin{split}~~~\angle{\rm ABC}=\angle{\rm DCB}~~~\cdots{\large ①}\end{split}$
平行四辺形の２組の対辺はそれぞれ等しいから、
$\begin{split}~~~{\rm AB=DC}~~~\cdots{\large ②}\end{split}$
共通な辺より、
$\begin{split}~~~{\rm BC=CB}~~~\cdots{\large ③}\end{split}$
①、②、③より、２組の辺とその間の角がそれぞれ等しいから、
$\begin{split}~~~\triangle {\rm ABC}\equiv\triangle {\rm DCB}\end{split}$
合同な図形の対応する辺は等しいから、
$\begin{split}~~~{\rm AC=DB}\end{split}$
したがって、長方形の対角線は等しい [終]

p.149 問3[証明] $\triangle {\rm ABC}$ と $\triangle {\rm ABC}$ において、
ひし形の４つの辺がすべて等しいから、
$\begin{split}~~~{\rm AB=AD}~~~\cdots{\large ①}\end{split}$
平行四辺形の対角線がそれぞれの中点で交わるから、
$\begin{split}~~~{\rm BO=DO}~~~\cdots{\large ②}\end{split}$
共通な辺より、
$\begin{split}~~~{\rm AO=AO}\cdots{\large ③}\end{split}$
①、②、③より、３組の辺がそれぞれ等しいから、
$\begin{split}~~~\triangle {\rm ABO}\equiv\triangle {\rm ADO}\end{split}$
合同な図形の対応する角は等しいから、
$\begin{split}~~~\angle{\rm BAO}=\angle{\rm DAO}~~~\cdots{\large ④}\end{split}$
①より、$\triangle {\rm ABD}$ は二等辺三角形であり、
④より、ＡＯは頂角の二等分線であるから、
$\begin{split}~~~\angle{\rm AOB}=\angle{\rm AOD}=90^\circ\end{split}$
したがって、ひし形の対角線は垂直に交わる [終]

p.151 問4[証明] 仮定より、斜辺ＡＣの中点がＭより、
$\begin{split}~~~{\rm MA=MC}~~~\cdots{\large ①}\end{split}$
また、長方形の対角線は等しいから、
$\begin{split}~~~{\rm AC=BD}~~~\cdots{\large ②}\end{split}$
平行四辺形の対角線はそれぞれの中点で交わるから、
$\begin{split}~~~{\rm MB=MD}~~~\cdots{\large ③}\end{split}$
②より、
$\begin{split}~~~{\rm MA+MC=MB+MD}\end{split}$
①、③より、
$\begin{split}~~~{\rm 2MA=2MB}\end{split}$
$\begin{split}~~~~{\rm MA=MB}~~~\cdots{\large ④}\end{split}$
したがって、①と④より、
$\begin{split}~~~{\rm MA=MB=MC}\end{split}$
[終]

p.150 問5${\small (1)}~$正しくない
反例は、

対角線が等しい四角形でも、平行四辺形でなければ長方形ではない

---

${\small (2)}~$正しくない
反例は、

対角線が垂直に交わる四角形でも、平行四辺形でなければひし形ではない

p.150 問6${\small (1)}~$ア　　　${\small (2)}~$エ
${\small (3)}~$イ　　　${\small (4)}~$ウ

p.153 問1$\begin{split}~~~\triangle {\rm ABM}=\triangle {\rm BDM}=\triangle {\rm MDC}\end{split}$

---

$\begin{split}~~~\triangle {\rm ABC}=\triangle {\rm BDC}=\triangle {\rm ABD}\end{split}$
$\begin{split}~~~~~~~~~~~~~~=\triangle {\rm ACD}=\triangle {\rm AMD}\end{split}$

p.154 問2２点Ａ、Ｃを結ぶ
直線ＡＣに平行で点Ｂを通る直線ＤＥを引く
直線ＡＥを引くと、この直線が境界線となる
（$\triangle {\rm ABC}=\triangle {\rm AEC}$となるから）