このページは教科書改訂(令和7年度、2025年度)に対応済みの内容です。
このページは、学校図書:中学校数学1
3章 1次方程式(令和7年度対応)
3章 1次方程式(令和7年度対応)

教科書に完全対応の問題集|教科書ぴったりトレーニング
教科書に対応した数学の問題集|教科書ぴったりトレーニングの紹介 こんにちは、みなさん!今回は中学生の...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
学校図書中1 1章 正の数・負の数(令和7年度対応)
学校図書中1 2章 文字式(令和7年度対応)
学校図書中1 3章 1次方程式(令和7年度対応)
学校図書中1 4章 比例と反比例
学校図書中1 5章 平面図形
学校図書中1 6章 空間図形
学校図書中1 7章 データの活用
3章 1次方程式
1 方程式
p.99 問1 \(5x+3> 2x+4\)
■ 同じタイプの問題の解説
→ 大小関係を表す式
→ 大小関係を表す式
p.100 問2\(\begin{split}{\small (1)}~3a+2b> 300\end{split}\)
\(\begin{split}{\small (2)}~3a+5b=40\end{split}\)
\(\begin{split}{\small (3)}~\frac{\,3600\,}{\,x\,}< 15\end{split}\)
\(\begin{split}{\small (4)}~3x+5=17\end{split}\)
\(\begin{split}{\small (2)}~3a+5b=40\end{split}\)
\(\begin{split}{\small (3)}~\frac{\,3600\,}{\,x\,}< 15\end{split}\)
\(\begin{split}{\small (4)}~3x+5=17\end{split}\)
■ 同じタイプの問題の解説
→ 等しい関係を表す式
→ 等しい関係を表す式
■ 同じタイプの問題の解説
→ 大小関係を表す式
→ 大小関係を表す式
p.101 問3\(\begin{split}{\small (1)}~a+b≧30\end{split}\)
\(\begin{split}{\small (2)}~40a+180≦500\end{split}\)
\(\begin{split}{\small (3)}~\frac{\,x\,}{\,5\,}≧2\end{split}\)
\(\begin{split}{\small (4)}~a-25≦10\end{split}\)
\(\begin{split}{\small (2)}~40a+180≦500\end{split}\)
\(\begin{split}{\small (3)}~\frac{\,x\,}{\,5\,}≧2\end{split}\)
\(\begin{split}{\small (4)}~a-25≦10\end{split}\)
■ 同じタイプの問題の解説
→ 大小関係を表す式
→ 大小関係を表す式
p.101 問4\(\begin{split}{\small (1)}~\end{split}\)大人 \(2\) 人、中学生 \(1\) 人の入園料の合計は \(1250\) 円
\(\begin{split}{\small (2)}~\end{split}\)大人 \(3\) 人の入園料の合計は、中学生 \(5\) 人の入園料の合計より高い
\(\begin{split}{\small (2)}~\end{split}\)大人 \(3\) 人の入園料の合計は、中学生 \(5\) 人の入園料の合計より高い
■ 同じタイプの問題の解説
→ 関係の表す式の意味
→ 関係の表す式の意味
p.101 問5\(\begin{split}{\small (1)}~\end{split}\)縦の長さは横の長さより長い
\(\begin{split}{\small (2)}~\end{split}\)長方形の面積は \(48~{\rm cm}^2\)
\(\begin{split}{\small (3)}~\end{split}\)長方形の周りの長さは \(32~{\rm cm}\) 以下
\(\begin{split}{\small (2)}~\end{split}\)長方形の面積は \(48~{\rm cm}^2\)
\(\begin{split}{\small (3)}~\end{split}\)長方形の周りの長さは \(32~{\rm cm}\) 以下
■ 同じタイプの問題の解説
→ 関係の表す式の意味
→ 関係の表す式の意味
p.102 問1\(2\)、\(3{\, \small \times \,}2+2=8\)、\(<\)、\(2+10=12\)
\(3\)、\(3{\, \small \times \,}3+2=11\)、\(<\)、\(3+10=13\)
\(4\)、\(3{\, \small \times \,}4+2=14\)、\(=\)、\(4+10=14\)
\(5\)、\(3{\, \small \times \,}5+2=17\)、\(>\)、\(5+10=15\)
クリップ \(1\) 個の重さは \(4~{\rm g}\)
\(3\)、\(3{\, \small \times \,}3+2=11\)、\(<\)、\(3+10=13\)
\(4\)、\(3{\, \small \times \,}4+2=14\)、\(=\)、\(4+10=14\)
\(5\)、\(3{\, \small \times \,}5+2=17\)、\(>\)、\(5+10=15\)
クリップ \(1\) 個の重さは \(4~{\rm g}\)
■ 同じタイプの問題の解説
→ 方程式とその解
→ 方程式とその解
p.103 問2\(\begin{split}{\small (1)}~x=5\end{split}\) \(\begin{split}{\small (2)}~x=4\end{split}\)
■ 同じタイプの問題の解説
→ 方程式とその解
→ 方程式とその解
p.106 問1\(\begin{split}{\small (1)}~\end{split}\)左辺に \(x=-8\) を代入すると、
\(\begin{split}~-8+6=-2\end{split}\)
よって、右辺と等しくなるので、
\(x=-8\) は解である
\(\begin{split}{\small (2)}~\end{split}\)左辺に \(x=7\) を代入すると、
\(\begin{split}~7-3=4\end{split}\)
よって、右辺と等しくなるので、
\(x=7\) は解である
\(\begin{split}~-8+6=-2\end{split}\)
よって、右辺と等しくなるので、
\(x=-8\) は解である
\(\begin{split}{\small (2)}~\end{split}\)左辺に \(x=7\) を代入すると、
\(\begin{split}~7-3=4\end{split}\)
よって、右辺と等しくなるので、
\(x=7\) は解である
■ 同じタイプの問題の解説
→ 方程式とその解
→ 方程式とその解
p.106 問2\(\begin{split}{\small (1)}~x=6\end{split}\) \(\begin{split}{\small (2)}~x=-9\end{split}\)
\(\begin{split}{\small (3)}~x=9\end{split}\) \(\begin{split}{\small (4)}~x=-6\end{split}\)
\(\begin{split}{\small (3)}~x=9\end{split}\) \(\begin{split}{\small (4)}~x=-6\end{split}\)
■ 同じタイプの問題の解説
→ 等式の性質
→ 等式の性質
p.106 問3\(\begin{split}{\small (1)}~x=8\end{split}\) \(\begin{split}{\small (2)}~x=-6\end{split}\)
\(\begin{split}{\small (3)}~x=10\end{split}\) \(\begin{split}{\small (4)}~x=\frac{\,1\,}{\,2\,}\end{split}\)
\(\begin{split}{\small (5)}~x=15\end{split}\) \(\begin{split}{\small (6)}~x=-30\end{split}\)
\(\begin{split}{\small (7)}~x=16\end{split}\) \(\begin{split}{\small (8)}~x=-7\end{split}\)
\(\begin{split}{\small (3)}~x=10\end{split}\) \(\begin{split}{\small (4)}~x=\frac{\,1\,}{\,2\,}\end{split}\)
\(\begin{split}{\small (5)}~x=15\end{split}\) \(\begin{split}{\small (6)}~x=-30\end{split}\)
\(\begin{split}{\small (7)}~x=16\end{split}\) \(\begin{split}{\small (8)}~x=-7\end{split}\)
■ 同じタイプの問題の解説
→ 等式の性質
→ 等式の性質
p.106 問4 たとえば、\(x+1=9\) など
■ 同じタイプの問題の解説
→ 等式の性質
→ 等式の性質
p.108 問5\(\begin{split}{\small (1)}~\end{split}\)左辺に \(x=-3\) を代入すると、
\(\begin{split}~3{\, \small \times \,}(-3)+5=-9+5=-4\end{split}\)
よって、右辺と等しくなるので、
\(x=-3\) は解である
\(\begin{split}{\small (2)}~\end{split}\)左辺に \(x=2\) を代入すると、
\(\begin{split}~5{\, \small \times \,}2=10\end{split}\)
右辺に \(x=2\) を代入すると、
\(\begin{split}~-2{\, \small \times \,}2+14=-4+14=10\end{split}\)
よって、左辺と右辺が等しくなるので、
\(x=2\) は解である
\(\begin{split}~3{\, \small \times \,}(-3)+5=-9+5=-4\end{split}\)
よって、右辺と等しくなるので、
\(x=-3\) は解である
\(\begin{split}{\small (2)}~\end{split}\)左辺に \(x=2\) を代入すると、
\(\begin{split}~5{\, \small \times \,}2=10\end{split}\)
右辺に \(x=2\) を代入すると、
\(\begin{split}~-2{\, \small \times \,}2+14=-4+14=10\end{split}\)
よって、左辺と右辺が等しくなるので、
\(x=2\) は解である
p.108 問6\(\begin{split}{\small (1)}~x=4\end{split}\) \(\begin{split}{\small (2)}~x=-2\end{split}\)
\(\begin{split}{\small (3)}~x=-3\end{split}\) \(\begin{split}{\small (4)}~x=8\end{split}\)
\(\begin{split}{\small (3)}~x=-3\end{split}\) \(\begin{split}{\small (4)}~x=8\end{split}\)
■ 同じタイプの問題の解説
→ 1次方程式の解き方
→ 1次方程式の解き方
p.108 問7\(\begin{split}{\small (1)}~x=4\end{split}\) \(\begin{split}{\small (2)}~x=5\end{split}\)
\(\begin{split}{\small (3)}~x=-2\end{split}\) \(\begin{split}{\small (4)}~x=-3\end{split}\)
\(\begin{split}{\small (5)}~x=9\end{split}\) \(\begin{split}{\small (6)}~x=-\frac{\,1\,}{\,2\,}\end{split}\)
\(\begin{split}{\small (3)}~x=-2\end{split}\) \(\begin{split}{\small (4)}~x=-3\end{split}\)
\(\begin{split}{\small (5)}~x=9\end{split}\) \(\begin{split}{\small (6)}~x=-\frac{\,1\,}{\,2\,}\end{split}\)
■ 同じタイプの問題の解説
→ 1次方程式の解き方
→ 1次方程式の解き方
p.109 問8\(\begin{split}{\small (1)}~x=8\end{split}\) \(\begin{split}{\small (2)}~x=-3\end{split}\)
\(\begin{split}{\small (3)}~x=-2\end{split}\) \(\begin{split}{\small (4)}~x=0\end{split}\)
\(\begin{split}{\small (3)}~x=-2\end{split}\) \(\begin{split}{\small (4)}~x=0\end{split}\)
■ 同じタイプの問題の解説
→ かっこのある1次方程式
→ かっこのある1次方程式
p.109 問9\(\begin{split}{\small (1)}~x=-20\end{split}\) \(\begin{split}{\small (2)}~x=-2\end{split}\)
■ 同じタイプの問題の解説
→ 小数や分数をふくむ1次方程式
→ 小数や分数をふくむ1次方程式
p.110 問10\(\begin{split}{\small (1)}~x=-10\end{split}\) \(\begin{split}{\small (2)}~x=5\end{split}\)
\(\begin{split}{\small (3)}~x=-5\end{split}\) \(\begin{split}{\small (4)}~x=13\end{split}\)
\(\begin{split}{\small (3)}~x=-5\end{split}\) \(\begin{split}{\small (4)}~x=13\end{split}\)
■ 同じタイプの問題の解説
→ 小数や分数をふくむ1次方程式
→ 小数や分数をふくむ1次方程式
確かめよう
p.111 確かめよう 1\(\begin{split}{\small (1)}~80-3x=5\end{split}\)
\(\begin{split}{\small (2)}~7a> 40\end{split}\)
\(\begin{split}{\small (3)}~120x+200=160y\end{split}\)
\(\begin{split}{\small (4)}~4x≦20\end{split}\)
\(\begin{split}{\small (2)}~7a> 40\end{split}\)
\(\begin{split}{\small (3)}~120x+200=160y\end{split}\)
\(\begin{split}{\small (4)}~4x≦20\end{split}\)
■ 同じタイプの問題の解説
→ 等しい関係を表す式
→ 等しい関係を表す式
■ 同じタイプの問題の解説
→ 大小関係を表す式
→ 大小関係を表す式
p.111 確かめよう 2 イ
■ 同じタイプの問題の解説
→ 方程式とその解
→ 方程式とその解
p.111 確かめよう 3\(\begin{split}{\small (1)}~x=3\end{split}\) \(\begin{split}{\small (2)}~x=-7\end{split}\)
\(\begin{split}{\small (3)}~x=-6\end{split}\) \(\begin{split}{\small (4)}~x=27\end{split}\)
\(\begin{split}{\small (3)}~x=-6\end{split}\) \(\begin{split}{\small (4)}~x=27\end{split}\)
■ 同じタイプの問題の解説
→ 等式の性質
→ 等式の性質
p.111 確かめよう 4\(\begin{split}{\small (1)}~x=4\end{split}\) \(\begin{split}{\small (2)}~x=6\end{split}\)
\(\begin{split}{\small (3)}~x=3\end{split}\) \(\begin{split}{\small (4)}~x=-1\end{split}\)
\(\begin{split}{\small (5)}~x=1\end{split}\) \(\begin{split}{\small (6)}~x=3\end{split}\)
\(\begin{split}{\small (3)}~x=3\end{split}\) \(\begin{split}{\small (4)}~x=-1\end{split}\)
\(\begin{split}{\small (5)}~x=1\end{split}\) \(\begin{split}{\small (6)}~x=3\end{split}\)
■ 同じタイプの問題の解説
→ 1次方程式の解き方
→ 1次方程式の解き方
■ 同じタイプの問題の解説
→ かっこのある1次方程式
→ かっこのある1次方程式
※ p.112 の計算力を高めよう1の解答は、教科書 p.303~304 にあります。
2 1次方程式の利用
p.114 問1\(\begin{split}{\small (1)}~\end{split}\)
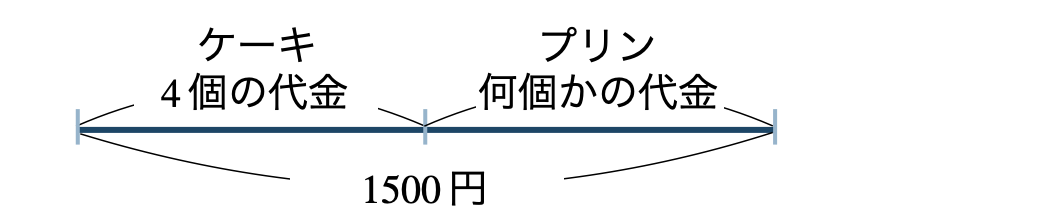
\(\begin{split}{\small (2)}~\end{split}\)プリンの個数を \(x\) 個とすると、
\(240{\, \small \times \,}4+90{\, \small \times \,}x=1500\)
\(\begin{split}{\small (3)}~x=6\end{split}\)
\(\begin{split}{\small (4)}~\end{split}\)プリンを \(6\) 個買うと、
\(\begin{split}&240{\, \small \times \,}4+90{\, \small \times \,}6
\\[2pt]~~=~&960+540
\\[2pt]~~=~&1500
\end{split}\)
これは問題に適する
よって、プリンは \(6\) 個買った

(ケーキ \(4\) 個の代金)
+(プリン何個かの代金)= \(1500\) 円
\(\begin{split}{\small (2)}~\end{split}\)プリンの個数を \(x\) 個とすると、
\(240{\, \small \times \,}4+90{\, \small \times \,}x=1500\)
\(\begin{split}{\small (3)}~x=6\end{split}\)
\(\begin{split}{\small (4)}~\end{split}\)プリンを \(6\) 個買うと、
\(\begin{split}&240{\, \small \times \,}4+90{\, \small \times \,}6
\\[2pt]~~=~&960+540
\\[2pt]~~=~&1500
\end{split}\)
これは問題に適する
よって、プリンは \(6\) 個買った
■ 同じタイプの問題の解説
→ 1次方程式と代金
→ 1次方程式と代金
p.114 問2\(\begin{eqnarray}~~~150-x&=&x+30
\\[2pt]~~~x&=&60
\end{eqnarray}\)
妹のリボンは \(60~{\rm cm}\)
\\[2pt]~~~x&=&60
\end{eqnarray}\)
妹のリボンは \(60~{\rm cm}\)
■ 同じタイプの問題の解説
→ 1次方程式と整数・割合
→ 1次方程式と整数・割合
p.117 問5そのままではいけない
\(\begin{eqnarray}~~~60{\, \small \times \,}(x+15)&=&240x
\\[2pt]~~~x&=&5
\end{eqnarray}\)
これより、\(5\) 分後に追いつくことになるが、
\(240{\, \small \times \,}5=1200\)
これより、追いつく前に妹は \(1~{\rm km}\) 離れた駅に追いついてしまう
\(\begin{eqnarray}~~~60{\, \small \times \,}(x+15)&=&240x
\\[2pt]~~~x&=&5
\end{eqnarray}\)
これより、\(5\) 分後に追いつくことになるが、
\(240{\, \small \times \,}5=1200\)
これより、追いつく前に妹は \(1~{\rm km}\) 離れた駅に追いついてしまう
■ 同じタイプの問題の解説
→ 1次方程式と速さ
→ 1次方程式と速さ
p.118 問1
\(\begin{split}{\small (1)}~\frac{\,3\,}{\,4\,}\end{split}\) \(\begin{split}{\small (2)}~\frac{\,7\,}{\,5\,}\end{split}\)
\(\begin{split}{\small (3)}~\frac{\,3\,}{\,4\,}\end{split}\) \(\begin{split}{\small (4)}~3\end{split}\)
\(\begin{split}{\small (1)}~\frac{\,3\,}{\,4\,}\end{split}\) \(\begin{split}{\small (2)}~\frac{\,7\,}{\,5\,}\end{split}\)
\(\begin{split}{\small (3)}~\frac{\,3\,}{\,4\,}\end{split}\) \(\begin{split}{\small (4)}~3\end{split}\)
■ 同じタイプの問題の解説
→ 比例式の性質
→ 比例式の性質
p.119 問2
\(\begin{split}{\small (1)}~x=12\end{split}\) \(\begin{split}{\small (2)}~x=\frac{\,48\,}{\,5\,}\end{split}\)
\(\begin{split}{\small (1)}~x=12\end{split}\) \(\begin{split}{\small (2)}~x=\frac{\,48\,}{\,5\,}\end{split}\)
■ 同じタイプの問題の解説
→ 比例式の性質
→ 比例式の性質
p.119 問3\(\begin{split}{\small (1)}~\end{split}\)外側の2数の積は \(12{\, \small \times \,}3=36\)
内側の2数の積は \(9{\, \small \times \,}4=36\)
これより、等しい
\(\begin{split}{\small (2)}~\end{split}\)外側の2数の積は \(8{\, \small \times \,}6=48\)
内側の2数の積は \(\begin{split}5{\, \small \times \,}\frac{\,48\,}{\,5\,}=48\end{split}\)
これより、等しい
内側の2数の積は \(9{\, \small \times \,}4=36\)
これより、等しい
\(\begin{split}{\small (2)}~\end{split}\)外側の2数の積は \(8{\, \small \times \,}6=48\)
内側の2数の積は \(\begin{split}5{\, \small \times \,}\frac{\,48\,}{\,5\,}=48\end{split}\)
これより、等しい
■ 同じタイプの問題の解説
→ 比例式の性質
→ 比例式の性質
p.120 問4
\(\begin{split}{\small (1)}~x=15\end{split}\) \(\begin{split}{\small (2)}~x=\frac{\,7\,}{\,2\,}\end{split}\)
\(\begin{split}{\small (3)}~x=\frac{\,3\,}{\,2\,}\end{split}\) \(\begin{split}{\small (4)}~x=12\end{split}\)
\(\begin{split}{\small (1)}~x=15\end{split}\) \(\begin{split}{\small (2)}~x=\frac{\,7\,}{\,2\,}\end{split}\)
\(\begin{split}{\small (3)}~x=\frac{\,3\,}{\,2\,}\end{split}\) \(\begin{split}{\small (4)}~x=12\end{split}\)
■ 同じタイプの問題の解説
→ 比例式の性質
→ 比例式の性質
p.120 問5 \(150~{\rm mL}\)
■ 同じタイプの問題の解説
→ 比例式の性質
→ 比例式の性質
p.121 問6 約 \(6.7~{\rm m}\)
■ 同じタイプの問題の解説
→ 比例式の性質
→ 比例式の性質
p.121 問7 \(4~{\rm km}\)
■ 同じタイプの問題の解説
→ 比例式の性質
→ 比例式の性質
確かめよう
p.121 確かめよう 2 生徒 \(12\) 人、折り紙 \(32\) 枚
■ 同じタイプの問題の解説
→ 1次方程式と過不足
→ 1次方程式と過不足
p.121 確かめよう 4 約 \(88.9~{\rm cm}\)
■ 同じタイプの問題の解説
→ 比例式の性質
→ 比例式の性質
次のページ「4章 比例と反比例」


